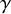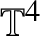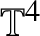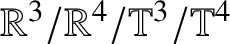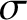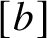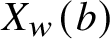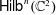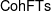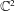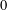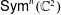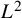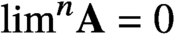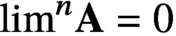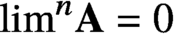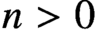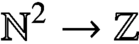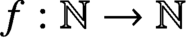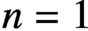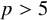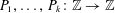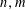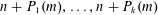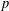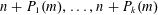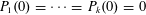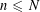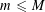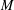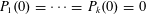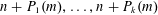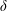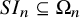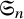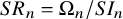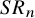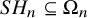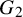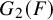Most cited
This page lists all time most cited articles for this title. Please use the publication date filters on the left if you would like to restrict this list to recently published content, for example to articles published in the last three years. The number of times each article was cited is displayed to the right of its title and can be clicked to access a list of all titles this article has been cited by.
- Cited by 7
Sharp smoothing properties of averages over curves
- Part of:
-
- Published online by Cambridge University Press:
- 10 February 2023, e4
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
- Cited by 7
Unconditional uniqueness for the energy-critical nonlinear Schrödinger equation on
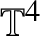 $\mathbb {T}^{4}$
$\mathbb {T}^{4}$
- Part of:
-
- Published online by Cambridge University Press:
- 13 January 2022, e3
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
- Cited by 7
Cordial elements and dimensions of affine Deligne–Lusztig varieties
- Part of:
-
- Published online by Cambridge University Press:
- 08 September 2021, e9
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
- Cited by 7
IGUSA’S CONJECTURE FOR EXPONENTIAL SUMS: OPTIMAL ESTIMATES FOR NONRATIONAL SINGULARITIES
- Part of:
-
- Published online by Cambridge University Press:
- 31 July 2019, e3
-
- Article
-
- You have access
- Open access
- Export citation
- Cited by 7
HIGHER GENUS GROMOV–WITTEN THEORY OF
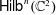 $\mathsf{Hilb}^{n}(\mathbb{C}^{2})$ AND
$\mathsf{Hilb}^{n}(\mathbb{C}^{2})$ AND 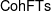 $\mathsf{CohFTs}$ ASSOCIATED TO LOCAL CURVES
$\mathsf{CohFTs}$ ASSOCIATED TO LOCAL CURVES
- Part of:
-
- Published online by Cambridge University Press:
- 31 July 2019, e4
-
- Article
-
- You have access
- Open access
- Export citation
- Cited by 6
THE CONORMAL TORUS IS A COMPLETE KNOT INVARIANT
- Part of:
-
- Published online by Cambridge University Press:
- 06 September 2019, e6
-
- Article
-
- You have access
- Open access
- Export citation
- Cited by 6
Global solutions for 1D cubic defocusing dispersive equations: Part I
- Part of:
-
- Published online by Cambridge University Press:
- 04 December 2023, e31
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
- Cited by 6
Smooth imploding solutions for 3D compressible fluids
- Part of:
-
- Published online by Cambridge University Press:
- 12 February 2025, e6
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
- Cited by 6
Simultaneously vanishing higher derived limits
- Part of:
-
- Published online by Cambridge University Press:
- 14 June 2021, e4
-
- Article
-
- You have access
- Open access
- Export citation
- Cited by 6
Local newforms for the general linear groups over a non-archimedean local field
- Part of:
-
- Published online by Cambridge University Press:
- 13 December 2022, e24
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
- Cited by 6
On the relative minimal model program for fourfolds in positive and mixed characteristic
-
- Published online by Cambridge University Press:
- 24 March 2023, e10
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
- Cited by 6
Resolutions of toric subvarieties by line bundles and applications
- Part of:
-
- Published online by Cambridge University Press:
- 27 November 2024, e24
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
- Cited by 6
Quantitative Heegaard Floer cohomology and the Calabi invariant
- Part of:
-
- Published online by Cambridge University Press:
- 21 December 2022, e27
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
- Cited by 5
Proof of a conjecture of Galvin
- Part of:
-
- Published online by Cambridge University Press:
- 21 December 2020, e15
-
- Article
-
- You have access
- Open access
- Export citation
- Cited by 5
POLYNOMIAL PATTERNS IN THE PRIMES
- Part of:
-
- Published online by Cambridge University Press:
- 12 February 2018, e1
-
- Article
-
- You have access
- Open access
- Export citation
- Cited by 5
The Hilbert series of the superspace coinvariant ring
- Part of:
-
- Published online by Cambridge University Press:
- 17 October 2024, e16
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
- Cited by 5
On genus one mirror symmetry in higher dimensions and the BCOV conjectures
- Part of:
-
- Published online by Cambridge University Press:
- 31 August 2022, e19
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
- Cited by 5
Logarithmic Donaldson–Thomas theory
- Part of:
-
- Published online by Cambridge University Press:
- 18 April 2024, e9
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
- Cited by 5
On Thakur’s basis conjecture for multiple zeta values in positive characteristic
- Part of:
-
- Published online by Cambridge University Press:
- 12 October 2023, e26
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
- Cited by 5
The Local Langlands Conjecture for
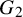 $G_2$
$G_2$
- Part of:
-
- Published online by Cambridge University Press:
- 19 October 2023, e28
-
- Article
-
- You have access
- Open access
- HTML
- Export citation