Hostname: page-component-7dd5485656-tbj44 Total loading time: 0 Render date: 2025-10-31T19:12:40.723Z Has data issue: false hasContentIssue false
  • English
  • Français

Simultaneously vanishing higher derived limits

Part of: Abelian categories Homology and cohomology theories Set theory

Published online by Cambridge University Press:  14 June 2021

Jeffrey Bergfalk  and
Chris Lambie-Hanson Open the ORCID record for Chris Lambie-Hanson [Opens in a new window]
Jeffrey Bergfalk
Affiliation:
Universität Wien, Institut für Mathematik, Kurt Gödel Research Center, Kolingasse 14-16, 1010 Wien, Austria;. Centro de Ciencas Matemáticas, UNAM, A.P. 61-3, Xangari, Morelia, Michoacán, 58089, México; E-mail: jeffrey.bergfalk@univie.ac.at.
Chris Lambie-Hanson
Affiliation:
Department of Mathematics and Applied Mathematics, Virginia Commonwealth University, Richmond, VA 23284, USA; E-mail: cblambiehanso@vcu.edu.

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In 1988, Sibe Mardešić and Andrei Prasolov isolated an inverse system 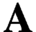$\textbf {A}$ with the property that the additivity of strong homology on any class of spaces which includes the closed subsets of Euclidean space would entail that 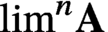$\lim ^n\textbf {A}$ (the nth derived limit of 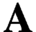$\textbf {A}$) vanishes for every 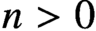$n>0$. Since that time, the question of whether it is consistent with the $\mathsf {ZFC}$ axioms that 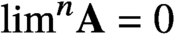$\lim ^n \textbf {A}=0$ for every 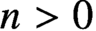$n>0$ has remained open. It remains possible as well that this condition in fact implies that strong homology is additive on the category of metric spaces.

We show that assuming the existence of a weakly compact cardinal, it is indeed consistent with the $\mathsf {ZFC}$ axioms that 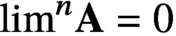$\lim ^n \textbf {A}=0$ for all 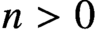$n>0$. We show this via a finite-support iteration of Hechler forcings which is of weakly compact length. More precisely, we show that in any forcing extension by this iteration, a condition equivalent to 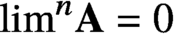$\lim ^n\textbf {A}=0$ will hold for each 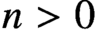$n>0$. This condition is of interest in its own right; namely, it is the triviality of every coherent n-dimensional family of certain specified sorts of partial functions 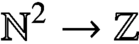$\mathbb {N}^2\to \mathbb {Z}$ which are indexed in turn by n-tuples of functions 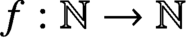$f:\mathbb {N}\to \mathbb {N}$. The triviality and coherence in question here generalise the classical and well-studied case of 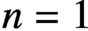$n=1$.

MSC classification

Primary: 03E05: Other combinatorial set theory
Secondary: 03E75: Applications of set theory 03E55: Large cardinals 55N07: Steenrod-Sitnikov homologies 55N40: Axioms for homology theory and uniqueness theorems 18E25: Derived functors and satellites

Information

Type
Foundations
Information
Forum of Mathematics, Pi , Volume 9 , 2021 , e4
Check for updates
Creative Commons
Creative Common License - CCCreative Common License - BY
This is an Open Access article, distributed under the terms of the Creative Commons Attribution licence (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted re-use, distribution, and reproduction in any medium, provided the original work is properly cited.
Copyright
© The Author(s), 2021. Published by Cambridge University Press.

References

Bannister, N., Bergfalk, J. and Moore, J. T, ‘On the additivity of strong homology for locally compact separable metric spaces’, Preprint, 2020, arXiv:2008.13089.Google Scholar
Barratt, M. G. and Milnor, J., ‘An example of anomalous singular homology’, Proc. Amer. Math. Soc. 13 (1962), 293–297.CrossRefGoogle Scholar
Baumgartner, J. E., ‘Iterated forcing’, in Surveys in Set Theory, London Mathematical Society Lecture Note Series, vol. 87 (Cambridge University Press, Cambridge, 1983), 1–59.Google Scholar
Bergfalk, J., ‘Strong homology, derived limits, and set theory’, Fund. Math. 236(1) (2017), 71–82.CrossRefGoogle Scholar
Bergfalk, J., Hrušák, M. and Lambie-Hanson, C., ‘Simultaneously vanishing higher derived limits without large cardinals’, Preprint, 2021, arXiv:2102.06699.Google Scholar
Bergfalk, J., Hrušák, M. and Shelah, S., ‘Ramsey theory for highly connected monochromatic subgraphs’, Acta Math. Hungar. 163(1) (2021), 309–322.CrossRefGoogle Scholar
Bergfalk, J. and Lambie-Hanson, C., ‘The cohomology of the ordinals I: Basic theory and consistency results’, Preprint, 2019, arXiv:1902.02736.Google Scholar
Clausen, D. and Scholze, P., Personal communication, July 2019.Google Scholar
Dow, A., Simon, P. and Vaughan, J. E., ‘Strong homology and the proper forcing axiom’, Proc. Amer. Math. Soc. 106(3) (1989), 821–828.CrossRefGoogle Scholar
Eda, K. and Kawamura, K., ‘The singular homology of the Hawaiian earring’, J. Lond. Math. Soc. (2) 62(1) (2000), 305–310.CrossRefGoogle Scholar
Eklof, P. C. and Mekler, A. H., Almost Free Modules, revised edn, North-Holland Mathematical Library, vol. 65 (North-Holland Publishing Co., Amsterdam, 2002).Google Scholar
Farah, I., ‘A coherent family of partial functions on $\textbf{N}$ ’, Proc. Amer. Math. Soc. 124(9) (1996), 2845–2852.CrossRefGoogle Scholar
Goblot, R., ‘Sur les dérivés de certaines limites projectives. Applications aux modules’, Bull. Sci. Math. (2) 94 (1970), 251–255.Google Scholar
Günther, B., ‘The Vietoris system in strong shape and strong homology’, Fund. Math. 141(2) (1992), 147–168.CrossRefGoogle Scholar
Jensen, C. U., Les foncteurs dérivés de $\underleftarrow{\lim}$ et leurs applications en théorie des modules, Lecture Notes in Mathematics, vol. 254 ( Springer-Verlag, Berlin-New York, 1972).CrossRefGoogle Scholar
Kamo, S., ‘Almost coinciding families and gaps in $P\left(\omega \right)$ ’, J. Math. Soc. Japan 45(2) (1993), 357–368.CrossRefGoogle Scholar
Kanamori, A., The Higher Infinite, second edn, Springer Monographs in Mathematics (Springer-Verlag, Berlin, 2003). Large cardinals in set theory from their beginnings. Google Scholar
Kunen, K., Set Theory, Studies in Logic and the Foundations of Mathematics, vol. 102 (North-Holland Publishing Co., Amsterdam-New York, 1980). An introduction to independence proofs. Google Scholar
Lambie-Hanson, C., ‘Disjoint type graphs with no short odd cycles’, unpublished note, 2019, arXiv:2004.04189.Google Scholar
Lisica, J. T., ‘Strong bonding homology and cohomology’, Topology Appl. 153(2-3) (2005), 394–447.CrossRefGoogle Scholar
Mardešić, S., Strong Shape and Homology, Springer Monographs in Mathematics ( Springer-Verlag, Berlin, 2000).CrossRefGoogle Scholar
Mardešić, S. and Prasolov, A. V., ‘Strong homology is not additive’, Trans. Amer. Math. Soc. 307(2) (1988), 725–744.CrossRefGoogle Scholar
Milnor, J., ‘On axiomatic homology theory’, Pacific J. Math. 12 (1962), 337–341.CrossRefGoogle Scholar
Milnor, J., ‘On the Steenrod homology theory’, in Novikov Conjectures, Index Theorems and Rigidity, Vol. 1 (Oberwolfach, 1993), London Mathematical Society Lecture Notes Series, vol. 226 (Cambridge University Press, Cambridge, 1995), 79–96.CrossRefGoogle Scholar
Moore, J. T., ‘The proper forcing axiom’, in Proceedings of the International Congress of Mathematicians. Volume II (Hindustan Book Agency, New Delhi, 2010), 3–29.Google Scholar
Osofsky, B. L., ‘The subscript of ${\aleph}_n$ , projective dimension, and the vanishing of ${\underleftarrow{\lim}}^{(n)}$ ’, Bull. Amer. Math. Soc. 80 (1974), 8–26.CrossRefGoogle Scholar
Prasolov, A. V. ‘Non-additivity of strong homology’, Topology Appl. 153(2-3) (2005), 493–527.CrossRefGoogle Scholar
Scholze, P., ‘Lectures on condensed mathematics’, unpublished lecture notes (2019). URL: https://www.math.uni-bonn.de/people/scholze/Condensed.pdf. Google Scholar
Serre, J.-P., ‘Faisceaux algébriques cohérents’, Ann. of Math. (2) 61 (1955), 197–278.CrossRefGoogle Scholar
Shelah, S., ‘Infinite abelian groups, Whitehead problem and some constructions’, Israel J. Math. 18 (1974), 243–256.CrossRefGoogle Scholar
Todorcevic, S., ‘Directed sets and cofinal types’, Trans. Amer. Math. Soc. 290(2) (1985), 711–723.CrossRefGoogle Scholar
Todorcevic, S., ‘Reals and positive partition relations’, in Logic, Methodology and Philosophy of Science, VII (Salzburg, 1983), Studies in Logic and the Foundations of Mathematics, vol. 114 (North-Holland, Amsterdam, 1986), 159–169.CrossRefGoogle Scholar
Todorcevic, S., Partition Problems in Topology, Contemporary Mathematics, vol. 84 (American Mathematical Society, Providence, RI, 1989).CrossRefGoogle Scholar
Todorcevic, S. ‘The first derived limit and compactly ${F}_{\sigma }$ sets’, J. Math. Soc. Japan 50(4) (1998), 831–836.CrossRefGoogle Scholar
Veličković, B. and Vignati, A., In preparation.Google Scholar
Weibel, C. A., An Introduction to Homological Algebra, Cambridge Studies in Advanced Mathematics, vol. 38 (Cambridge University Press, Cambridge, 1994).CrossRefGoogle Scholar