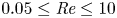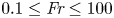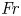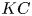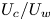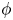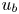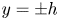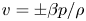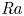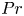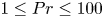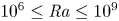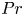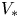Open access
Contents
JFM Papers
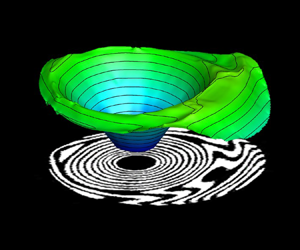
Scale-space energy density for inhomogeneous turbulence based on filtered velocities
-
- Published online by Cambridge University Press:
- 01 December 2021, A34
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Asymptotics of streamwise Reynolds stress in wall turbulence
-
- Published online by Cambridge University Press:
- 29 November 2021, A18
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
JFM Rapids
On state instability of the bi-stable flow past a notchback bluff body
-
- Published online by Cambridge University Press:
- 29 November 2021, R6
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
JFM Papers
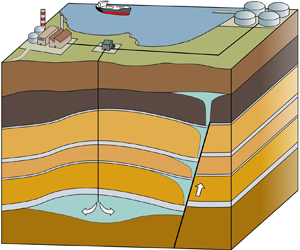
Leakage dynamics of fault zones: experimental and analytical study with application to CO2 storage
-
- Published online by Cambridge University Press:
- 29 November 2021, A31
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Turbulent flow in curved channels
-
- Published online by Cambridge University Press:
- 26 November 2021, A21
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Transition in an infinite swept-wing boundary layer subject to surface roughness and free-stream turbulence
-
- Published online by Cambridge University Press:
- 26 November 2021, A24
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Magnetoconvection in a horizontal duct flow at very high Hartmann and Grashof numbers
-
- Published online by Cambridge University Press:
- 26 November 2021, A29
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
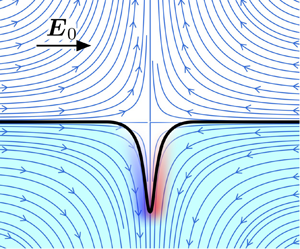
Instability of a planar fluid interface under a tangential electric field in a stagnation point flow
-
- Published online by Cambridge University Press:
- 26 November 2021, A25
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Microlayer dynamics during the growth process of a single vapour bubble under subcooled flow boiling conditions
-
- Published online by Cambridge University Press:
- 26 November 2021, A23
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Settling of highly porous and impermeable particles in linear stratification: implications for marine aggregates
-
- Published online by Cambridge University Press:
- 23 November 2021, A9
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Boundary layer dynamics and bottom friction in combined wave–current flows over large roughness elements
-
- Published online by Cambridge University Press:
- 23 November 2021, A11
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Modulation of fluid temperature fluctuations by particles in turbulence
-
- Published online by Cambridge University Press:
- 22 November 2021, A6
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Flow interaction of three-dimensional self-propelled flexible plates in tandem
-
- Published online by Cambridge University Press:
- 22 November 2021, A5
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Erratum
Numerical experiments on turbulent entrainment and mixing of scalars – ERRATUM
-
- Published online by Cambridge University Press:
- 19 November 2021, E1
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
JFM Papers
Dispersion in doublet-type flows through highly anisotropic porous formations
-
- Published online by Cambridge University Press:
- 18 November 2021, A2
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
JFM Rapids
The ultimate state of turbulent permeable-channel flow
-
- Published online by Cambridge University Press:
- 18 November 2021, R3
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
JFM Papers
Rheotaxis and migration of an unsteady microswimmer
-
- Published online by Cambridge University Press:
- 17 November 2021, A30
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Bounds for rotating Rayleigh–Bénard convection at large Prandtl number
-
- Published online by Cambridge University Press:
- 17 November 2021, A33
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Boundary layers in turbulent vertical convection at high Prandtl number
-
- Published online by Cambridge University Press:
- 16 November 2021, A32
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
JFM Rapids
Colliding respiratory jets as a mechanism of air exchange and pathogen transport during conversations
-
- Published online by Cambridge University Press:
- 16 November 2021, R1
-
- Article
-
- You have access
- Open access
- HTML
- Export citation