Contents
Front Cover (OFC, IFC) and matter
CPC volume 21 issue 5 Cover and Front matter
-
- Published online by Cambridge University Press:
- 26 July 2012, pp. f1-f2
-
- Article
-
- You have access
- Export citation
Paper
Dense Graphs With a Large Triangle Cover Have a Large Triangle Packing
-
- Published online by Cambridge University Press:
- 27 September 2012, pp. 952-962
-
- Article
- Export citation
On the Maximum Number of Edges in a Triple System Not Containing a Disjoint Family of a Given Size
-
- Published online by Cambridge University Press:
- 02 February 2012, pp. 141-148
-
- Article
- Export citation
Conflict-Free Colourings of Uniform Hypergraphs With Few Edges
-
- Published online by Cambridge University Press:
- 20 April 2012, pp. 611-622
-
- Article
- Export citation
Front Cover (OFC, IFC) and matter
CPC volume 21 issue 3 Cover and Front matter
-
- Published online by Cambridge University Press:
- 12 April 2012, pp. f1-f2
-
- Article
-
- You have access
- Export citation
Paper
A Pair of Forbidden Subgraphs and 2-Factors
-
- Published online by Cambridge University Press:
- 02 February 2012, pp. 149-158
-
- Article
- Export citation
On the Banach-Space-Valued Azuma Inequality and Small-Set Isoperimetry of Alon–Roichman Graphs
-
- Published online by Cambridge University Press:
- 18 January 2012, pp. 623-634
-
- Article
- Export citation
Back Cover (IBC, OBC) and matter
CPC volume 21 issue 5 Cover and Back matter
-
- Published online by Cambridge University Press:
- 26 July 2012, pp. b1-b3
-
- Article
-
- You have access
- Export citation
Front Cover (OFC, IFC) and matter
CPC volume 21 issue 6 Cover and Front matter
-
- Published online by Cambridge University Press:
- 27 September 2012, pp. f1-f2
-
- Article
-
- You have access
- Export citation
Back Cover (IBC, OBC) and matter
CPC volume 21 issue 3 Cover and Back matter
-
- Published online by Cambridge University Press:
- 12 April 2012, pp. b1-b2
-
- Article
-
- You have access
- Export citation
Paper
2-Cancellative Hypergraphs and Codes
-
- Published online by Cambridge University Press:
- 02 February 2012, pp. 159-177
-
- Article
- Export citation
Back Cover (IBC, OBC) and matter
CPC volume 21 issue 6 Cover and Back matter
-
- Published online by Cambridge University Press:
- 27 September 2012, pp. b1-b2
-
- Article
-
- You have access
- Export citation
Paper
Approximating Cayley Diagrams Versus Cayley Graphs
-
- Published online by Cambridge University Press:
- 04 January 2012, pp. 635-641
-
- Article
- Export citation
Star Versus Two Stripes Ramsey Numbers and a Conjecture of Schelp
-
- Published online by Cambridge University Press:
- 02 February 2012, pp. 179-186
-
- Article
- Export citation
Front Cover (OFC, IFC) and matter
CPC volume 21 issue 4 Cover and Front matter
-
- Published online by Cambridge University Press:
- 07 June 2012, pp. f1-f2
-
- Article
-
- You have access
- Export citation
Paper
The Maximum Number of Triangles in C2k+1-Free Graphs
-
- Published online by Cambridge University Press:
- 02 February 2012, pp. 187-191
-
- Article
- Export citation
Back Cover (IBC, OBC) and matter
CPC volume 21 issue 4 Cover and Back matter
-
- Published online by Cambridge University Press:
- 07 June 2012, pp. b1-b3
-
- Article
-
- You have access
- Export citation
Paper
Hypergraphs with No Cycle of a Given Length
-
- Published online by Cambridge University Press:
- 02 February 2012, pp. 193-201
-
- Article
- Export citation
Edge Colourings of Graphs Avoiding Monochromatic Matchings of a Given Size
-
- Published online by Cambridge University Press:
- 02 February 2012, pp. 203-218
-
- Article
- Export citation
Most Probably Intersecting Families of Subsets
-
- Published online by Cambridge University Press:
- 02 February 2012, pp. 219-227
-
- Article
- Export citation
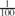
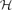
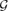
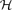
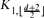 -free graph of minimum degree at least
-free graph of minimum degree at least 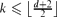 every connected graph
every connected graph 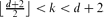 , and prove that only a finite number of connected graphs
, and prove that only a finite number of connected graphs 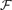
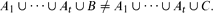
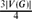 , then in every 2-colouring of the edges of
, then in every 2-colouring of the edges of 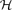
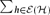

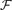
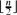 -element subsets. We determine the most probably inclusion-free family too, when the number of members is
-element subsets. We determine the most probably inclusion-free family too, when the number of members is 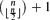 .
.