Contents
Paper
Are Stable Instances Easy?
-
- Published online by Cambridge University Press:
- 26 July 2012, pp. 643-660
-
- Article
- Export citation
Detachments of Hypergraphs I: The Berge–Johnson Problem
-
- Published online by Cambridge University Press:
- 27 February 2012, pp. 483-495
-
- Article
- Export citation
Connectivity for Bridge-Addable Monotone Graph Classes
-
- Published online by Cambridge University Press:
- 30 July 2012, pp. 803-815
-
- Article
- Export citation
Introduction
My Friend and Colleague, Richard Schelp
-
- Published online by Cambridge University Press:
- 02 February 2012, pp. 1-9
-
- Article
- Export citation
Paper
Asymptotic Improvements to the Lower Bound of Certain Bipartite Turán Numbers
-
- Published online by Cambridge University Press:
- 03 October 2011, pp. 323-329
-
- Article
- Export citation
Critical Probabilities of 1-Independent Percolation Models
-
- Published online by Cambridge University Press:
- 02 February 2012, pp. 11-22
-
- Article
- Export citation
Perfect Graphs of Fixed Density: Counting and Homogeneous Sets
-
- Published online by Cambridge University Press:
- 14 May 2012, pp. 661-682
-
- Article
- Export citation
Cops and Robbers on Geometric Graphs
-
- Published online by Cambridge University Press:
- 16 August 2012, pp. 816-834
-
- Article
- Export citation
Order-Invariant Measures on Fixed Causal Sets
-
- Published online by Cambridge University Press:
- 19 January 2012, pp. 330-357
-
- Article
- Export citation
Set Families With a Forbidden Induced Subposet
-
- Published online by Cambridge University Press:
- 22 March 2012, pp. 496-511
-
- Article
- Export citation
Testing Odd-Cycle-Freeness in Boolean Functions
-
- Published online by Cambridge University Press:
- 10 August 2012, pp. 835-855
-
- Article
- Export citation
Corrádi and Hajnal's Theorem for Sparse Random Graphs
-
- Published online by Cambridge University Press:
- 02 February 2012, pp. 23-55
-
- Article
- Export citation
Scott's Induced Subdivision Conjecture for Maximal Triangle-Free Graphs
-
- Published online by Cambridge University Press:
- 21 March 2012, pp. 512-514
-
- Article
- Export citation
Space Crossing Numbers
-
- Published online by Cambridge University Press:
- 16 March 2012, pp. 358-373
-
- Article
- Export citation
Strong Convergence of Partial Match Queries in Random Quadtrees
-
- Published online by Cambridge University Press:
- 27 April 2012, pp. 683-694
-
- Article
- Export citation
A Graph Polynomial for Independent Sets of Bipartite Graphs
-
- Published online by Cambridge University Press:
- 10 July 2012, pp. 695-714
-
- Article
- Export citation
Some Properties of Lower Level-Sets of Convolutions
-
- Published online by Cambridge University Press:
- 12 April 2012, pp. 515-530
-
- Article
- Export citation
Measurable Events Indexed by Trees
-
- Published online by Cambridge University Press:
- 12 March 2012, pp. 374-411
-
- Article
- Export citation
Longest Path Distance in Random Circuits
-
- Published online by Cambridge University Press:
- 03 July 2012, pp. 856-881
-
- Article
- Export citation
Monochromatic Cycles in 2-Coloured Graphs
-
- Published online by Cambridge University Press:
- 19 March 2012, pp. 57-87
-
- Article
- Export citation
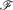
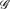
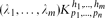 be a hypergraph with vertex partition {
be a hypergraph with vertex partition {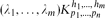 to be expressed as the union
to be expressed as the union 



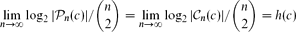
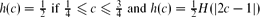
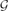
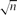
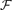
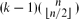 . This extends a result of Bukh [1], which in turn generalizes several known results including Sperner's theorem.
. This extends a result of Bukh [1], which in turn generalizes several known results including Sperner's theorem.