We prove new results about comparing the efficiency of general state space Markov chain Monte Carlo algorithms that randomly select a possibly different reversible method at each step (previously known only for finite state spaces). We also provide new, simpler, more accessible proofs of key results, and analyse numerous examples. We provide a full proof of the formula for the asymptotic variance for real-valued functionals on 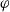$\varphi$-irreducible reversible Markov chains, first introduced by Kipnis and Varadhan (1986, Commun. Math. Phys. 104, 1–19). Given two Markov kernels P and Q with stationary measure 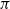$\pi$, we say that the Markov kernel P efficiency-dominates the Markov kernel Q if the asymptotic variance with respect to P is at most the asymptotic variance with respect to Q for every real-valued functional 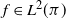$f\in L^2(\pi)$. Assuming only a basic background in functional analysis, we prove that for two reversible Markov kernels P and Q, P efficiency-dominates Q if and only if the operator 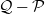$\mathcal{Q}-\mathcal{P}$, where 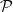$\mathcal{P}$ is the operator on 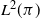$L^2(\pi)$ that maps 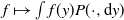$f\mapsto\int f(y)P(\cdot,\mathrm{d}y)$ and similarly for 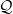$\mathcal{Q}$, is positive on 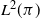$L^2(\pi)$, i.e. 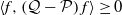$\langle f,\left(\mathcal{Q}-\mathcal{P}\right)f\rangle\geq0$ for every 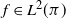$f\in L^2(\pi)$ (previous proofs for general state spaces use technical results from monotone operator function theory). We use this result to show that under mild conditions, sandwich variants of data augmentation algorithms efficiency-dominate the original algorithm. We also provide other easy-to-check sufficient conditions for efficiency dominance, some of which are generalized from the finite state space case. We also provide a proof based on that of Tierney (1998, Ann. Appl. Prob. 8, 1–9) that Peskun dominance is a sufficient condition for efficiency dominance for reversible kernels. Using these results, we show that Markov kernels formed by random selection of other ‘component’ Markov kernels will always efficiency-dominate another Markov kernel formed in this way, as long as the component kernels of the former efficiency-dominate those of the latter. These results on the efficiency dominance of combining component kernels generalizes the results on the efficiency dominance of combined chains introduced by Neal and Rosenthal (2024, J. Appl. Prob. 62, 188–208) from finite state spaces to general state spaces.

We study quasi-stationary distributions and quasi-limiting behaviour of Markov chains in general reducible state spaces with absorption. First, we consider state spaces that can be decomposed into two successive subsets (with communication possible in a single direction), differentiating between three situations, and characterize the exponential order of magnitude and the exact polynomial correction, called the polynomial convergence parameter, for the leading-order term of the semigroup for large time. Second, we consider general Markov chains with finitely or countably many communication classes by applying the first results iteratively over the communication classes of the chain. We conclude with an application of these results to the case of denumerable state spaces, where we prove existence for a quasi-stationary distribution without assuming irreducibility before absorption, but only aperiodicity, existence of a Lyapunov function, and existence of a point with almost surely finite return time.

In this paper we are concerned with susceptible–infected–removed (SIR) epidemics with vertex-dependent recovery and infection rates on complete graphs. We show that the hydrodynamic limit of our model is driven by a nonlinear function-valued ordinary differential equation consistent with a mean-field analysis. We further show that the fluctuation of our process is driven by a generalized Ornstein–Uhlenbeck process. A key step in the proofs of the main results is to show that states of different vertices are approximately independent as the population $N\rightarrow+\infty$.

Designing efficient and rigorous numerical methods for sequential decision-making under uncertainty is a difficult problem that arises in many applications frameworks. In this paper we focus on the numerical solution of a subclass of impulse control problems for the piecewise deterministic Markov process (PDMP) when the jump times are hidden. We first state the problem as a partially observed Markov decision process (POMDP) on a continuous state space and with controlled transition kernels corresponding to some specific skeleton chains of the PDMP. We then proceed to build a numerically tractable approximation of the POMDP by tailor-made discretizations of the state spaces. The main difficulty in evaluating the discretization error comes from the possible random jumps of the PDMP between consecutive epochs of the POMDP and requires special care. Finally, we discuss the practical construction of discretization grids and illustrate our method on simulations.

We study stationary distributions in the context of stochastic reaction networks. In particular, we are interested in complex balanced reaction networks and the reduction of such networks by assuming that a set of species (called non-interacting species) are degraded fast (and therefore essentially absent from the network), implying that some reaction rates are large relative to others. Technically, we assume that these reaction rates are scaled by a common parameter N and let $N\to\infty$. The limiting stationary distribution as $N\to\infty$ is compared with the stationary distribution of the reduced reaction network obtained by elimination of the non-interacting species. In general, the limiting stationary distribution could differ from the stationary distribution of the reduced reaction network. We identify various sufficient conditions under which these two distributions are the same, including when the reaction network is detailed balanced and when the set of non-interacting species consists of intermediate species. In the latter case, the limiting stationary distribution essentially retains the form of the complex balanced distribution. This finding is particularly surprising given that the reduced reaction network could be non-weakly reversible and might exhibit unconventional kinetics.

We study a continuous-time mutually catalytic branching model on the $\mathbb{Z}^{d}$. The model describes the behavior of two different populations of particles, performing random walk on the lattice in the presence of branching, that is, each particle dies at a certain rate and is replaced by a random number of offspring. The branching rate of a particle in one population is proportional to the number of particles of another population at the same site. We study the long time behavior for this model, in particular, coexistence and noncoexistence of two populations in the long run. Finally, we construct a sequence of renormalized processes and use duality techniques to investigate its limiting behavior.

The money exchange model is a type of agent-based model used to study how wealth distribution and inequality evolve through monetary exchanges between individuals. The primary focus of this model is to identify the limiting wealth distributions that emerge at the macroscopic level, given the microscopic rules governing the exchanges among agents. In this paper, we formulate generalized versions of the immediate exchange model, the uniform reshuffling model, and the uniform saving model, all of which are types of money exchange model, as discrete-time interacting particle systems and characterize their stationary distributions. Furthermore, we prove that, under appropriate scaling, the asymptotic wealth distribution converges to an exponential distribution for the uniform reshuffling model, and to either an exponential distribution or a gamma distribution depending on the tail behavior of the number of coins given/saved in the immediate exchange model and the random saving model, which generalizes the uniform saving model. In particular, our results provide a mathematically rigorous formulation and generalization of the assertions previously predicted in studies based on numerical simulations and heuristic arguments.

This paper investigates a continuous-time multidimensional risk model with stochastic returns driven by a geometric Lévy process, where each main claim is accompanied by a random number of delayed claims. By employing a framework of multivariate regular variation for claim sizes and allowing for arbitrarily dependent claim-number processes, we conduct asymptotic analyses for two types of ruin probabilities. Numerical examples are used to demonstrate the accuracy of our asymptotic estimates.

We study Langevin-type algorithms for sampling from Gibbs distributions such that the potentials are dissipative and their weak gradients have finite moduli of continuity not necessarily convergent to zero. Our main result is a non-asymptotic upper bound on the 2-Wasserstein distance between a Gibbs distribution and the law of general Langevin-type algorithms based on a Liptser–Shiryaev-type condition for change of measures and Poincaré inequalities. We apply this bound to show that the Langevin Monte Carlo algorithm can approximate Gibbs distributions with arbitrary accuracy if the potentials are dissipative and their gradients are uniformly continuous. We also propose Langevin-type algorithms with spherical smoothing for distributions whose potentials are not convex or continuously differentiable and show their polynomial complexities.

In this paper, we consider a bidimensional risk model with stochastic returns and dependent subexponential claims, in which every main claim may be accompanied by a delayed claim, occurring after an uncertain period of time. The surplus of each business line is allowed to be invested in a portfolio of risk-free assets, and the price process of the investment is modeled by a geometric Lévy process. Meanwhile, we employ a time-claim-dependent structure to describe the dependence among claims and the interarrival times. Some uniform asymptotic formulas for the finite-time ruin probabilities are derived under this structure. Finally, a simulation study is conducted to evaluate the accuracy of the derived results.

We show that the Potts model on a graph can be approximated by a sequence of independent and identically distributed spins in terms of Wasserstein distance at high temperatures. We prove a similar result for the Curie–Weiss–Potts model on the complete graph, conditioned on being close enough to any of its equilibrium macrostates, in the low-temperature regime. Our proof technique is based on Stein’s method for comparing the stationary distributions of two Glauber dynamics with similar updates, one of which is rapid mixing and contracting on a subset of the state space. Along the way, we prove a new upper bound on the mixing time of the Glauber dynamics for the conditional measure of the Curie–Weiss–Potts model near an equilibrium macrostate.

We describe the asymptotic behaviour of large degrees in random hyperbolic graphs for all values of the curvature parameter $\alpha$. We prove that, with high probability, the node degrees satisfy the following ordering property: the ranking of the nodes by decreasing degree coincides with the ranking of the nodes by increasing distance to the centre, at least up to any constant rank. In the sparse regime $\alpha>\tfrac{1}{2}$, the rank at which these two rankings cease to coincide is $n^{1/(1+8\alpha)+o(1)}$. We also provide a quantitative description of the large degrees by proving the convergence in distribution of the normalised degree process towards a Poisson point process. In particular, this establishes the convergence in distribution of the normalised maximum degree of the graph. A transition occurs at $\alpha = \tfrac{1}{2}$, which corresponds to the connectivity threshold of the model. For $\alpha < \tfrac{1}{2}$, the maximum degree is of order $n - O(n^{\alpha + 1/2})$, whereas for $\alpha \geq \tfrac{1}{2}$, the maximum degree is of order $n^{1/(2\alpha)}$. In the $\alpha < \tfrac{1}{2}$ and $\alpha > \tfrac{1}{2}$ cases, the limit distribution of the maximum degree belongs to the class of extreme value distributions (Weibull for $\alpha < \tfrac{1}{2}$ and Fréchet for $\alpha > \tfrac{1}{2}$). This refines previous estimates on the maximum degree for $\alpha > \tfrac{1}{2}$ and extends the study of large degrees to the dense regime $\alpha \leq \tfrac{1}{2}$.

We derive the exact asymptotics of $\mathbb{P} {\{\sup\nolimits_{\boldsymbol{t}\in {\mathcal{A}}}X(\boldsymbol{t})>u \}} \textrm{ as}\ u\to\infty,$ for a centered Gaussian field $X({\boldsymbol{t}}),\ {\boldsymbol{t}}\in \mathcal{A}\subset\mathbb{R}^n$, $n>1$ with continuous sample paths almost surely, for which $\arg \max_{\boldsymbol{t}\in {\mathcal{A}}} {\mathrm{Var}}(X(\boldsymbol{t}))$ is a Jordan set with a finite and positive Lebesgue measure of dimension $k\le n$ and its dependence structure is not necessarily locally stationary. Our findings are applied to derive the asymptotics of tail probabilities related to performance tables and chi processes, particularly when the covariance structure is not locally stationary.

In this paper we study one-sided hypothesis testing under random sampling without replacement, which frequently appears in the cryptographic problem setting, including the verification of measurement-based quantum computation. Suppose that $n+1$ binary random variables $X_1,\ldots, X_{n+1}$ follow a permutation invariant distribution and n binary random variables $X_1,\ldots, X_{n}$ are observed. Then, we propose randomized tests with a randomization parameter for the expectation of the $(n+1)$th random variable $X_{n+1}$ under a given significance level $\delta>0$. Our randomized tests significantly improve the upper confidence limit over deterministic tests. Our problem setting commonly appears in machine learning in addition to cryptographic scenarios by considering adversarial examples. Such studies are essential for expanding the applicable area of statistics. Although this paper addresses only binary random variables, a similar significant improvement by randomized tests can be expected for general non-binary random variables.

In this paper we consider a dynamic Erdős–Rényi graph in which edges, according to an alternating renewal process, change from present to absent and vice versa. The objective is to estimate the on- and off-time distributions while only observing the aggregate number of edges. This inverse problem is dealt with, in a parametric context, by setting up an estimator based on the method of moments. We provide conditions under which the estimator is asymptotically normal, and we point out how the corresponding covariance matrix can be identified. We also demonstrate how to adapt the estimation procedure if alternative subgraph counts are observed, such as the number of wedges or triangles.

We prove that for every locally stable and tempered pair potential $\phi$ with bounded range, there exists a unique infinite-volume Gibbs point process on $\mathbb{R}^{d}$ for every activity $\lambda < ({e}^{L} \hat{C}_{\phi})^{-1}$, where L is the local stability constant and $\hat{C}_{\phi} \,:\!=\, \sup_{x \in \mathbb{R}^{d}} \int_{\mathbb{R}^{d}} 1 - {e}^{-\left\lvert \phi(x, y) \right\rvert} \mathrm{d} y$ is the (weak) temperedness constant. Our result extends the uniqueness regime that is given by the classical Ruelle–Penrose bound by a factor of at least ${e}$, where the improvements become larger as the negative parts of the potential become more prominent (i.e. for attractive interactions at low temperature). Our technique is based on the approach of Dyer et al. (2004 Random Structures & Algorithms 24, 461–479): We show that for any bounded region and any boundary condition, we can construct a Markov process (in our case spatial birth–death dynamics) that converges rapidly to the finite-volume Gibbs point process while the effects of the boundary condition propagate sufficiently slowly. As a result, we obtain a spatial mixing property that implies uniqueness of the infinite-volume Gibbs measure.

A non-uniqueness phase for infinite clusters is proven for a class of marked random connection models (RCMs) on the d-dimensional hyperbolic space, ${\mathbb{H}^d}$, in a high volume-scaling regime. The approach taken in this paper utilizes the spherical transform on ${\mathbb{H}^d}$ to diagonalize convolution by the adjacency function and the two-point function and bound their $L^2\to L^2$ operator norms. Under some circumstances, this spherical transform approach also provides bounds on the triangle diagram that allows for a derivation of certain mean-field critical exponents. In particular, the results are applied to some Boolean and weight-dependent hyperbolic RCMs. While most of the paper is concerned with the high volume-scaling regime, the existence of the non-uniqueness phase is also proven without this scaling for some RCMs whose resulting graphs are almost surely not locally finite.