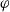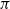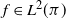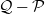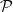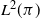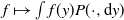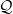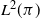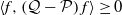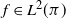1. Introduction
A common problem in statistics and other areas is that of estimating the average value of a function
![]() $f\,:\,\mathbf{X}\to\mathbf{R}$
with respect to a probability measure
$f\,:\,\mathbf{X}\to\mathbf{R}$
with respect to a probability measure
![]() $\pi$
. The domain of f,
$\pi$
. The domain of f,
![]() $\mathbf{X}$
, is called the state space. When the probability measure
$\mathbf{X}$
, is called the state space. When the probability measure
![]() $\pi$
is complicated and the expected value of f with respect to
$\pi$
is complicated and the expected value of f with respect to
![]() $\pi$
,
$\pi$
,
![]() $\mathbf{E}_{\pi}(f)$
, cannot be computed directly, Markov chain Monte Carlo (MCMC) algorithms are very effective; see [Reference Roberts and Rosenthal22]. In MCMC, the solution is to find a Markov chain
$\mathbf{E}_{\pi}(f)$
, cannot be computed directly, Markov chain Monte Carlo (MCMC) algorithms are very effective; see [Reference Roberts and Rosenthal22]. In MCMC, the solution is to find a Markov chain
![]() $\{X_k\}_{k\in\mathbf{N}}$
with underlying Markov kernel P, and estimate the expected value of f with respect to
$\{X_k\}_{k\in\mathbf{N}}$
with underlying Markov kernel P, and estimate the expected value of f with respect to
![]() $\pi$
as
$\pi$
as
 \begin{align*}\mathbf{E}_{\pi}(f)\approx\frac{1}{N}\sum_{k=1}^Nf(X_k)\,=\!:\,\overline{f}_{N}.\end{align*}
\begin{align*}\mathbf{E}_{\pi}(f)\approx\frac{1}{N}\sum_{k=1}^Nf(X_k)\,=\!:\,\overline{f}_{N}.\end{align*}
The advantage is that the Markov kernel P provides much simpler probability measures at each step, making it easier to compute, while the law of the Markov chain,
![]() $X_k$
, approaches the probability distribution
$X_k$
, approaches the probability distribution
![]() $\pi$
.
$\pi$
.
When the chosen function f is in
![]() $L^2(\pi)$
, i.e. when
$L^2(\pi)$
, i.e. when
![]() $\int_{\mathbf{X}}\left|\,f(x)\right|^2\pi(\mathrm{d}x)=\mathbf{E}_{\pi}(|f|^2)<\infty$
, one measure of the effectiveness of the chosen Markov kernel for the function f is the asymptotic variance of f using the kernel P, v (f, P), defined as
$\int_{\mathbf{X}}\left|\,f(x)\right|^2\pi(\mathrm{d}x)=\mathbf{E}_{\pi}(|f|^2)<\infty$
, one measure of the effectiveness of the chosen Markov kernel for the function f is the asymptotic variance of f using the kernel P, v (f, P), defined as
 \begin{align*}v(\,f,P)\,:\!=\,\lim_{N\to\infty}\left[N\,\mathbf{Var}\left(\frac{1}{N}\sum_{k=1}^Nf(X_k)\right)\right]=\lim_{N\to\infty}\left[\frac{1}{N}\mathbf{Var}\left(\sum_{k=1}^Nf(X_k)\right)\right]\!,\end{align*}
\begin{align*}v(\,f,P)\,:\!=\,\lim_{N\to\infty}\left[N\,\mathbf{Var}\left(\frac{1}{N}\sum_{k=1}^Nf(X_k)\right)\right]=\lim_{N\to\infty}\left[\frac{1}{N}\mathbf{Var}\left(\sum_{k=1}^Nf(X_k)\right)\right]\!,\end{align*}
where
![]() $\{X_k\}_{k\in\mathbf{N}}$
is a Markov chain with kernel P, started in stationarity (i.e.
$\{X_k\}_{k\in\mathbf{N}}$
is a Markov chain with kernel P, started in stationarity (i.e.
![]() $X_1\sim\pi$
).
$X_1\sim\pi$
).
Thus, if v( f, P) is finite, we would expect the variance of the estimate
![]() $\overline{f}_{N}$
to be near
$\overline{f}_{N}$
to be near
![]() $v(\,f,P)/N$
. Furthermore, if P is
$v(\,f,P)/N$
. Furthermore, if P is
![]() $\varphi$
-irreducible and reversible, a central limit theorem holds whenever v( f, P) is finite, and the variance of said central limit theorem is the asymptotic variance, i.e.
$\varphi$
-irreducible and reversible, a central limit theorem holds whenever v( f, P) is finite, and the variance of said central limit theorem is the asymptotic variance, i.e.
![]() $\sqrt{N}\left(\overline{f}_{N}-\mathbf{E}_{\pi}(f)\right)\overset{d}{\to}N(0,v(\,f,P))$
; see [Reference Kipnis and Varadhan15]. For further reference, see [Reference Geyer11, Reference Jones13, Reference Kipnis and Varadhan15, Reference Roberts and Rosenthal22, Reference Tierney26].
$\sqrt{N}\left(\overline{f}_{N}-\mathbf{E}_{\pi}(f)\right)\overset{d}{\to}N(0,v(\,f,P))$
; see [Reference Kipnis and Varadhan15]. For further reference, see [Reference Geyer11, Reference Jones13, Reference Kipnis and Varadhan15, Reference Roberts and Rosenthal22, Reference Tierney26].
![]() $X_1$
is not usually sampled from
$X_1$
is not usually sampled from
![]() $\pi$
directly, but if P is
$\pi$
directly, but if P is
![]() $\varphi$
-irreducible then we can get very close to sampling from
$\varphi$
-irreducible then we can get very close to sampling from
![]() $\pi$
directly by running the chain for a number of iterations before using the samples for estimation.
$\pi$
directly by running the chain for a number of iterations before using the samples for estimation.
In practice, it is common not to know in advance which function f will be needed, or need estimates for multiple functions. In these cases it is useful to have a Markov chain to run estimates for various functions simultaneously. Thus, we would like the variance of our estimates, and thus the asymptotic variance, to be as low as possible for not just one function
![]() $f\,:\,\mathbf{X}\to\mathbf{R}$
but for every function
$f\,:\,\mathbf{X}\to\mathbf{R}$
but for every function
![]() $f\,:\,\mathbf{X}\to\mathbf{R}$
simultaneously. This gives rise to the notion of an ordering of Markov kernels based on the asymptotic variance of functions in
$f\,:\,\mathbf{X}\to\mathbf{R}$
simultaneously. This gives rise to the notion of an ordering of Markov kernels based on the asymptotic variance of functions in
![]() $L^2(\pi)$
. Given two Markov kernels P and Q with stationary distribution
$L^2(\pi)$
. Given two Markov kernels P and Q with stationary distribution
![]() $\pi$
, we say that P efficiency-dominates Q if for every
$\pi$
, we say that P efficiency-dominates Q if for every
![]() $f\in L^2(\pi)$
,
$f\in L^2(\pi)$
,
![]() $v(\,f,P)\leq v(\,f,Q)$
.
$v(\,f,P)\leq v(\,f,Q)$
.
In this paper, we focus our attention on reversible Markov kernels. Many important algorithms, most notably the Metropolis–Hastings (MH) algorithm, are reversible; see [Reference Roberts and Rosenthal22, Reference Tierney27]. When the target probability density is difficult (or impossible) to calculate for the use of the MH algorithm, an exact approximation of the MH algorithm, an algorithm that uses the MH algorithm with an estimator of the target probability density, could be a viable option. In this case, it is possible this exact approximation algorithm run with one estimator efficiency-dominates the same algorithm run with a different estimator. See [Reference Andrieu and Vihola2] for more details.
Aside from the results in Section 5, many of the results in this paper are known but are scattered in the literature, have incomplete or unclear proofs, or are missing proofs altogether. We present new, clear, complete, and accessible proofs, using basic functional analysis where very technical results were previously used, most notably in the proof of Theorem 4.1. We show how once Theorem 4.1 is established, many further results are vastly simplified. This paper is self-contained, assuming knowledge of basic Markov chain theory and functional analysis.
1.1. Simple examples
We now present two simple examples, using the theory that will be developed in the rest of this paper, to provide some explicit examples of the material.
Example 1.1. As a simple example in finite state spaces, take
![]() $\mathbf{X}=\{1,2,3\}$
and
$\mathbf{X}=\{1,2,3\}$
and
![]() $\pi$
such that
$\pi$
such that
![]() $\pi(\{1\})=1/2$
,
$\pi(\{1\})=1/2$
,
![]() $\pi(\{2\})=1/4$
, and
$\pi(\{2\})=1/4$
, and
![]() $\pi(\{3\})=1/4$
. Then let P and Q be Markov kernels on
$\pi(\{3\})=1/4$
. Then let P and Q be Markov kernels on
![]() $\mathbf{X}$
such that
$\mathbf{X}$
such that
 \begin{equation*} \mathcal{P}\;=\;\begin{pmatrix} 0 &\quad \frac{1}{2} &\quad \frac{1}{2}\\[3pt] 1 &\quad 0 &\quad 0\\[3pt] 1 &\quad 0 &\quad 0\end{pmatrix} \qquad\text{and}\qquad \mathcal{Q}\;=\;\left(\frac{1}{3}\right)\begin{pmatrix} 1 &\quad 1 &\quad 1\\[3pt] 2 &\quad \frac{1}{2} &\quad \frac{1}{2}\\[3pt] 2 &\quad \frac{1}{2} &\quad \frac{1}{2}\end{pmatrix}. \end{equation*}
\begin{equation*} \mathcal{P}\;=\;\begin{pmatrix} 0 &\quad \frac{1}{2} &\quad \frac{1}{2}\\[3pt] 1 &\quad 0 &\quad 0\\[3pt] 1 &\quad 0 &\quad 0\end{pmatrix} \qquad\text{and}\qquad \mathcal{Q}\;=\;\left(\frac{1}{3}\right)\begin{pmatrix} 1 &\quad 1 &\quad 1\\[3pt] 2 &\quad \frac{1}{2} &\quad \frac{1}{2}\\[3pt] 2 &\quad \frac{1}{2} &\quad \frac{1}{2}\end{pmatrix}. \end{equation*}
Note that here we are using the expression for P as
 \begin{align*}\mathcal{P}=\begin{pmatrix} P(1,\{1\}) &\quad P(1,\{2\}) &\quad P(1,\{3\})\\[4pt] P(2,\{1\}) &\quad P(2,\{2\}) &\quad P(2,\{3\})\\[4pt] P(3,\{1\}) &\quad P(3,\{2\}) &\quad P(3,\{3\})\end{pmatrix},\end{align*}
\begin{align*}\mathcal{P}=\begin{pmatrix} P(1,\{1\}) &\quad P(1,\{2\}) &\quad P(1,\{3\})\\[4pt] P(2,\{1\}) &\quad P(2,\{2\}) &\quad P(2,\{3\})\\[4pt] P(3,\{1\}) &\quad P(3,\{2\}) &\quad P(3,\{3\})\end{pmatrix},\end{align*}
and similarly for Q.
To compare these two Markov kernels, it would be very difficult to calculate the asymptotic variance directly by definition. Even with the formula for the asymptotic variance from Theorem 3.1, which simplifies as
![]() $\mathbf{X}$
is finite to
$\mathbf{X}$
is finite to
![]() $v(\,f,P)=(a_2)^2\frac{1+\lambda_2}{1-\lambda_2}+(a_3)^2\frac{1+\lambda_3}{1-\lambda_3}$
for every
$v(\,f,P)=(a_2)^2\frac{1+\lambda_2}{1-\lambda_2}+(a_3)^2\frac{1+\lambda_3}{1-\lambda_3}$
for every
![]() $f\,:\,\mathbf{X}\to\mathbf{R}$
, where
$f\,:\,\mathbf{X}\to\mathbf{R}$
, where
![]() $\lambda_2$
and
$\lambda_2$
and
![]() $\lambda_3$
are eigenvalues of
$\lambda_3$
are eigenvalues of
![]() $\mathcal{Q}-\mathcal{P}$
, and
$\mathcal{Q}-\mathcal{P}$
, and
![]() $a_2$
and
$a_2$
and
![]() $a_3$
are the coefficients of the second and third eigenvectors of
$a_3$
are the coefficients of the second and third eigenvectors of
![]() $\mathcal{Q}-\mathcal{P}$
in the eigenvector representation of f (see Proposition 2 in [Reference Neal and Rosenthal20]), this is still a task that requires much computation.
$\mathcal{Q}-\mathcal{P}$
in the eigenvector representation of f (see Proposition 2 in [Reference Neal and Rosenthal20]), this is still a task that requires much computation.
However, by using Theorem 4.2, as
![]() $\mathbf{X}$
is finite we can simply calculate the eigenvalues of
$\mathbf{X}$
is finite we can simply calculate the eigenvalues of
![]() $\mathcal{Q}-\mathcal{P}$
, which are
$\mathcal{Q}-\mathcal{P}$
, which are
![]() $\{2/3,0,0\}$
, and as they are all non-negative, we can conclude that P efficiency-dominates Q.
$\{2/3,0,0\}$
, and as they are all non-negative, we can conclude that P efficiency-dominates Q.
Next we consider an example with a continuous state space.
Example 1.2. Suppose
![]() $\mathbf{X}=\mathbf{R}$
, and
$\mathbf{X}=\mathbf{R}$
, and
![]() $\pi\sim \mathrm{exponential}(1)$
, i.e.
$\pi\sim \mathrm{exponential}(1)$
, i.e.
![]() $\pi(\mathrm{d}y)=f(y)\mathrm{d}y$
, where
$\pi(\mathrm{d}y)=f(y)\mathrm{d}y$
, where
![]() $f\,:\,\mathbf{R}\to[0,\infty)$
such that
$f\,:\,\mathbf{R}\to[0,\infty)$
such that
![]() $f(y)=\mathrm{e}^{-y}$
if
$f(y)=\mathrm{e}^{-y}$
if
![]() $y\geq0$
and
$y\geq0$
and
![]() $f(y)=0$
if
$f(y)=0$
if
![]() $y<0$
.
$y<0$
.
Let
![]() $h\,:\,\mathbf{R}\to[0,\infty)$
be the density function of the
$h\,:\,\mathbf{R}\to[0,\infty)$
be the density function of the
![]() $\mathrm{normal}(0,1)$
distribution, i.e.
$\mathrm{normal}(0,1)$
distribution, i.e.
![]() $h(y)=\frac{1}{\sqrt{2\pi}}\mathrm{e}^{-\frac{y^2}{2}}$
for every
$h(y)=\frac{1}{\sqrt{2\pi}}\mathrm{e}^{-\frac{y^2}{2}}$
for every
![]() $y\in\mathbf{R}$
. Let R be the Markov kernel associated with independent and identically distributed (i.i.d.) sampling from the
$y\in\mathbf{R}$
. Let R be the Markov kernel associated with independent and identically distributed (i.i.d.) sampling from the
![]() $\mathrm{normal}(0,1)$
distribution, i.e.
$\mathrm{normal}(0,1)$
distribution, i.e.
![]() $R(x,\mathrm{d}y)=\frac{1}{\sqrt{2\pi}}\mathrm{e}^{-\frac{y^2}{2}}\mathrm{d}y=h(y)\mathrm{d}y$
for every
$R(x,\mathrm{d}y)=\frac{1}{\sqrt{2\pi}}\mathrm{e}^{-\frac{y^2}{2}}\mathrm{d}y=h(y)\mathrm{d}y$
for every
![]() $x\in\mathbf{R}$
.
$x\in\mathbf{R}$
.
Let
![]() $\Pi$
denote the Markov kernel associated with i.i.d. sampling from
$\Pi$
denote the Markov kernel associated with i.i.d. sampling from
![]() $\pi$
(i.e.
$\pi$
(i.e.
![]() $\Pi(x,\mathrm{d}y)=\pi(\mathrm{d}y)=\mathrm{e}^{-y}\mathrm{d}y=f(y)\mathrm{d}y$
for every
$\Pi(x,\mathrm{d}y)=\pi(\mathrm{d}y)=\mathrm{e}^{-y}\mathrm{d}y=f(y)\mathrm{d}y$
for every
![]() $x\in\mathbf{X}$
), and let Q be the Markov kernel associated with the MH algorithm with proposal R (see Example 6.1 or [Reference Roberts and Rosenthal22] for more details). (As R is simply i.i.d. sampling from a distribution, Q is also an independence sampler.) Explicitly, we have
$x\in\mathbf{X}$
), and let Q be the Markov kernel associated with the MH algorithm with proposal R (see Example 6.1 or [Reference Roberts and Rosenthal22] for more details). (As R is simply i.i.d. sampling from a distribution, Q is also an independence sampler.) Explicitly, we have
where
 \begin{align*}\alpha(x,y)=\begin{cases} \min\left\{1,\dfrac{f(y)h(x)}{f(x)h(y)}\right\}&\text{ if } f(x)h(y)\neq0,\\[10pt] 1&\text{ if } f(x)h(y)=0, \end{cases}\end{align*}
\begin{align*}\alpha(x,y)=\begin{cases} \min\left\{1,\dfrac{f(y)h(x)}{f(x)h(y)}\right\}&\text{ if } f(x)h(y)\neq0,\\[10pt] 1&\text{ if } f(x)h(y)=0, \end{cases}\end{align*}
and
![]() $\delta_x(\mathrm{d}y)$
is the point mass at
$\delta_x(\mathrm{d}y)$
is the point mass at
![]() $x\in\mathbf{R}$
for every
$x\in\mathbf{R}$
for every
![]() $x,y\in\mathbf{R}$
.
$x,y\in\mathbf{R}$
.
Trying to distinguish which algorithm, if either, of
![]() $\Pi$
and Q efficiency-dominates the other would be very difficult given only the definition of asymptotic variance. However, with Theorem 6.1 (from [Reference Peskun21] for finite state spaces and from [Reference Tierney27] for general state spaces), we shall see that it is enough to show that for
$\Pi$
and Q efficiency-dominates the other would be very difficult given only the definition of asymptotic variance. However, with Theorem 6.1 (from [Reference Peskun21] for finite state spaces and from [Reference Tierney27] for general state spaces), we shall see that it is enough to show that for
![]() $\pi$
-almost every
$\pi$
-almost every
![]() $x\in\mathbf{R}$
and measurable set
$x\in\mathbf{R}$
and measurable set
![]() $A\subseteq\mathbf{R}$
,
$A\subseteq\mathbf{R}$
,
![]() $\Pi(x,A\setminus\{x\}) \geq Q(x,A\setminus\{x\})$
, i.e. that
$\Pi(x,A\setminus\{x\}) \geq Q(x,A\setminus\{x\})$
, i.e. that
![]() $\Pi$
Peskun-dominates Q (see the end of Section 1), in order to prove that
$\Pi$
Peskun-dominates Q (see the end of Section 1), in order to prove that
![]() $\Pi$
efficiency-dominates Q. With this in mind, we simply calculate
$\Pi$
efficiency-dominates Q. With this in mind, we simply calculate
 \begin{align*} Q(x,A\setminus\{x\})\;&=\;\int_A\alpha(x,y)h(y)\mathrm{d}y\;=\;\int_{A\cap[0,\infty)}\alpha(x,y)h(y)\mathrm{d}y\\ \;&\leq\;\int_{A\cap[0,\infty)}h(y)\mathrm{d}y\;\leq\;\int_{A\cap[0,\infty)}f(y)\mathrm{d}y\;=\;\int_Af(y)\mathrm{d}y\\ \;&=\;\Pi(x,A)\;=\;\Pi(x,A\setminus\{x\}), \end{align*}
\begin{align*} Q(x,A\setminus\{x\})\;&=\;\int_A\alpha(x,y)h(y)\mathrm{d}y\;=\;\int_{A\cap[0,\infty)}\alpha(x,y)h(y)\mathrm{d}y\\ \;&\leq\;\int_{A\cap[0,\infty)}h(y)\mathrm{d}y\;\leq\;\int_{A\cap[0,\infty)}f(y)\mathrm{d}y\;=\;\int_Af(y)\mathrm{d}y\\ \;&=\;\Pi(x,A)\;=\;\Pi(x,A\setminus\{x\}), \end{align*}
as
![]() $f(y)=0$
for every
$f(y)=0$
for every
![]() $y<0$
and
$y<0$
and
![]() $h(y)\leq f(y)$
for every
$h(y)\leq f(y)$
for every
![]() $y\geq0$
, thus proving
$y\geq0$
, thus proving
![]() $\Pi$
efficiency-dominates Q by Theorem 6.1.
$\Pi$
efficiency-dominates Q by Theorem 6.1.
Although these examples are simple, they demonstrate how the theory that follows allows a much easier analysis and comparison of many algorithms, which would otherwise be impossible.
1.2. Outline of this paper
In Section 3, we provide a full proof of the formula for the asymptotic variance of
![]() $\varphi$
-irreducible reversible Markov kernels established by Kipnis and Varadhan [Reference Kipnis and Varadhan15],
$\varphi$
-irreducible reversible Markov kernels established by Kipnis and Varadhan [Reference Kipnis and Varadhan15],
by generalizing the proof of the finite-dimensional case provided by Neal and Rosenthal [Reference Neal and Rosenthal20]. We also provide a full proof of a useful and more common characterization of the asymptotic variance for aperiodic Markov kernels, relating the asymptotic variance to sums of autocovariances.
In Section 4, we use the above formula as well as some functional analysis from Section 7 to show that efficiency dominance is equivalent to a much simpler condition for reversible kernels; given Markov kernels P and Q, for every
![]() $f\in L^2_0(\pi)$
,
$f\in L^2_0(\pi)$
,
![]() $\langle f,\mathcal{P} f\rangle\leq\langle f,\mathcal{Q} f\rangle$
(Theorem 4.1). This result was first established by Mira and Geyer [Reference Mira and Geyer18] using very technical results, particularly in the ‘if’ direction of the proof. Specifically, in the ‘if’ direction they use results about monotone operator functions from Bendat and Sherman [Reference Bendat and Sherman4] (results that are generalizations of Löwner’s well-known results for monotone matrix functions [Reference Löwner16]). Neal and Rosenthal [Reference Neal and Rosenthal20] avoid these technical results in place for basic linear algebra for the case of Markov chains on finite state spaces. We generalize the approach of Neal and Rosenthal [Reference Neal and Rosenthal20] in the ‘if’ direction of the proof to general state space Markov chains. In the ‘only if’ direction however, there are difficulties with this approach that are unique to the general state space case (see the remark after Lemma 4.1). Therefore, we follow the original approach of Mira and Geyer [Reference Mira and Geyer18] for the ‘only if’ direction of the proof, which stays clear of the technical results of Bendat and Sherman [Reference Bendat and Sherman4]. Additionally, previous studies, such as [Reference Mira and Geyer18], either explicitly or implicitly require the state space to be countably generated, so that the corresponding space
$\langle f,\mathcal{P} f\rangle\leq\langle f,\mathcal{Q} f\rangle$
(Theorem 4.1). This result was first established by Mira and Geyer [Reference Mira and Geyer18] using very technical results, particularly in the ‘if’ direction of the proof. Specifically, in the ‘if’ direction they use results about monotone operator functions from Bendat and Sherman [Reference Bendat and Sherman4] (results that are generalizations of Löwner’s well-known results for monotone matrix functions [Reference Löwner16]). Neal and Rosenthal [Reference Neal and Rosenthal20] avoid these technical results in place for basic linear algebra for the case of Markov chains on finite state spaces. We generalize the approach of Neal and Rosenthal [Reference Neal and Rosenthal20] in the ‘if’ direction of the proof to general state space Markov chains. In the ‘only if’ direction however, there are difficulties with this approach that are unique to the general state space case (see the remark after Lemma 4.1). Therefore, we follow the original approach of Mira and Geyer [Reference Mira and Geyer18] for the ‘only if’ direction of the proof, which stays clear of the technical results of Bendat and Sherman [Reference Bendat and Sherman4]. Additionally, previous studies, such as [Reference Mira and Geyer18], either explicitly or implicitly require the state space to be countably generated, so that the corresponding space
![]() $L^2(\pi)$
is separable. Our proof does not require this assumption, and as such our proof generalizes the result to potentially non-countably generated state spaces. The functional analysis used in the proof of Theorem 4.1 is derived from the basics in Section 7.
$L^2(\pi)$
is separable. Our proof does not require this assumption, and as such our proof generalizes the result to potentially non-countably generated state spaces. The functional analysis used in the proof of Theorem 4.1 is derived from the basics in Section 7.
In Example 4.1, we analyse data augmentation (DA) algorithms and their sandwich variants (with operators denoted as
![]() $\mathcal{P}_{\mathrm{DA}}$
and
$\mathcal{P}_{\mathrm{DA}}$
and
![]() $\mathcal{P}_{\mathrm{S}}$
, respectively) to show that under mild conditions the sandwich variants efficiency-dominate the original DA algorithm. We follow the approach of Khare and Hobert [Reference Khare and Hobert14] to show that for every
$\mathcal{P}_{\mathrm{S}}$
, respectively) to show that under mild conditions the sandwich variants efficiency-dominate the original DA algorithm. We follow the approach of Khare and Hobert [Reference Khare and Hobert14] to show that for every
![]() $f\in L^2_0(f_X)$
,
$f\in L^2_0(f_X)$
,
![]() $\langle f,\mathcal{P}_{\mathrm{S}}f\rangle\leq\langle f,\mathcal{P}_{\mathrm{DA}}f\rangle$
. We subsequently apply Theorem 4.1 to show that the sandwich variants are always more efficient.
$\langle f,\mathcal{P}_{\mathrm{S}}f\rangle\leq\langle f,\mathcal{P}_{\mathrm{DA}}f\rangle$
. We subsequently apply Theorem 4.1 to show that the sandwich variants are always more efficient.
We use Theorem 4.1 again to give a useful one-way implication. We show that when the supremum of the spectrum of a Markov operator
![]() $\mathcal{P}$
is at least as small as the infimum of the spectrum of a second Markov operator
$\mathcal{P}$
is at least as small as the infimum of the spectrum of a second Markov operator
![]() $\mathcal{Q}$
, it follows that P efficiency-dominates Q (Proposition 4.1). In Example 4.2, we introduce common algorithms studied by Rudolf and Ullrich [Reference Rudolf and Ullrich25], whereby they prove that each algorithm has a non-negative spectrum. We use this and the previous result to show that each of these algorithms efficiency-dominates i.i.d. sampling. We use Proposition 4.1 again to show that antithetic Markov kernels are more efficient than i.i.d. sampling (Proposition 4.2), generalizing the result in [Reference Neal and Rosenthal20] in the finite state space case to the general state space case. We then give a simple toy example in Example 4.3 to give an explicit example of the theory developed so far, and to show that even in simple cases we can find value in being more efficient by using an MCMC algorithm rather than i.i.d. sampling. We further show that efficiency dominance is a partial ordering (Theorem 4.3), as shown in [Reference Mira and Geyer18].
$\mathcal{Q}$
, it follows that P efficiency-dominates Q (Proposition 4.1). In Example 4.2, we introduce common algorithms studied by Rudolf and Ullrich [Reference Rudolf and Ullrich25], whereby they prove that each algorithm has a non-negative spectrum. We use this and the previous result to show that each of these algorithms efficiency-dominates i.i.d. sampling. We use Proposition 4.1 again to show that antithetic Markov kernels are more efficient than i.i.d. sampling (Proposition 4.2), generalizing the result in [Reference Neal and Rosenthal20] in the finite state space case to the general state space case. We then give a simple toy example in Example 4.3 to give an explicit example of the theory developed so far, and to show that even in simple cases we can find value in being more efficient by using an MCMC algorithm rather than i.i.d. sampling. We further show that efficiency dominance is a partial ordering (Theorem 4.3), as shown in [Reference Mira and Geyer18].
In Section 5, we generalize the results on the efficiency dominance of combined chains in [Reference Neal and Rosenthal20] from finite state spaces to general state spaces. Given reversible Markov kernels
![]() $P_1,\ldots,P_l$
and
$P_1,\ldots,P_l$
and
![]() $Q_1,\ldots,Q_l$
, we show that if
$Q_1,\ldots,Q_l$
, we show that if
![]() $P_k$
efficiency dominates
$P_k$
efficiency dominates
![]() $Q_k$
for every k, and
$Q_k$
for every k, and
![]() $\{\alpha_1,\ldots,\alpha_l\}$
is a set of mixing probabilities, then
$\{\alpha_1,\ldots,\alpha_l\}$
is a set of mixing probabilities, then
![]() $P=\sum\alpha_kP_k$
efficiency-dominates
$P=\sum\alpha_kP_k$
efficiency-dominates
![]() $Q=\sum\alpha_kQ_k$
(Theorem 5.1). This can be used to show that a random-scan Gibbs sampler with more efficient component kernels will always be more efficient (Example 5.1). We also show that for two combined kernels differing in one component, one efficiency dominates the other if and only if its unique component kernel efficiency-dominates the other’s (Corollary 5.1). The results in Section 5 are new in the general state space case.
$Q=\sum\alpha_kQ_k$
(Theorem 5.1). This can be used to show that a random-scan Gibbs sampler with more efficient component kernels will always be more efficient (Example 5.1). We also show that for two combined kernels differing in one component, one efficiency dominates the other if and only if its unique component kernel efficiency-dominates the other’s (Corollary 5.1). The results in Section 5 are new in the general state space case.
In Section 6, we consider Peskun dominance, or dominance off the diagonal; see [Reference Peskun21, Reference Tierney27]. We say that a Markov kernel P Peskun-dominates another kernel Q if for
![]() $\pi$
-a.e.
$\pi$
-a.e.
![]() $x\in\mathbf{X}$
, for every measurable set A,
$x\in\mathbf{X}$
, for every measurable set A,
![]() $P(x,A\setminus\{x\})\geq Q(x,A\setminus\{x\})$
. We then prove Peskun dominance is a sufficient condition for efficiency dominance, first established for finite state spaces by Peskun [Reference Peskun21] and then generalized to general state spaces by Tierney [Reference Tierney27]. We start by showing that if P Peskun-dominates Q, then
$P(x,A\setminus\{x\})\geq Q(x,A\setminus\{x\})$
. We then prove Peskun dominance is a sufficient condition for efficiency dominance, first established for finite state spaces by Peskun [Reference Peskun21] and then generalized to general state spaces by Tierney [Reference Tierney27]. We start by showing that if P Peskun-dominates Q, then
![]() $\mathcal{Q}-\mathcal{P}$
is a positive operator (Lemma 6.1), just as in [Reference Tierney27]. With this established, a simple application of Theorem 4.2 completes the proof that Peskun dominance implies efficiency dominance (Theorem 6.1). We apply this theorem in Example 6.1, just as in [Reference Tierney27], to show that an MH algorithm run using a weighted sum of proposal kernels efficiency-dominates the weighted sum of MH algorithms with such proposal kernels. We then use the explicit toy example established in Section 4, Example 4.3, to show that the inverse implication of Theorem 6.1 does not hold, i.e. that efficiency dominance does not imply Peskun dominance.
$\mathcal{Q}-\mathcal{P}$
is a positive operator (Lemma 6.1), just as in [Reference Tierney27]. With this established, a simple application of Theorem 4.2 completes the proof that Peskun dominance implies efficiency dominance (Theorem 6.1). We apply this theorem in Example 6.1, just as in [Reference Tierney27], to show that an MH algorithm run using a weighted sum of proposal kernels efficiency-dominates the weighted sum of MH algorithms with such proposal kernels. We then use the explicit toy example established in Section 4, Example 4.3, to show that the inverse implication of Theorem 6.1 does not hold, i.e. that efficiency dominance does not imply Peskun dominance.
2. Background
We are given the probability space
![]() $(\mathbf{X},\mathcal{F},\pi)$
, where we assume the state space
$(\mathbf{X},\mathcal{F},\pi)$
, where we assume the state space
![]() $\mathbf{X}$
is non-empty.
$\mathbf{X}$
is non-empty.
2.1. Markov chain background
A Markov kernel on
![]() $(\mathbf{X},\mathcal{F})$
is a function
$(\mathbf{X},\mathcal{F})$
is a function
![]() $P\,:\,\mathbf{X}\times\mathcal{F}\to[0,1]$
such that
$P\,:\,\mathbf{X}\times\mathcal{F}\to[0,1]$
such that
![]() $P(x,\cdot)$
is a probability measure for every
$P(x,\cdot)$
is a probability measure for every
![]() $x\in\mathbf{X}$
, and
$x\in\mathbf{X}$
, and
![]() $P(\cdot,A)$
is a measurable function for every
$P(\cdot,A)$
is a measurable function for every
![]() $A\in\mathcal{F}$
. A time-homogeneous Markov chain
$A\in\mathcal{F}$
. A time-homogeneous Markov chain
![]() $\{X_n\}_{n\in\mathbf{N}}$
on
$\{X_n\}_{n\in\mathbf{N}}$
on
![]() $(\mathbf{X},\mathcal{F})$
has P as a Markov kernel if for every
$(\mathbf{X},\mathcal{F})$
has P as a Markov kernel if for every
![]() $n\in\mathbf{N}$
,
$n\in\mathbf{N}$
,
![]() $\left.\mathbf{P}\left(X_{n+1}\in A\right|X_n=x\right)=P(x,A)$
for every
$\left.\mathbf{P}\left(X_{n+1}\in A\right|X_n=x\right)=P(x,A)$
for every
![]() $x\in\mathbf{X}$
and
$x\in\mathbf{X}$
and
![]() $A\in\mathcal{F}$
, i.e. the Markov kernel P describes the transition probabilities of the Markov chain
$A\in\mathcal{F}$
, i.e. the Markov kernel P describes the transition probabilities of the Markov chain
![]() $\{X_n\}_{n\in\mathbf{N}}$
. The Markov kernel P is stationary with respect to
$\{X_n\}_{n\in\mathbf{N}}$
. The Markov kernel P is stationary with respect to
![]() $\pi$
if
$\pi$
if
![]() $\int_{\mathbf{X}}P(x,A)\pi(\mathrm{d}x)=\pi(A)$
for every
$\int_{\mathbf{X}}P(x,A)\pi(\mathrm{d}x)=\pi(A)$
for every
![]() $A\in\mathcal{F}$
. Intuitively, this means that once the chain
$A\in\mathcal{F}$
. Intuitively, this means that once the chain
![]() $\{X_n\}$
has reached the distribution
$\{X_n\}$
has reached the distribution
![]() $\pi$
,
$\pi$
,
![]() $X_n\sim \pi$
, then it stays at that distribution
$X_n\sim \pi$
, then it stays at that distribution
![]() $\pi$
forever,
$\pi$
forever,
![]() $X_{n+k}\sim\pi$
for every
$X_{n+k}\sim\pi$
for every
![]() $k\in\mathbf{N}$
. Thus, if the chain
$k\in\mathbf{N}$
. Thus, if the chain
![]() $\{X_n\}$
is started in stationarity, i.e.
$\{X_n\}$
is started in stationarity, i.e.
![]() $X_0\sim\pi$
, then it stays in stationarity,
$X_0\sim\pi$
, then it stays in stationarity,
![]() $X_n\sim\pi$
for every
$X_n\sim\pi$
for every
![]() $n\in\mathbf{N}$
.
$n\in\mathbf{N}$
.
The Markov kernel P is reversible with respect to
![]() $\pi$
if
$\pi$
if
![]() $P(x,\mathrm{d}y)\pi(\mathrm{d}x)=P(y,\mathrm{d}x)\pi(\mathrm{d}y)$
, i.e. the probability of starting at x distributed by
$P(x,\mathrm{d}y)\pi(\mathrm{d}x)=P(y,\mathrm{d}x)\pi(\mathrm{d}y)$
, i.e. the probability of starting at x distributed by
![]() $\pi$
and then jumping to y is the same as the probability of starting at y distributed by
$\pi$
and then jumping to y is the same as the probability of starting at y distributed by
![]() $\pi$
and then jumping to x. A Markov kernel P is
$\pi$
and then jumping to x. A Markov kernel P is
![]() $\varphi$
-irreducible if there exists a non-zero
$\varphi$
-irreducible if there exists a non-zero
![]() $\sigma$
-finite measure
$\sigma$
-finite measure
![]() $\varphi$
on
$\varphi$
on
![]() $(\mathbf{X},\mathcal{F})$
such that for every
$(\mathbf{X},\mathcal{F})$
such that for every
![]() $A\in\mathcal{F}$
with
$A\in\mathcal{F}$
with
![]() $\varphi(A)>0$
, for every
$\varphi(A)>0$
, for every
![]() $x\in\mathbf{X}$
there exists
$x\in\mathbf{X}$
there exists
![]() $n\in\mathbf{N}$
such that
$n\in\mathbf{N}$
such that
![]() $P^n(x,A)>0$
. Intuitively, the Markov chain has positive probability of eventually reaching every set of positive
$P^n(x,A)>0$
. Intuitively, the Markov chain has positive probability of eventually reaching every set of positive
![]() $\varphi$
measure.
$\varphi$
measure.
The space
![]() $L^2(\pi)$
is defined rigorously as the set of equivalence classes of
$L^2(\pi)$
is defined rigorously as the set of equivalence classes of
![]() $\pi$
-square-integrable real-valued functions, with two functions f and g being equivalent if
$\pi$
-square-integrable real-valued functions, with two functions f and g being equivalent if
![]() $f=g$
$f=g$
![]() $\pi$
-a.e., i.e.
$\pi$
-a.e., i.e.
![]() $f=g$
with probability 1. Less rigorously,
$f=g$
with probability 1. Less rigorously,
![]() $L^2(\pi)$
is simply the set of
$L^2(\pi)$
is simply the set of
![]() $\pi$
-square-integrable real-valued functions. When this set is endowed with the inner product
$\pi$
-square-integrable real-valued functions. When this set is endowed with the inner product
![]() $\langle\cdot,\cdot\rangle\,:\,L^2(\pi)\times L^2(\pi)\to\mathbf{R}$
such that
$\langle\cdot,\cdot\rangle\,:\,L^2(\pi)\times L^2(\pi)\to\mathbf{R}$
such that
![]() $(f,g)\mapsto\langle f,g\rangle\,:\!=\,\int_{\mathbf{X}}f(x)g(x)\pi(\mathrm{d}x)$
, this space becomes a real Hilbert space (a vector space that is complete with respect to the norm generated by the inner product,
$(f,g)\mapsto\langle f,g\rangle\,:\!=\,\int_{\mathbf{X}}f(x)g(x)\pi(\mathrm{d}x)$
, this space becomes a real Hilbert space (a vector space that is complete with respect to the norm generated by the inner product,
![]() $\left\lVert\cdot\right\rVert\,:\!=\,\sqrt{\langle\cdot,\cdot\rangle}$
). (When we are also dealing with complex functionals, we define the inner product instead to be
$\left\lVert\cdot\right\rVert\,:\!=\,\sqrt{\langle\cdot,\cdot\rangle}$
). (When we are also dealing with complex functionals, we define the inner product instead to be
![]() $f\times g\mapsto\langle f,g\rangle\,:\!=\,\int_{\mathbf{X}}f(x)\overline{g(x)}\pi(\mathrm{d}x)$
, where
$f\times g\mapsto\langle f,g\rangle\,:\!=\,\int_{\mathbf{X}}f(x)\overline{g(x)}\pi(\mathrm{d}x)$
, where
![]() $\overline{\alpha}$
is the complex conjugate of
$\overline{\alpha}$
is the complex conjugate of
![]() $\alpha\in\mathbf{C}$
, and
$\alpha\in\mathbf{C}$
, and
![]() $L^2(\pi)$
becomes a complex Hilbert space. As we are dealing only with real-valued functions, we do not need this distinction.)
$L^2(\pi)$
becomes a complex Hilbert space. As we are dealing only with real-valued functions, we do not need this distinction.)
Recall from Section 1 that for a function
![]() $f\in L^2(\pi)$
, its asymptotic variance with respect to the Markov kernel P, denoted v( f, P), is defined as
$f\in L^2(\pi)$
, its asymptotic variance with respect to the Markov kernel P, denoted v( f, P), is defined as
![]() $v(\,f,P)\::=\:\lim_{N\to\infty}\left[N\mathbf{Var}\left(\frac{1}{N}\sum_{k=1}^Nf(X_k)\right)\right]\:=\:\lim_{N\to\infty}\left[\frac{1}{N}\mathbf{Var}\left(\sum_{k=1}^Nf(X_k)\right)\right]$
, where
$v(\,f,P)\::=\:\lim_{N\to\infty}\left[N\mathbf{Var}\left(\frac{1}{N}\sum_{k=1}^Nf(X_k)\right)\right]\:=\:\lim_{N\to\infty}\left[\frac{1}{N}\mathbf{Var}\left(\sum_{k=1}^Nf(X_k)\right)\right]$
, where
![]() $\{X_k\}_{k\in\mathbf{N}}$
is a Markov chain with Markov kernel P started in stationarity. As is clear from our definition, the asymptotic variance is a measure of the variance of an MCMC estimate of the mean of f in the limit using the Markov chain
$\{X_k\}_{k\in\mathbf{N}}$
is a Markov chain with Markov kernel P started in stationarity. As is clear from our definition, the asymptotic variance is a measure of the variance of an MCMC estimate of the mean of f in the limit using the Markov chain
![]() $\{X_k\}$
with kernel P. Also from Section 1, recall that given two Markov kernels P and Q, both with stationary measure
$\{X_k\}$
with kernel P. Also from Section 1, recall that given two Markov kernels P and Q, both with stationary measure
![]() $\pi$
, P efficiency-dominates Q if
$\pi$
, P efficiency-dominates Q if
![]() $v(\,f,P)\:\leq\:v(\,f,Q)$
for every
$v(\,f,P)\:\leq\:v(\,f,Q)$
for every
![]() $f\in L^2(\pi)$
. Thus, if P efficiency-dominates Q, we should expect to have better estimates with use of a Markov chain with kernel P rather than a Markov chain with kernel Q. As such, when deciding on a Markov kernel to use for MCMC estimation, if P efficiency-dominates Q, we would rather use P (of course, this is if all other aspects of the kernels, such as convergence to
$f\in L^2(\pi)$
. Thus, if P efficiency-dominates Q, we should expect to have better estimates with use of a Markov chain with kernel P rather than a Markov chain with kernel Q. As such, when deciding on a Markov kernel to use for MCMC estimation, if P efficiency-dominates Q, we would rather use P (of course, this is if all other aspects of the kernels, such as convergence to
![]() $\pi$
, are similar).
$\pi$
, are similar).
For every Markov kernel P, we can define a linear operator
![]() $\mathcal{P}$
on the space of
$\mathcal{P}$
on the space of
![]() $\mathcal{F}$
measurable functions by
$\mathcal{F}$
measurable functions by
For every Markov kernel, we denote the associated linear operator defined above by its letter in a calligraphic font. If P is stationary with respect to
![]() $\pi$
, the image of
$\pi$
, the image of
![]() $\mathcal{P}$
restricted to
$\mathcal{P}$
restricted to
![]() $L^2(\pi)$
is contained in
$L^2(\pi)$
is contained in
![]() $L^2(\pi)$
, as for every
$L^2(\pi)$
, as for every
![]() $f\in L^2(\pi)$
, by Jensen’s inequality
$f\in L^2(\pi)$
, by Jensen’s inequality
and therefore
![]() $\left\lVert\mathcal{P} f\right\rVert\leq\left\lVert f\right\rVert$
for every
$\left\lVert\mathcal{P} f\right\rVert\leq\left\lVert f\right\rVert$
for every
![]() $f\in L^2(\pi)$
, so
$f\in L^2(\pi)$
, so
![]() $\mathcal{P}$
is a contraction ((1) is true for every
$\mathcal{P}$
is a contraction ((1) is true for every
![]() $1\leq r\leq\infty$
, not just
$1\leq r\leq\infty$
, not just
![]() $r=2$
; see [Reference Baxter and Rosenthal3]). In this paper, we will deal only with functions in
$r=2$
; see [Reference Baxter and Rosenthal3]). In this paper, we will deal only with functions in
![]() $L^2(\pi)$
, and thus view
$L^2(\pi)$
, and thus view
![]() $\mathcal{P}$
as a map from
$\mathcal{P}$
as a map from
![]() $L^2(\pi)\to L^2(\pi)$
, or a subset thereof.
$L^2(\pi)\to L^2(\pi)$
, or a subset thereof.
Notice that the constant function,
![]() $\unicode{x1D7D9}\,:\,\mathbf{X}\to\mathbf{R}$
such that
$\unicode{x1D7D9}\,:\,\mathbf{X}\to\mathbf{R}$
such that
![]() $\unicode{x1D7D9}(x)=1$
for every
$\unicode{x1D7D9}(x)=1$
for every
![]() $x\in\mathbf{X}$
, exists in
$x\in\mathbf{X}$
, exists in
![]() $L^2(\pi)$
(as
$L^2(\pi)$
(as
![]() $\pi$
is a probability measure), and furthermore, as
$\pi$
is a probability measure), and furthermore, as
![]() $P(x,\cdot)$
is a probability measure for every
$P(x,\cdot)$
is a probability measure for every
![]() $x\in\mathbf{X}$
,
$x\in\mathbf{X}$
,
![]() $\mathcal{P}\unicode{x1D7D9}=\unicode{x1D7D9}$
. Thus,
$\mathcal{P}\unicode{x1D7D9}=\unicode{x1D7D9}$
. Thus,
![]() $\unicode{x1D7D9}$
is an eigenfunction of
$\unicode{x1D7D9}$
is an eigenfunction of
![]() $\mathcal{P}$
with eigenvalue 1. We define the space
$\mathcal{P}$
with eigenvalue 1. We define the space
![]() $L^2_0(\pi)$
to be the subspace of
$L^2_0(\pi)$
to be the subspace of
![]() $L^2(\pi)$
perpendicular to
$L^2(\pi)$
perpendicular to
![]() $\unicode{x1D7D9}$
, or the subspace of
$\unicode{x1D7D9}$
, or the subspace of
![]() $L^2(\pi)$
functions with zero mean, i.e.
$L^2(\pi)$
functions with zero mean, i.e.
![]() $L^2_0(\pi):=\{f\in L^2(\pi)|f\perp\unicode{x1D7D9}\}=\{f\in L^2(\pi)|\langle f,\unicode{x1D7D9}\rangle=0\}=\{f\in L^2(\pi)|\mathbf{E}_{\pi}(f)=0\}$
. Notice that if
$L^2_0(\pi):=\{f\in L^2(\pi)|f\perp\unicode{x1D7D9}\}=\{f\in L^2(\pi)|\langle f,\unicode{x1D7D9}\rangle=0\}=\{f\in L^2(\pi)|\mathbf{E}_{\pi}(f)=0\}$
. Notice that if
![]() $\mathcal{P}$
is restricted to
$\mathcal{P}$
is restricted to
![]() $L^2_0(\pi)$
and P is stationary with respect to
$L^2_0(\pi)$
and P is stationary with respect to
![]() $\pi$
, then its range is contained in
$\pi$
, then its range is contained in
![]() $L^2_0(\pi)$
, as for every
$L^2_0(\pi)$
, as for every
![]() $f\in L^2_0(\pi)$
,
$f\in L^2_0(\pi)$
,
![]() $\langle\mathcal{P} f,\unicode{x1D7D9}\rangle= {\int_{x\in\mathbf{X}}\int_{y\in\mathbf{X}}f(y)P(x,\mathrm{d}y)\pi(\mathrm{d}x)=}\int_{\mathbf{X}}f(y)\pi(\mathrm{d}y)=\langle f,\unicode{x1D7D9}\rangle=0$
.
$\langle\mathcal{P} f,\unicode{x1D7D9}\rangle= {\int_{x\in\mathbf{X}}\int_{y\in\mathbf{X}}f(y)P(x,\mathrm{d}y)\pi(\mathrm{d}x)=}\int_{\mathbf{X}}f(y)\pi(\mathrm{d}y)=\langle f,\unicode{x1D7D9}\rangle=0$
.
When we are considering efficiency dominance, it is enough to look at the smaller subspace
![]() $L^2_0(\pi)$
. If P and Q are Markov kernels with stationary measure
$L^2_0(\pi)$
. If P and Q are Markov kernels with stationary measure
![]() $\pi$
, P efficiency-dominates Q if and only if P efficiency-dominates Q on the smaller subspace
$\pi$
, P efficiency-dominates Q if and only if P efficiency-dominates Q on the smaller subspace
![]() $L^2_0(\pi)$
. The forward implication is trivial as
$L^2_0(\pi)$
. The forward implication is trivial as
![]() $L^2_0(\pi)\subseteq L^2(\pi)$
, and for the converse, notice that for every
$L^2_0(\pi)\subseteq L^2(\pi)$
, and for the converse, notice that for every
![]() $f\in L^2(\pi)$
,
$f\in L^2(\pi)$
,
![]() $v(\,f,P)=v(\,f_0,P)$
and
$v(\,f,P)=v(\,f_0,P)$
and
![]() $v(\,f,Q)=v(\,f_0,Q)$
, where
$v(\,f,Q)=v(\,f_0,Q)$
, where
![]() $f_0:=f-\mathbf{E}_{\pi}(f)\in L^2_0(\pi)$
. Thus, when talking about efficiency dominance, we lose nothing by restricting ourselves to
$f_0:=f-\mathbf{E}_{\pi}(f)\in L^2_0(\pi)$
. Thus, when talking about efficiency dominance, we lose nothing by restricting ourselves to
![]() $L^2_0(\pi)$
, and we get rid of the eigenfunction
$L^2_0(\pi)$
, and we get rid of the eigenfunction
![]() $\unicode{x1D7D9}$
. Unless stated otherwise, we will consider
$\unicode{x1D7D9}$
. Unless stated otherwise, we will consider
![]() $\mathcal{P}$
as an operator on and to
$\mathcal{P}$
as an operator on and to
![]() $L^2_0(\pi)$
.
$L^2_0(\pi)$
.
A Markov kernel P is periodic with period
![]() $d\geq2$
if there exists
$d\geq2$
if there exists
![]() $\mathcal{X}_1,\ldots,\mathcal{X}_d\in\mathcal{F}$
such that
$\mathcal{X}_1,\ldots,\mathcal{X}_d\in\mathcal{F}$
such that
![]() $\mathcal{X}_k\cap\mathcal{X}_j=\emptyset$
for every
$\mathcal{X}_k\cap\mathcal{X}_j=\emptyset$
for every
![]() $j\neq k$
, and for every
$j\neq k$
, and for every
![]() $i\in\{1,\ldots,d-1\}$
,
$i\in\{1,\ldots,d-1\}$
,
![]() $P(x,\mathcal{X}_{i+1})=1$
for every
$P(x,\mathcal{X}_{i+1})=1$
for every
![]() $x\in\mathcal{X}_i$
and
$x\in\mathcal{X}_i$
and
![]() $P(x,\mathcal{X}_1)=1$
for every
$P(x,\mathcal{X}_1)=1$
for every
![]() $x\in\mathcal{X}_d$
. Intuitively, the Markov chain jumps from
$x\in\mathcal{X}_d$
. Intuitively, the Markov chain jumps from
![]() $\mathcal{X}_i$
to
$\mathcal{X}_i$
to
![]() $\mathcal{X}_{i+1}$
, then from
$\mathcal{X}_{i+1}$
, then from
![]() $\mathcal{X}_{i+1}$
to
$\mathcal{X}_{i+1}$
to
![]() $\mathcal{X}_{i+2}$
, and so on. The sets
$\mathcal{X}_{i+2}$
, and so on. The sets
![]() $\mathcal{X}_1,\ldots,\mathcal{X}_d\in\mathcal{F}$
described above are called a periodic decomposition of P. A Markov kernel P is aperiodic if it is not periodic.
$\mathcal{X}_1,\ldots,\mathcal{X}_d\in\mathcal{F}$
described above are called a periodic decomposition of P. A Markov kernel P is aperiodic if it is not periodic.
A common definition related to the efficiency of Markov kernels and a common measure in time-series analysis is the lag-k autocovariance. For an
![]() $\mathcal{F}$
-measurable function f, the lag-k autocovariance, denoted
$\mathcal{F}$
-measurable function f, the lag-k autocovariance, denoted
![]() $\gamma_k$
, is the covariance between
$\gamma_k$
, is the covariance between
![]() $f(X_0)$
and
$f(X_0)$
and
![]() $f(X_k)$
, where
$f(X_k)$
, where
![]() $\{X_k\}_{k\in\mathbf{N}}$
is a Markov chain run from stationarity with kernel P, i.e.
$\{X_k\}_{k\in\mathbf{N}}$
is a Markov chain run from stationarity with kernel P, i.e.
![]() $\gamma_k:=\mathbf{Cov}_{\pi,P}(f(X_0),f(X_k))$
. When
$\gamma_k:=\mathbf{Cov}_{\pi,P}(f(X_0),f(X_k))$
. When
![]() $\{X_k\}$
is a Markov chain run from stationarity,
$\{X_k\}$
is a Markov chain run from stationarity,
![]() $\{f(X_k)\}$
is a stationary time series, and the definition of the lag-k autocovariance is simply the regular definition from the time-series approach. When the function f is in
$\{f(X_k)\}$
is a stationary time series, and the definition of the lag-k autocovariance is simply the regular definition from the time-series approach. When the function f is in
![]() $L^2_0(\pi)$
, notice that
$L^2_0(\pi)$
, notice that
![]() $\gamma_k=\mathbf{E}_{\pi,P}(f(X_0)f(X_k))=\langle f,\mathcal{P}^kf\rangle$
.
$\gamma_k=\mathbf{E}_{\pi,P}(f(X_0)f(X_k))=\langle f,\mathcal{P}^kf\rangle$
.
We denote the Markov kernel associated with i.i.d. sampling from
![]() $\pi$
as
$\pi$
as
![]() $\Pi$
, i.e.
$\Pi$
, i.e.
![]() $\Pi\,:\,\mathbf{X}\times\mathcal{F}\to[0,\infty)$
such that
$\Pi\,:\,\mathbf{X}\times\mathcal{F}\to[0,\infty)$
such that
![]() $\Pi(x,A)=\pi(A)$
for every
$\Pi(x,A)=\pi(A)$
for every
![]() $x\in\mathbf{X}$
and
$x\in\mathbf{X}$
and
![]() $A\in\mathcal{F}$
. Notice that for every
$A\in\mathcal{F}$
. Notice that for every
![]() $f\in L^2_0(\pi)$
,
$f\in L^2_0(\pi)$
,
![]() $\Pi f(x)=\mathbf{E}_{\pi}(f)=0$
for every
$\Pi f(x)=\mathbf{E}_{\pi}(f)=0$
for every
![]() $x\in\mathbf{X}$
. Thus,
$x\in\mathbf{X}$
. Thus,
![]() $\Pi$
restricted to
$\Pi$
restricted to
![]() $L^2_0(\pi)$
is the zero function on
$L^2_0(\pi)$
is the zero function on
![]() $L^2_0(\pi)$
.
$L^2_0(\pi)$
.
2.2. Functional analysis background
Here we present some functional analysis that will be used throughout this paper. For a proper introduction to functional analysis, see [Reference Rudin24] or [Reference Conway6].
An operator T on a Hilbert space
![]() $\mathbf{H}$
(i.e. a linear function
$\mathbf{H}$
(i.e. a linear function
![]() $T\,:\,\mathbf{H}\to\mathbf{H}$
) is called bounded if there exists
$T\,:\,\mathbf{H}\to\mathbf{H}$
) is called bounded if there exists
![]() $C>0$
such that for every
$C>0$
such that for every
![]() $f\in\mathbf{H}$
,
$f\in\mathbf{H}$
,
![]() $\left\lVert Tf\right\rVert\leq C\left\lVert f\right\rVert$
. An elementary result from functional analysis shows that the operator T is continuous if and only if T is bounded in the above sense. In finite-dimensional vector spaces, all linear operators are bounded and hence continuous. The same is not true in general. The norm of a bounded operator is defined as the smallest such constant
$\left\lVert Tf\right\rVert\leq C\left\lVert f\right\rVert$
. An elementary result from functional analysis shows that the operator T is continuous if and only if T is bounded in the above sense. In finite-dimensional vector spaces, all linear operators are bounded and hence continuous. The same is not true in general. The norm of a bounded operator is defined as the smallest such constant
![]() $C>0$
such that the above holds, i.e.
$C>0$
such that the above holds, i.e.
![]() $\left\lVert T\right\rVert\,:\!=\,\inf\{C > 0\,:\left\lVert Tf\right\rVert\leq C\left\lVert f\right\rVert \mbox{for all}\,\, f\in\mathbf{H}\}$
. A bounded operator T is called invertible if it is bijective, and the inverse of T,
$\left\lVert T\right\rVert\,:\!=\,\inf\{C > 0\,:\left\lVert Tf\right\rVert\leq C\left\lVert f\right\rVert \mbox{for all}\,\, f\in\mathbf{H}\}$
. A bounded operator T is called invertible if it is bijective, and the inverse of T,
![]() $T^{-1}$
, is bounded.
$T^{-1}$
, is bounded.
Unbounded operators on
![]() $\mathbf{H}$
are linear operators T such that there is no
$\mathbf{H}$
are linear operators T such that there is no
![]() $C>0$
such that
$C>0$
such that
![]() $\left\lVert Tf\right\rVert\leq C\left\lVert f\right\rVert$
for every
$\left\lVert Tf\right\rVert\leq C\left\lVert f\right\rVert$
for every
![]() $f\in\mathbf{H}$
. Often, unbounded operators T are defined not on the whole space
$f\in\mathbf{H}$
. Often, unbounded operators T are defined not on the whole space
![]() $\mathbf{H}$
but only on a subset of
$\mathbf{H}$
but only on a subset of
![]() $\mathbf{H}$
. An unbounded operator T is densely defined if the domain of T is dense in
$\mathbf{H}$
. An unbounded operator T is densely defined if the domain of T is dense in
![]() $\mathbf{H}$
.
$\mathbf{H}$
.
The adjoint of a bounded operator T is the unique bounded operator
![]() $T^*$
such that
$T^*$
such that
![]() $\langle Tf,g\rangle=\langle f,T^*g\rangle$
for every
$\langle Tf,g\rangle=\langle f,T^*g\rangle$
for every
![]() $f,g\in\mathbf{H}$
. Similarly, if T is a densely defined operator then the adjoint of T is the linear operator
$f,g\in\mathbf{H}$
. Similarly, if T is a densely defined operator then the adjoint of T is the linear operator
![]() $T^*$
such that
$T^*$
such that
![]() $\langle Tf,g\rangle=\langle f,T^*g\rangle$
for every
$\langle Tf,g\rangle=\langle f,T^*g\rangle$
for every
![]() $f\in\textrm{domain}(T)$
and
$f\in\textrm{domain}(T)$
and
![]() $g\in\mathbf{H}$
such that
$g\in\mathbf{H}$
such that
![]() $f\mapsto\langle Tf,g\rangle$
is a bounded linear functional on
$f\mapsto\langle Tf,g\rangle$
is a bounded linear functional on
![]() $\textrm{domain}(T)$
. Thus, we define
$\textrm{domain}(T)$
. Thus, we define
![]() $\textrm{domain}(T^*)\,:\!=\,\{g\in\mathbf{H}|f\mapsto\langle Tf,g\rangle \text{ is a boundedlinear functional on }\textrm{domain}(T)\}$
. These two definitions are equivalent when T is bounded.
$\textrm{domain}(T^*)\,:\!=\,\{g\in\mathbf{H}|f\mapsto\langle Tf,g\rangle \text{ is a boundedlinear functional on }\textrm{domain}(T)\}$
. These two definitions are equivalent when T is bounded.
A bounded operator T is called normal if T commutes with its adjoint,
![]() $TT^*=T^*T$
, and is called self-adjoint if T equals its adjoint,
$TT^*=T^*T$
, and is called self-adjoint if T equals its adjoint,
![]() $T=T^*$
. Equivalently, a bounded operator T is self-adjoint if
$T=T^*$
. Equivalently, a bounded operator T is self-adjoint if
![]() $\langle Tf,g\rangle=\langle f,Tg\rangle$
for every f and
$\langle Tf,g\rangle=\langle f,Tg\rangle$
for every f and
![]() $g\in\mathbf{H}$
. A densely defined operator T is called self-adjoint if
$g\in\mathbf{H}$
. A densely defined operator T is called self-adjoint if
![]() $T=T^*$
and
$T=T^*$
and
![]() $\textrm{domain}(T)=\textrm{domain}(T^*)$
.
$\textrm{domain}(T)=\textrm{domain}(T^*)$
.
![]() $\mathcal{P}$
restricted to
$\mathcal{P}$
restricted to
![]() $L^2(\pi)$
is self-adjoint if and only if P is reversible. As
$L^2(\pi)$
is self-adjoint if and only if P is reversible. As
![]() $L^2_0(\pi)\subseteq L^2(\pi)$
, if P is reversible with respect to
$L^2_0(\pi)\subseteq L^2(\pi)$
, if P is reversible with respect to
![]() $\pi$
then
$\pi$
then
![]() $\mathcal{P}$
restricted to
$\mathcal{P}$
restricted to
![]() $L^2_0(\pi)$
is self-adjoint as well.
$L^2_0(\pi)$
is self-adjoint as well.
The spectrum of an operator T is the subset
![]() $\sigma(T):=\{\lambda\in\mathbf{C}|T-\lambda\mathcal{I}\text{ is not invertible}\}$
of the complex plane, where
$\sigma(T):=\{\lambda\in\mathbf{C}|T-\lambda\mathcal{I}\text{ is not invertible}\}$
of the complex plane, where
![]() $\mathcal{I}$
is the identity operator. Note that in the above definition, ‘invertible’ is meant in the context of bounded linear operators, i.e. T is bijective and the inverse of T,
$\mathcal{I}$
is the identity operator. Note that in the above definition, ‘invertible’ is meant in the context of bounded linear operators, i.e. T is bijective and the inverse of T,
![]() $T^{-1}$
, is also bounded. If the operator T is self-adjoint, the spectrum of T is real, i.e.
$T^{-1}$
, is also bounded. If the operator T is self-adjoint, the spectrum of T is real, i.e.
![]() $\sigma(T)\subseteq\mathbf{R}$
(see Theorem 12.26(a) in [Reference Rudin24]). It is important to note that if the underlying Hilbert space of the operator T is finite-dimensional, as is the case for
$\sigma(T)\subseteq\mathbf{R}$
(see Theorem 12.26(a) in [Reference Rudin24]). It is important to note that if the underlying Hilbert space of the operator T is finite-dimensional, as is the case for
![]() $L^2(\pi)$
and
$L^2(\pi)$
and
![]() $L^2_0(\pi)$
when
$L^2_0(\pi)$
when
![]() $\mathbf{X}$
is finite, then the spectrum of T is exactly the set of eigenvalues of T. When the Hilbert space is not finite-dimensional, the spectrum also includes limit points and points where
$\mathbf{X}$
is finite, then the spectrum of T is exactly the set of eigenvalues of T. When the Hilbert space is not finite-dimensional, the spectrum also includes limit points and points where
![]() $T-\lambda\mathcal{I}$
is not surjective.
$T-\lambda\mathcal{I}$
is not surjective.
An operator T on a Hilbert space
![]() $\mathbf{H}$
is called positive if for every
$\mathbf{H}$
is called positive if for every
![]() $f\in\mathbf{H}$
,
$f\in\mathbf{H}$
,
![]() $\langle f,Tf\rangle\geq0$
. As we shall see in Lemma 4.4, if T is bounded and normal then T is positive if and only if the spectrum of T is positive, i.e.
$\langle f,Tf\rangle\geq0$
. As we shall see in Lemma 4.4, if T is bounded and normal then T is positive if and only if the spectrum of T is positive, i.e.
![]() $\sigma(T)\subseteq[0,\infty)$
. It is important to note that when the Hilbert space
$\sigma(T)\subseteq[0,\infty)$
. It is important to note that when the Hilbert space
![]() $\mathbf{H}$
is a real Hilbert space, it is not necessarily true that if T is positive and bounded then T is self-adjoint. This is an important distinction, as this is true when
$\mathbf{H}$
is a real Hilbert space, it is not necessarily true that if T is positive and bounded then T is self-adjoint. This is an important distinction, as this is true when
![]() $\mathbf{H}$
is a complex Hilbert space.
$\mathbf{H}$
is a complex Hilbert space.
Furthermore, as shown by the inequality (1), (which is equivalent to
![]() $\left\lVert\mathcal{P} f\right\rVert^2\leq\left\lVert f\right\rVert^2$
), when P is stationary with respect to
$\left\lVert\mathcal{P} f\right\rVert^2\leq\left\lVert f\right\rVert^2$
), when P is stationary with respect to
![]() $\pi$
, the norm of
$\pi$
, the norm of
![]() $\mathcal{P}$
on
$\mathcal{P}$
on
![]() $L^2(\pi)$
is less than or equal to 1. This also bounds the spectrum of
$L^2(\pi)$
is less than or equal to 1. This also bounds the spectrum of
![]() $\mathcal{P}$
to
$\mathcal{P}$
to
![]() $\lambda\in\mathbf{C}$
such that
$\lambda\in\mathbf{C}$
such that
![]() $|\lambda|\leq\left\lVert\mathcal{P}\right\rVert\leq1$
. If P is reversible then
$|\lambda|\leq\left\lVert\mathcal{P}\right\rVert\leq1$
. If P is reversible then
![]() $\mathcal{P}$
is self-adjoint and thus the spectrum of
$\mathcal{P}$
is self-adjoint and thus the spectrum of
![]() $\mathcal{P}$
is real,
$\mathcal{P}$
is real,
![]() $\sigma(\mathcal{P})\subseteq\mathbf{R}$
. Thus, if P is reversible with respect to
$\sigma(\mathcal{P})\subseteq\mathbf{R}$
. Thus, if P is reversible with respect to
![]() $\pi$
then
$\pi$
then
![]() $\sigma(\mathcal{P})\subseteq[\!-1,1]$
.
$\sigma(\mathcal{P})\subseteq[\!-1,1]$
.
Given a bounded self-adjoint operator T on the Hilbert space
![]() $\mathbf{H}$
, by the spectral theorem (see Theorem 12.23 in [Reference Rudin24] and Theorem 2.2 in Chapter 9 in [Reference Conway6]), we know that there exists a spectral measure
$\mathbf{H}$
, by the spectral theorem (see Theorem 12.23 in [Reference Rudin24] and Theorem 2.2 in Chapter 9 in [Reference Conway6]), we know that there exists a spectral measure
![]() $\mathcal{E}_T\,:\,\mathcal{B}(\sigma(T))\to\mathfrak{B}(\mathbf{H})$
such that
$\mathcal{E}_T\,:\,\mathcal{B}(\sigma(T))\to\mathfrak{B}(\mathbf{H})$
such that
![]() $T=\int_{\sigma(T)}\lambda\mathcal{E}_T(\mathrm{d}\lambda)$
.
$T=\int_{\sigma(T)}\lambda\mathcal{E}_T(\mathrm{d}\lambda)$
.
![]() $\mathcal{B}(\sigma(T))$
denotes the Borel
$\mathcal{B}(\sigma(T))$
denotes the Borel
![]() $\sigma$
-field of
$\sigma$
-field of
![]() $\sigma(T)\subseteq\mathbf{C}$
and
$\sigma(T)\subseteq\mathbf{C}$
and
![]() $\mathfrak{B}(\mathbf{H})$
denotes the set of bounded operators on the Hilbert space
$\mathfrak{B}(\mathbf{H})$
denotes the set of bounded operators on the Hilbert space
![]() $\mathbf{H}$
. So when P is reversible,
$\mathbf{H}$
. So when P is reversible,
![]() $\mathcal{P}$
is self-adjoint, and thus by the spectral theorem,
$\mathcal{P}$
is self-adjoint, and thus by the spectral theorem,
![]() $\mathcal{P}\;=\;\int_{\sigma(\mathcal{P})}\lambda\,\mathcal{E}_{\mathcal{P}}(\mathrm{d}\lambda)$
, where
$\mathcal{P}\;=\;\int_{\sigma(\mathcal{P})}\lambda\,\mathcal{E}_{\mathcal{P}}(\mathrm{d}\lambda)$
, where
![]() $\mathcal{E}_{\mathcal{P}}$
is the spectral measure of
$\mathcal{E}_{\mathcal{P}}$
is the spectral measure of
![]() $\mathcal{P}$
.
$\mathcal{P}$
.
The spectral measure
![]() $\mathcal{E}_T$
satisfies (i)
$\mathcal{E}_T$
satisfies (i)
![]() $\mathcal{E}_T(\emptyset)=0$
and
$\mathcal{E}_T(\emptyset)=0$
and
![]() $\mathcal{E}_T(\sigma (T))=\mathcal{I}$
, (ii) for every
$\mathcal{E}_T(\sigma (T))=\mathcal{I}$
, (ii) for every
![]() $A\in\mathcal{B}(\sigma(T))$
,
$A\in\mathcal{B}(\sigma(T))$
,
![]() $\mathcal{E}_T(A)\in\mathfrak{B}(\mathbf{H})$
is a self-adjoint projection, i.e.
$\mathcal{E}_T(A)\in\mathfrak{B}(\mathbf{H})$
is a self-adjoint projection, i.e.
![]() $\mathcal{E}_T(A)=\mathcal{E}_T(A)^2=\mathcal{E}_T(A)^*$
, (iii) for every
$\mathcal{E}_T(A)=\mathcal{E}_T(A)^2=\mathcal{E}_T(A)^*$
, (iii) for every
![]() $A_1,A_2\in\mathcal{B}(\sigma(T))$
,
$A_1,A_2\in\mathcal{B}(\sigma(T))$
,
![]() $\mathcal{E}_T(A_1\cap A_2)=\mathcal{E}_T(A_1)\mathcal{E}_T(A_2)$
, and (iv) for every sequence of disjoint subsets
$\mathcal{E}_T(A_1\cap A_2)=\mathcal{E}_T(A_1)\mathcal{E}_T(A_2)$
, and (iv) for every sequence of disjoint subsets
![]() $\{A_n\}_{n\in\mathbf{N}}\subseteq\mathcal{B}(\sigma(T))$
,
$\{A_n\}_{n\in\mathbf{N}}\subseteq\mathcal{B}(\sigma(T))$
,
![]() $\mathcal{E}_T\left(\bigcup_{n\in\mathbf{N}}A_n\right)=\sum_{n\in\mathbf{N}}\mathcal{E}_T(A_n)$
.
$\mathcal{E}_T\left(\bigcup_{n\in\mathbf{N}}A_n\right)=\sum_{n\in\mathbf{N}}\mathcal{E}_T(A_n)$
.
Although this definition and the decomposition of T above may seem complicated, recall from linear algebra that when
![]() $\mathbf{H}$
is finite-dimensional, we can decompose a self-adjoint operator T as
$\mathbf{H}$
is finite-dimensional, we can decompose a self-adjoint operator T as
![]() $T=\sum_{k=0}^{n-1}\lambda_kP_k$
, where
$T=\sum_{k=0}^{n-1}\lambda_kP_k$
, where
![]() $\{\lambda_k\}_{k=0}^{n-1}\subseteq\mathbf{C}$
are the eigenvalues of T and
$\{\lambda_k\}_{k=0}^{n-1}\subseteq\mathbf{C}$
are the eigenvalues of T and
![]() $P_k\,:\,\mathbf{H}\to\mathbf{H}$
is the projection onto the eigenspace of
$P_k\,:\,\mathbf{H}\to\mathbf{H}$
is the projection onto the eigenspace of
![]() $\lambda_k$
. This is not so different from the above, except that when
$\lambda_k$
. This is not so different from the above, except that when
![]() $\mathbf{H}$
is allowed to be infinite-dimensional, this sum of projections becomes an integral of projections.
$\mathbf{H}$
is allowed to be infinite-dimensional, this sum of projections becomes an integral of projections.
For every
![]() $f\in\mathbf{H}$
, we define the induced measure
$f\in\mathbf{H}$
, we define the induced measure
![]() $\mathcal{E}_{f,T}$
on
$\mathcal{E}_{f,T}$
on
![]() $\mathbf{C}$
as
$\mathbf{C}$
as
![]() $\mathcal{E}_{f,T}(A):=\langle f,\mathcal{E}_{T}(A)f\rangle$
for every Borel measurable set
$\mathcal{E}_{f,T}(A):=\langle f,\mathcal{E}_{T}(A)f\rangle$
for every Borel measurable set
![]() $A\subseteq\mathbf{C}$
. Note that as
$A\subseteq\mathbf{C}$
. Note that as
![]() $\mathcal{E}_T(A)$
is a self-adjoint projection for every Borel measurable set
$\mathcal{E}_T(A)$
is a self-adjoint projection for every Borel measurable set
![]() $A\subseteq\mathbf{C}$
, the measure
$A\subseteq\mathbf{C}$
, the measure
![]() $\mathcal{E}_{f,T}$
on
$\mathcal{E}_{f,T}$
on
![]() $\mathbf{C}$
is a positive measure. For every Borel measurable function
$\mathbf{C}$
is a positive measure. For every Borel measurable function
![]() $\phi\,:\,\mathbf{C}\to\mathbf{C}$
, the operator
$\phi\,:\,\mathbf{C}\to\mathbf{C}$
, the operator
![]() $\phi(T)$
on
$\phi(T)$
on
![]() $\mathbf{H}$
is defined as
$\mathbf{H}$
is defined as
![]() $\phi(T):=\int\phi(\lambda)\mathcal{E}_{T}(\mathrm{d}\lambda)$
.
$\phi(T):=\int\phi(\lambda)\mathcal{E}_{T}(\mathrm{d}\lambda)$
.
![]() $\phi(T)$
is a bounded operator whenever the function
$\phi(T)$
is a bounded operator whenever the function
![]() $\phi$
is bounded. Putting this together with our definition of
$\phi$
is bounded. Putting this together with our definition of
![]() $\mathcal{E}_{f,T}$
, for every bounded Borel measurable function
$\mathcal{E}_{f,T}$
, for every bounded Borel measurable function
![]() $\phi:\mathbf{C}\to\mathbf{C}$
and for every
$\phi:\mathbf{C}\to\mathbf{C}$
and for every
![]() $f\in\mathbf{H}$
, we have
$f\in\mathbf{H}$
, we have
We will also usually assume that the Markov kernel P is
![]() $\varphi$
-irreducible, as when P is
$\varphi$
-irreducible, as when P is
![]() $\varphi$
-irreducible, the constant function is the only eigenfunction (up to a scalar multiple) of
$\varphi$
-irreducible, the constant function is the only eigenfunction (up to a scalar multiple) of
![]() $\mathcal{P}$
with eigenvalue 1 (see Lemma 4.7.4 in [Reference Gallegos-Herrada, Ledvinka and Rosenthal10]). Thus, if P is
$\mathcal{P}$
with eigenvalue 1 (see Lemma 4.7.4 in [Reference Gallegos-Herrada, Ledvinka and Rosenthal10]). Thus, if P is
![]() $\varphi$
-irreducible, by restricting ourselves to
$\varphi$
-irreducible, by restricting ourselves to
![]() $L^2_0(\pi)$
, we get rid of the eigenvalue 1, i.e. 1 is not an eigenvalue of
$L^2_0(\pi)$
, we get rid of the eigenvalue 1, i.e. 1 is not an eigenvalue of
![]() $\mathcal{P}$
on
$\mathcal{P}$
on
![]() $L^2_0(\pi)$
. Note, however, that this does not mean that
$L^2_0(\pi)$
. Note, however, that this does not mean that
![]() $1\notin\sigma(\mathcal{P})$
when we restrict ourselves to
$1\notin\sigma(\mathcal{P})$
when we restrict ourselves to
![]() $L^2_0(\pi)$
, as
$L^2_0(\pi)$
, as
![]() $(\mathcal{P}-\mathcal{I})^{-1}$
could still be unbounded.
$(\mathcal{P}-\mathcal{I})^{-1}$
could still be unbounded.
3. Asymptotic Variance
We now provide a detailed proof of the formula for the asymptotic variance of
![]() $\varphi$
-irreducible reversible Markov kernels, originally introduced by Kipnis and Varadhan [Reference Kipnis and Varadhan15] by generalizing the proof of the finite state space case from [Reference Neal and Rosenthal20] to the general state space case. Also in this section, we prove another, more familiar and practical characterization of the asymptotic variance for
$\varphi$
-irreducible reversible Markov kernels, originally introduced by Kipnis and Varadhan [Reference Kipnis and Varadhan15] by generalizing the proof of the finite state space case from [Reference Neal and Rosenthal20] to the general state space case. Also in this section, we prove another, more familiar and practical characterization of the asymptotic variance for
![]() $\varphi$
-irreducible reversible aperiodic Markov kernels (see [Reference Geyer11–Reference Jones13]), again generalizing the proof from [Reference Neal and Rosenthal20].
$\varphi$
-irreducible reversible aperiodic Markov kernels (see [Reference Geyer11–Reference Jones13]), again generalizing the proof from [Reference Neal and Rosenthal20].
Theorem 3.1. If P is a
![]() $\varphi$
-irreducible reversible Markov kernel with stationary distribution
$\varphi$
-irreducible reversible Markov kernel with stationary distribution
![]() $\pi$
, then for every
$\pi$
, then for every
![]() $f\in L^2_0(\pi)$
,
$f\in L^2_0(\pi)$
,
where
![]() $\mathcal{E}_{f,\mathcal{P}}$
is the measure induced by the spectral measure of
$\mathcal{E}_{f,\mathcal{P}}$
is the measure induced by the spectral measure of
![]() $\mathcal{P}$
(see Section 2.2). Note, however, that this may still diverge to infinity.
$\mathcal{P}$
(see Section 2.2). Note, however, that this may still diverge to infinity.
Proof. For every
![]() $f\in L^2_0(\pi)$
, by expanding the squares of
$f\in L^2_0(\pi)$
, by expanding the squares of
![]() $\mathbf{Var}_{\pi,P}\left(\sum_{k=1}^Nf(X_k)\right)$
, as
$\mathbf{Var}_{\pi,P}\left(\sum_{k=1}^Nf(X_k)\right)$
, as
![]() $\mathbf{E}_{\pi}(f)=0$
(by the definition of
$\mathbf{E}_{\pi}(f)=0$
(by the definition of
![]() $L^2_0(\pi)$
), we have
$L^2_0(\pi)$
), we have
 \begin{align} \frac{1}{N}\mathbf{Var}_{\pi,P}\left(\sum_{k=1}^Nf(X_k)\right)\,&=\,\frac{1}{N}\sum_{k=1}^N\sum_{n=1}^N\mathbf{E}_{\pi,P}\left(f(X_k)f(X_n)\right)\nonumber\\ \,&=\,\frac{1}{N}\sum_{k=1}^N\sum_{n=1}^N\mathbf{E}_{\pi,P}\left(f(X_0)f(X_{|n-k|})\right)\nonumber\\ \,&=\,\left\lVert f\right\rVert^2+2\sum_{k=1}^N\left(\frac{N-k}{N}\right)\langle f,\mathcal{P}^kf\rangle. \end{align}
\begin{align} \frac{1}{N}\mathbf{Var}_{\pi,P}\left(\sum_{k=1}^Nf(X_k)\right)\,&=\,\frac{1}{N}\sum_{k=1}^N\sum_{n=1}^N\mathbf{E}_{\pi,P}\left(f(X_k)f(X_n)\right)\nonumber\\ \,&=\,\frac{1}{N}\sum_{k=1}^N\sum_{n=1}^N\mathbf{E}_{\pi,P}\left(f(X_0)f(X_{|n-k|})\right)\nonumber\\ \,&=\,\left\lVert f\right\rVert^2+2\sum_{k=1}^N\left(\frac{N-k}{N}\right)\langle f,\mathcal{P}^kf\rangle. \end{align}
Thus, as
![]() $\langle f,\mathcal{P}^kf\rangle\:=\:\int_{\sigma(\mathcal{P})}\lambda^k\,\mathcal{E}_{f,\mathcal{P}}(\mathrm{d}\lambda)$
for every
$\langle f,\mathcal{P}^kf\rangle\:=\:\int_{\sigma(\mathcal{P})}\lambda^k\,\mathcal{E}_{f,\mathcal{P}}(\mathrm{d}\lambda)$
for every
![]() $k\in\mathbf{N}$
,
$k\in\mathbf{N}$
,
 \begin{align} v(\,f,P) &\,=\,\lim_{N\to\infty}\left[\frac{1}{N} \mathbf{Var}\left(\sum_{n=1}^Nf(X_n)\right)\right]\nonumber\\ &\,=\,\lim_{N\to\infty}\left[\left\lVert f\right\rVert^2+2\sum_{k=1}^N \left(\frac{N-k}{N}\right)\langle f,\mathcal{P}^kf\rangle\right]\nonumber\\ &\,=\,\left\lVert f\right\rVert^2+2\lim_{N\to\infty} \left[\int_{\lambda\in\sigma(\mathcal{P})}\sum_{k=1}^{\infty} \mathbf{1}_{k\leq N}(k)\left(\frac{N-k}{N}\right) \lambda^k\mathcal{E}_{f,\mathcal{P}}(\mathrm{d}\lambda)\right]. \end{align}
\begin{align} v(\,f,P) &\,=\,\lim_{N\to\infty}\left[\frac{1}{N} \mathbf{Var}\left(\sum_{n=1}^Nf(X_n)\right)\right]\nonumber\\ &\,=\,\lim_{N\to\infty}\left[\left\lVert f\right\rVert^2+2\sum_{k=1}^N \left(\frac{N-k}{N}\right)\langle f,\mathcal{P}^kf\rangle\right]\nonumber\\ &\,=\,\left\lVert f\right\rVert^2+2\lim_{N\to\infty} \left[\int_{\lambda\in\sigma(\mathcal{P})}\sum_{k=1}^{\infty} \mathbf{1}_{k\leq N}(k)\left(\frac{N-k}{N}\right) \lambda^k\mathcal{E}_{f,\mathcal{P}}(\mathrm{d}\lambda)\right]. \end{align}
To deal with the limit in (4), we split the integral over
![]() $\sigma(\mathcal{P})$
into three subsets, (0,1),
$\sigma(\mathcal{P})$
into three subsets, (0,1),
![]() $(\!-1,0]$
, and
$(\!-1,0]$
, and
![]() $\{-1\}$
. (Recall from Section 2 that
$\{-1\}$
. (Recall from Section 2 that
![]() $\sigma(\mathcal{P})\subseteq[\!-1,1]$
, and notice that we do not need to worry about
$\sigma(\mathcal{P})\subseteq[\!-1,1]$
, and notice that we do not need to worry about
![]() $\{1\}$
, as 1 is not an eigenvalue of
$\{1\}$
, as 1 is not an eigenvalue of
![]() $\mathcal{P}$
on
$\mathcal{P}$
on
![]() $L^2_0(\pi)$
as P is
$L^2_0(\pi)$
as P is
![]() $\varphi$
-irreducible [see Section 2.1], and thus
$\varphi$
-irreducible [see Section 2.1], and thus
![]() $\mathcal{E}_{f,\mathcal{P}}(\{1\})=0$
by Lemma 3.1).
$\mathcal{E}_{f,\mathcal{P}}(\{1\})=0$
by Lemma 3.1).
For the first two subsets, for every fixed
![]() $\lambda\in(\!-1,0]\cup(0,1)=(\!-1,1)$
, notice that for every
$\lambda\in(\!-1,0]\cup(0,1)=(\!-1,1)$
, notice that for every
![]() $N\in\mathbf{N}$
,
$N\in\mathbf{N}$
,
so the sum is absolutely summable. Thus, we can pull the pointwise limit through and show that for every
![]() $\lambda\in(\!-1,1)$
, by the geometric series
$\lambda\in(\!-1,1)$
, by the geometric series
![]() $\sum_{k=1}^{\infty}r^k=\frac{r}{1-r}$
,
$\sum_{k=1}^{\infty}r^k=\frac{r}{1-r}$
,
![]() $\lim_{N\to\infty}$
$\lim_{N\to\infty}$
![]() $\left[\sum_{k=1}^{\infty}\mathbf{1}_{k\leq N}(k) \left(\frac{N-k}{N}\right)\lambda^k\right] =\frac{\lambda}{1-\lambda}$
.
$\left[\sum_{k=1}^{\infty}\mathbf{1}_{k\leq N}(k) \left(\frac{N-k}{N}\right)\lambda^k\right] =\frac{\lambda}{1-\lambda}$
.
By the monotone convergence theorem for
![]() $\lambda \in(0,1)$
and the dominated convergence theorem for
$\lambda \in(0,1)$
and the dominated convergence theorem for
![]() $\lambda\in(\!-1,0]$
,
$\lambda\in(\!-1,0]$
,
 \begin{equation} \lim_{N\to\infty}\left[\int_{\lambda\in(0,1)}\sum_{k=1}^{\infty} \mathbf{1}_{k\leq N}(k)\left(\frac{N-k}{N}\right)\lambda^k\mathcal{E}_{f,\mathcal{P}}(\mathrm{d}\lambda)\right] \,=\,\int_{\lambda\in(0,1)}\frac{\lambda}{1-\lambda}\mathcal{E}_{f,\mathcal{P}}(\mathrm{d}\lambda) \end{equation}
\begin{equation} \lim_{N\to\infty}\left[\int_{\lambda\in(0,1)}\sum_{k=1}^{\infty} \mathbf{1}_{k\leq N}(k)\left(\frac{N-k}{N}\right)\lambda^k\mathcal{E}_{f,\mathcal{P}}(\mathrm{d}\lambda)\right] \,=\,\int_{\lambda\in(0,1)}\frac{\lambda}{1-\lambda}\mathcal{E}_{f,\mathcal{P}}(\mathrm{d}\lambda) \end{equation}
and
 \begin{equation} \lim_{N\to\infty}\left[\int_{\lambda\in(\!-1,0]}\sum_{k=1}^{\infty} \mathbf{1}_{k\leq N}(k)\left(\frac{N-k}{N}\right)\lambda^k\mathcal{E}_{f,\mathcal{P}}(\mathrm{d}\lambda)\right] \,=\,\int_{\lambda\in(\!-1,0]}\frac{\lambda}{1-\lambda}\mathcal{E}_{f,\mathcal{P}}(\mathrm{d}\lambda). \end{equation}
\begin{equation} \lim_{N\to\infty}\left[\int_{\lambda\in(\!-1,0]}\sum_{k=1}^{\infty} \mathbf{1}_{k\leq N}(k)\left(\frac{N-k}{N}\right)\lambda^k\mathcal{E}_{f,\mathcal{P}}(\mathrm{d}\lambda)\right] \,=\,\int_{\lambda\in(\!-1,0]}\frac{\lambda}{1-\lambda}\mathcal{E}_{f,\mathcal{P}}(\mathrm{d}\lambda). \end{equation}
For the last case, the case of
![]() $\{-1\}$
, notice that for every
$\{-1\}$
, notice that for every
![]() $N\in\mathbf{N}$
(simplifying the equation found in [Reference Neal and Rosenthal20]), denoting the floor of
$N\in\mathbf{N}$
(simplifying the equation found in [Reference Neal and Rosenthal20]), denoting the floor of
![]() $x\in\mathbf{R}$
as
$x\in\mathbf{R}$
as
![]() $\lfloor x\rfloor$
, we have
$\lfloor x\rfloor$
, we have
 \begin{align*} \sum_{k=1}^{\infty}\mathbf{1}_{k\leq N}(k)\frac{N-k}{N}(\!-1)^k\mathcal{E}_{f,\mathcal{P}} (\{-1\}) \:&=\:\mathcal{E}_{f,\mathcal{P}}(\{-1\})N^{-1}\sum_{k=1}^{N}\left[(\!-1)^k(N-k)\right]\\[5pt] \:&=\:\mathcal{E}_{f,\mathcal{P}}(\{-1\})N^{-1}\sum_{m=1}^{\lfloor N/2\rfloor}\left[(N-2m) -(N-2m+1)\right]\\[5pt] \:&=\:\mathcal{E}_{f,\mathcal{P}}(\{-1\})N^{-1}\sum_{m=1}^{\lfloor N/2\rfloor}\left(\!-1\right)=\left(\frac{\lfloor-N/2\rfloor}{N}\right)\mathcal{E}_{f,\mathcal{P}}(\{-1\}).\nonumber \end{align*}
\begin{align*} \sum_{k=1}^{\infty}\mathbf{1}_{k\leq N}(k)\frac{N-k}{N}(\!-1)^k\mathcal{E}_{f,\mathcal{P}} (\{-1\}) \:&=\:\mathcal{E}_{f,\mathcal{P}}(\{-1\})N^{-1}\sum_{k=1}^{N}\left[(\!-1)^k(N-k)\right]\\[5pt] \:&=\:\mathcal{E}_{f,\mathcal{P}}(\{-1\})N^{-1}\sum_{m=1}^{\lfloor N/2\rfloor}\left[(N-2m) -(N-2m+1)\right]\\[5pt] \:&=\:\mathcal{E}_{f,\mathcal{P}}(\{-1\})N^{-1}\sum_{m=1}^{\lfloor N/2\rfloor}\left(\!-1\right)=\left(\frac{\lfloor-N/2\rfloor}{N}\right)\mathcal{E}_{f,\mathcal{P}}(\{-1\}).\nonumber \end{align*}
Thus, as
![]() $\lim_{N\to\infty}\frac{\lfloor-N/2\rfloor}{N}=-1/2$
, we have the pointwise limit
$\lim_{N\to\infty}\frac{\lfloor-N/2\rfloor}{N}=-1/2$
, we have the pointwise limit
 \begin{align} \lim_{N\to\infty}\sum_{k=1}^{\infty} \mathbf{1}_{k\leq N}(k)\left(\frac{N-k}{N}\right)\left(\!-1\right)^k\mathcal{E}_{f,\mathcal{P}}(\{-1\}) \;&=\;\left(\frac{-1}{2}\right)\mathcal{E}_{f,\mathcal{P}}(\{-1\})\nonumber\\[5pt]\;&=\; \left(\frac{\lambda}{1-\lambda}\right)\mathcal{E}_{f,\mathcal{P}}(\{\lambda\})|_{\lambda=-1}. \end{align}
\begin{align} \lim_{N\to\infty}\sum_{k=1}^{\infty} \mathbf{1}_{k\leq N}(k)\left(\frac{N-k}{N}\right)\left(\!-1\right)^k\mathcal{E}_{f,\mathcal{P}}(\{-1\}) \;&=\;\left(\frac{-1}{2}\right)\mathcal{E}_{f,\mathcal{P}}(\{-1\})\nonumber\\[5pt]\;&=\; \left(\frac{\lambda}{1-\lambda}\right)\mathcal{E}_{f,\mathcal{P}}(\{\lambda\})|_{\lambda=-1}. \end{align}
To split the integral in (4) into our three pieces, (0,1),
![]() $(\!-1,0]$
, and
$(\!-1,0]$
, and
![]() $\{-1\}$
, and pull the limit through, we have to verify that if we do pull the limit through, we are not performing
$\{-1\}$
, and pull the limit through, we have to verify that if we do pull the limit through, we are not performing
![]() $\infty-\infty$
. To verify this, it is enough to show that
$\infty-\infty$
. To verify this, it is enough to show that
![]() $\left|\lim_{N\to\infty}\int_{\lambda\in(\!-1,0]}\sum_{k=1}^{\infty}\mathbf{1}_{k\leq N}(k) \left(\frac{N-k}{N}\right)\lambda^k\mathcal{E}_{f,\mathcal{P}}(\mathrm{d}\lambda)\right|$
and
$\left|\lim_{N\to\infty}\int_{\lambda\in(\!-1,0]}\sum_{k=1}^{\infty}\mathbf{1}_{k\leq N}(k) \left(\frac{N-k}{N}\right)\lambda^k\mathcal{E}_{f,\mathcal{P}}(\mathrm{d}\lambda)\right|$
and
![]() $\left|\lim_{N\to\infty}\sum_{k=1}^{\infty}\mathbf{1}_{k\leq N}(k) \left(\frac{N-k}{N}\right)\mathcal{E}_{f,\mathcal{P}}(\{-1\})\right|$
are finite. So by (6) and (7), we find that
$\left|\lim_{N\to\infty}\sum_{k=1}^{\infty}\mathbf{1}_{k\leq N}(k) \left(\frac{N-k}{N}\right)\mathcal{E}_{f,\mathcal{P}}(\{-1\})\right|$
are finite. So by (6) and (7), we find that
![]() $\left|\lim_{N\to\infty}\int_{\lambda\in(\!-1,0]}\sum_{k=1}^{\infty}\mathbf{1}_{k\leq N}(k) \left(\frac{N-k}{N}\right)\lambda^k\mathcal{E}_{f,\mathcal{P}}(\mathrm{d}\lambda)\right| =\left|\int_{\lambda\in(\!-1,0]}\frac{\lambda}{1-\lambda}\mathcal{E}_{f,\mathcal{P}}(\mathrm{d}\lambda)\right|<\infty$
$\left|\lim_{N\to\infty}\int_{\lambda\in(\!-1,0]}\sum_{k=1}^{\infty}\mathbf{1}_{k\leq N}(k) \left(\frac{N-k}{N}\right)\lambda^k\mathcal{E}_{f,\mathcal{P}}(\mathrm{d}\lambda)\right| =\left|\int_{\lambda\in(\!-1,0]}\frac{\lambda}{1-\lambda}\mathcal{E}_{f,\mathcal{P}}(\mathrm{d}\lambda)\right|<\infty$
and
![]() $\left|\lim_{N\to\infty}\sum_{k=1}^{\infty}\mathbf{1}_{k\leq N}(k) \left(\frac{N-k}{N}\right)\mathcal{E}_{f,\mathcal{P}}(\{-1\})\right| =\left|\left(\frac{-1}{2}\right)\mathcal{E}_{f,\mathcal{P}}(\{-1\})\right| <\infty$
.
$\left|\lim_{N\to\infty}\sum_{k=1}^{\infty}\mathbf{1}_{k\leq N}(k) \left(\frac{N-k}{N}\right)\mathcal{E}_{f,\mathcal{P}}(\{-1\})\right| =\left|\left(\frac{-1}{2}\right)\mathcal{E}_{f,\mathcal{P}}(\{-1\})\right| <\infty$
.
So, denoting
![]() $H(N,k):=\mathbf{1}_{k\leq N}(k)\left(\frac{N-k}{N}\right)$
, by (5), (6), and (7), we have
$H(N,k):=\mathbf{1}_{k\leq N}(k)\left(\frac{N-k}{N}\right)$
, by (5), (6), and (7), we have
 \begin{align*} &\lim_{N\to\infty}\left[\int_{\lambda\in[\!-1,1)}\sum_{k=1}^{\infty}\mathbf{1}_{k\leq N}(k)\left(\frac{N-k}{N}\right)\lambda^k\mathcal{E}_{f,\mathcal{P}}(\mathrm{d}\lambda)\right]\\[5pt] &=\lim_{N\to\infty}\left[\sum_{k=1}^{\infty}H(N,k)(\!-1)^k\mathcal{E}_{f,\mathcal{P}}(\{-1\})\right.+\int_{\lambda\in(\!-1,0]}\sum_{k=1}^{\infty}H(N,k)\lambda^k\mathcal{E}_{f,\mathcal{P}}(\mathrm{d}\lambda)\\[5pt] &\qquad\left.+\int_{\lambda\in(0,1)}\sum_{k=1}^{\infty}H(N,k)\lambda^k\mathcal{E}_{f,\mathcal{P}}(\mathrm{d}\lambda)\right]\\[5pt] &=\lim_{N\to\infty}\sum_{k=1}^{\infty}H(N,k)(\!-1)^k\mathcal{E}_{f,\mathcal{P}}(\{-1\})+\lim_{N\to\infty}\int_{\lambda\in(\!-1,0]}\sum_{k=1}^{\infty}H(N,k)\lambda^k\mathcal{E}_{f,\mathcal{P}}(\mathrm{d}\lambda)\\[5pt] &\qquad+\lim_{N\to\infty}\int_{\lambda\in(0,1)}\sum_{k=1}^{\infty}H(N,k)\lambda^k\mathcal{E}_{f,\mathcal{P}}(\mathrm{d}\lambda)\end{align*}
\begin{align*} &\lim_{N\to\infty}\left[\int_{\lambda\in[\!-1,1)}\sum_{k=1}^{\infty}\mathbf{1}_{k\leq N}(k)\left(\frac{N-k}{N}\right)\lambda^k\mathcal{E}_{f,\mathcal{P}}(\mathrm{d}\lambda)\right]\\[5pt] &=\lim_{N\to\infty}\left[\sum_{k=1}^{\infty}H(N,k)(\!-1)^k\mathcal{E}_{f,\mathcal{P}}(\{-1\})\right.+\int_{\lambda\in(\!-1,0]}\sum_{k=1}^{\infty}H(N,k)\lambda^k\mathcal{E}_{f,\mathcal{P}}(\mathrm{d}\lambda)\\[5pt] &\qquad\left.+\int_{\lambda\in(0,1)}\sum_{k=1}^{\infty}H(N,k)\lambda^k\mathcal{E}_{f,\mathcal{P}}(\mathrm{d}\lambda)\right]\\[5pt] &=\lim_{N\to\infty}\sum_{k=1}^{\infty}H(N,k)(\!-1)^k\mathcal{E}_{f,\mathcal{P}}(\{-1\})+\lim_{N\to\infty}\int_{\lambda\in(\!-1,0]}\sum_{k=1}^{\infty}H(N,k)\lambda^k\mathcal{E}_{f,\mathcal{P}}(\mathrm{d}\lambda)\\[5pt] &\qquad+\lim_{N\to\infty}\int_{\lambda\in(0,1)}\sum_{k=1}^{\infty}H(N,k)\lambda^k\mathcal{E}_{f,\mathcal{P}}(\mathrm{d}\lambda)\end{align*}
 \begin{align*} &=\left(\frac{\lambda}{1-\lambda}\right)\mathcal{E}_{f,\mathcal{P}}(\{\lambda\})|_{\lambda=-1}+\int_{\lambda\in(\!-1,0]}\frac{\lambda}{1-\lambda}\mathcal{E}_{f,\mathcal{P}}(\mathrm{d}\lambda)+\int_{\lambda\in(0,1)}\frac{\lambda}{1-\lambda}\mathcal{E}_{f,\mathcal{P}}(\mathrm{d}\lambda)\\ &=\int_{\lambda\in[\!-1,1)}\frac{\lambda}{1-\lambda}\mathcal{E}_{f,\mathcal{P}}(\mathrm{d}\lambda). \end{align*}
\begin{align*} &=\left(\frac{\lambda}{1-\lambda}\right)\mathcal{E}_{f,\mathcal{P}}(\{\lambda\})|_{\lambda=-1}+\int_{\lambda\in(\!-1,0]}\frac{\lambda}{1-\lambda}\mathcal{E}_{f,\mathcal{P}}(\mathrm{d}\lambda)+\int_{\lambda\in(0,1)}\frac{\lambda}{1-\lambda}\mathcal{E}_{f,\mathcal{P}}(\mathrm{d}\lambda)\\ &=\int_{\lambda\in[\!-1,1)}\frac{\lambda}{1-\lambda}\mathcal{E}_{f,\mathcal{P}}(\mathrm{d}\lambda). \end{align*}
Plugging this into (4), and as
![]() $\mathcal{E}_{f,\mathcal{P}}(\{1\})=0$
by Lemma 3.1, we have
$\mathcal{E}_{f,\mathcal{P}}(\{1\})=0$
by Lemma 3.1, we have
 \begin{align*} v(\,f,P) &=\left\lVert f\right\rVert^2+2\lim_{N\to\infty}\left[\int_{\lambda\in\sigma(\mathcal{P})} \sum_{k=1}^{\infty} \mathbf{1}_{k\leq N}(k)\left(\frac{N-k}{N}\right)\lambda^k\mathcal{E}_{f,\mathcal{P}}(\mathrm{d}\lambda)\right]\\ &=\int_{\lambda\in[\!-1,1)}\mathcal{E}_{f,\mathcal{P}}(\mathrm{d}\lambda)+2\int_{\lambda\in[\!-1,1)} \frac{\lambda}{1-\lambda}\mathcal{E}_{f,\mathcal{P}}(\mathrm{d}\lambda)\\ &=\int_{\lambda\in[\!-1,1)}\frac{1+\lambda}{1-\lambda}\mathcal{E}_{f,\mathcal{P}}(\mathrm{d}\lambda). \end{align*}
\begin{align*} v(\,f,P) &=\left\lVert f\right\rVert^2+2\lim_{N\to\infty}\left[\int_{\lambda\in\sigma(\mathcal{P})} \sum_{k=1}^{\infty} \mathbf{1}_{k\leq N}(k)\left(\frac{N-k}{N}\right)\lambda^k\mathcal{E}_{f,\mathcal{P}}(\mathrm{d}\lambda)\right]\\ &=\int_{\lambda\in[\!-1,1)}\mathcal{E}_{f,\mathcal{P}}(\mathrm{d}\lambda)+2\int_{\lambda\in[\!-1,1)} \frac{\lambda}{1-\lambda}\mathcal{E}_{f,\mathcal{P}}(\mathrm{d}\lambda)\\ &=\int_{\lambda\in[\!-1,1)}\frac{1+\lambda}{1-\lambda}\mathcal{E}_{f,\mathcal{P}}(\mathrm{d}\lambda). \end{align*}
Lemma 3.1. If P is a
![]() $\varphi$
-irreducible Markov kernel reversible with respect to
$\varphi$
-irreducible Markov kernel reversible with respect to
![]() $\pi$
, then for every
$\pi$
, then for every
![]() $f\in L^2_0(\pi)$
,
$f\in L^2_0(\pi)$
,
![]() $\mathcal{E}_{f,\mathcal{P}}(\{1\})=0$
.
$\mathcal{E}_{f,\mathcal{P}}(\{1\})=0$
.
Proof. As outlined in Lemma 4.7.4 in [Reference Gallegos-Herrada, Ledvinka and Rosenthal10], as P is
![]() $\varphi$
-irreducible, the constant function is the only eigenfunction of
$\varphi$
-irreducible, the constant function is the only eigenfunction of
![]() $\mathcal{P}$
with eigenvalue 1; thus, 1 is not an eigenvalue of
$\mathcal{P}$
with eigenvalue 1; thus, 1 is not an eigenvalue of
![]() $\mathcal{P}$
when we restrict ourselves to
$\mathcal{P}$
when we restrict ourselves to
![]() $L^2_0(\pi)$
.
$L^2_0(\pi)$
.
As seen in Theorem 12.29 (b) in [Reference Rudin24], for every normal bounded operator T on a Hilbert space, if
![]() $\lambda\in\mathbf{C}$
is not an eigenvalue of T then
$\lambda\in\mathbf{C}$
is not an eigenvalue of T then
![]() $\mathcal{E}_T(\{\lambda\})=0$
. As P is reversible with respect to
$\mathcal{E}_T(\{\lambda\})=0$
. As P is reversible with respect to
![]() $\pi$
,
$\pi$
,
![]() $\mathcal{P}$
is self-adjoint and thus also normal.
$\mathcal{P}$
is self-adjoint and thus also normal.
So applying the above theorem to
![]() $\mathcal{P}$
, as
$\mathcal{P}$
, as
![]() $1\in\mathbf{C}$
is not an eigenvalue of
$1\in\mathbf{C}$
is not an eigenvalue of
![]() $\mathcal{P}$
, we have
$\mathcal{P}$
, we have
![]() $\mathcal{E}_{\mathcal{P}}(\{1\})=0$
. Thus, for every
$\mathcal{E}_{\mathcal{P}}(\{1\})=0$
. Thus, for every
![]() $f\in L^2_0(\pi)$
,
$f\in L^2_0(\pi)$
,
![]() $\mathcal{E}_{f,\mathcal{P}}(\{1\})=\langle f,\mathcal{E}_{\mathcal{P}}(\{1\})f\rangle= \langle f,0\rangle=0$
.
$\mathcal{E}_{f,\mathcal{P}}(\{1\})=\langle f,\mathcal{E}_{\mathcal{P}}(\{1\})f\rangle= \langle f,0\rangle=0$
.
We now show that if P is aperiodic, then
![]() $-1$
cannot be an eigenvalue of
$-1$
cannot be an eigenvalue of
![]() $\mathcal{P}$
.
$\mathcal{P}$
.
Proposition 3.1. Let P be a Markov kernel reversible with respect to
![]() $\pi$
. If P is aperiodic then
$\pi$
. If P is aperiodic then
![]() $-1$
is not an eigenvalue of
$-1$
is not an eigenvalue of
![]() $\mathcal{P}:L^2_0(\pi)\to L^2_0(\pi)$
.
$\mathcal{P}:L^2_0(\pi)\to L^2_0(\pi)$
.
Proof. We show the contrapositive. That is, we assume that
![]() $-1$
is an eigenvalue of
$-1$
is an eigenvalue of
![]() $\mathcal{P}$
, and show that P is not aperiodic, i.e. is periodic.
$\mathcal{P}$
, and show that P is not aperiodic, i.e. is periodic.
Let
![]() $f\in L^2_0(\pi)$
be an eigenfunction of
$f\in L^2_0(\pi)$
be an eigenfunction of
![]() $\mathcal{P}$
with eigenvalue
$\mathcal{P}$
with eigenvalue
![]() $-1$
. As
$-1$
. As
![]() $\mathcal{P}$
is self-adjoint (as P is reversible), we can assume that f is real-valued. Let
$\mathcal{P}$
is self-adjoint (as P is reversible), we can assume that f is real-valued. Let
![]() $\mathcal{X}_1=\{x\in\mathbf{X}:f(x)>0\}=f^{-1}((0,\infty))$
and
$\mathcal{X}_1=\{x\in\mathbf{X}:f(x)>0\}=f^{-1}((0,\infty))$
and
![]() $\mathcal{X}_2=\{x\in\mathbf{X}:f(x)<0\}=f^{-1}((-\infty,0))$
. As f is
$\mathcal{X}_2=\{x\in\mathbf{X}:f(x)<0\}=f^{-1}((-\infty,0))$
. As f is
![]() $(\mathcal{F},\mathcal{B}(\mathbf{R}))$
-measurable, where
$(\mathcal{F},\mathcal{B}(\mathbf{R}))$
-measurable, where
![]() $\mathcal{B}(\mathbf{R})$
is the Borel
$\mathcal{B}(\mathbf{R})$
is the Borel
![]() $\sigma$
-field on
$\sigma$
-field on
![]() $\mathbf{R}$
,
$\mathbf{R}$
,
![]() $\mathcal{X}_1,\mathcal{X}_2\in\mathcal{F}$
.
$\mathcal{X}_1,\mathcal{X}_2\in\mathcal{F}$
.
As f is an eigenfunction,
![]() $f\neq0$
$f\neq0$
![]() $\pi$
-a.e. As
$\pi$
-a.e. As
![]() $f\in L^2_0(\pi)$
,
$f\in L^2_0(\pi)$
,
So the above combined with the fact that
![]() $f\neq0$
$f\neq0$
![]() $\pi$
-a.e. gives us that
$\pi$
-a.e. gives us that
![]() $\pi(\mathcal{X}_1),\pi(\mathcal{X}_2)>0$
.
$\pi(\mathcal{X}_1),\pi(\mathcal{X}_2)>0$
.
So, as
![]() $\mathcal{P} f=-f$
for
$\mathcal{P} f=-f$
for
![]() $\pi$
-a.e.
$\pi$
-a.e.
![]() $x\in\mathbf{X}$
and P is reversible with respect to
$x\in\mathbf{X}$
and P is reversible with respect to
![]() $\pi$
,
$\pi$
,
Similarly,
![]() $\int_{\mathbf{X}}f(x)P(x,\mathcal{X}_1)\pi(\mathrm{d}x)=\int_{\mathcal{X}_2}f(x)\pi(\mathrm{d}x)$
.
$\int_{\mathbf{X}}f(x)P(x,\mathcal{X}_1)\pi(\mathrm{d}x)=\int_{\mathcal{X}_2}f(x)\pi(\mathrm{d}x)$
.
We now claim that P is periodic with respect to
![]() $\mathcal{X}_1$
and
$\mathcal{X}_1$
and
![]() $\mathcal{X}_2$
. So assume for a contradiction there exists
$\mathcal{X}_2$
. So assume for a contradiction there exists
![]() $E\in\mathcal{F}$
such that
$E\in\mathcal{F}$
such that
![]() $\pi(E)>0$
,
$\pi(E)>0$
,
![]() $E\subseteq\mathcal{X}_1$
and for every
$E\subseteq\mathcal{X}_1$
and for every
![]() $x\in E$
,
$x\in E$
,
![]() $P(x,\mathcal{X}_2)<1$
. Then by the definition of
$P(x,\mathcal{X}_2)<1$
. Then by the definition of
![]() $\mathcal{X}_2$
,
$\mathcal{X}_2$
,
![]() $\int_{\mathbf{X}}f(x)P(x,\mathcal{X}_2)\pi(\mathrm{d}x)\:=\:\int_{\mathcal{X}_1}f(x)\pi(\mathrm{d}x) \:>\:\int_{\mathcal{X}_1}f(x)P(x,\mathcal{X}_2)\pi(\mathrm{d}x) $
$\int_{\mathbf{X}}f(x)P(x,\mathcal{X}_2)\pi(\mathrm{d}x)\:=\:\int_{\mathcal{X}_1}f(x)\pi(\mathrm{d}x) \:>\:\int_{\mathcal{X}_1}f(x)P(x,\mathcal{X}_2)\pi(\mathrm{d}x) $
![]() $\quad\geq\:\int_{\mathbf{X}}f(x)P(x,\mathcal{X}_2)\pi(\mathrm{d}x)$
, a clear contradiction.
$\quad\geq\:\int_{\mathbf{X}}f(x)P(x,\mathcal{X}_2)\pi(\mathrm{d}x)$
, a clear contradiction.
So for
![]() $\pi$
-a.e.
$\pi$
-a.e.
![]() $x\in\mathcal{X}_1$
,
$x\in\mathcal{X}_1$
,
![]() $P(x,\mathcal{X}_2)=1$
. Similarly, for
$P(x,\mathcal{X}_2)=1$
. Similarly, for
![]() $\pi$
-a.e.
$\pi$
-a.e.
![]() $x\in\mathcal{X}_2$
,
$x\in\mathcal{X}_2$
,
![]() $P(x,\mathcal{X}_1)=1$
.
$P(x,\mathcal{X}_1)=1$
.
Thus, P is periodic with period
![]() $d\geq2$
.
$d\geq2$
.
Proposition 3.1, combined with Theorem 3.1, gives us a characterization of v( f, P) as sums of autocovariances,
![]() $\gamma_k$
(recall from Section 2.1), when P is aperiodic (see [Reference Geyer11–Reference Jones13]). Although this characterization will not be used in this paper, it is perhaps more common and easier to interpret from a statistical point of view.
$\gamma_k$
(recall from Section 2.1), when P is aperiodic (see [Reference Geyer11–Reference Jones13]). Although this characterization will not be used in this paper, it is perhaps more common and easier to interpret from a statistical point of view.
Proposition 3.2. If P is an aperiodic
![]() $\varphi$
-irreducible Markov kernel reversible with respect to
$\varphi$
-irreducible Markov kernel reversible with respect to
![]() $\pi$
, then for every
$\pi$
, then for every
![]() $f\in L^2_0(\pi)$
,
$f\in L^2_0(\pi)$
,
Remark 3.1. Even if P is periodic, Proposition 3.2 is still true for all
![]() $f\in L^2_0(\pi)$
that are perpendicular to the eigenfunctions of
$f\in L^2_0(\pi)$
that are perpendicular to the eigenfunctions of
![]() $\mathcal{P}$
with eigenvalue
$\mathcal{P}$
with eigenvalue
![]() $-1$
. (This ensures
$-1$
. (This ensures
![]() $\mathcal{E}_{f,\mathcal{P}}(\{-1\})=0$
.)
$\mathcal{E}_{f,\mathcal{P}}(\{-1\})=0$
.)
Proof. Let
![]() $f\in L^2_0(\pi)$
. By Proposition 3.1,
$f\in L^2_0(\pi)$
. By Proposition 3.1,
![]() $-1$
is not an eigenvalue of
$-1$
is not an eigenvalue of
![]() $\mathcal{P}$
. So, just as in the proof of Lemma 3.1, again by Theorem 12.29 (b) in [Reference Rudin24], as
$\mathcal{P}$
. So, just as in the proof of Lemma 3.1, again by Theorem 12.29 (b) in [Reference Rudin24], as
![]() $\mathcal{P}$
is self-adjoint and thus normal,
$\mathcal{P}$
is self-adjoint and thus normal,
![]() $\mathcal{E}_{f,\mathcal{P}}(\{-1\})=0$
. So by Theorem 3.1,
$\mathcal{E}_{f,\mathcal{P}}(\{-1\})=0$
. So by Theorem 3.1,
![]() $v(\,f,P)=\int_{\lambda\in[\!-1,1)}\frac{1+\lambda}{1-\lambda} \mathcal{E}_{f,\mathcal{P}}(\mathrm{d}\lambda)=\left\lVert f\right\rVert^2+2\int_{\lambda\in(\!-1,1)}\frac{\lambda}{1-\lambda}\mathcal{E}_{f,\mathcal{P}}(\mathrm{d}\lambda)$
.
$v(\,f,P)=\int_{\lambda\in[\!-1,1)}\frac{1+\lambda}{1-\lambda} \mathcal{E}_{f,\mathcal{P}}(\mathrm{d}\lambda)=\left\lVert f\right\rVert^2+2\int_{\lambda\in(\!-1,1)}\frac{\lambda}{1-\lambda}\mathcal{E}_{f,\mathcal{P}}(\mathrm{d}\lambda)$
.
Recalling the geometric series
![]() $\sum_{k=1}^{\infty}\lambda^k=\frac{\lambda}{1-\lambda}$
for
$\sum_{k=1}^{\infty}\lambda^k=\frac{\lambda}{1-\lambda}$
for
![]() $\lambda\in(\!-1,1)$
, by the monotone convergence theorem for
$\lambda\in(\!-1,1)$
, by the monotone convergence theorem for
![]() $\lambda\in(0,1)$
and by the dominated convergence theorem for
$\lambda\in(0,1)$
and by the dominated convergence theorem for
![]() $\lambda\in(\!-1,0]$
, we have
$\lambda\in(\!-1,0]$
, we have
So the asymptotic variance becomes
![]() $v(\,f,P)=\left\lVert f\right\rVert^2+2\int_{\lambda\in(\!-1,1)} \frac{\lambda}{1-\lambda}\mathcal{E}_{f,\mathcal{P}}(\mathrm{d}\lambda)=\left\lVert f\right\rVert^2+2\sum_{k=1}^{\infty} \int_{\lambda\in(\!-1,1)}\lambda^k\mathcal{E}_{f,\mathcal{P}}(\mathrm{d}\lambda)=\left\lVert f\right\rVert^2+2\sum_{k=1}^{\infty} \langle f,\mathcal{P}^kf\rangle=\gamma_0+2\sum_{k=1}^{\infty}\gamma_k$
, as
$v(\,f,P)=\left\lVert f\right\rVert^2+2\int_{\lambda\in(\!-1,1)} \frac{\lambda}{1-\lambda}\mathcal{E}_{f,\mathcal{P}}(\mathrm{d}\lambda)=\left\lVert f\right\rVert^2+2\sum_{k=1}^{\infty} \int_{\lambda\in(\!-1,1)}\lambda^k\mathcal{E}_{f,\mathcal{P}}(\mathrm{d}\lambda)=\left\lVert f\right\rVert^2+2\sum_{k=1}^{\infty} \langle f,\mathcal{P}^kf\rangle=\gamma_0+2\sum_{k=1}^{\infty}\gamma_k$
, as
![]() $\mathbf{E}_{\pi}(f)=0$
.
$\mathbf{E}_{\pi}(f)=0$
.
Remark 3.2. In the non-reversible case, it is not guaranteed that the asymptotic variance exists (either a real number or infinite). However, the existence of the ‘
![]() $\lambda$
-asymptotic variance’,
$\lambda$
-asymptotic variance’,
![]() $v_{\lambda}(\,f,P)\,:\!=\,\left\lVert f\right\rVert^2+2\sum_{k=1}^{\infty} \lambda^k\langle f,\mathcal{P}^kf\rangle$
for
$v_{\lambda}(\,f,P)\,:\!=\,\left\lVert f\right\rVert^2+2\sum_{k=1}^{\infty} \lambda^k\langle f,\mathcal{P}^kf\rangle$
for
![]() $\lambda\in[0,1)$
(where
$\lambda\in[0,1)$
(where
![]() $\lambda$
is simply a parameter, not an element of the spectrum of
$\lambda$
is simply a parameter, not an element of the spectrum of
![]() $\mathcal{P}$
), is guaranteed to exist (although it may be infinite). As such, progress has been made comparing the
$\mathcal{P}$
), is guaranteed to exist (although it may be infinite). As such, progress has been made comparing the
![]() $\lambda$
-asymptotic variance of non-reversible kernels, rather than the asymptotic variance, as in [Reference Andrieu and Livingstone1], and we are left with the problem of showing
$\lambda$
-asymptotic variance of non-reversible kernels, rather than the asymptotic variance, as in [Reference Andrieu and Livingstone1], and we are left with the problem of showing
![]() $v_{\lambda}(f,P)$
converges to v( f, P), i.e.
$v_{\lambda}(f,P)$
converges to v( f, P), i.e.
![]() $\lim_{\lambda\to1^-}v_{\lambda}(f,P)=v(\,f,P)$
. Noting that as in [Reference Tierney27] we can write
$\lim_{\lambda\to1^-}v_{\lambda}(f,P)=v(\,f,P)$
. Noting that as in [Reference Tierney27] we can write
![]() $v_{\lambda}(f,P)=\langle f,\left(\mathcal{I}-\lambda\mathcal{P}\right)^{-1}\left(\mathcal{I}-\lambda\mathcal{P}\right)f\rangle$
, an easy application of the spectral theorem and the dominated and monotone convergence theorems as we have done in the proofs of Theorem 3.1 and Proposition 3.2 shows that
$v_{\lambda}(f,P)=\langle f,\left(\mathcal{I}-\lambda\mathcal{P}\right)^{-1}\left(\mathcal{I}-\lambda\mathcal{P}\right)f\rangle$
, an easy application of the spectral theorem and the dominated and monotone convergence theorems as we have done in the proofs of Theorem 3.1 and Proposition 3.2 shows that
![]() $\lim_{\lambda\to1^-}v_{\lambda}(f,P)=v(\,f,P)$
whenever P is
$\lim_{\lambda\to1^-}v_{\lambda}(f,P)=v(\,f,P)$
whenever P is
![]() $\varphi$
-irreducible and reversible (not necessarily aperiodic).
$\varphi$
-irreducible and reversible (not necessarily aperiodic).
4. Efficiency Dominance Equivalence
In this section, we prove our most useful equivalent condition for efficiency dominance for reversible Markov kernels first introduced in [Reference Mira and Geyer18]. We use basic functional analysis to provide a simpler proof that stays clear of overly technical arguments. We then use this equivalent condition to show how reversible antithetic Markov kernels are more efficient than i.i.d. sampling, and show that efficiency dominance is a partial ordering on reversible kernels.
We state the equivalent condition theorem here, and then cover a brief example before introducing the lemmas we need from functional analysis and proving each direction of the equivalence. We prove said lemmas in Section 7.
Theorem 4.1. If P and Q are Markov kernels reversible with respect to
![]() $\pi$
, then P efficiency-dominates Q if and only if
$\pi$
, then P efficiency-dominates Q if and only if
Example 4.1. (DA algorithms and their sandwich variants.) Say we want to estimate samples from the probability density
![]() $f_X:\mathbf{X}\to[0,\infty)$
on
$f_X:\mathbf{X}\to[0,\infty)$
on
![]() $(\mathbf{X},\mathcal{X},\mu)$
. If we have access to conditional densities
$(\mathbf{X},\mathcal{X},\mu)$
. If we have access to conditional densities
![]() $f_{X|Y}(\cdot|y)$
and
$f_{X|Y}(\cdot|y)$
and
![]() $f_{Y|X}(\cdot|x)$
on the spaces
$f_{Y|X}(\cdot|x)$
on the spaces
![]() $(\mathbf{X},\mathcal{X},\mu)$
and another space
$(\mathbf{X},\mathcal{X},\mu)$
and another space
![]() $(\mathbf{Y},\mathcal{Y},\nu)$
, respectively (where there exists a density
$(\mathbf{Y},\mathcal{Y},\nu)$
, respectively (where there exists a density
![]() $f\,:\,\mathbf{X}\times\mathbf{Y}\to[0,\infty)$
with
$f\,:\,\mathbf{X}\times\mathbf{Y}\to[0,\infty)$
with
![]() $f_X(x)=\int_{\mathbf{Y}}f(x,y)\nu(\mathrm{d}y)$
), then we can implement a DA MCMC algorithm to estimate from
$f_X(x)=\int_{\mathbf{Y}}f(x,y)\nu(\mathrm{d}y)$
), then we can implement a DA MCMC algorithm to estimate from
![]() $f_X$
.
$f_X$
.
The DA MCMC algorithm works as follows. If
![]() $\{X_k\}_{k=0}^{\infty}$
is our Markov chain, after starting
$\{X_k\}_{k=0}^{\infty}$
is our Markov chain, after starting
![]() $X_0$
according to some initial distribution, given
$X_0$
according to some initial distribution, given
![]() $X_k=x\in\mathbf{X}$
, we sample from
$X_k=x\in\mathbf{X}$
, we sample from
![]() $f_{Y|X}(\cdot|x)$
to get a
$f_{Y|X}(\cdot|x)$
to get a
![]() $y\in\mathbf{Y}$
, and then sample again from
$y\in\mathbf{Y}$
, and then sample again from
![]() $f_{X|Y}(\cdot|y)$
to get our value
$f_{X|Y}(\cdot|y)$
to get our value
![]() $x'\in\mathbf{X}$
, and set
$x'\in\mathbf{X}$
, and set
![]() $X_{k+1}=x'$
. The Markov kernel according to this algorithm is
$X_{k+1}=x'$
. The Markov kernel according to this algorithm is
![]() $P_{\mathrm{DA}}(x,\mathrm{d}x')=\int_{\mathbf{Y}}f_{X|Y}(x'|y)f_{Y|X}(y|x)\nu(\mathrm{d}y)\mu(\mathrm{d}x')$
.
$P_{\mathrm{DA}}(x,\mathrm{d}x')=\int_{\mathbf{Y}}f_{X|Y}(x'|y)f_{Y|X}(y|x)\nu(\mathrm{d}y)\mu(\mathrm{d}x')$
.
Often the DA algorithm can be inefficient, and we can improve its performance by adding a middle step. Given a Markov kernel R on
![]() $(\mathbf{Y},\mathcal{Y})$
, after we have our sample
$(\mathbf{Y},\mathcal{Y})$
, after we have our sample
![]() $y\in\mathbf{Y}$
by sampling from
$y\in\mathbf{Y}$
by sampling from
![]() $f_{Y|X}(\cdot|x)$
, we sample from
$f_{Y|X}(\cdot|x)$
, we sample from
![]() $R(y,\cdot)$
to get another sample in
$R(y,\cdot)$
to get another sample in
![]() $\mathbf{Y}$
,
$\mathbf{Y}$
,
![]() $y'\in\mathbf{Y}$
, and then use this value to finish the loop by sampling from
$y'\in\mathbf{Y}$
, and then use this value to finish the loop by sampling from
![]() $f_{X|Y}(\cdot|y')$
. This algorithm is dubbed the sandwich DA algorithm, as the middle step of sampling from
$f_{X|Y}(\cdot|y')$
. This algorithm is dubbed the sandwich DA algorithm, as the middle step of sampling from
![]() $R(y,\cdot)$
is ‘sandwiched’ between the outer steps of the DA algorithm. This MCMC algorithm has Markov kernel
$R(y,\cdot)$
is ‘sandwiched’ between the outer steps of the DA algorithm. This MCMC algorithm has Markov kernel
![]() $P_{\mathrm{S}}(x,\mathrm{d}x')=\iint_{\mathbf{Y}}f_{X|Y}(x'|y')R(y,\mathrm{d}y')f_{Y|X}(y|x)\nu(\mathrm{d}y)\mu(\mathrm{d}x')$
.
$P_{\mathrm{S}}(x,\mathrm{d}x')=\iint_{\mathbf{Y}}f_{X|Y}(x'|y')R(y,\mathrm{d}y')f_{Y|X}(y|x)\nu(\mathrm{d}y)\mu(\mathrm{d}x')$
.
The following diagram illustrates the DA and sandwich DA MCMC algorithms, with the DA algorithm on the left and the sandwich DA algorithm on the right.

This general form of the sandwich DA algorithm was first introduced in [Reference Khare and Hobert14]. For a more detailed analysis and background on the comparison between the DA and sandwich DA algorithms, see [Reference Khare and Hobert14]. We follow the analysis there to show here that under suitable conditions, the sandwich DA algorithm efficiency dominates the DA algorithm.
Using the definition of conditional densities, it is not hard to see that
![]() $P_{\mathrm{DA}}(x,\mathrm{d}x')f_X(x)\mu(\mathrm{d}x)=P_{\mathrm{DA}}(x',\mathrm{d}x)f_X(x')\mu(\mathrm{d}x')$
, i.e. that the DA algorithm is reversible with respect to
$P_{\mathrm{DA}}(x,\mathrm{d}x')f_X(x)\mu(\mathrm{d}x)=P_{\mathrm{DA}}(x',\mathrm{d}x)f_X(x')\mu(\mathrm{d}x')$
, i.e. that the DA algorithm is reversible with respect to
![]() $f_X\mu$
. If the Markov kernel R is reversible with respect to
$f_X\mu$
. If the Markov kernel R is reversible with respect to
![]() $f_Y\nu$
, a similar argument will show that the sandwich DA algorithm is reversible with respect to
$f_Y\nu$
, a similar argument will show that the sandwich DA algorithm is reversible with respect to
![]() $f_X\mu$
as well.
$f_X\mu$
as well.
We let
![]() $T_X:L^2_0(\mathbf{Y},\mathcal{Y},f_Y\nu)\to L^2_0(\mathbf{X},\mathcal{X},f_X\mu)$
such that
$T_X:L^2_0(\mathbf{Y},\mathcal{Y},f_Y\nu)\to L^2_0(\mathbf{X},\mathcal{X},f_X\mu)$
such that
(where
![]() $L^2_0(f_Y):=L^2_0(\mathbf{Y},\mathcal{Y},f_Y\nu)$
). We similarly define
$L^2_0(f_Y):=L^2_0(\mathbf{Y},\mathcal{Y},f_Y\nu)$
). We similarly define
![]() $T_Y\,:\,L^2_0(f_X)\to L^2_0(f_Y)$
. Then notice that given the DA kernel
$T_Y\,:\,L^2_0(f_X)\to L^2_0(f_Y)$
. Then notice that given the DA kernel
![]() $P_{\mathrm{DA}}$
and the sandwich DA kernel
$P_{\mathrm{DA}}$
and the sandwich DA kernel
![]() $P_{\mathrm{S}}$
, we have
$P_{\mathrm{S}}$
, we have
A common condition on the Markov kernel R is that it is idempotent, i.e.
![]() $\int_{z\in\mathbf{Y}}R(y,dz)R(z,\mathrm{d}y')=R(y,\mathrm{d}y')$
for every
$\int_{z\in\mathbf{Y}}R(y,dz)R(z,\mathrm{d}y')=R(y,\mathrm{d}y')$
for every
![]() $y\in\mathbf{Y}$
, or equivalently,
$y\in\mathbf{Y}$
, or equivalently,
![]() $\mathcal{R}^2=\mathcal{R}$
. So if the sandwich algorithm as given is such that R is reversible and idempotent, then notice that by (9), for every
$\mathcal{R}^2=\mathcal{R}$
. So if the sandwich algorithm as given is such that R is reversible and idempotent, then notice that by (9), for every
![]() $g\in L^2_0(f_X)$
,
$g\in L^2_0(f_X)$
,
Thus
![]() $\mathcal{P}_{\mathrm{S}}$
and
$\mathcal{P}_{\mathrm{S}}$
and
![]() $\mathcal{P}_{\mathrm{DA}}$
satisfy (8), and thus by Theorem 4.1 the sandwich DA algorithm efficiency-dominates the DA algorithm.
$\mathcal{P}_{\mathrm{DA}}$
satisfy (8), and thus by Theorem 4.1 the sandwich DA algorithm efficiency-dominates the DA algorithm.
To prove the ‘if’ direction of Theorem 4.1, we use Lemma 4.1, which is a generalization of some results found in Chapter V in [Reference Bhatia5] from finite-dimensional vector spaces to general Hilbert spaces. The finite-dimensional version of Lemma 4.1 is also presented in [Reference Neal and Rosenthal20] as Lemma 24.
Lemma 4.1. If T and N are self-adjoint bounded linear operators on a Hilbert space
![]() $\mathbf{H}$
such that
$\mathbf{H}$
such that
![]() $\sigma(T),\sigma(N)\subseteq(0,\infty)$
, then
$\sigma(T),\sigma(N)\subseteq(0,\infty)$
, then
![]() $\langle f,Tf\rangle\leq\langle f,Nf\rangle$
for every
$\langle f,Tf\rangle\leq\langle f,Nf\rangle$
for every
![]() $f\in\mathbf{H}$
if and only if
$f\in\mathbf{H}$
if and only if
![]() $\langle f,T^{-1}f\rangle\geq\langle f,N^{-1}f\rangle$
for every
$\langle f,T^{-1}f\rangle\geq\langle f,N^{-1}f\rangle$
for every
![]() $f\in\mathbf{H}$
.
$f\in\mathbf{H}$
.
Lemma 4.1 is proven in Section 7.1, where we discuss the differences in Lemma 4.1 between finite-dimensional vector spaces (as shown in [Reference Neal and Rosenthal20]) and general Hilbert spaces.
We now prove the ‘if’ direction of Theorem 4.1 with the help of Lemma 4.1. Notably, this proof stays clear of any results about monotone operator functions (in contrast to [Reference Mira and Geyer18], which uses results from [Reference Bendat and Sherman4]), to be simpler and much more accessible.
Proof of ‘if’ direction of Theorem 4.1. We start with the case that both P and Q are
![]() $\varphi$
-irreducible. So, say
$\varphi$
-irreducible. So, say
![]() $\mathcal{P}$
and
$\mathcal{P}$
and
![]() $\mathcal{Q}$
satisfy (8). For every
$\mathcal{Q}$
satisfy (8). For every
![]() $\eta\in[0,1)$
, let
$\eta\in[0,1)$
, let
![]() $T_{\mathcal{P},\eta}=\mathcal{I}-\eta\mathcal{P}$
and
$T_{\mathcal{P},\eta}=\mathcal{I}-\eta\mathcal{P}$
and
![]() $T_{\mathcal{Q},\eta}=\mathcal{I}-\eta\mathcal{Q}$
. Then as
$T_{\mathcal{Q},\eta}=\mathcal{I}-\eta\mathcal{Q}$
. Then as
![]() $\left\lVert\mathcal{P}\right\rVert,\left\lVert\mathcal{Q}\right\rVert\leq1$
, by the Cauchy–Schwarz inequality, for every
$\left\lVert\mathcal{P}\right\rVert,\left\lVert\mathcal{Q}\right\rVert\leq1$
, by the Cauchy–Schwarz inequality, for every
![]() $f\in L^2_0(\pi)$
,
$f\in L^2_0(\pi)$
,
![]() $\left|\langle f,\mathcal{P} f\rangle\right|\leq\left\lVert f\right\rVert^2$
and
$\left|\langle f,\mathcal{P} f\rangle\right|\leq\left\lVert f\right\rVert^2$
and
![]() $\left|\langle f,\mathcal{Q} f\rangle\right|\leq\left\lVert f\right\rVert^2$
. So again by the Cauchy–Schwarz inequality, for every
$\left|\langle f,\mathcal{Q} f\rangle\right|\leq\left\lVert f\right\rVert^2$
. So again by the Cauchy–Schwarz inequality, for every
![]() $f\in L^2_0(\pi)$
,
$f\in L^2_0(\pi)$
,
 \begin{align*} \left\lVert T_{\mathcal{P},\eta}f\right\rVert\left\lVert f\right\rVert &\geq\left|\langle T_{\mathcal{P},\eta}f,f\rangle\right|\\ &=\left|\left\lVert f\right\rVert^2-\eta\langle f,\mathcal{P} f\rangle\right|\\ &\geq\left|1-\eta\right|\left\lVert f\right\rVert^2. \end{align*}
\begin{align*} \left\lVert T_{\mathcal{P},\eta}f\right\rVert\left\lVert f\right\rVert &\geq\left|\langle T_{\mathcal{P},\eta}f,f\rangle\right|\\ &=\left|\left\lVert f\right\rVert^2-\eta\langle f,\mathcal{P} f\rangle\right|\\ &\geq\left|1-\eta\right|\left\lVert f\right\rVert^2. \end{align*}
Thus, for every
![]() $f\in L^2_0(\pi)$
,
$f\in L^2_0(\pi)$
,
![]() $\left\lVert T_{\mathcal{P},\eta}f\right\rVert,\left\lVert T_{\mathcal{Q},\eta}f\right\rVert\geq\left|1-\eta\right| \left\lVert f\right\rVert$
. As
$\left\lVert T_{\mathcal{P},\eta}f\right\rVert,\left\lVert T_{\mathcal{Q},\eta}f\right\rVert\geq\left|1-\eta\right| \left\lVert f\right\rVert$
. As
![]() $\eta \in[0,1)$
,
$\eta \in[0,1)$
,
![]() $\left|1-\eta\right|>0$
, and as
$\left|1-\eta\right|>0$
, and as
![]() $T_{\mathcal{P},\eta}$
and
$T_{\mathcal{P},\eta}$
and
![]() $T_{\mathcal{Q},\eta}$
are both normal (as they are self-adjoint),
$T_{\mathcal{Q},\eta}$
are both normal (as they are self-adjoint),
![]() $T_{\mathcal{P},\eta}$
and
$T_{\mathcal{P},\eta}$
and
![]() $T_{\mathcal{Q},\eta}$
are both invertible, in the sense of bounded linear operators, i.e. the inverses of
$T_{\mathcal{Q},\eta}$
are both invertible, in the sense of bounded linear operators, i.e. the inverses of
![]() $T_{\mathcal{P},\eta}$
and
$T_{\mathcal{P},\eta}$
and
![]() $T_{\mathcal{Q},\eta}$
are bounded, and
$T_{\mathcal{Q},\eta}$
are bounded, and
![]() $0\notin\sigma(T_{\mathcal{P},\eta}),\sigma(T_{\mathcal{Q},\eta})$
(by Lemma 7.2).
$0\notin\sigma(T_{\mathcal{P},\eta}),\sigma(T_{\mathcal{Q},\eta})$
(by Lemma 7.2).
As
![]() $\left\lVert\mathcal{P}\right\rVert,\left\lVert\mathcal{Q}\right\rVert\leq1$
and
$\left\lVert\mathcal{P}\right\rVert,\left\lVert\mathcal{Q}\right\rVert\leq1$
and
![]() $\mathcal{P}$
and
$\mathcal{P}$
and
![]() $\mathcal{Q}$
are self-adjoint (as P and Q are reversible),
$\mathcal{Q}$
are self-adjoint (as P and Q are reversible),
![]() $\sigma(\mathcal{P}),\sigma(\mathcal{Q})\subseteq[\!-1,1]$
. Thus, for every
$\sigma(\mathcal{P}),\sigma(\mathcal{Q})\subseteq[\!-1,1]$
. Thus, for every
![]() $\eta\in[0,1)$
,
$\eta\in[0,1)$
,
![]() $\sigma(T_{\mathcal{P},\eta}),\sigma(T_{\mathcal{Q},\eta})\subseteq(0,2) \subseteq(0,\infty)$
.
$\sigma(T_{\mathcal{P},\eta}),\sigma(T_{\mathcal{Q},\eta})\subseteq(0,2) \subseteq(0,\infty)$
.
So for every
![]() $\eta\in[0,1)$
, as
$\eta\in[0,1)$
, as
![]() $T_{\mathcal{P},\eta}$
and
$T_{\mathcal{P},\eta}$
and
![]() $T_{\mathcal{Q},\eta}$
are both self-adjoint, and for every
$T_{\mathcal{Q},\eta}$
are both self-adjoint, and for every
![]() $f\in L^2_0(\pi)$
,
$f\in L^2_0(\pi)$
,
![]() $\langle f,T_{\mathcal{Q},\eta}f\rangle=\left\lVert f\right\rVert^2-\eta\langle f,\mathcal{Q} f\rangle \leq\left\lVert f\right\rVert^2-\eta\langle f,\mathcal{P} f\rangle=\langle f,T_{\mathcal{P},\eta}f\rangle$
, by Lemma 4.1,
$\langle f,T_{\mathcal{Q},\eta}f\rangle=\left\lVert f\right\rVert^2-\eta\langle f,\mathcal{Q} f\rangle \leq\left\lVert f\right\rVert^2-\eta\langle f,\mathcal{P} f\rangle=\langle f,T_{\mathcal{P},\eta}f\rangle$
, by Lemma 4.1,
![]() $\langle f,T^{-1}_{\mathcal{Q},\eta}f\rangle\geq\langle f,T^{-1}_{\mathcal{P},\eta}f\rangle$
for every
$\langle f,T^{-1}_{\mathcal{Q},\eta}f\rangle\geq\langle f,T^{-1}_{\mathcal{P},\eta}f\rangle$
for every
![]() $f\in L^2_0(\pi)$
.
$f\in L^2_0(\pi)$
.
Notice that for every
![]() $\eta\in[0,1)$
,
$\eta\in[0,1)$
,
![]() $T^{-1}_{\mathcal{P},\eta}=\left(\mathcal{I}-\eta\mathcal{P}\right)\left(\mathcal{I}-\eta\mathcal{P}\right)^{-1} +\eta\mathcal{P}\left(\mathcal{I}-\eta\mathcal{P}\right)^{-1}=\mathcal{I}+\eta\mathcal{P}\left(\mathcal{I}-\eta\mathcal{P}\right)^{-1}$
. So for every
$T^{-1}_{\mathcal{P},\eta}=\left(\mathcal{I}-\eta\mathcal{P}\right)\left(\mathcal{I}-\eta\mathcal{P}\right)^{-1} +\eta\mathcal{P}\left(\mathcal{I}-\eta\mathcal{P}\right)^{-1}=\mathcal{I}+\eta\mathcal{P}\left(\mathcal{I}-\eta\mathcal{P}\right)^{-1}$
. So for every
![]() $f\in L^2_0(\pi)$
,
$f\in L^2_0(\pi)$
,
 \begin{align*} \left\lVert f\right\rVert^2+\eta\langle f,\mathcal{P}\left(\mathcal{I}-\eta\mathcal{P}\right)^{-1}f\rangle &=\langle f,T^{-1}_{\mathcal{P},\eta}f\rangle\\ &\leq\langle f,T^{-1}_{\mathcal{Q},\eta}f\rangle =\left\lVert f\right\rVert^2+\eta\langle f,\mathcal{Q}\left(\mathcal{I}-\eta\mathcal{Q}\right)^{-1}f\rangle, \end{align*}
\begin{align*} \left\lVert f\right\rVert^2+\eta\langle f,\mathcal{P}\left(\mathcal{I}-\eta\mathcal{P}\right)^{-1}f\rangle &=\langle f,T^{-1}_{\mathcal{P},\eta}f\rangle\\ &\leq\langle f,T^{-1}_{\mathcal{Q},\eta}f\rangle =\left\lVert f\right\rVert^2+\eta\langle f,\mathcal{Q}\left(\mathcal{I}-\eta\mathcal{Q}\right)^{-1}f\rangle, \end{align*}
so for every
![]() $f\in L^2_0(\pi)$
,
$f\in L^2_0(\pi)$
,
![]() $\langle f,\mathcal{P}\left(\mathcal{I}-\eta\mathcal{P}\right)^{-1}f\rangle\leq \langle f,\mathcal{Q}\left(\mathcal{I}-\eta\mathcal{Q}\right)^{-1}f\rangle$
.
$\langle f,\mathcal{P}\left(\mathcal{I}-\eta\mathcal{P}\right)^{-1}f\rangle\leq \langle f,\mathcal{Q}\left(\mathcal{I}-\eta\mathcal{Q}\right)^{-1}f\rangle$
.
Thus, by the monotone convergence theorem for
![]() $\lambda\in(0,1)$
and the dominated convergence theorem for
$\lambda\in(0,1)$
and the dominated convergence theorem for
![]() $\lambda\in[\!-1,0]$
, for every
$\lambda\in[\!-1,0]$
, for every
![]() $f\in L^2_0(\pi)$
,
$f\in L^2_0(\pi)$
,
![]() $\lim_{\eta\to1^-}\int_{[\!-1,1)}\frac{\lambda}{1-\eta\lambda}\mathcal{E}_{f,\mathcal{P}}(\mathrm{d}\lambda)= \int_{[\!-1,1)}\frac{\lambda}{1-\lambda}\mathcal{E}_{f,\mathcal{P}}(\mathrm{d}\lambda)$
, and similarly for
$\lim_{\eta\to1^-}\int_{[\!-1,1)}\frac{\lambda}{1-\eta\lambda}\mathcal{E}_{f,\mathcal{P}}(\mathrm{d}\lambda)= \int_{[\!-1,1)}\frac{\lambda}{1-\lambda}\mathcal{E}_{f,\mathcal{P}}(\mathrm{d}\lambda)$
, and similarly for
![]() $\mathcal{Q}$
.
$\mathcal{Q}$
.
As P and Q are
![]() $\varphi$
-irreducible and reversible with respect to
$\varphi$
-irreducible and reversible with respect to
![]() $\pi$
, by Theorem 3.1, for every
$\pi$
, by Theorem 3.1, for every
![]() $f\in L^2_0(\pi)$
,
$f\in L^2_0(\pi)$
,
 \begin{align*} &v(\,f,P) \;=\;\int_{[\!-1,1)}\frac{1+\lambda}{1-\lambda}\mathcal{E}_{f,\mathcal{P}}(\mathrm{d}\lambda) \;=\;\left\lVert f\right\rVert^2+2\int_{[\!-1,1)}\frac{\lambda}{1-\lambda}\mathcal{E}_{f,\mathcal{P}}(\mathrm{d}\lambda)\\ &\;=\;\left\lVert f\right\rVert^2+2\lim_{\eta\to1^-}\int_{[\!-1,1)}\frac{\lambda}{1-\eta\lambda} \mathcal{E}_{f,\mathcal{P}}(\mathrm{d}\lambda) \;=\;\left\lVert f\right\rVert^2+2\lim_{\eta\to1^-}\langle f,\mathcal{P}\left(\mathcal{I}-\eta\mathcal{P}\right)^{-1}f\rangle\\ &\;\leq\;\left\lVert f\right\rVert^2+2\lim_{\eta\to1^-}\langle f,\mathcal{Q}\left(\mathcal{I}-\eta\mathcal{Q}\right)^{-1}f\rangle \;=\;\left\lVert f\right\rVert^2+2\lim_{\eta\to1^-}\int_{[\!-1,1)}\frac{\lambda}{1-\eta\lambda} \mathcal{E}_{f,\mathcal{Q}}(\mathrm{d}\lambda)\\ &\;=\;\left\lVert f\right\rVert^2+2\int_{[\!-1,1)}\frac{\lambda}{1-\lambda}\mathcal{E}_{f,\mathcal{Q}}(\mathrm{d}\lambda) \;=\;\int_{[\!-1,1)}\frac{1+\lambda}{1-\lambda}\mathcal{E}_{f,\mathcal{Q}}(\mathrm{d}\lambda) \;=\;v(\,f,Q). \end{align*}
\begin{align*} &v(\,f,P) \;=\;\int_{[\!-1,1)}\frac{1+\lambda}{1-\lambda}\mathcal{E}_{f,\mathcal{P}}(\mathrm{d}\lambda) \;=\;\left\lVert f\right\rVert^2+2\int_{[\!-1,1)}\frac{\lambda}{1-\lambda}\mathcal{E}_{f,\mathcal{P}}(\mathrm{d}\lambda)\\ &\;=\;\left\lVert f\right\rVert^2+2\lim_{\eta\to1^-}\int_{[\!-1,1)}\frac{\lambda}{1-\eta\lambda} \mathcal{E}_{f,\mathcal{P}}(\mathrm{d}\lambda) \;=\;\left\lVert f\right\rVert^2+2\lim_{\eta\to1^-}\langle f,\mathcal{P}\left(\mathcal{I}-\eta\mathcal{P}\right)^{-1}f\rangle\\ &\;\leq\;\left\lVert f\right\rVert^2+2\lim_{\eta\to1^-}\langle f,\mathcal{Q}\left(\mathcal{I}-\eta\mathcal{Q}\right)^{-1}f\rangle \;=\;\left\lVert f\right\rVert^2+2\lim_{\eta\to1^-}\int_{[\!-1,1)}\frac{\lambda}{1-\eta\lambda} \mathcal{E}_{f,\mathcal{Q}}(\mathrm{d}\lambda)\\ &\;=\;\left\lVert f\right\rVert^2+2\int_{[\!-1,1)}\frac{\lambda}{1-\lambda}\mathcal{E}_{f,\mathcal{Q}}(\mathrm{d}\lambda) \;=\;\int_{[\!-1,1)}\frac{1+\lambda}{1-\lambda}\mathcal{E}_{f,\mathcal{Q}}(\mathrm{d}\lambda) \;=\;v(\,f,Q). \end{align*}
So as
![]() $v(\,f,P)\leq v(\,f,Q)$
for every
$v(\,f,P)\leq v(\,f,Q)$
for every
![]() $f\in L^2_0(\pi)$
,
$f\in L^2_0(\pi)$
,
![]() $v(\,f,P)\leq v(\,f,Q)$
for every
$v(\,f,P)\leq v(\,f,Q)$
for every
![]() $f\in L^2(\pi)$
(see Section 2.1), and thus P efficiency-dominates Q.
$f\in L^2(\pi)$
(see Section 2.1), and thus P efficiency-dominates Q.
The condition that P and Q be
![]() $\varphi$
-irreducible in the above proof can be dropped by our noting a few things.
$\varphi$
-irreducible in the above proof can be dropped by our noting a few things.
-
1. The condition that the Markov kernel P be
 $\varphi$
-irreducible in Theorem 3.1 is only so we have
$\varphi$
-irreducible in Theorem 3.1 is only so we have
 $\mathcal{E}_{f,\mathcal{P}}(\{1\})=0$
. If P is not
$\mathcal{E}_{f,\mathcal{P}}(\{1\})=0$
. If P is not
 $\varphi$
-irreducible, (2) still holds for all
$\varphi$
-irreducible, (2) still holds for all
 $f\in L^2_0(\pi)$
such that
$f\in L^2_0(\pi)$
such that
 $\mathcal{E}_{f,\mathcal{P}}(\{1\})=0$
.
$\mathcal{E}_{f,\mathcal{P}}(\{1\})=0$
. -
2. If P and Q are reversible kernels such that (8) holds, then the eigenspace
 $\mathbf{E}_{\mathcal{P}}(1)\,:\!=\,\{f\in L^2_0(\pi)\,:\,\mathcal{P} f=f\}=\textrm{null}(\mathcal{P}-\mathcal{I})$
of
$\mathbf{E}_{\mathcal{P}}(1)\,:\!=\,\{f\in L^2_0(\pi)\,:\,\mathcal{P} f=f\}=\textrm{null}(\mathcal{P}-\mathcal{I})$
of
 $\mathcal{P}$
with respect to the eigenvalue 1 is necessarily contained in the eigenspace
$\mathcal{P}$
with respect to the eigenvalue 1 is necessarily contained in the eigenspace
 $\mathbf{E}_{\mathcal{Q}}(1)$
of
$\mathbf{E}_{\mathcal{Q}}(1)$
of
 $\mathcal{Q}$
with respect to the eigenvalue 1. For every
$\mathcal{Q}$
with respect to the eigenvalue 1. For every
 $f\in\mathbf{E}_{\mathcal{P}}(1)$
, by (8) and the Cauchy–Schwarz inequality,
$f\in\mathbf{E}_{\mathcal{P}}(1)$
, by (8) and the Cauchy–Schwarz inequality,
 $\left\lVert\mathcal{Q} f\right\rVert=\left\lVert f\right\rVert$
, and as
$\left\lVert\mathcal{Q} f\right\rVert=\left\lVert f\right\rVert$
, and as
 $\mathcal{Q}$
is self-adjoint, it must follow that
$\mathcal{Q}$
is self-adjoint, it must follow that
 $\mathcal{Q} f=f$
, or
$\mathcal{Q} f=f$
, or
 $f\in\mathbf{E}_{\mathcal{Q}}(1)$
.
$f\in\mathbf{E}_{\mathcal{Q}}(1)$
. -
3. As eigenspaces are closed, we can decompose
 $L^2_0(\pi)$
as
$L^2_0(\pi)$
as
 $M\oplus M^{\perp}$
for any eigenspace M, where
$M\oplus M^{\perp}$
for any eigenspace M, where
 $M^{\perp}\,:\!=\,\{f\in L^2_0(\pi)\,:\,f\perp M\}=\{f\in L^2_0(\pi)\,:\,f\perp g,\text{ for every }g\in M\}$
.
$M^{\perp}\,:\!=\,\{f\in L^2_0(\pi)\,:\,f\perp M\}=\{f\in L^2_0(\pi)\,:\,f\perp g,\text{ for every }g\in M\}$
.
With these three facts we prove the general case. If
![]() $f\in L^2_0(\pi)$
such that
$f\in L^2_0(\pi)$
such that
![]() $\mathcal{E}_{f,\mathcal{Q}}(\{1\})\neq0$
, then by fact 3,
$\mathcal{E}_{f,\mathcal{Q}}(\{1\})\neq0$
, then by fact 3,
![]() $f=f_0+g$
for some
$f=f_0+g$
for some
![]() $f_0\in\mathbf{E}_{\mathcal{Q}}(1)$
and
$f_0\in\mathbf{E}_{\mathcal{Q}}(1)$
and
![]() $g\in\mathbf{E}_{\mathcal{Q}}(1)^{\perp}$
. As
$g\in\mathbf{E}_{\mathcal{Q}}(1)^{\perp}$
. As
![]() $\mathcal{Q}$
is self-adjoint, by the Cauchy–Schwarz inequality, for every
$\mathcal{Q}$
is self-adjoint, by the Cauchy–Schwarz inequality, for every
![]() $N\in\mathbf{N}$
,
$N\in\mathbf{N}$
,
 \begin{align} \sum_{k=1}^N\left(\frac{N-k}{N}\right)\langle g,\mathcal{Q}^kg\rangle\;&=\;\left(\frac{N-1}{N}\right)\langle g,\mathcal{Q} g\rangle+\sum_{m=1}^{\lfloor N/2\rfloor}\left(\frac{N-2m}{N}\right)\langle g,\mathcal{Q}^{2m}g\rangle\nonumber\\ &\;\;\;\;\;\;\;\qquad+\sum_{m=1}^{\lfloor (N-1)/2\rfloor}\left(\frac{N-(2m+1)}{N}\right)\langle g,\mathcal{Q}^{2m+1}g\rangle\nonumber\\ \;&\geq\;\left(\frac{N-1}{N}\right)\langle g,\mathcal{Q} g\rangle+\left(\frac{\lfloor\frac{N-1}{2}\rfloor}{N}\right)\left\lVert g\right\rVert^2. \end{align}
\begin{align} \sum_{k=1}^N\left(\frac{N-k}{N}\right)\langle g,\mathcal{Q}^kg\rangle\;&=\;\left(\frac{N-1}{N}\right)\langle g,\mathcal{Q} g\rangle+\sum_{m=1}^{\lfloor N/2\rfloor}\left(\frac{N-2m}{N}\right)\langle g,\mathcal{Q}^{2m}g\rangle\nonumber\\ &\;\;\;\;\;\;\;\qquad+\sum_{m=1}^{\lfloor (N-1)/2\rfloor}\left(\frac{N-(2m+1)}{N}\right)\langle g,\mathcal{Q}^{2m+1}g\rangle\nonumber\\ \;&\geq\;\left(\frac{N-1}{N}\right)\langle g,\mathcal{Q} g\rangle+\left(\frac{\lfloor\frac{N-1}{2}\rfloor}{N}\right)\left\lVert g\right\rVert^2. \end{align}
By (3) and (10), as
![]() $f_0\perp g$
and
$f_0\perp g$
and
![]() $\mathcal{Q} f_0=f_0$
(by the definition of
$\mathcal{Q} f_0=f_0$
(by the definition of
![]() $\mathbf{E}_{\mathcal{Q}}(1)$
), this implies
$\mathbf{E}_{\mathcal{Q}}(1)$
), this implies
 \begin{align*} v(\,f,Q)\;&=\;\lim_{N\to\infty}\left[\left\lVert f\right\rVert^2+2\sum_{k=1}^N\left(\frac{N-k}{N}\right)\left(\left\lVert f_0\right\rVert^2+\langle g,\mathcal{Q}^k g\rangle\right)\right]\\ \;&\geq\;\left\lVert f\right\rVert^2+2\left\lVert f_0\right\rVert^2\lim_{N\to\infty}\left[\sum_{k=1}^N\left(\frac{N-k}{N}\right)\right]+2\langle g,\mathcal{Q} g\rangle+\left\lVert g\right\rVert^2\;=\;\infty \end{align*}
\begin{align*} v(\,f,Q)\;&=\;\lim_{N\to\infty}\left[\left\lVert f\right\rVert^2+2\sum_{k=1}^N\left(\frac{N-k}{N}\right)\left(\left\lVert f_0\right\rVert^2+\langle g,\mathcal{Q}^k g\rangle\right)\right]\\ \;&\geq\;\left\lVert f\right\rVert^2+2\left\lVert f_0\right\rVert^2\lim_{N\to\infty}\left[\sum_{k=1}^N\left(\frac{N-k}{N}\right)\right]+2\langle g,\mathcal{Q} g\rangle+\left\lVert g\right\rVert^2\;=\;\infty \end{align*}
as
![]() $\lim_{N\to\infty}\left[\sum_{k=1}^N\left(\frac{N-k}{N}\right)\right]=\infty$
. So trivially,
$\lim_{N\to\infty}\left[\sum_{k=1}^N\left(\frac{N-k}{N}\right)\right]=\infty$
. So trivially,
![]() $v(\,f,P)\leq\infty=v(\,f,Q)$
. Say
$v(\,f,P)\leq\infty=v(\,f,Q)$
. Say
![]() $f\in L^2_0(\pi)$
with
$f\in L^2_0(\pi)$
with
![]() $\mathcal{E}_{f,\mathcal{Q}}(\{1\})=0$
. If
$\mathcal{E}_{f,\mathcal{Q}}(\{1\})=0$
. If
![]() $\mathcal{E}_{f,\mathcal{P}}(\{1\})\neq0$
, again by fact 3 we have
$\mathcal{E}_{f,\mathcal{P}}(\{1\})\neq0$
, again by fact 3 we have
![]() $f=f_0+g$
for some
$f=f_0+g$
for some
![]() $f_0\in\mathbf{E}_{\mathcal{P}}(1)$
and
$f_0\in\mathbf{E}_{\mathcal{P}}(1)$
and
![]() $g\in\mathbf{E}_{\mathcal{P}}(1)^{\perp}$
. However by fact 2, we find that
$g\in\mathbf{E}_{\mathcal{P}}(1)^{\perp}$
. However by fact 2, we find that
![]() $f_0\in\mathbf{E}_{\mathcal{Q}}(1)$
as well, and just as in the above,
$f_0\in\mathbf{E}_{\mathcal{Q}}(1)$
as well, and just as in the above,
![]() $v(\,f,Q)=\infty$
, so trivially
$v(\,f,Q)=\infty$
, so trivially
![]() $v(\,f,P)\leq\infty=v(\,f,Q)$
. Finally, if
$v(\,f,P)\leq\infty=v(\,f,Q)$
. Finally, if
![]() $\mathcal{E}_{f,\mathcal{P}}(\{1\})=0$
then by fact 1, the above proof for the
$\mathcal{E}_{f,\mathcal{P}}(\{1\})=0$
then by fact 1, the above proof for the
![]() $\varphi$
-irreducible case follows almost exactly to show that
$\varphi$
-irreducible case follows almost exactly to show that
![]() $v(\,f,P)\leq v(\,f,Q)$
.
$v(\,f,P)\leq v(\,f,Q)$
.
Remark 4.1. For the other direction of Theorem 4.1, it is hard to make use of any arguments using Lemma 4.1. If P efficiency-dominates Q, we have that each individual
![]() $f\in L^2_0(\pi)$
satisfies
$f\in L^2_0(\pi)$
satisfies
![]() $\lim_{\eta\to1^-}\langle f,T_{\mathcal{P},\eta}^{-1}f\rangle\leq \lim_{\eta\to1^-}\langle f,T_{\mathcal{Q},\eta}^{-1}f\rangle$
. As we cannot apply Lemma 4.1 to the limits above, it seems the most we can do is fix an
$\lim_{\eta\to1^-}\langle f,T_{\mathcal{P},\eta}^{-1}f\rangle\leq \lim_{\eta\to1^-}\langle f,T_{\mathcal{Q},\eta}^{-1}f\rangle$
. As we cannot apply Lemma 4.1 to the limits above, it seems the most we can do is fix an
![]() $\epsilon>0$
, and by the above limit for every
$\epsilon>0$
, and by the above limit for every
![]() $f\in L^2_0(\pi)$
there exists
$f\in L^2_0(\pi)$
there exists
![]() $\eta_f\in[0,1)$
such that for every
$\eta_f\in[0,1)$
such that for every
![]() $\eta_f\leq\eta<1$
,
$\eta_f\leq\eta<1$
,
![]() $\langle f,T_{\mathcal{P},\eta}^{-1}f\rangle\leq \langle f,T_{\mathcal{Q},\eta}^{-1}f\rangle+\epsilon\left\lVert f\right\rVert^2=\left\langle \,f,\left(T^{-1}_{\mathcal{Q},\eta_f}+\epsilon\mathcal{I}\right) f\right\rangle$
. However, this results in a possibly different
$\langle f,T_{\mathcal{P},\eta}^{-1}f\rangle\leq \langle f,T_{\mathcal{Q},\eta}^{-1}f\rangle+\epsilon\left\lVert f\right\rVert^2=\left\langle \,f,\left(T^{-1}_{\mathcal{Q},\eta_f}+\epsilon\mathcal{I}\right) f\right\rangle$
. However, this results in a possibly different
![]() $\eta_f$
for every
$\eta_f$
for every
![]() $f\in L^2_0(\pi)$
, and it is not obvious that
$f\in L^2_0(\pi)$
, and it is not obvious that
![]() $\sup\{\eta_f\,:\,f\in L^2_0(\pi)\}<1$
, leaving us with no single
$\sup\{\eta_f\,:\,f\in L^2_0(\pi)\}<1$
, leaving us with no single
![]() $\eta\in[0,1)$
such that the above inequality holds for every
$\eta\in[0,1)$
such that the above inequality holds for every
![]() $f\in L^2_0(\pi)$
to allow us to apply Lemma 4.1.
$f\in L^2_0(\pi)$
to allow us to apply Lemma 4.1.
Because of the difficulties in applying Lemma 4.1 in the ‘only if’ direction of Theorem 4.1, we use the following lemma, which appears as Corollary 3.1 in [Reference Mira and Geyer18].
Lemma 4.2. Let T and N be injective self-adjoint positive bounded linear operators on the Hilbert space
![]() $\mathbf{H}$
(although
$\mathbf{H}$
(although
![]() $T^{-1/2}$
and
$T^{-1/2}$
and
![]() $N^{-1/2}$
may be unbounded). If
$N^{-1/2}$
may be unbounded). If
![]() $\textrm{domain}(T^{-1/2})\subseteq\textrm{domain}(N^{-1/2})$
and for every
$\textrm{domain}(T^{-1/2})\subseteq\textrm{domain}(N^{-1/2})$
and for every
![]() $f\in\textrm{domain}(T^{-1/2})$
we have
$f\in\textrm{domain}(T^{-1/2})$
we have
![]() $\left\lVert N^{-1/2}f\right\rVert\leq\left\lVert T^{-1/2}f\right\rVert$
, then
$\left\lVert N^{-1/2}f\right\rVert\leq\left\lVert T^{-1/2}f\right\rVert$
, then
![]() $\langle f,Tf\rangle\leq\langle f,Nf\rangle$
for every
$\langle f,Tf\rangle\leq\langle f,Nf\rangle$
for every
![]() $f\in\mathbf{H}$
.
$f\in\mathbf{H}$
.
See Section 7.2 for the proof of Lemma 4.2.
We must also use the fact that the space of functions with finite asymptotic variance is the domain of
![]() $\left(\mathcal{I}-\mathcal{P}\right)^{-1/2}$
. This was first stated in [Reference Kipnis and Varadhan15], by means of a test function argument. We take a different approach and provide a proof using the ideas of the spectral theorem. In particular, it uses some ideas from the proof of Theorem X.4.7 in [Reference Conway6].
$\left(\mathcal{I}-\mathcal{P}\right)^{-1/2}$
. This was first stated in [Reference Kipnis and Varadhan15], by means of a test function argument. We take a different approach and provide a proof using the ideas of the spectral theorem. In particular, it uses some ideas from the proof of Theorem X.4.7 in [Reference Conway6].
Lemma 4.3. If P is a
![]() $\varphi$
-irreducible Markov kernel reversible with respect to
$\varphi$
-irreducible Markov kernel reversible with respect to
![]() $\pi$
, then
$\pi$
, then
Proof. Let
![]() $\phi\,:\,[\!-1,1]\to\mathbf{R}$
such that
$\phi\,:\,[\!-1,1]\to\mathbf{R}$
such that
![]() $\phi(\lambda)=(1-\lambda)^{-1/2}$
for every
$\phi(\lambda)=(1-\lambda)^{-1/2}$
for every
![]() $\lambda\in[\!-1,1)$
and
$\lambda\in[\!-1,1)$
and
![]() $\phi(1)=0$
.
$\phi(1)=0$
.
Even though
![]() $\phi$
is unbounded, it still follows from spectral theory that
$\phi$
is unbounded, it still follows from spectral theory that
![]() $\int\phi \mathrm{d}\mathcal{E}_{\mathcal{P}}\:=\:\int\left(1-\lambda\right)^{-1/2}\mathcal{E}_{\mathcal{P}}(\mathrm{d}\lambda) \:=\:\left(\mathcal{I}-\mathcal{P}\right)^{-1/2}$
, the inverse operator of
$\int\phi \mathrm{d}\mathcal{E}_{\mathcal{P}}\:=\:\int\left(1-\lambda\right)^{-1/2}\mathcal{E}_{\mathcal{P}}(\mathrm{d}\lambda) \:=\:\left(\mathcal{I}-\mathcal{P}\right)^{-1/2}$
, the inverse operator of
![]() $\left(\mathcal{I}-\mathcal{P}\right)^{1/2}$
, including equality of domains (for a formal argument, see Theorem XII.2.9 in [Reference Dunford and Schwartz8]). Thus, our problem reduces to showing that
$\left(\mathcal{I}-\mathcal{P}\right)^{1/2}$
, including equality of domains (for a formal argument, see Theorem XII.2.9 in [Reference Dunford and Schwartz8]). Thus, our problem reduces to showing that
![]() $\left\{f\in L^2_0(\pi):v(\,f,P)<\infty\right\}=\textrm{domain}\left(\int\phi \mathrm{d}\mathcal{E}_{\mathcal{P}}\right)$
.
$\left\{f\in L^2_0(\pi):v(\,f,P)<\infty\right\}=\textrm{domain}\left(\int\phi \mathrm{d}\mathcal{E}_{\mathcal{P}}\right)$
.
Now notice that for every
![]() $f\in L^2_0(\pi)$
, as
$f\in L^2_0(\pi)$
, as
![]() $\mathcal{E}_{f,\mathcal{P}}(\{1\})=0$
by Lemma 3.1,
$\mathcal{E}_{f,\mathcal{P}}(\{1\})=0$
by Lemma 3.1,
Thus, by Theorem 3.1, for every
![]() $f\in L^2_0(\pi)$
,
$f\in L^2_0(\pi)$
,
![]() $v(\,f,P)=\int_{[\!-1,1)}\left(\frac{1+\lambda}{1-\lambda}\right)\mathcal{E}_{f,\mathcal{P}}(\mathrm{d}\lambda)$
, so
$v(\,f,P)=\int_{[\!-1,1)}\left(\frac{1+\lambda}{1-\lambda}\right)\mathcal{E}_{f,\mathcal{P}}(\mathrm{d}\lambda)$
, so
Thus, we would like to show that
![]() $\int\left|\phi\right|^2\mathrm{d}\mathcal{E}_{f,\mathcal{P}}$
is finite if and only if
$\int\left|\phi\right|^2\mathrm{d}\mathcal{E}_{f,\mathcal{P}}$
is finite if and only if
![]() $f\in\textrm{domain}\left(\int\phi \mathrm{d}\mathcal{E}_{\mathcal{P}}\right)$
.
$f\in\textrm{domain}\left(\int\phi \mathrm{d}\mathcal{E}_{\mathcal{P}}\right)$
.
For every
![]() $n\in\mathbf{N}$
, let
$n\in\mathbf{N}$
, let
![]() $\phi_n:=\mathbf{1}_{\left(\left|\phi\right| < n\right)}\,\phi$
and
$\phi_n:=\mathbf{1}_{\left(\left|\phi\right| < n\right)}\,\phi$
and
![]() $\Delta_n:=\phi^{-1}((\!-n,n))=\phi^{-1}_n(\mathbf{R})$
. Then notice
$\Delta_n:=\phi^{-1}((\!-n,n))=\phi^{-1}_n(\mathbf{R})$
. Then notice
![]() $\bigcup_{k=1}^{\infty}\Delta_n=\mathbf{R}$
and
$\bigcup_{k=1}^{\infty}\Delta_n=\mathbf{R}$
and
![]() $\Delta_n$
is a Borel set for every n as
$\Delta_n$
is a Borel set for every n as
![]() $\phi$
is Borel measurable.
$\phi$
is Borel measurable.
As
![]() $\phi$
is positive, notice hat
$\phi$
is positive, notice hat
![]() $\phi_n\leq\phi_{n+1}$
for every n. Thus, as
$\phi_n\leq\phi_{n+1}$
for every n. Thus, as
![]() $\phi_n\to\phi$
pointwise for every
$\phi_n\to\phi$
pointwise for every
![]() $\lambda\in\sigma(\mathcal{P})$
, by the monotone convergence theorem,
$\lambda\in\sigma(\mathcal{P})$
, by the monotone convergence theorem,
As
![]() $\phi_n$
is bounded for every n, by the definition of
$\phi_n$
is bounded for every n, by the definition of
![]() $\phi_n$
we have
$\phi_n$
we have
 \begin{align*} \int\left|\phi_n\right|^2\mathrm{d}\mathcal{E}_{f,\mathcal{P}} &\:=\:\left\lVert\left(\int\phi_n\mathrm{d}\mathcal{E}_{\mathcal{P}}\right)f\right\rVert^2\\ &\:=\:\left\lVert\left(\int\phi \mathrm{d}\mathcal{E}_{\mathcal{P}}\right)\mathcal{E}_{\mathcal{P}}\left( \bigcup_{k=1}^n\Delta_k\right)f\right\rVert^2\\ &\:=\:\left\lVert\mathcal{E}_{\mathcal{P}}\left(\bigcup_{k=1}^n\Delta_k\right) \left(\int\phi \mathrm{d}\mathcal{E}_{\mathcal{P}}\right)f\right\rVert^2. \end{align*}
\begin{align*} \int\left|\phi_n\right|^2\mathrm{d}\mathcal{E}_{f,\mathcal{P}} &\:=\:\left\lVert\left(\int\phi_n\mathrm{d}\mathcal{E}_{\mathcal{P}}\right)f\right\rVert^2\\ &\:=\:\left\lVert\left(\int\phi \mathrm{d}\mathcal{E}_{\mathcal{P}}\right)\mathcal{E}_{\mathcal{P}}\left( \bigcup_{k=1}^n\Delta_k\right)f\right\rVert^2\\ &\:=\:\left\lVert\mathcal{E}_{\mathcal{P}}\left(\bigcup_{k=1}^n\Delta_k\right) \left(\int\phi \mathrm{d}\mathcal{E}_{\mathcal{P}}\right)f\right\rVert^2. \end{align*}
Thus, as
![]() $\mathcal{E}_{\mathcal{P}}(\bigcup_{k=1}^n\Delta_k)\to\mathcal{E}_{\mathcal{P}}(\mathbf{R})=\mathcal{I}$
as
$\mathcal{E}_{\mathcal{P}}(\bigcup_{k=1}^n\Delta_k)\to\mathcal{E}_{\mathcal{P}}(\mathbf{R})=\mathcal{I}$
as
![]() $n\to\infty$
in the strong operator topology (i.e.
$n\to\infty$
in the strong operator topology (i.e.
![]() $\left\lVert\mathcal{E}_{\mathcal{P}}(\bigcup_{k=1}^n\Delta_k)f-f\right\rVert\to0$
for every
$\left\lVert\mathcal{E}_{\mathcal{P}}(\bigcup_{k=1}^n\Delta_k)f-f\right\rVert\to0$
for every
![]() $f\in L^2_0(\pi)$
), we have
$f\in L^2_0(\pi)$
), we have
 \begin{equation} \int\left|\phi_n\right|^2\mathrm{d}\mathcal{E}_{f,\mathcal{P}} \:=\:\left\lVert\mathcal{E}_{\mathcal{P}}\left(\bigcup_{k=1}^n\Delta_k\right)\left(\int\phi \mathrm{d}\mathcal{E}_{\mathcal{P}}\right)f\right\rVert^2 \:\to\:\left\lVert\left(\int\phi \mathrm{d}\mathcal{E}_{\mathcal{P}}\right)f\right\rVert^2. \end{equation}
\begin{equation} \int\left|\phi_n\right|^2\mathrm{d}\mathcal{E}_{f,\mathcal{P}} \:=\:\left\lVert\mathcal{E}_{\mathcal{P}}\left(\bigcup_{k=1}^n\Delta_k\right)\left(\int\phi \mathrm{d}\mathcal{E}_{\mathcal{P}}\right)f\right\rVert^2 \:\to\:\left\lVert\left(\int\phi \mathrm{d}\mathcal{E}_{\mathcal{P}}\right)f\right\rVert^2. \end{equation}
Thus, by (11) and (12) we have
Thus, as
![]() $\left\lVert\left(\int\phi \mathrm{d}\mathcal{E}_{\mathcal{P}}\right)f\right\rVert^2<\infty$
if and only if
$\left\lVert\left(\int\phi \mathrm{d}\mathcal{E}_{\mathcal{P}}\right)f\right\rVert^2<\infty$
if and only if
![]() $f\in\textrm{domain}\left(\int\phi \mathrm{d}\mathcal{E}_{\mathcal{P}}\right)$
, this completes the proof.
$f\in\textrm{domain}\left(\int\phi \mathrm{d}\mathcal{E}_{\mathcal{P}}\right)$
, this completes the proof.
Remark 4.2. Kipnis and Varadhan [Reference Kipnis and Varadhan15] state that
![]() $\{f\in L^2_0(\pi)\,:\,v(\,f,P)<\infty\}=\textrm{range}\left[\left(\mathcal{I}-\mathcal{P}\right)^{1/2}\right]$
. As
$\{f\in L^2_0(\pi)\,:\,v(\,f,P)<\infty\}=\textrm{range}\left[\left(\mathcal{I}-\mathcal{P}\right)^{1/2}\right]$
. As
![]() $\textrm{range}\left[\left(\mathcal{I}-\mathcal{P}\right)^{1/2}\right]= \textrm{domain}\left[\left(\mathcal{I}-\mathcal{P}\right)^{-1/2}\right]$
, these are equivalent.
$\textrm{range}\left[\left(\mathcal{I}-\mathcal{P}\right)^{1/2}\right]= \textrm{domain}\left[\left(\mathcal{I}-\mathcal{P}\right)^{-1/2}\right]$
, these are equivalent.
Now we are ready to prove the ‘only if’ direction of Theorem 4.1, as outlined in [Reference Mira and Geyer18]. Recall the ‘only if’ direction of Theorem 4.1; if P and Q are Markov kernels reversible with respect to
![]() $\pi$
, such that P efficiency-dominates Q, then
$\pi$
, such that P efficiency-dominates Q, then
![]() $\langle f,\mathcal{P} f\rangle\leq\langle f,\mathcal{Q} f\rangle$
for every
$\langle f,\mathcal{P} f\rangle\leq\langle f,\mathcal{Q} f\rangle$
for every
![]() $f\in L^2_0(\pi)$
.
$f\in L^2_0(\pi)$
.
Proof of ‘only if’ direction of Theorem 4.1. As P efficiency-dominates Q, if
![]() $f\in L^2_0(\pi)$
such that
$f\in L^2_0(\pi)$
such that
![]() $v(\,f,Q)<\infty$
then
$v(\,f,Q)<\infty$
then
![]() $v(\,f,P)\leq v(\,f,Q)<\infty$
. Thus,
$v(\,f,P)\leq v(\,f,Q)<\infty$
. Thus,
![]() $\{f\in L^2_0(\pi)\,:\,v(\,f,Q)<\infty\}\subseteq\{f\in L^2_0(\pi)\,:\,v(\,f,P)<\infty\}$
. So by Lemma 4.3, we have
$\{f\in L^2_0(\pi)\,:\,v(\,f,Q)<\infty\}\subseteq\{f\in L^2_0(\pi)\,:\,v(\,f,P)<\infty\}$
. So by Lemma 4.3, we have
Notice that for every
![]() $\lambda\neq1$
,
$\lambda\neq1$
,
![]() $\frac{1}{1-\lambda}=\frac{1}{2}\left(1+\frac{1+\lambda}{1-\lambda}\right)$
. Thus, by Theorem 3.1, for every
$\frac{1}{1-\lambda}=\frac{1}{2}\left(1+\frac{1+\lambda}{1-\lambda}\right)$
. Thus, by Theorem 3.1, for every
![]() $f\in \textrm{domain}\left[\left(\mathcal{I}-\mathcal{P}\right)^{-1/2}\right]$
(as if
$f\in \textrm{domain}\left[\left(\mathcal{I}-\mathcal{P}\right)^{-1/2}\right]$
(as if
![]() $f\in L^2_0(\pi)$
with
$f\in L^2_0(\pi)$
with
![]() $v(\,f,P)<\infty$
then necessarily
$v(\,f,P)<\infty$
then necessarily
![]() $\mathcal{E}_{f,\mathcal{P}}(\{1\})=0$
),
$\mathcal{E}_{f,\mathcal{P}}(\{1\})=0$
),
and similarly for Q. As P efficiency-dominates Q, for every
![]() $f\in\\\textrm{domain}\left[\left(\mathcal{I}-\mathcal{Q}\right)^{-1/2}\right]$
,
$f\in\\\textrm{domain}\left[\left(\mathcal{I}-\mathcal{Q}\right)^{-1/2}\right]$
,
Furthermore, by (13) in the proof of Lemma 4.3, (recall that
![]() $\phi(\lambda)=(1-\lambda)^{-1/2}$
in the proof of Lemma 4.3), for every
$\phi(\lambda)=(1-\lambda)^{-1/2}$
in the proof of Lemma 4.3), for every
![]() $f\in\textrm{domain}\left[\left(\mathcal{I}-\mathcal{P}\right)^{-1/2}\right]$
,
$f\in\textrm{domain}\left[\left(\mathcal{I}-\mathcal{P}\right)^{-1/2}\right]$
,
and similarly
![]() $\int_{[\!-1,1)}\left(\frac{1}{1-\lambda}\right)\mathcal{E}_{f,\mathcal{Q}}(\mathrm{d}\lambda)= \left\lVert\left(\mathcal{I}-\mathcal{Q}\right)^{-1/2}f\right\rVert^2$
. Thus, by (14) and (15), for every
$\int_{[\!-1,1)}\left(\frac{1}{1-\lambda}\right)\mathcal{E}_{f,\mathcal{Q}}(\mathrm{d}\lambda)= \left\lVert\left(\mathcal{I}-\mathcal{Q}\right)^{-1/2}f\right\rVert^2$
. Thus, by (14) and (15), for every
![]() $f\in\textrm{domain}\left[\left(\mathcal{I}-\mathcal{Q}\right)^{-1/2}\right]$
,
$f\in\textrm{domain}\left[\left(\mathcal{I}-\mathcal{Q}\right)^{-1/2}\right]$
,
So by Lemma 4.2, with
![]() $T=\left(\mathcal{I}-\mathcal{Q}\right)$
and
$T=\left(\mathcal{I}-\mathcal{Q}\right)$
and
![]() $N=\left(\mathcal{I}-\mathcal{P}\right)$
, for every
$N=\left(\mathcal{I}-\mathcal{P}\right)$
, for every
![]() $f\in L^2_0(\pi)$
,
$f\in L^2_0(\pi)$
,
![]() $\langle f,\left(\mathcal{I}-\mathcal{Q}\right)f\rangle\leq\langle f,\left(\mathcal{I}-\mathcal{P}\right)f\rangle$
, and thus
$\langle f,\left(\mathcal{I}-\mathcal{Q}\right)f\rangle\leq\langle f,\left(\mathcal{I}-\mathcal{P}\right)f\rangle$
, and thus
The condition (8) is clearly equivalent to
![]() $\langle f,\left(\mathcal{Q}-\mathcal{P}\right)f\rangle\geq0$
for every
$\langle f,\left(\mathcal{Q}-\mathcal{P}\right)f\rangle\geq0$
for every
![]() $f\in L^2_0(\pi)$
, i.e. equivalent to
$f\in L^2_0(\pi)$
, i.e. equivalent to
![]() $\mathcal{Q}-\mathcal{P}$
being a positive operator. We can relate this back to the spectrum of the operator
$\mathcal{Q}-\mathcal{P}$
being a positive operator. We can relate this back to the spectrum of the operator
![]() $\mathcal{Q}-\mathcal{P}$
with the following lemma.
$\mathcal{Q}-\mathcal{P}$
with the following lemma.
Lemma 4.4. If T is a bounded self-adjoint linear operator on a Hilbert space
![]() $\mathbf{H}$
, then T is positive if and only if
$\mathbf{H}$
, then T is positive if and only if
![]() $\sigma(T)\subseteq[0,\infty)$
.
$\sigma(T)\subseteq[0,\infty)$
.
Proof. For the forward direction, if
![]() $\lambda<0$
then for every
$\lambda<0$
then for every
![]() $f\in\mathbf{H}$
such that
$f\in\mathbf{H}$
such that
![]() $f\neq0$
, by the Cauchy–Schwarz inequality,
$f\neq0$
, by the Cauchy–Schwarz inequality,
 \begin{align*} \left\lVert(T-\lambda)f\right\rVert\left\lVert f\right\rVert &\geq|\langle(T-\lambda)f,f\rangle|\\ &=|\langle Tf,f\rangle-\lambda\left\lVert f\right\rVert^2|\\ &\geq\langle Tf,f\rangle+|\lambda|\left\lVert f\right\rVert^2 &(\text{as $\lambda<0$ and by assumption})\\ &\geq|\lambda|\left\lVert f\right\rVert^2 &(\text{by assumption}). \end{align*}
\begin{align*} \left\lVert(T-\lambda)f\right\rVert\left\lVert f\right\rVert &\geq|\langle(T-\lambda)f,f\rangle|\\ &=|\langle Tf,f\rangle-\lambda\left\lVert f\right\rVert^2|\\ &\geq\langle Tf,f\rangle+|\lambda|\left\lVert f\right\rVert^2 &(\text{as $\lambda<0$ and by assumption})\\ &\geq|\lambda|\left\lVert f\right\rVert^2 &(\text{by assumption}). \end{align*}
Thus, as
![]() $f\neq0$
and
$f\neq0$
and
![]() $\lambda\neq0$
,
$\lambda\neq0$
,
Thus, as
![]() $T-\lambda$
is normal (as it is self-adjoint),
$T-\lambda$
is normal (as it is self-adjoint),
![]() $T-\lambda$
is invertible (by Lemma 7.2), and
$T-\lambda$
is invertible (by Lemma 7.2), and
![]() $\lambda\not\in\sigma(T)$
by definition.
$\lambda\not\in\sigma(T)$
by definition.
For the converse, if
![]() $\sigma(T)\subseteq[0,\infty)$
then as
$\sigma(T)\subseteq[0,\infty)$
then as
![]() $\mathcal{E}_{f,T}$
is a positive measure for every
$\mathcal{E}_{f,T}$
is a positive measure for every
![]() $f\in\mathbf{H}$
(as
$f\in\mathbf{H}$
(as
![]() $\mathcal{E}_{T}(A)$
is a self-adjoint projection for every Borel set A),
$\mathcal{E}_{T}(A)$
is a self-adjoint projection for every Borel set A),
This gives us the following theorem.
Theorem 4.2. If P and Q are Markov kernels reversible with respect to
![]() $\pi$
, then P efficiency-dominates Q if and only if
$\pi$
, then P efficiency-dominates Q if and only if
![]() $\sigma(\mathcal{Q}-\mathcal{P})\subseteq[0,\infty)$
, i.e.
$\sigma(\mathcal{Q}-\mathcal{P})\subseteq[0,\infty)$
, i.e.
![]() $\mathcal{Q}-\mathcal{P}$
is a positive operator.
$\mathcal{Q}-\mathcal{P}$
is a positive operator.
Proof. By Theorem 4.1, P efficiency-dominates Q if and only if
![]() $\mathcal{P}$
and
$\mathcal{P}$
and
![]() $\mathcal{Q}$
satisfy (8). As
$\mathcal{Q}$
satisfy (8). As
![]() $\mathcal{P}$
and
$\mathcal{P}$
and
![]() $\mathcal{Q}$
are both bounded linear operators, this is equivalent to
$\mathcal{Q}$
are both bounded linear operators, this is equivalent to
or in other words is equivalent to
![]() $\mathcal{Q}-\mathcal{P}$
being a positive operator.
$\mathcal{Q}-\mathcal{P}$
being a positive operator.
Thus, as
![]() $\mathcal{Q}-\mathcal{P}$
is a bounded self-adjoint linear operator on
$\mathcal{Q}-\mathcal{P}$
is a bounded self-adjoint linear operator on
![]() $L^2_0(\pi)$
, by Lemma 4.4,
$L^2_0(\pi)$
, by Lemma 4.4,
![]() $\mathcal{Q}-\mathcal{P}$
is a positive operator if and only if
$\mathcal{Q}-\mathcal{P}$
is a positive operator if and only if
![]() $\sigma(\mathcal{Q}-\mathcal{P})\subseteq[0,\infty)$
.
$\sigma(\mathcal{Q}-\mathcal{P})\subseteq[0,\infty)$
.
We now provide a simple, easy-to-check sufficient condition for efficiency dominance. The following result is a generalization of Theorem 14 in [Reference Neal and Rosenthal20], but with a notable difference. As discussed in Section 2.2, when we are dealing with general Hilbert spaces, as is the case for general state space algorithms, we need to consider the whole spectrum of the kernels, not only the eigenvalues, as is the case in [Reference Neal and Rosenthal20].
Proposition 4.1. If P and Q are Markov kernels reversible with respect to
![]() $\pi$
such that
$\pi$
such that
![]() $\sup\sigma(\mathcal{P})\leq\inf\sigma(\mathcal{Q})$
, then P efficiency-dominates Q.
$\sup\sigma(\mathcal{P})\leq\inf\sigma(\mathcal{Q})$
, then P efficiency-dominates Q.
Proof. Firstly, notice that for every
![]() $f\in L^2_0(\pi)$
,
$f\in L^2_0(\pi)$
,
and similarly
![]() $\langle f,\mathcal{Q} f\rangle\geq\inf\sigma(\mathcal{Q})\cdot\left\lVert f\right\rVert^2$
. Thus, for every
$\langle f,\mathcal{Q} f\rangle\geq\inf\sigma(\mathcal{Q})\cdot\left\lVert f\right\rVert^2$
. Thus, for every
![]() $f\in L^2_0(\pi)$
,
$f\in L^2_0(\pi)$
,
and thus by Theorem 4.1, P efficiency-dominates Q.
Example 4.2. Rudolf and Ullrich [Reference Rudolf and Ullrich25] proved positivity (i.e. that
![]() $\sigma(\mathcal{P})\subseteq[0,\infty)$
) for many general state space MCMC algorithms. In particular, they used the fact that conjugation of a positive operator by a bounded operator is again a positive operator, i.e. they showed that the corresponding Markov operator
$\sigma(\mathcal{P})\subseteq[0,\infty)$
) for many general state space MCMC algorithms. In particular, they used the fact that conjugation of a positive operator by a bounded operator is again a positive operator, i.e. they showed that the corresponding Markov operator
![]() $\mathcal{P}$
of each algorithm is of the form
$\mathcal{P}$
of each algorithm is of the form
![]() $MTM^*$
, where
$MTM^*$
, where
![]() $M\,:\,\mathbf{H}\to L^2_0(\pi)$
is a bounded linear operator from some Hilbert space
$M\,:\,\mathbf{H}\to L^2_0(\pi)$
is a bounded linear operator from some Hilbert space
![]() $\mathbf{H}$
,
$\mathbf{H}$
,
![]() $M^*:L^2_0(\pi)\to\mathbf{H}$
is its adjoint operator (see Section 2.2), and
$M^*:L^2_0(\pi)\to\mathbf{H}$
is its adjoint operator (see Section 2.2), and
![]() $T:\mathbf{H}\to\mathbf{H}$
is a self-adjoint positive operator on
$T:\mathbf{H}\to\mathbf{H}$
is a self-adjoint positive operator on
![]() $\mathbf{H}$
.
$\mathbf{H}$
.
For context, let
![]() $n\geq1$
,
$n\geq1$
,
![]() $K\subseteq\mathbf{R}^n$
with nonempty interior, and
$K\subseteq\mathbf{R}^n$
with nonempty interior, and
![]() $f:K\to[0,\infty)$
be a possibly unnormalized probability density. Rudolf and Ullrich [Reference Rudolf and Ullrich25] proved positivity for the following algorithms.
$f:K\to[0,\infty)$
be a possibly unnormalized probability density. Rudolf and Ullrich [Reference Rudolf and Ullrich25] proved positivity for the following algorithms.
-
(i) Hit-and-run algorithm.
-
• Starting at
 $x_k\in K$
, choose a direction
$x_k\in K$
, choose a direction
 $\theta$
in the (
$\theta$
in the (
 $n-1$
)-dimensional unit sphere uniformly at random, and then sample
$n-1$
)-dimensional unit sphere uniformly at random, and then sample
 $x_{k+1}\in K$
from f restricted to the one-dimensional subset
$x_{k+1}\in K$
from f restricted to the one-dimensional subset
 $\{x+\delta\theta:\delta\in\mathbf{R}\text{ such that }x+\delta\theta\in K\}$
.
$\{x+\delta\theta:\delta\in\mathbf{R}\text{ such that }x+\delta\theta\in K\}$
.
-
-
(ii) Random scan Gibbs sampler algorithm.
-
• Starting at
 $x_k\in K$
, choose an axis
$x_k\in K$
, choose an axis
 $j\in\{1,\ldots,n\}$
uniformly at random, and then sample
$j\in\{1,\ldots,n\}$
uniformly at random, and then sample
 $x_{k+1}\in K$
from f restricted to the one-dimensional subset
$x_{k+1}\in K$
from f restricted to the one-dimensional subset
 $\{x+\delta e_j:\delta\in\mathbf{R}\text{ such that }x+\delta e_j\in K\}$
, where
$\{x+\delta e_j:\delta\in\mathbf{R}\text{ such that }x+\delta e_j\in K\}$
, where
 $e_j$
is the jth coordinate vector of
$e_j$
is the jth coordinate vector of
 $\mathbf{R}^n$
.
$\mathbf{R}^n$
.
-
-
(iii) Slice sampler algorithm.
-
• (Simple slice sampler) Starting at
 $x_k\in K$
, choose a level
$x_k\in K$
, choose a level
 $t\in(0,f(x_k)]$
uniformly at random, and then sample
$t\in(0,f(x_k)]$
uniformly at random, and then sample
 $x_{k+1}\in K$
uniformly at random from the set
$x_{k+1}\in K$
uniformly at random from the set
 $\{x\in K\,:\,f(x)\geq t\}\,=\!:\,f^{-1}([t,\infty))$
. (Rudolf and Ullrich [Reference Rudolf and Ullrich25] proved positivity for more general slice sampler algorithms, allowing for more general transitions once a level t is chosen, not only uniform transitions.)
$\{x\in K\,:\,f(x)\geq t\}\,=\!:\,f^{-1}([t,\infty))$
. (Rudolf and Ullrich [Reference Rudolf and Ullrich25] proved positivity for more general slice sampler algorithms, allowing for more general transitions once a level t is chosen, not only uniform transitions.)
-
-
(iv) Metropolis algorithm.
-
• Given any Markov kernel Q that is reversible with respect to the Lebesgue measure and positive, given
 $x_k\in K$
, generate a sample
$x_k\in K$
, generate a sample
 $y\in K$
from
$y\in K$
from
 $Q(x_k,\cdot)$
, and accept the proposal and set
$Q(x_k,\cdot)$
, and accept the proposal and set
 $x_{k+1}=y$
with probability
$x_{k+1}=y$
with probability
 $\alpha(x_k,y)=\min\{1,\frac{f(y)}{f(x)}\}$
and reject the proposal and set
$\alpha(x_k,y)=\min\{1,\frac{f(y)}{f(x)}\}$
and reject the proposal and set
 $x_{k+1}=x_k$
with probability
$x_{k+1}=x_k$
with probability
 $1-\alpha(x_k,y)$
.
$1-\alpha(x_k,y)$
.
-
Recall from Section 2.1 that
![]() $\Pi\equiv0$
, where
$\Pi\equiv0$
, where
![]() $\Pi$
is the Markov kernel corresponding to i.i.d. sampling from
$\Pi$
is the Markov kernel corresponding to i.i.d. sampling from
![]() $\pi$
. Thus, clearly
$\pi$
. Thus, clearly
![]() $\sigma(\Pi)=\{0\}$
, and as the algorithms above are positive, if we denote their Markov operator as
$\sigma(\Pi)=\{0\}$
, and as the algorithms above are positive, if we denote their Markov operator as
![]() $\mathcal{P}$
,
$\mathcal{P}$
,
![]() $\sigma(\mathcal{P})\subseteq[0,\infty)$
. So, in particular
$\sigma(\mathcal{P})\subseteq[0,\infty)$
. So, in particular
![]() $\inf\sigma(\mathcal{P})\geq0=\sup\sigma(\Pi)$
, and thus by Proposition 4.1, we find that i.i.d. sampling efficiency-dominates each of the algorithms above.
$\inf\sigma(\mathcal{P})\geq0=\sup\sigma(\Pi)$
, and thus by Proposition 4.1, we find that i.i.d. sampling efficiency-dominates each of the algorithms above.
As seen in [Reference Green and Han12], antithetic methods can lead to increased efficiency of MCMC methods. In this paper, we define antithetic Markov kernels as Markov kernels P such that
![]() $\sigma(\mathcal{P})\subseteq[\!-1,0]$
when restricted to
$\sigma(\mathcal{P})\subseteq[\!-1,0]$
when restricted to
![]() $L^2_0(\pi)$
. We will show here that antithetic reversible Markov kernels are more efficient than i.i.d. sampling from
$L^2_0(\pi)$
. We will show here that antithetic reversible Markov kernels are more efficient than i.i.d. sampling from
![]() $\pi$
directly, generalizing the result from [Reference Neal and Rosenthal20].
$\pi$
directly, generalizing the result from [Reference Neal and Rosenthal20].
Proposition 4.2. Let P be a Markov kernel reversible with respect to
![]() $\pi$
; then P is antithetic if and only if P efficiency-dominates
$\pi$
; then P is antithetic if and only if P efficiency-dominates
![]() $\Pi$
(the Markov kernel corresponding to i.i.d. sampling from
$\Pi$
(the Markov kernel corresponding to i.i.d. sampling from
![]() $\pi$
).
$\pi$
).
Proof. Recall from Section 2.1 that
![]() $\Pi\equiv0$
on
$\Pi\equiv0$
on
![]() $L^2_0(\pi)$
, and thus
$L^2_0(\pi)$
, and thus
![]() $\sigma(\Pi)=\{0\}$
.
$\sigma(\Pi)=\{0\}$
.
So say P is antithetic. Then
![]() $\sup\sigma(\mathcal{P})\leq0=\inf\sigma(\Pi)$
, and by Proposition 4.1, P efficiency-dominates
$\sup\sigma(\mathcal{P})\leq0=\inf\sigma(\Pi)$
, and by Proposition 4.1, P efficiency-dominates
![]() $\Pi$
.
$\Pi$
.
On the other hand, if P efficiency-dominates
![]() $\Pi$
then by Proposition 4.1,
$\Pi$
then by Proposition 4.1,
![]() $\sup\sigma(\mathcal{P})\leq\inf\sigma(\Pi)=0$
, and thus
$\sup\sigma(\mathcal{P})\leq\inf\sigma(\Pi)=0$
, and thus
![]() $\sigma(\mathcal{P})\subseteq(\!-\infty,0] \cap[\!-1,1]=[\!-1,0]$
, so P is antithetic.
$\sigma(\mathcal{P})\subseteq(\!-\infty,0] \cap[\!-1,1]=[\!-1,0]$
, so P is antithetic.
Example 4.3. Take
![]() $\left(\mathbf{X},\mathcal{F},\pi\right)\;=\;\left(\left[0,1\right],\mathcal{B},m\right)$
, where
$\left(\mathbf{X},\mathcal{F},\pi\right)\;=\;\left(\left[0,1\right],\mathcal{B},m\right)$
, where
![]() $\mathcal{B}$
is the Borel
$\mathcal{B}$
is the Borel
![]() $\sigma$
-field on [0,1] and m is the Lebesgue measure on [0,1], i.e.
$\sigma$
-field on [0,1] and m is the Lebesgue measure on [0,1], i.e.
![]() $(\mathbf{X},\mathcal{F},\pi)$
is the uniform probability space.
$(\mathbf{X},\mathcal{F},\pi)$
is the uniform probability space.
Denote the left and right halves of [0,1] by L and R, respectively, i.e.
![]() $L=[0,1/2]$
and
$L=[0,1/2]$
and
![]() $R=(1/2,1]$
. Then let P be the Markov kernel that jumps from the left half L to the right half R uniformly, and similarly from the right half R to the left half L uniformly, i.e.
$R=(1/2,1]$
. Then let P be the Markov kernel that jumps from the left half L to the right half R uniformly, and similarly from the right half R to the left half L uniformly, i.e.
![]() $P(x,\mathrm{d}y)\,=\,2\left(\mathbf{1}_{L}(x)m|_{R}(\mathrm{d}y)+\mathbf{1}_{R}(x)m|_{L}(\mathrm{d}y)\right)$
.
$P(x,\mathrm{d}y)\,=\,2\left(\mathbf{1}_{L}(x)m|_{R}(\mathrm{d}y)+\mathbf{1}_{R}(x)m|_{L}(\mathrm{d}y)\right)$
.
P is clearly reversible. Furthermore, notice that for every
![]() $f\in L^2_0(m)$
, as
$f\in L^2_0(m)$
, as
![]() $0=\mathbf{E}_m(f)=\int fdm=\int_{L}fdm +\int_{R}fdm$
,
$0=\mathbf{E}_m(f)=\int fdm=\int_{L}fdm +\int_{R}fdm$
,
![]() $-\int_{L}fdm=\int_{R}fdm$
, so
$-\int_{L}fdm=\int_{R}fdm$
, so
 \begin{align*} \langle f,\mathcal{P} f\rangle&=2\iint_{[0,1]}f(x)f(y)\left( \mathbf{1}_{L}(x)m|_{R}(\mathrm{d}y)+\mathbf{1}_{R}(x)m|_{L}(\mathrm{d}y)\right)m(\mathrm{d}x)\\ &=2\left(\int_{x\in L}\int_{y\in R}f(x)f(y)m(\mathrm{d}y)m(\mathrm{d}x)+\int_{x\in R}\int_{y\in L}f(x)f(y)m(\mathrm{d}y)m(\mathrm{d}x)\right)\\ &=2\left(\left(\int_{L}fdm\right)\left(\int_{R}fdm\right)+\left(\int_{R}fdm\right)\left(\int_{L}fdm\right)\right)\\ &=2\left(\left(\int_{L}fdm\right)\left(-\int_{L}fdm\right)+\left(-\int_{L}fdm\right)\left(\int_{L}fdm\right)\right)\\ &=-4\left(\int_{L}fdm\right)^2\;\leq\;0. \end{align*}
\begin{align*} \langle f,\mathcal{P} f\rangle&=2\iint_{[0,1]}f(x)f(y)\left( \mathbf{1}_{L}(x)m|_{R}(\mathrm{d}y)+\mathbf{1}_{R}(x)m|_{L}(\mathrm{d}y)\right)m(\mathrm{d}x)\\ &=2\left(\int_{x\in L}\int_{y\in R}f(x)f(y)m(\mathrm{d}y)m(\mathrm{d}x)+\int_{x\in R}\int_{y\in L}f(x)f(y)m(\mathrm{d}y)m(\mathrm{d}x)\right)\\ &=2\left(\left(\int_{L}fdm\right)\left(\int_{R}fdm\right)+\left(\int_{R}fdm\right)\left(\int_{L}fdm\right)\right)\\ &=2\left(\left(\int_{L}fdm\right)\left(-\int_{L}fdm\right)+\left(-\int_{L}fdm\right)\left(\int_{L}fdm\right)\right)\\ &=-4\left(\int_{L}fdm\right)^2\;\leq\;0. \end{align*}
Thus, we see that
![]() $-\mathcal{P}$
is a positive operator, and thus by Lemma 4.4,
$-\mathcal{P}$
is a positive operator, and thus by Lemma 4.4,
![]() $-\sigma(\mathcal{P})=\sigma(\!-\mathcal{P})\subseteq[0,\infty)$
, and thus
$-\sigma(\mathcal{P})=\sigma(\!-\mathcal{P})\subseteq[0,\infty)$
, and thus
![]() $\sigma(\mathcal{P})\subseteq(\!-\infty,0]$
. As
$\sigma(\mathcal{P})\subseteq(\!-\infty,0]$
. As
![]() $\mathcal{P}$
is an operator arising from a Markov kernel, we have
$\mathcal{P}$
is an operator arising from a Markov kernel, we have
![]() $\sigma(\mathcal{P})\subseteq[\!-1,0]$
, so P is antithetic.
$\sigma(\mathcal{P})\subseteq[\!-1,0]$
, so P is antithetic.
Thus, by Proposition 4.2, P efficiency-dominates i.i.d. sampling. So for every square-integrable Borel function f on the interval [0,1], we can achieve a lower variance in our Monte Carlo estimate using a Markov chain with P as its kernel than by i.i.d. sampling.
The above example illustrates that even in very simple scenarios we can improve our estimates using MCMC algorithms over i.i.d. sampling.
We now show that efficiency dominance is partial ordering on the set of reversible Markov kernels reversible with respect to
![]() $\pi$
, just as in [Reference Mira and Geyer18].
$\pi$
, just as in [Reference Mira and Geyer18].
Theorem 4.3. Efficiency dominance is a partial order on reversible Markov kernels, reversible with respect to
![]() $\pi$
(reversible with respect to the same probability measure).
$\pi$
(reversible with respect to the same probability measure).
Proof. Reflexivity and transitivity are trivial (as
![]() $v(\,f,P)\leq v(\,f,P)$
for every f and P, and if P efficiency-dominates Q and Q efficiency-dominates R then
$v(\,f,P)\leq v(\,f,P)$
for every f and P, and if P efficiency-dominates Q and Q efficiency-dominates R then
![]() $v(\,f,P)\leq v(\,f,Q)\leq v(\,f,R)$
for every
$v(\,f,P)\leq v(\,f,Q)\leq v(\,f,R)$
for every
![]() $f\in L^2_0(\pi)$
).
$f\in L^2_0(\pi)$
).
Suppose P and Q are reversible Markov kernels reversible with respect to
![]() $\pi$
such that P efficiency-dominates Q and Q efficiency-dominates P. Then by Theorem 4.1, for every
$\pi$
such that P efficiency-dominates Q and Q efficiency-dominates P. Then by Theorem 4.1, for every
![]() $f\in L^2_0(\pi)$
,
$f\in L^2_0(\pi)$
,
so
![]() $\langle f,\mathcal{P} f\rangle=\langle f,\mathcal{Q} f\rangle$
for every
$\langle f,\mathcal{P} f\rangle=\langle f,\mathcal{Q} f\rangle$
for every
![]() $f\in L^2_0(\pi)$
. Thus,
$f\in L^2_0(\pi)$
. Thus,
![]() $\langle f,(\mathcal{Q}-\mathcal{P})f\rangle=0$
for every
$\langle f,(\mathcal{Q}-\mathcal{P})f\rangle=0$
for every
![]() $f\in L^2_0(\pi)$
. So for every
$f\in L^2_0(\pi)$
. So for every
![]() $g,h\in L^2_0(\pi)$
, as
$g,h\in L^2_0(\pi)$
, as
![]() $\mathcal{Q}$
and
$\mathcal{Q}$
and
![]() $\mathcal{P}$
are self-adjoint,
$\mathcal{P}$
are self-adjoint,
 \begin{align*} 0 &=\langle g+h,(\mathcal{Q}-\mathcal{P})(g+h)\rangle\\ &=\langle g,(\mathcal{Q}-\mathcal{P})g\rangle+\langle h,(\mathcal{Q}-\mathcal{P})h\rangle +2\langle g,(\mathcal{Q}-\mathcal{P})h\rangle\\ &=2\langle g,(\mathcal{Q}-\mathcal{P})h\rangle. \end{align*}
\begin{align*} 0 &=\langle g+h,(\mathcal{Q}-\mathcal{P})(g+h)\rangle\\ &=\langle g,(\mathcal{Q}-\mathcal{P})g\rangle+\langle h,(\mathcal{Q}-\mathcal{P})h\rangle +2\langle g,(\mathcal{Q}-\mathcal{P})h\rangle\\ &=2\langle g,(\mathcal{Q}-\mathcal{P})h\rangle. \end{align*}
So for every
![]() $g,h\in L^2_0(\pi)$
,
$g,h\in L^2_0(\pi)$
,
![]() $\langle g,(\mathcal{Q}-\mathcal{P})h\rangle=0$
. Thus,
$\langle g,(\mathcal{Q}-\mathcal{P})h\rangle=0$
. Thus,
![]() $\mathcal{Q}-\mathcal{P}=0$
, so
$\mathcal{Q}-\mathcal{P}=0$
, so
![]() $\mathcal{P}=\mathcal{Q}$
, and thus
$\mathcal{P}=\mathcal{Q}$
, and thus
![]() $P=Q$
. So the relation is antisymmetric.
$P=Q$
. So the relation is antisymmetric.
5. Combining Chains
In this section, we generalize the results of Neal and Rosenthal [Reference Neal and Rosenthal20] on the efficiency dominance of combined chains from finite state spaces to general state spaces. We state the most general result first, a sufficient condition for the efficiency dominance of combined kernels, and then a simple corollary following from it.
Theorem 5.1. Let P and Q be Markov kernels such that
![]() $P = \sum\alpha_kP_k$
and
$P = \sum\alpha_kP_k$
and
![]() $Q = \sum\alpha_kQ_k$
, where
$Q = \sum\alpha_kQ_k$
, where
![]() $P_1,\ldots,P_l$
and
$P_1,\ldots,P_l$
and
![]() $Q_1,\ldots,Q_l$
are Markov kernels reversible with respect to
$Q_1,\ldots,Q_l$
are Markov kernels reversible with respect to
![]() $\pi$
, and
$\pi$
, and
![]() $\alpha_1,\ldots,\alpha_l$
are mixing probabilities (i.e.
$\alpha_1,\ldots,\alpha_l$
are mixing probabilities (i.e.
![]() $\alpha_k\geq0$
for every k, and
$\alpha_k\geq0$
for every k, and
![]() $\sum\alpha_k=1$
).
$\sum\alpha_k=1$
).
If
![]() $P_k$
efficiency-dominates
$P_k$
efficiency-dominates
![]() $Q_k$
for every k, then P efficiency-dominates Q.
$Q_k$
for every k, then P efficiency-dominates Q.
Proof. As
![]() $P_k$
efficiency-dominates
$P_k$
efficiency-dominates
![]() $Q_k$
for every k, by Theorem 4.2,
$Q_k$
for every k, by Theorem 4.2,
![]() $\mathcal{Q}_k-\mathcal{P}_k$
is a positive operator for every k. By the definition of a positive operator (Section 2.2), for every
$\mathcal{Q}_k-\mathcal{P}_k$
is a positive operator for every k. By the definition of a positive operator (Section 2.2), for every
![]() $k\in\{1,\ldots,l\}$
, we have
$k\in\{1,\ldots,l\}$
, we have
So for every
![]() $f\in L^2_0(\pi)$
,
$f\in L^2_0(\pi)$
,
Thus, as P and Q are also reversible (as each
![]() $P_k$
and
$P_k$
and
![]() $Q_k$
is reversible),
$Q_k$
is reversible),
![]() $\mathcal{P}$
and
$\mathcal{P}$
and
![]() $\mathcal{Q}$
satisfy (8), and thus by Theorem 4.1, P efficiency-dominates Q.
$\mathcal{Q}$
satisfy (8), and thus by Theorem 4.1, P efficiency-dominates Q.
The converse of Theorem 5.1 is not true, even in the case where
![]() $P_1,\ldots,P_l$
and
$P_1,\ldots,P_l$
and
![]() $Q_1,\ldots,Q_l$
are
$Q_1,\ldots,Q_l$
are
![]() $\varphi$
-irreducible. For a simple counterexample, take
$\varphi$
-irreducible. For a simple counterexample, take
![]() $l=2$
, and let
$l=2$
, and let
![]() $P_1$
and
$P_1$
and
![]() $P_2$
be any
$P_2$
be any
![]() $\varphi$
-irreducible Markov kernels, reversible with respect to a probability measure
$\varphi$
-irreducible Markov kernels, reversible with respect to a probability measure
![]() $\pi$
such that
$\pi$
such that
![]() $P_1$
efficiency-dominates
$P_1$
efficiency-dominates
![]() $P_2$
, but
$P_2$
, but
![]() $P_2$
does not efficiency-dominate
$P_2$
does not efficiency-dominate
![]() $P_1$
. Then by taking
$P_1$
. Then by taking
![]() $Q_1=P_2$
,
$Q_1=P_2$
,
![]() $Q_2=P_1$
, and
$Q_2=P_1$
, and
![]() $\alpha_1=\alpha_2=1/2$
, we have
$\alpha_1=\alpha_2=1/2$
, we have
![]() $P=1/2\left(P_1+P_2\right)$
and
$P=1/2\left(P_1+P_2\right)$
and
![]() $Q=1/2\left(Q_1+Q_2\right)=1/2\left(P_1+P_2\right)$
, so
$Q=1/2\left(Q_1+Q_2\right)=1/2\left(P_1+P_2\right)$
, so
![]() $P=Q$
. Thus, as efficiency dominance is reflexive by Theorem 4.3, P efficiency-dominates Q. However, by assumption,
$P=Q$
. Thus, as efficiency dominance is reflexive by Theorem 4.3, P efficiency-dominates Q. However, by assumption,
![]() $P_2$
does not efficiency-dominate
$P_2$
does not efficiency-dominate
![]() $P_1=Q_2$
, thus the components do not efficiency-dominate each other.
$P_1=Q_2$
, thus the components do not efficiency-dominate each other.
What is true is the following.
Corollary 5.1. Let P, Q, and R be Markov kernels reversible with respect to
![]() $\pi$
. Then for every
$\pi$
. Then for every
![]() $\alpha\in(0,1)$
, P efficiency-dominates Q if and only if
$\alpha\in(0,1)$
, P efficiency-dominates Q if and only if
![]() $\alpha P+(1-\alpha)R$
efficiency-dominates
$\alpha P+(1-\alpha)R$
efficiency-dominates
![]() $\alpha Q+(1-\alpha)R$
.
$\alpha Q+(1-\alpha)R$
.
Proof. If P efficiency-dominates Q, by Theorem 5.1,
![]() $\alpha P+(1-\alpha)R$
efficiency-dominates
$\alpha P+(1-\alpha)R$
efficiency-dominates
![]() $\alpha Q+(1-\alpha)R$
.
$\alpha Q+(1-\alpha)R$
.
If
![]() $\alpha P+(1-\alpha)R$
efficiency-dominates
$\alpha P+(1-\alpha)R$
efficiency-dominates
![]() $\alpha Q+(1-\alpha)R$
, by Theorem 4.2,
$\alpha Q+(1-\alpha)R$
, by Theorem 4.2,
so by Theorem 4.2 again, P efficiency-dominates Q.
Thus, when we swap only one component, the new combined chain efficiency-dominates the old combined chain if and only if the new component efficiency-dominates the old component.
Example 5.1. For
![]() $n\geq1$
, say we are interested in a possibly unnormalized probability density
$n\geq1$
, say we are interested in a possibly unnormalized probability density
![]() $f\,:\,\mathbf{R}^n\to[0,\infty)$
(here we assume that
$f\,:\,\mathbf{R}^n\to[0,\infty)$
(here we assume that
![]() $\mathbf{R}^n$
is equipped with the usual Borel
$\mathbf{R}^n$
is equipped with the usual Borel
![]() $\sigma$
-field and Lebesgue measure). Then recall from Example 4.2 that the random scan Gibbs sampler algorithm works by randomly choosing an axis in
$\sigma$
-field and Lebesgue measure). Then recall from Example 4.2 that the random scan Gibbs sampler algorithm works by randomly choosing an axis in
![]() $\mathbf{R}^n$
, and updating only the jth coordinate using the marginal distribution of f on that axis given the last point, i.e. given
$\mathbf{R}^n$
, and updating only the jth coordinate using the marginal distribution of f on that axis given the last point, i.e. given
![]() $x_k=(x_k^{(1)},\ldots,x_k^{(n)})\in\mathbf{R}^n$
, choose an axis
$x_k=(x_k^{(1)},\ldots,x_k^{(n)})\in\mathbf{R}^n$
, choose an axis
![]() $j\in\{1,\ldots,n\}$
uniformly at random, pick
$j\in\{1,\ldots,n\}$
uniformly at random, pick
![]() $x^{(j)}_{k+1}$
according to the one-dimensional probability distribution
$x^{(j)}_{k+1}$
according to the one-dimensional probability distribution
![]() $f_j(\!\cdot|(x^{(1)}_k,\ldots,x^{(j-1)}_k,x^{(j+1)}_k,\ldots,x^{(n)}_k)$
, where
$f_j(\!\cdot|(x^{(1)}_k,\ldots,x^{(j-1)}_k,x^{(j+1)}_k,\ldots,x^{(n)}_k)$
, where
![]() $f_j$
is the marginal distribution in the jth coordinate, and set
$f_j$
is the marginal distribution in the jth coordinate, and set
![]() $x_{k+1}=(x_k^{(1)},\ldots,x^{(j-1)}_k,x^{(j)}_{k+1},x^{(j+1)}_k,\ldots,x^{(n)}_k)$
.
$x_{k+1}=(x_k^{(1)},\ldots,x^{(j-1)}_k,x^{(j)}_{k+1},x^{(j+1)}_k,\ldots,x^{(n)}_k)$
.
For every measurable set
![]() $A\subseteq\mathbf{R}^n$
,
$A\subseteq\mathbf{R}^n$
,
![]() $x=(x^{(1)},\ldots,x^{(n)})\in\mathbf{R}^n$
and
$x=(x^{(1)},\ldots,x^{(n)})\in\mathbf{R}^n$
and
![]() $j\in\{1,\ldots,n\}$
, let
$j\in\{1,\ldots,n\}$
, let
![]() $A_j(x)\,:\!=\,\{y^{(j)}\in\mathbf{R}\,:\,(x^{(1)},\ldots,x^{(j-1)},y^{(j)},x^{(j+1)},\ldots, x^{(n)})\in A\}$
. Then this algorithm has Markov kernel
$A_j(x)\,:\!=\,\{y^{(j)}\in\mathbf{R}\,:\,(x^{(1)},\ldots,x^{(j-1)},y^{(j)},x^{(j+1)},\ldots, x^{(n)})\in A\}$
. Then this algorithm has Markov kernel
 \begin{align*}Q(x,A)=\frac{1}{n}\sum_{j=1}^nQ_j(x,A)=\frac{1}{n}\sum_{j=1}^n\frac{\int_{A_j(x)} f(x^{(1)},\ldots,x^{(j-1)},t,x^{(j+1)},\ldots,x^{(n)})dt}{\int_{\mathbf{R}}f(x^{(1)},\ldots,x^{(j-1)},t,x^{(j+1)},\ldots,x^{(n)})dt}\end{align*}
\begin{align*}Q(x,A)=\frac{1}{n}\sum_{j=1}^nQ_j(x,A)=\frac{1}{n}\sum_{j=1}^n\frac{\int_{A_j(x)} f(x^{(1)},\ldots,x^{(j-1)},t,x^{(j+1)},\ldots,x^{(n)})dt}{\int_{\mathbf{R}}f(x^{(1)},\ldots,x^{(j-1)},t,x^{(j+1)},\ldots,x^{(n)})dt}\end{align*}
for every
![]() $x\in\mathbf{R}^n$
and measurable
$x\in\mathbf{R}^n$
and measurable
![]() $A\subseteq\mathbf{R}^n$
, where
$A\subseteq\mathbf{R}^n$
, where
![]() $Q_j$
is the Markov kernel associated with updating the jth coordinate. Notice that for every
$Q_j$
is the Markov kernel associated with updating the jth coordinate. Notice that for every
![]() $j\in\{1,\ldots,n\}$
, the Markov kernel
$j\in\{1,\ldots,n\}$
, the Markov kernel
![]() $Q_j$
corresponding to updating the jth coordinate is simply i.i.d. sampling from the one-dimensional probability distribution
$Q_j$
corresponding to updating the jth coordinate is simply i.i.d. sampling from the one-dimensional probability distribution
![]() $f_j$
given the other
$f_j$
given the other
![]() $n-1$
coordinates (as described in the previous paragraph).
$n-1$
coordinates (as described in the previous paragraph).
Thus, to find a more efficient algorithm than Gibbs sampling, by Theorem 5.1, it suffices to simply find an algorithm that efficiency-dominates i.i.d. sampling in one dimension, and then the sum of this new algorithm applied to each coordinate’s marginal distribution, as described above, will efficiency-dominate Gibbs sampling. Some work in this direction can be found in [Reference Neal19] for discrete state spaces.
6. Peskun Dominance
In this section, we show that Peskun dominance implies efficiency dominance (Theorem 6.1), a result first established by Peskun [Reference Peskun21] for finite state spaces and then generalized to general state spaces by Tierney [Reference Tierney27]. As in [Reference Tierney27], we first show that if P and Q are reversible Markov kernels such that P Peskun-dominates Q, then
![]() $\mathcal{Q}-\mathcal{P}$
is a positive operator (Lemma 6.1), and we then use Theorem 4.2 to obtain the result. We then consider an important example as seen in [Reference Tierney27], and finish the section by taking another look at Example 4.3 established in Section 4 to give an easy example of Markov kernels P and Q such that P efficiency-dominates Q but P does not Peskun-dominate Q.
$\mathcal{Q}-\mathcal{P}$
is a positive operator (Lemma 6.1), and we then use Theorem 4.2 to obtain the result. We then consider an important example as seen in [Reference Tierney27], and finish the section by taking another look at Example 4.3 established in Section 4 to give an easy example of Markov kernels P and Q such that P efficiency-dominates Q but P does not Peskun-dominate Q.
We start with our key lemma.
Lemma 6.1. If P and Q are Markov kernels reversible with respect to
![]() $\pi$
such that P Peskun-dominates Q, then
$\pi$
such that P Peskun-dominates Q, then
![]() $\mathcal{Q}-\mathcal{P}$
is a positive operator.
$\mathcal{Q}-\mathcal{P}$
is a positive operator.
Proof. For every
![]() $x\in\mathbf{X}$
, let
$x\in\mathbf{X}$
, let
![]() $\delta_x:\mathcal{F}\to\{0,1\}$
be the measure such that
$\delta_x:\mathcal{F}\to\{0,1\}$
be the measure such that
 $\delta_x(E)= \begin{cases} 1,\quad x\in E\\ 0 \quad \mathrm{otherwise} \end{cases}$
for every
$\delta_x(E)= \begin{cases} 1,\quad x\in E\\ 0 \quad \mathrm{otherwise} \end{cases}$
for every
![]() $E\in\mathcal{F}$
.
$E\in\mathcal{F}$
.
Then notice that as P and Q are reversible with respect to
![]() $\pi$
,
$\pi$
,
Thus, for every
![]() $f\in L^2_0(\pi)$
, we have
$f\in L^2_0(\pi)$
, we have
 \begin{align*} \langle f,(\mathcal{Q}-\mathcal{P})f\rangle &=\iint_{x,y\in\mathbf{X}}f(x)f(y) (Q(x,\mathrm{d}y)-P(x,\mathrm{d}y))\pi(\mathrm{d}x)\\ &=\int_{x\in\mathbf{X}}f(x)^2\pi(\mathrm{d}x)\\ &\hspace{1.5cm}-\iint_{x,y\in\mathbf{X}}f(x)f(y) (\delta_x(\mathrm{d}y)+P(x,\mathrm{d}y)-Q(x,\mathrm{d}y))\pi(\mathrm{d}x)\\ &=\frac{1}{2}\iint_{x,y\in\mathbf{X}} \left(f(x)-f(y)\right)^2 \left(\delta_x(\mathrm{d}y)+P(x,\mathrm{d}y)-Q(x,\mathrm{d}y)\right)\pi(\mathrm{d}x). \end{align*}
\begin{align*} \langle f,(\mathcal{Q}-\mathcal{P})f\rangle &=\iint_{x,y\in\mathbf{X}}f(x)f(y) (Q(x,\mathrm{d}y)-P(x,\mathrm{d}y))\pi(\mathrm{d}x)\\ &=\int_{x\in\mathbf{X}}f(x)^2\pi(\mathrm{d}x)\\ &\hspace{1.5cm}-\iint_{x,y\in\mathbf{X}}f(x)f(y) (\delta_x(\mathrm{d}y)+P(x,\mathrm{d}y)-Q(x,\mathrm{d}y))\pi(\mathrm{d}x)\\ &=\frac{1}{2}\iint_{x,y\in\mathbf{X}} \left(f(x)-f(y)\right)^2 \left(\delta_x(\mathrm{d}y)+P(x,\mathrm{d}y)-Q(x,\mathrm{d}y)\right)\pi(\mathrm{d}x). \end{align*}
As P Peskun-dominates Q,
![]() $\left(\delta_x(\!\cdot\!)+P(x,\cdot)-Q(x,\cdot) \right)$
is a positive measure for
$\left(\delta_x(\!\cdot\!)+P(x,\cdot)-Q(x,\cdot) \right)$
is a positive measure for
![]() $\pi$
-almost every
$\pi$
-almost every
![]() $x\in\mathbf{X}$
. Thus,
$x\in\mathbf{X}$
. Thus,
As
![]() $f\in L^2_0(\pi)$
is arbitrary,
$f\in L^2_0(\pi)$
is arbitrary,
![]() $\mathcal{Q}-\mathcal{P}$
is a positive operator.
$\mathcal{Q}-\mathcal{P}$
is a positive operator.
Now with Theorem 4.2 we can easily show the following result from [Reference Peskun21, Reference Tierney27].
Theorem 6.1. If P and Q are Markov kernels reversible with respect to
![]() $\pi$
such that P Peskun-dominates Q, then P efficiency-dominates Q.
$\pi$
such that P Peskun-dominates Q, then P efficiency-dominates Q.
Proof. By Lemma 6.1,
![]() $\mathcal{Q}-\mathcal{P}$
is a positive operator (i.e.
$\mathcal{Q}-\mathcal{P}$
is a positive operator (i.e.
![]() $\sigma(\mathcal{Q}-\mathcal{P})\subseteq[0,\infty)$
), and thus by Theorem 4.2, P efficiency-dominates Q.
$\sigma(\mathcal{Q}-\mathcal{P})\subseteq[0,\infty)$
), and thus by Theorem 4.2, P efficiency-dominates Q.
In [Reference Tierney27], Theorem 6.1 is used to show that given a set of proposal kernels, the MH algorithm that samples from a weighted sum of the proposal kernels and then performs the accept/reject step efficiency-dominates the weighted sum of MH algorithms with said proposal kernels. We consider this example next.
Example 6.1. Say we are interested in sampling from a possibly unnormalized probability density
![]() $f\,:\,\mathbf{X}\to[0,\infty)$
on
$f\,:\,\mathbf{X}\to[0,\infty)$
on
![]() $(\mathbf{X},\mathcal{X},\mu)$
. One of the most common algorithms we can use is the MH algorithm.
$(\mathbf{X},\mathcal{X},\mu)$
. One of the most common algorithms we can use is the MH algorithm.
Let
![]() $Q(x,\mathrm{d}y)=q(x,y)\mu(\mathrm{d}y)$
be any other proposal Markov kernel that is absolutely continuous with respect to
$Q(x,\mathrm{d}y)=q(x,y)\mu(\mathrm{d}y)$
be any other proposal Markov kernel that is absolutely continuous with respect to
![]() $\mu$
. Then if
$\mu$
. Then if
![]() $\{X_k\}_{k=0}^{\infty}$
is the Markov chain run by the MH algorithm, then given
$\{X_k\}_{k=0}^{\infty}$
is the Markov chain run by the MH algorithm, then given
![]() $X_k=x\in\mathbf{X}$
, we first use
$X_k=x\in\mathbf{X}$
, we first use
![]() $Q(x,\cdot)$
to generate a sample
$Q(x,\cdot)$
to generate a sample
![]() $y\in\mathbf{X}$
, and with probability
$y\in\mathbf{X}$
, and with probability
![]() $\alpha(x,y)=\min\left\{1,\frac{f(y)q(y,x)}{f(x)q(x,y)}\right\}$
we set
$\alpha(x,y)=\min\left\{1,\frac{f(y)q(y,x)}{f(x)q(x,y)}\right\}$
we set
![]() $X_{k+1}=y$
, otherwise the chain stays at x, i.e.
$X_{k+1}=y$
, otherwise the chain stays at x, i.e.
![]() $X_{k+1}=x$
. This chain has Markov kernel
$X_{k+1}=x$
. This chain has Markov kernel
![]() $P(x,\mathrm{d}y)=\alpha(x,y)Q(x,\mathrm{d}y)+r(x)\delta_x(\mathrm{d}y)$
, where
$P(x,\mathrm{d}y)=\alpha(x,y)Q(x,\mathrm{d}y)+r(x)\delta_x(\mathrm{d}y)$
, where
![]() $r(x):=1-\int_{\mathbf{X}}\alpha(x,y)Q(x,\mathrm{d}y)$
and
$r(x):=1-\int_{\mathbf{X}}\alpha(x,y)Q(x,\mathrm{d}y)$
and
![]() $\delta_x$
is the point mass measure at
$\delta_x$
is the point mass measure at
![]() $x\in\mathbf{X}$
, i.e.
$x\in\mathbf{X}$
, i.e.
![]() $\delta_x(A)=1$
if
$\delta_x(A)=1$
if
![]() $x\in A$
and
$x\in A$
and
![]() $\delta_x(A)=0$
if
$\delta_x(A)=0$
if
![]() $x\notin A$
for every
$x\notin A$
for every
![]() $A\in\mathcal{X}$
. Thus, for every
$A\in\mathcal{X}$
. Thus, for every
![]() $x\in\mathbf{X}$
and every subset
$x\in\mathbf{X}$
and every subset
![]() $A\in\mathcal{X}$
such that
$A\in\mathcal{X}$
such that
![]() $x\notin A$
,
$x\notin A$
,
![]() $P(x,A)=\int_{y\in A}\alpha(x,y)Q(x,\mathrm{d}y)=\int_{y\in A}\alpha(x,y)q(x,y)\mu(\mathrm{d}y)$
.
$P(x,A)=\int_{y\in A}\alpha(x,y)Q(x,\mathrm{d}y)=\int_{y\in A}\alpha(x,y)q(x,y)\mu(\mathrm{d}y)$
.
When deciding on a proposal kernel Q to use, we often consider a sum of simpler kernels, i.e. given
![]() $\{Q_n\}_{n=0}^{N-1}$
and
$\{Q_n\}_{n=0}^{N-1}$
and
![]() $\{\beta_n\}_{n=0}^{N-1}$
such that
$\{\beta_n\}_{n=0}^{N-1}$
such that
![]() $\sum_{n=0}^{N-1}\beta_n=1$
, we might take
$\sum_{n=0}^{N-1}\beta_n=1$
, we might take
![]() $Q=\sum_{n=0}^{N-1}\beta_nQ_n$
. Now we have two natural options. Either we can use the MH algorithm of the kernel
$Q=\sum_{n=0}^{N-1}\beta_nQ_n$
. Now we have two natural options. Either we can use the MH algorithm of the kernel
![]() $Q=\sum\beta_nQ_n$
, where we denote the kernel of this algorithm as P, or we can use the sum of MH algorithms
$Q=\sum\beta_nQ_n$
, where we denote the kernel of this algorithm as P, or we can use the sum of MH algorithms
![]() $\sum_{n=0}^{N-1}\beta_nP_n$
, where each
$\sum_{n=0}^{N-1}\beta_nP_n$
, where each
![]() $P_n$
is the kernel arising from the MH algorithm with proposal
$P_n$
is the kernel arising from the MH algorithm with proposal
![]() $Q_n$
. We will show, as shown in [Reference Tierney27], that the MH algorithm run from the combined proposal Q, P, efficiency-dominates the sum of MH algorithms.
$Q_n$
. We will show, as shown in [Reference Tierney27], that the MH algorithm run from the combined proposal Q, P, efficiency-dominates the sum of MH algorithms.
For every
![]() $x\in\mathbf{X}$
and
$x\in\mathbf{X}$
and
![]() $A\in\mathcal{X}$
,
$A\in\mathcal{X}$
,
 \begin{align*} P(x,A\setminus\{x\})\;&=\;\int_{A\setminus\{x\}}\alpha(x,y)q(x,y)\mu(\mathrm{d}y)\\ \;&=\;\int_{A\setminus\{x\}}\min\left\{q(x,y),\left(\frac{f(y)}{f(x)}\right)q(y,x)\right\}\mu(\mathrm{d}y)\\ \;&\geq\;\int_{A\setminus\{x\}}\sum_{n=0}^{N-1}\beta_n\min\left\{q_n(x,y),\left(\frac{f(y)}{f(x)}\right)q_n(y,x)\right\}\mu(\mathrm{d}y)\\ \;&=\;\sum_{n=0}^{N-1}\beta_n\int_{A\setminus\{x\}}\alpha_n(x,y)q_n(x,y)\mu(\mathrm{d}y)\;=\;\sum_{n=0}^{N-1}\beta_nP_n(x,A\setminus\{x\}), \end{align*}
\begin{align*} P(x,A\setminus\{x\})\;&=\;\int_{A\setminus\{x\}}\alpha(x,y)q(x,y)\mu(\mathrm{d}y)\\ \;&=\;\int_{A\setminus\{x\}}\min\left\{q(x,y),\left(\frac{f(y)}{f(x)}\right)q(y,x)\right\}\mu(\mathrm{d}y)\\ \;&\geq\;\int_{A\setminus\{x\}}\sum_{n=0}^{N-1}\beta_n\min\left\{q_n(x,y),\left(\frac{f(y)}{f(x)}\right)q_n(y,x)\right\}\mu(\mathrm{d}y)\\ \;&=\;\sum_{n=0}^{N-1}\beta_n\int_{A\setminus\{x\}}\alpha_n(x,y)q_n(x,y)\mu(\mathrm{d}y)\;=\;\sum_{n=0}^{N-1}\beta_nP_n(x,A\setminus\{x\}), \end{align*}
where
![]() $\alpha(x,y)=\min\left\{1,\frac{f(y)q(y,x)}{f(x)q(x,y)}\right\}$
and
$\alpha(x,y)=\min\left\{1,\frac{f(y)q(y,x)}{f(x)q(x,y)}\right\}$
and
![]() $\alpha_n(x,y)=\min\left\{1,\frac{f(y)q_n(y,x)}{f(x)q_n(x,y)}\right\}$
are the acceptance probabilities of their respective MH algorithm.
$\alpha_n(x,y)=\min\left\{1,\frac{f(y)q_n(y,x)}{f(x)q_n(x,y)}\right\}$
are the acceptance probabilities of their respective MH algorithm.
As
![]() $A\in\mathcal{X}$
was arbitrary, P Peskun-dominates
$A\in\mathcal{X}$
was arbitrary, P Peskun-dominates
![]() $\sum_{n=0}^{N-1}\beta_nP_n$
, and thus by Theorem 6.1, P efficiency-dominates
$\sum_{n=0}^{N-1}\beta_nP_n$
, and thus by Theorem 6.1, P efficiency-dominates
![]() $\sum_{n=0}^{N-1}\beta_nP_n$
.
$\sum_{n=0}^{N-1}\beta_nP_n$
.
The converse of Theorem 6.1 is not true. In fact, we have already seen a simple example of a kernel that efficiency-dominates but does not Peskun-dominate another kernel.
Example 6.2. (Example 4.3, continued.) We have already seen that the Markov kernel P of Example 4.3 efficiency-dominates i.i.d. sampling on the interval [0,1]. It is also easy to see that P does not Peskun-dominate i.i.d. sampling.
Take, for example,
![]() $x=0\in[0,1]$
and
$x=0\in[0,1]$
and
![]() $A=[0,1/2]=L\in\mathcal{B}$
. Then as P jumps from the left half of the interval L to the right half of the interval R uniformly, as 0 is in the left half, clearly
$A=[0,1/2]=L\in\mathcal{B}$
. Then as P jumps from the left half of the interval L to the right half of the interval R uniformly, as 0 is in the left half, clearly
![]() $P(0,L\setminus\{0\})\leq P(0,L)=0$
. Conversely, as single points have zero mass in the Lebesgue measure, clearly
$P(0,L\setminus\{0\})\leq P(0,L)=0$
. Conversely, as single points have zero mass in the Lebesgue measure, clearly
![]() $M(0,L\setminus\{0\})=m(L\setminus\{0\})=m(L)=1/2$
(where M is the operator associated with i.i.d. sampling on
$M(0,L\setminus\{0\})=m(L\setminus\{0\})=m(L)=1/2$
(where M is the operator associated with i.i.d. sampling on
![]() $([0,1],\mathcal{B},m)$
).
$([0,1],\mathcal{B},m)$
).
Even in finite state spaces Peskun dominance is not a necessary condition for efficiency dominance. For a simple example in the finite state space case, see Section 7 in [Reference Neal and Rosenthal20]. Although Peskun dominance can be an easier condition to check, as is clear here, efficiency dominance is a much more general condition.
7. Functional Analysis Lemmas
We separate this section into two subsections. In the first subsection, we follow an approach parallel to that of Neal and Rosenthal [Reference Neal and Rosenthal20] in the finite case, substituting linear algebra for functional analysis where appropriate, to prove Lemma 4.1. In the second subsection, we follow the techniques of Mira and Geyer [Reference Mira and Geyer18] to prove Lemma 4.2.
7.1. Proof of Lemma 4.1
As shown in [Reference Mira and Geyer18], Lemma 4.1 follows from some more general results in [Reference Bendat and Sherman4]. However, these general results are very technical, and require much more than basic functional analysis to prove. So we present a different approach using basic functional analysis. These techniques are similar to what is done in Chapter V in [Reference Bhatia5], as presented by Neal and Rosenthal in [Reference Neal and Rosenthal20], but generalized for general Hilbert spaces rather than finite-dimensional vector spaces.
We begin with some lemmas about bounded self-adjoint linear operators on a Hilbert space
![]() $\mathbf{H}$
.
$\mathbf{H}$
.
Lemma 7.1. If X, Y, and Z are bounded linear operators on a Hilbert space
![]() $\mathbf{H}$
such that
$\mathbf{H}$
such that
![]() $\langle f,X\,f\rangle \leq\langle f, Y\,f\rangle$
for every
$\langle f,X\,f\rangle \leq\langle f, Y\,f\rangle$
for every
![]() $f\in\mathbf{H}$
, and Z is self-adjoint, then
$f\in\mathbf{H}$
, and Z is self-adjoint, then
![]() $\langle f,Z\,X\,Z\,f\rangle \leq \langle f,Z\,Y\,Z\,f\rangle$
for every
$\langle f,Z\,X\,Z\,f\rangle \leq \langle f,Z\,Y\,Z\,f\rangle$
for every
![]() $f\in\mathbf{H}$
.
$f\in\mathbf{H}$
.
Proof. For every
![]() $f\in\mathbf{H}$
,
$f\in\mathbf{H}$
,
![]() $Zf\in\mathbf{H}$
, so
$Zf\in\mathbf{H}$
, so
This is where the finite state space case differs from the general case. In the finite state space case,
![]() $L^2_0(\pi)$
is a finite-dimensional vector space, and thus to prove that
$L^2_0(\pi)$
is a finite-dimensional vector space, and thus to prove that
![]() $\langle f,T\,f\rangle\leq\langle f,N\,f\rangle$
for every
$\langle f,T\,f\rangle\leq\langle f,N\,f\rangle$
for every
![]() $f\in\mathbf{V}$
if and only if
$f\in\mathbf{V}$
if and only if
![]() $\langle f,T^{-1}f\rangle\geq\langle f,N^{-1}f\rangle$
for every
$\langle f,T^{-1}f\rangle\geq\langle f,N^{-1}f\rangle$
for every
![]() $f\in\mathbf{V}$
, when T and N are self-adjoint operators, the only additional assumption needed is that T and N are strictly positive, i.e. that for every
$f\in\mathbf{V}$
, when T and N are self-adjoint operators, the only additional assumption needed is that T and N are strictly positive, i.e. that for every
![]() $f\neq0\in\mathbf{V}$
,
$f\neq0\in\mathbf{V}$
,
![]() $\langle f,T\,f\rangle, \langle f,N\,f\rangle>0$
. This is shown by Neal and Rosenthal [20, Section 8]. However, in the general case, as
$\langle f,T\,f\rangle, \langle f,N\,f\rangle>0$
. This is shown by Neal and Rosenthal [20, Section 8]. However, in the general case, as
![]() $L^2_0(\pi)$
may not be finite-dimensional, T and N being strictly positive is not a strong enough assumption. In the general case, it is possible for T to be strictly positive and self-adjoint, but not be invertible in the bounded sense. Thus, it is possible that
$L^2_0(\pi)$
may not be finite-dimensional, T and N being strictly positive is not a strong enough assumption. In the general case, it is possible for T to be strictly positive and self-adjoint, but not be invertible in the bounded sense. Thus, it is possible that
![]() $0\in\sigma(T)$
. So we must use a slightly stronger assumption. We must assume that
$0\in\sigma(T)$
. So we must use a slightly stronger assumption. We must assume that
![]() $\sigma(T),\sigma(N)\subseteq(0,\infty)$
. In the finite case, this is equivalent to being strictly positive; however, it is stronger in general.
$\sigma(T),\sigma(N)\subseteq(0,\infty)$
. In the finite case, this is equivalent to being strictly positive; however, it is stronger in general.
The following lemma is Theorem 12.12 from [Reference Rudin24]. We present a more detailed proof below.
Lemma 7.2. If T is a normal bounded linear operator on a Hilbert space
![]() $\mathbf{H}$
, then there exists
$\mathbf{H}$
, then there exists
![]() $\delta >0$
such that
$\delta >0$
such that
![]() $\delta\left\lVert f\right\rVert\leq\left\lVert Tf\right\rVert$
for every
$\delta\left\lVert f\right\rVert\leq\left\lVert Tf\right\rVert$
for every
![]() $f\in\mathbf{H}$
if and only if T is invertible.
$f\in\mathbf{H}$
if and only if T is invertible.
Proof. For the forward implication, we will show that as T is normal, by the assumption it will follow that T is bijective, and then by the assumption once more the inverse of T is bounded.
Firstly, notice that for every
![]() $f\in\mathbf{H}$
such that
$f\in\mathbf{H}$
such that
![]() $f\neq0$
,
$f\neq0$
,
![]() $\left\lVert Tf\right\rVert\geq\delta\left\lVert f\right\rVert>0$
, so
$\left\lVert Tf\right\rVert\geq\delta\left\lVert f\right\rVert>0$
, so
![]() $Tf\neq0$
. As
$Tf\neq0$
. As
![]() $Tf\neq0$
for every
$Tf\neq0$
for every
![]() $f\neq0\in\mathbf{H}$
, T is injective.
$f\neq0\in\mathbf{H}$
, T is injective.
As T is normal and injective,
![]() $T^*$
is also injective, and as T is normal
$T^*$
is also injective, and as T is normal
![]() $\textrm{range}(T)^{\perp}\;=\;\textrm{null}(T^*)\;=\;\{0\}$
, so the range of T is dense in
$\textrm{range}(T)^{\perp}\;=\;\textrm{null}(T^*)\;=\;\{0\}$
, so the range of T is dense in
![]() $\mathbf{H}$
.
$\mathbf{H}$
.
Now we will show that the range of T is closed, and thus T is surjective as the range of T is also dense in
![]() $\mathbf{H}$
. For any
$\mathbf{H}$
. For any
![]() $f\in\overline{\textrm{range}(T)}$
, there exists
$f\in\overline{\textrm{range}(T)}$
, there exists
![]() $\{g_n\}_{n\in\mathbf{N}}\subseteq \mathbf{H}$
such that
$\{g_n\}_{n\in\mathbf{N}}\subseteq \mathbf{H}$
such that
![]() $Tg_n\to f$
. So for every
$Tg_n\to f$
. So for every
![]() $m,n\in\mathbf{N}$
, by our assumption
$m,n\in\mathbf{N}$
, by our assumption
so
![]() $\{g_n\}\subseteq\mathbf{H}$
is Cauchy as
$\{g_n\}\subseteq\mathbf{H}$
is Cauchy as
![]() $\{Tg_n\}$
converges. Thus, as
$\{Tg_n\}$
converges. Thus, as
![]() $\mathbf{H}$
is complete (as it is a Hilbert space), there exists
$\mathbf{H}$
is complete (as it is a Hilbert space), there exists
![]() $g\in\mathbf{H}$
such that
$g\in\mathbf{H}$
such that
![]() $g_n\to g$
. As T is bounded, it is also continuous, and thus
$g_n\to g$
. As T is bounded, it is also continuous, and thus
![]() $Tg_n\to Tg$
, and as the limits are unique and
$Tg_n\to Tg$
, and as the limits are unique and
![]() $Tg_n\to f$
as well,
$Tg_n\to f$
as well,
![]() $Tg=f$
and
$Tg=f$
and
![]() $f\in\textrm{range}(T)$
. So
$f\in\textrm{range}(T)$
. So
![]() $\textrm{range}(T)$
is closed.
$\textrm{range}(T)$
is closed.
So as T is bijective, there exists an operator
![]() $T^{-1}$
such that
$T^{-1}$
such that
![]() $TT^{-1}f=f$
for every
$TT^{-1}f=f$
for every
![]() $f\in\mathbf{H}$
. By our assumption, letting
$f\in\mathbf{H}$
. By our assumption, letting
![]() $C=\delta^{-1}$
, we have
$C=\delta^{-1}$
, we have
for every
![]() $f\in\mathbf{H}$
, and so
$f\in\mathbf{H}$
, and so
![]() $T^{-1}$
is bounded.
$T^{-1}$
is bounded.
For the converse, say T is invertible. Then let
![]() $\delta= \left\lVert T^{-1}\right\rVert^{-1}$
. Then for every
$\delta= \left\lVert T^{-1}\right\rVert^{-1}$
. Then for every
![]() $f\in\mathbf{H}$
, by the definition of
$f\in\mathbf{H}$
, by the definition of
![]() $\delta$
,
$\delta$
,
Remark 7.1. The assumption that T be normal in the Lemma 7.2 is only to show us that T is bijective in the ‘only if’ direction. In general, if T is a bounded linear operator, not necessarily normal, and is bijective and there exists
![]() $\delta>0$
such that
$\delta>0$
such that
![]() $\left\lVert Tf\right\rVert\geq\delta\left\lVert f\right\rVert$
for every
$\left\lVert Tf\right\rVert\geq\delta\left\lVert f\right\rVert$
for every
![]() $f\in\mathbf{H}$
, then T is invertible. Furthermore, the ‘if’ direction of Lemma 7.2 does not require that T be normal.
$f\in\mathbf{H}$
, then T is invertible. Furthermore, the ‘if’ direction of Lemma 7.2 does not require that T be normal.
Now we can prove Lemma 4.1.
Proof of Lemma 4.1. Say
![]() $\langle f,Tf\rangle\leq\langle f,Nf\rangle$
for every
$\langle f,Tf\rangle\leq\langle f,Nf\rangle$
for every
![]() $f\in\mathbf{H}$
.
$f\in\mathbf{H}$
.
As
![]() $\sigma(N)\subseteq(0,\infty)$
, N is invertible, and
$\sigma(N)\subseteq(0,\infty)$
, N is invertible, and
![]() $N^{-1/2}$
is a well-defined bounded self-adjoint linear operator. Similarly,
$N^{-1/2}$
is a well-defined bounded self-adjoint linear operator. Similarly,
![]() $T^{1/2}$
is also a well-defined bounded self-adjoint linear operator.
$T^{1/2}$
is also a well-defined bounded self-adjoint linear operator.
So, for every
![]() $f\in\mathbf{H}$
, we have
$f\in\mathbf{H}$
, we have
Furthermore, as
![]() $\sigma(T)\subseteq(0,\infty)$
, T is invertible, so by Lemma 7.2, there exists
$\sigma(T)\subseteq(0,\infty)$
, T is invertible, so by Lemma 7.2, there exists
![]() $\delta_T>0$
such that
$\delta_T>0$
such that
![]() $\left\lVert Tf\right\rVert\geq\delta_T\left\lVert f\right\rVert$
for every
$\left\lVert Tf\right\rVert\geq\delta_T\left\lVert f\right\rVert$
for every
![]() $f\in\mathbf{H}$
. Also, notice that
$f\in\mathbf{H}$
. Also, notice that
![]() $\sigma(N^{-1/2})\subseteq(0,\infty)$
; thus, by Lemma 7.2, there exists
$\sigma(N^{-1/2})\subseteq(0,\infty)$
; thus, by Lemma 7.2, there exists
![]() $\delta_1>0$
such that
$\delta_1>0$
such that
![]() $\left\lVert N^{-1/2}f\right\rVert\geq\delta_1\left\lVert f\right\rVert$
for every
$\left\lVert N^{-1/2}f\right\rVert\geq\delta_1\left\lVert f\right\rVert$
for every
![]() $f\in\mathbf{H}$
. So, for every
$f\in\mathbf{H}$
. So, for every
![]() $f\in\mathbf{H}$
,
$f\in\mathbf{H}$
,
so by Lemma 7.2,
![]() $N^{-1/2}TN^{-1/2}$
is invertible, and thus
$N^{-1/2}TN^{-1/2}$
is invertible, and thus
![]() $0\not\in\sigma(N^{-1/2}TN^{-1/2})$
.
$0\not\in\sigma(N^{-1/2}TN^{-1/2})$
.
By using Lemma 7.1 with
![]() $X=T$
,
$X=T$
,
![]() $Y=N$
, and
$Y=N$
, and
![]() $Z=N^{-1/2}$
, for every
$Z=N^{-1/2}$
, for every
![]() $f\in\mathbf{H}$
, we have
$f\in\mathbf{H}$
, we have
So if
![]() $\lambda>1$
, for any
$\lambda>1$
, for any
![]() $f\in\mathbf{H}$
, as
$f\in\mathbf{H}$
, as
![]() $0\leq \langle N^{-1/2}TN^{-1/2}f,f\rangle\leq\left\lVert f\right\rVert^2$
, by the Cauchy–Schwarz inequality,
$0\leq \langle N^{-1/2}TN^{-1/2}f,f\rangle\leq\left\lVert f\right\rVert^2$
, by the Cauchy–Schwarz inequality,
![]() $\left\lVert(N^{-1/2}TN^{-1/2}-\lambda)f\right\rVert\geq|1-\lambda|\left\lVert f\right\rVert$
, and as
$\left\lVert(N^{-1/2}TN^{-1/2}-\lambda)f\right\rVert\geq|1-\lambda|\left\lVert f\right\rVert$
, and as
![]() $|1-\lambda|>0$
, by Lemma 7.2,
$|1-\lambda|>0$
, by Lemma 7.2,
![]() $(N^{-1/2}TN^{-1/2}-\lambda)$
is invertible, so
$(N^{-1/2}TN^{-1/2}-\lambda)$
is invertible, so
![]() $\lambda\not\in\sigma(N^{-1/2}TN^{-1/2})$
. Thus, we have
$\lambda\not\in\sigma(N^{-1/2}TN^{-1/2})$
. Thus, we have
![]() $\sigma(N^{-1/2}TN^{-1/2})\subseteq(0,1]$
.
$\sigma(N^{-1/2}TN^{-1/2})\subseteq(0,1]$
.
Let K denote the inverse of
![]() $N^{-1/2}TN^{-1/2}$
, i.e. let
$N^{-1/2}TN^{-1/2}$
, i.e. let
![]() $K=(N^{-1/2}TN^{-1/2})^{-1}$
. Furthermore, we have
$K=(N^{-1/2}TN^{-1/2})^{-1}$
. Furthermore, we have
![]() $\sigma(K)\subseteq[1,\infty)$
. So for every
$\sigma(K)\subseteq[1,\infty)$
. So for every
![]() $f\in\mathbf{H}$
,
$f\in\mathbf{H}$
,
![]() $\left\lVert f\right\rVert^2\leq\langle f,Kf\rangle$
.
$\left\lVert f\right\rVert^2\leq\langle f,Kf\rangle$
.
By using Lemma 7.1, with
![]() $X=\mathcal{I}$
,
$X=\mathcal{I}$
,
![]() $Y=K$
and
$Y=K$
and
![]() $Z=N^{-1/2}$
, for every
$Z=N^{-1/2}$
, for every
![]() $f\in\mathbf{H}$
, we have
$f\in\mathbf{H}$
, we have
 \begin{align*} \langle f,N^{-1}f\rangle &=\langle f,N^{-1/2}\mathcal{I} N^{-1/2}f\rangle\\ &\leq\langle f,N^{-1/2}K N^{-1/2}f\rangle\\ &=\langle f,N^{-1/2}(N^{-1/2}TN^{-1/2})^{-1} N^{-1/2}f\rangle\\ &=\langle f,N^{-1/2}N^{1/2}T^{-1}N^{1/2} N^{-1/2}f\rangle\\ &=\langle f,T^{-1}f\rangle. \end{align*}
\begin{align*} \langle f,N^{-1}f\rangle &=\langle f,N^{-1/2}\mathcal{I} N^{-1/2}f\rangle\\ &\leq\langle f,N^{-1/2}K N^{-1/2}f\rangle\\ &=\langle f,N^{-1/2}(N^{-1/2}TN^{-1/2})^{-1} N^{-1/2}f\rangle\\ &=\langle f,N^{-1/2}N^{1/2}T^{-1}N^{1/2} N^{-1/2}f\rangle\\ &=\langle f,T^{-1}f\rangle. \end{align*}
For the other direction, replace N with
![]() $T^{-1}$
and T with
$T^{-1}$
and T with
![]() $N^{-1}$
.
$N^{-1}$
.
7.2. Proof of Lemma 4.2
Here we follow the same steps as in [Reference Mira and Geyer18] to prove Lemma 4.2.
Lemma 7.3. If T is a self-adjoint, injective, positive, and bounded operator on the Hilbert space
![]() $\mathbf{H}$
, then
$\mathbf{H}$
, then
![]() $\,{domain}\,(T^{-1})\subseteq\,{domain}\,(T^{-1/2})$
.
$\,{domain}\,(T^{-1})\subseteq\,{domain}\,(T^{-1/2})$
.
Proof. Let
![]() $f\in\textrm{domain}(T^{-1})=\textrm{range}(T)$
. Then there exists
$f\in\textrm{domain}(T^{-1})=\textrm{range}(T)$
. Then there exists
![]() $g\in\mathbf{H}$
such that
$g\in\mathbf{H}$
such that
![]() $Tg=f$
. So, as T is positive,
$Tg=f$
. So, as T is positive,
![]() $T^{1/2}$
is well-defined, so
$T^{1/2}$
is well-defined, so
![]() $T^{1/2}g=h\in\mathbf{H}$
. Notice that
$T^{1/2}g=h\in\mathbf{H}$
. Notice that
![]() $T^{1/2}h=T^{1/2}T^{1/2}g=Tg=f$
, so
$T^{1/2}h=T^{1/2}T^{1/2}g=Tg=f$
, so
![]() $f\in\textrm{range}(T^{1/2}) =\textrm{domain}(T^{-1/2})$
.
$f\in\textrm{range}(T^{1/2}) =\textrm{domain}(T^{-1/2})$
.
The next lemma is a generalization of Lemma 3.1 in [Reference Mira and Geyer18] from real Hilbert spaces to possibly complex ones. This generalization is simple but unnecessary for us, as we are dealing with real Hilbert spaces anyway.
Lemma 7.4. If T is a self-adjoint, injective, positive, and bounded linear operator on the Hilbert space
![]() $\mathbf{H}$
, then for every
$\mathbf{H}$
, then for every
![]() $f\in\mathbf{H}$
,
$f\in\mathbf{H}$
,
Proof. As T is injective and self-adjoint, the inverse of T,
![]() $T^{-1}\,:\,\textrm{range}(T)\to\mathbf{H}$
, is densely defined and self-adjoint (see Proposition X.2.4(b) in [Reference Conway6]).
$T^{-1}\,:\,\textrm{range}(T)\to\mathbf{H}$
, is densely defined and self-adjoint (see Proposition X.2.4(b) in [Reference Conway6]).
For every
![]() $f\in\textrm{range}(T)=\textrm{domain}(T^{-1})$
, there exists
$f\in\textrm{range}(T)=\textrm{domain}(T^{-1})$
, there exists
![]() $g\in\mathbf{H}$
such that
$g\in\mathbf{H}$
such that
![]() $Tg=f$
. Thus, as T is positive and self-adjoint,
$Tg=f$
. Thus, as T is positive and self-adjoint,
so
![]() $T^{-1}$
is also positive. In particular, this means that
$T^{-1}$
is also positive. In particular, this means that
![]() $T^{1/2}$
and
$T^{1/2}$
and
![]() $T^{-1/2}$
are well-defined.
$T^{-1/2}$
are well-defined.
By Lemma 7.3,
![]() $\textrm{domain}(T^{-1})\subseteq\textrm{domain}(T^{-1/2})$
. Let
$\textrm{domain}(T^{-1})\subseteq\textrm{domain}(T^{-1/2})$
. Let
![]() $f\in\mathbf{H}$
and let
$f\in\mathbf{H}$
and let
![]() $h=Tf$
. Then for every
$h=Tf$
. Then for every
![]() $g\in\textrm{domain}(T^{-1/2})= \textrm{range}(T^{1/2})$
,
$g\in\textrm{domain}(T^{-1/2})= \textrm{range}(T^{1/2})$
,
 \begin{align*} \langle f,&Tf\rangle-\left(\langle g,f\rangle+\langle f,g\rangle -\langle T^{-1/2}g,T^{-1/2}g\rangle\right)\\ &=\langle T^{1/2}f,T^{1/2}f\rangle-\langle g,T^{-1}h\rangle -\langle T^{-1}h,g\rangle +\langle T^{-1/2}g,T^{-1/2}g\rangle\\ &=\langle T^{-1/2}h,T^{-1/2}h\rangle-\langle T^{-1/2}g, T^{-1/2}h\rangle-\langle T^{-1/2}h,T^{-1/2}g\rangle +\langle T^{-1/2}g,T^{-1/2}g\rangle\\ &=\langle T^{-1/2}(h-g),T^{-1/2}(h-g)\rangle\\ &=\left\lVert T^{-1/2}(h-g)\right\rVert^2\\ &\geq0. \end{align*}
\begin{align*} \langle f,&Tf\rangle-\left(\langle g,f\rangle+\langle f,g\rangle -\langle T^{-1/2}g,T^{-1/2}g\rangle\right)\\ &=\langle T^{1/2}f,T^{1/2}f\rangle-\langle g,T^{-1}h\rangle -\langle T^{-1}h,g\rangle +\langle T^{-1/2}g,T^{-1/2}g\rangle\\ &=\langle T^{-1/2}h,T^{-1/2}h\rangle-\langle T^{-1/2}g, T^{-1/2}h\rangle-\langle T^{-1/2}h,T^{-1/2}g\rangle +\langle T^{-1/2}g,T^{-1/2}g\rangle\\ &=\langle T^{-1/2}(h-g),T^{-1/2}(h-g)\rangle\\ &=\left\lVert T^{-1/2}(h-g)\right\rVert^2\\ &\geq0. \end{align*}
As
![]() $h\in\textrm{domain}(T^{-1})$
and
$h\in\textrm{domain}(T^{-1})$
and
![]() $\textrm{domain}(T^{-1})\subseteq \textrm{domain}(T^{-1/2})$
,
$\textrm{domain}(T^{-1})\subseteq \textrm{domain}(T^{-1/2})$
,
![]() $h\in\textrm{domain}(T^{-1/2})$
. So, as T is self-adjoint,
$h\in\textrm{domain}(T^{-1/2})$
. So, as T is self-adjoint,
With Lemma 7.4 established, the proof of Lemma 4.2 is straightforward.
Proof of Lemma
4.2. Let
![]() $f\in\mathbf{H}$
. Then by Lemma 7.4,
$f\in\mathbf{H}$
. Then by Lemma 7.4,
 \begin{align*} \langle f,Tf\rangle &=\sup_{g\in\textrm{domain}(T^{-1/2})}\langle g,f\rangle+\langle f,g\rangle -\langle T^{-1/2}g,T^{-1/2}g\rangle\\ &\leq\sup_{g\in\textrm{domain}(N^{-1/2})}\langle g,f\rangle+ \langle f,g\rangle -\langle N^{-1/2}g,N^{-1/2}g\rangle\\ &=\langle f,Nf\rangle.\\[-38pt] \end{align*}
\begin{align*} \langle f,Tf\rangle &=\sup_{g\in\textrm{domain}(T^{-1/2})}\langle g,f\rangle+\langle f,g\rangle -\langle T^{-1/2}g,T^{-1/2}g\rangle\\ &\leq\sup_{g\in\textrm{domain}(N^{-1/2})}\langle g,f\rangle+ \langle f,g\rangle -\langle N^{-1/2}g,N^{-1/2}g\rangle\\ &=\langle f,Nf\rangle.\\[-38pt] \end{align*}
Acknowledgements
We thank Austin Brown and Heydar Radjavi for some very helpful discussions about the spectral theorem which allowed us to prove Lemma 4.3. We also thank the editor and the reviewers for their valuable comments and input, from which this paper benefited substantially.
Funding information
This work was partially funded by NSERC of Canada.
Competing interests
There were no competing interests to declare which arose during the preparation or publication process for this article.