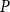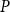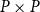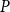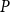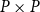Domains exhibit a variety of different aspects, some are order theoretical, some are topological, some belong to topological algebra. In this paper, we introduce two kinds of congruence relations on domains: I-congruence relation and II-congruence relation on domains. We obtain that there is a bijection from the set of all kernel operators of domain 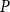$P$ preserving directed sups onto the set of all I-congruence relations on 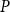$P$ which exclude 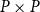$P\times P$. There is also a bijection from the set of all closure operators of domain 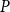$P$ preserving directed sups onto the set of all II-congruence relations on 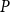$P$ which exclude 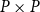$P\times P$. Furthermore, between two domains, we propose a new homomorphism called I-homomorphism and II-homomorphism, respectively. We conclude that the kernels of I-homomorphisms and II-homomorphisms between domains are I-congruence relations and II-congruence relations on domains, respectively. Therefore, we obtain the I-homomorphism and I-isomorphism theorems, as well as II-homomorphism and II-isomorphism theorems for domains. Besides, we give a positive answer to an open problem on homomorphisms and quotients of continuous semilattices posed by G. Gierz, et al.