No CrossRef data available.
Article contents
Congruence relations on domains
Published online by Cambridge University Press: 02 January 2026
Abstract
Domains exhibit a variety of different aspects, some are order theoretical, some are topological, some belong to topological algebra. In this paper, we introduce two kinds of congruence relations on domains: I-congruence relation and II-congruence relation on domains. We obtain that there is a bijection from the set of all kernel operators of domain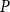 
$P$ preserving directed sups onto the set of all I-congruence relations on 
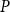$P$ which exclude 
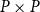$P\times P$. There is also a bijection from the set of all closure operators of domain 
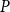$P$ preserving directed sups onto the set of all II-congruence relations on 
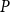$P$ which exclude 
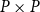$P\times P$. Furthermore, between two domains, we propose a new homomorphism called I-homomorphism and II-homomorphism, respectively. We conclude that the kernels of I-homomorphisms and II-homomorphisms between domains are I-congruence relations and II-congruence relations on domains, respectively. Therefore, we obtain the I-homomorphism and I-isomorphism theorems, as well as II-homomorphism and II-isomorphism theorems for domains. Besides, we give a positive answer to an open problem on homomorphisms and quotients of continuous semilattices posed by G. Gierz, et al.
Keywords
Information
- Type
- Paper
- Information
- Copyright
- © The Author(s), 2025. Published by Cambridge University Press
Footnotes
*
This work is supported by the National Natural Science Foundation of China (Nos. 12231007, 12501638, 12571498) and by Natural Science Foundation of Henan Province (No. 252300420896).
References
Blyth, T. S. and Janowitz, M. F. (1972). Residuation Theory, vol. 102 of International Series of Monographs in Pure and Applied Mathematics, Pergamon Press.Google Scholar
Chajda, I. and Snášel, V. (1998). Congruences in ordered sets. Mathematica Bohemica 123 95–100.CrossRefGoogle Scholar
Chajda, I., Snášel, V. and Jukl, M. (2009). Congruences in ordered sets and LU compatible equivalences, Acta Universitatis Palackianae Olomucensis. Facultas Rerum Naturalium. Mathematica 48 153–156.Google Scholar
Davey, B. A. and Priestley, H. A. (2002). Introduction to Lattices and Order, Second edn. Cambridge University Press.CrossRefGoogle Scholar
Fiech, A. (1996). Colimits in the category DCPO. Mathmetical Structures in Computer Science 6 455–468.CrossRefGoogle Scholar
Gierz, G., Hofmann, K. H., Keimel, K., Lawson, J. D., Mislove, M. and Scott, D. S. (2003). Continuous lattices and domains, vol. 93 of Encyclopedia of Mathematics and its Applications, Cambridge University Press.CrossRefGoogle Scholar
Goubault-Larrecq, J. (2013). Non-Hausdorff Topology and Domain Theory, vol. 22 of New Mathematical Monographs, Cambridge University Press.CrossRefGoogle Scholar
Hofmann, K. H. and Mislove, M. W. (1977). The lattice of kernel operators and topological algebra. Mathematische Zeitschrift 154) 175–188.CrossRefGoogle Scholar
Jin, M. and Li, Q. (2022). Quotients of L-domains. Journal of Pure and Applied Algebra 226 106837.CrossRefGoogle Scholar
Jung, A., Libkin, L. and Puhlmann, H. (1992). Decomposition of domains. In: Proceedings of the Conference on Mathematical Foundations of Programming Semantics 91, Lecture Notes in Computer Science, vol. 598, 235–258.CrossRefGoogle Scholar
Kolibiar, M. (1987). Congruence relations and direct decomposition of ordered sets, Acta Universitatis Szegediensis. Acta Scientiarum Mathematicarum 51 129–135.Google Scholar
Mahmoudi, M., Moghbeli, H. and Pióro, K. (2017). Natural congruences and isomorphism theorems for directed complete partially ordered sets. Algebra Universalis 77 (1) 79–99.CrossRefGoogle Scholar
Mahmoudi, M., Moghbeli, H. and Pióro, K. (2019). Directed complete poset congruences. Journal of Pure and Applied Algebra 223 4161–4170.CrossRefGoogle Scholar
Shum, K. P., Zhu, P. and Kehayopulu, N. (2008). III-Homomorphisms and III-congruences on posets. Discrete Mathematics 308 5006–5013.CrossRefGoogle Scholar