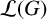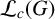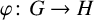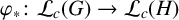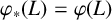Refine search
Actions for selected content:
1 results
A NOTE ON THE OPEN MAPPINGS OF LOCALLY COMPACT GROUPS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society , First View
- Published online by Cambridge University Press:
- 11 November 2025, pp. 1-8
-
- Article
- Export citation
-
Let G be a locally compact topological group and
$\mathcal {L}(G)$ the space of all its closed subgroups endowed with the Vietoris topology. Let 
$\mathcal {L}_c(G)$ be the subspace of all compact subgroups of G. Any continuous morphism 
$\varphi \colon G\to H$ between locally compact groups G and H functorially induces a continuous map 
$\varphi _*\colon \mathcal {L}_c(G)\to \mathcal {L}_c(H)$ given by 
$\varphi _*(L)=\varphi (L)$. The main problem addressed in this paper is that of determining the relationship between the openness of 
$\varphi $ and the openness of 
$\varphi _*$. For example, we show that if G is locally compact with compact identity component and H is locally compact and totally disconnected, then 
$\varphi $ is open if and only if 
$\varphi _*$ is open.
