Hostname: page-component-857557d7f7-8wkb5 Total loading time: 0 Render date: 2025-11-22T08:13:05.634Z Has data issue: false hasContentIssue false
  • English
  • Français

A NOTE ON THE OPEN MAPPINGS OF LOCALLY COMPACT GROUPS

Part of: Locally compact groups and their algebras

Published online by Cambridge University Press:  11 November 2025

ZOUHOUR JLALI Open the ORCID record for ZOUHOUR JLALI [Opens in a new window]
ZOUHOUR JLALI*
Affiliation:
Department of Mathematics, Faculty of Sciences at Sfax, Sfax University , B.P. 1171. 3000 Sfax, Tunisia
*
e-mail: zouhourjlali2@gmail.com
Get access Rights & Permissions [Opens in a new window]

Abstract

Let G be a locally compact topological group and 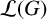$\mathcal {L}(G)$ the space of all its closed subgroups endowed with the Vietoris topology. Let 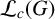$\mathcal {L}_c(G)$ be the subspace of all compact subgroups of G. Any continuous morphism 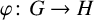$\varphi \colon G\to H$ between locally compact groups G and H functorially induces a continuous map 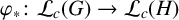$\varphi _*\colon \mathcal {L}_c(G)\to \mathcal {L}_c(H)$ given by 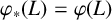$\varphi _*(L)=\varphi (L)$. The main problem addressed in this paper is that of determining the relationship between the openness of 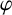$\varphi $ and the openness of 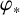$\varphi _*$. For example, we show that if G is locally compact with compact identity component and H is locally compact and totally disconnected, then 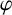$\varphi $ is open if and only if 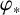$\varphi _*$ is open.

Keywords

locally compact groupidentity componentcompactly ruled grouptotally disconnected groupcompact subgroupopen mapping theoremVietoris topology

MSC classification

Primary: 22D05: General properties and structure of locally compact groups

Information

Type
Research Article
Information
Bulletin of the Australian Mathematical Society , First View , pp. 1 - 8
Check for updates
Copyright
© The Author(s), 2025. Published by Cambridge University Press on behalf of Australian Mathematical Publishing Association Inc

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Cowling, M. G., Hofmann, K. H. and Morris, S. A., ‘Open mappings of locally compact groups’, J. Group Theory 27 (2024), 1143–1149.Google Scholar
Csikós, B., Kátay, T., Kocsis, A. and Pálfy, M., ‘Compact Lie groups isolated up to conjugacy’, Preprint, 2022, arXiv:2209.15389.Google Scholar
Djocovic, D. Z., ‘The union of compact subgroups of a connected locally compact group’, Math. Z. 158 (1978), 99–105.10.1007/BF01320860CrossRefGoogle Scholar
Donjuán, V., Jonard-Pérez, N. and López-Poo, A., ‘Some notes on induced functions and group actions on hyperspaces’, Topol. Appl. 311 (2022), Article no. 107954.10.1016/j.topol.2021.107954CrossRefGoogle Scholar
Fisher, S. and Gartside, P., ‘On the space of subgroups of a compact group II’, Topol. Appl. 156 (2009), 855–861.10.1016/j.topol.2008.11.004CrossRefGoogle Scholar
Gartside, P. and Smith, M., ‘Classifying spaces of subgroups of profinite groups’, J. Group Theory 13 (2010), 315–336.Google Scholar
Hamrouni, H. and Jlali, Z., ‘A characterization of totally disconnected compactly ruled groups’, Proc. Math. Sci. 131 (2021), 1–10.10.1007/s12044-020-00601-8CrossRefGoogle Scholar
Herfort, W., Hofmann, K. H. and Russo, F. G., Periodic Locally Compact Groups, De Gruyter Studies in Mathematics, 71 (De Gruyter, Berlin, 2019).Google Scholar
Hofmann, K. H., ‘Locally compact semigroups in which a subgroup with compact complement is dense’, Trans. Amer. Math. Soc. 106 (1963), 19–51.10.1090/S0002-9947-1963-0144319-2CrossRefGoogle Scholar
Hofmann, K. H. and Morris, S. A., ‘Open mapping theorem for topological groups’, Topology Proc. 31 (2007), 533–551.Google Scholar
Kadri, B., ‘A characterization of compactly ruled groups’, Monatsh. Math. 207 (2025), 293–300.10.1007/s00605-024-02054-xCrossRefGoogle Scholar
Protasov, I. V., ‘Topological groups with compact lattice of closed subgroups’, Sib. Math. J. 20 (1979), 270–275.10.1007/BF00970034CrossRefGoogle Scholar
Protasov, I. V., ‘Limits of compact subgroups of a topological groups’, Dopov. AN Ukrain. SSR. Ser. A N5 (1986), 64–66.Google Scholar
Protasov, I. V., ‘Souslin number of the space of subgroups of a locally compact group’, Ukr. Math. J. 40 (1988), 559–562.10.1007/BF01057543CrossRefGoogle Scholar
Protasov, I. V., ‘Selective survey on spaces of closed subgroups of topological groups’, Axioms 7(4) (2018), Article no. 75.10.3390/axioms7040075CrossRefGoogle Scholar
Stroppel, M., Locally Compact Groups, EMS Textbooks in Mathematics (European Mathematical Society (EMS), Zürich, 2006).10.4171/016CrossRefGoogle Scholar
Wang, S. P., ‘On the Limit of subgroups in a group’, Amer. J. Math. 92 (1970), 708–724.10.2307/2373369CrossRefGoogle Scholar
Willis, G., ‘The structure of totally disconnected locally compact groups’, Math. Ann. 300 (1994), 341–363.10.1007/BF01450491CrossRefGoogle Scholar