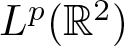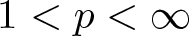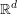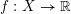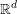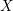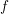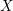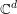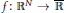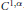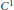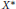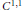Refine search
Actions for selected content:
14 results
Perron’s capacity of random sets
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 66 / Issue 4 / November 2023
- Published online by Cambridge University Press:
- 01 September 2023, pp. 960-970
-
- Article
- Export citation
ON SEPARATE CONTINUITY AND SEPARATE CONVEXITY: A SYNTHETIC TREATMENT FOR FUNCTIONS AND SETS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 109 / Issue 3 / June 2024
- Published online by Cambridge University Press:
- 17 July 2023, pp. 541-551
- Print publication:
- June 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A dichotomy of sets via typical differentiability
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 8 / 2020
- Published online by Cambridge University Press:
- 04 November 2020, e41
-
- Article
-
- You have access
- Open access
- Export citation
AN ALTERNATIVE APPROACH TO FRÉCHET DERIVATIVES
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 111 / Issue 2 / October 2021
- Published online by Cambridge University Press:
- 14 May 2020, pp. 202-220
- Print publication:
- October 2021
-
- Article
- Export citation
Arc-smooth functions on closed sets
- Part of
-
- Journal:
- Compositio Mathematica / Volume 155 / Issue 4 / April 2019
- Published online by Cambridge University Press:
- 15 March 2019, pp. 645-680
- Print publication:
- April 2019
-
- Article
- Export citation
On Whitney-type Characterization of Approximate Differentiability on Metric Measure Spaces
-
- Journal:
- Canadian Journal of Mathematics / Volume 66 / Issue 4 / 01 August 2014
- Published online by Cambridge University Press:
- 20 November 2018, pp. 721-742
- Print publication:
- 01 August 2014
-
- Article
-
- You have access
- Export citation
Quasiconvexity and Density Topology
-
- Journal:
- Canadian Mathematical Bulletin / Volume 57 / Issue 1 / 14 March 2014
- Published online by Cambridge University Press:
- 20 November 2018, pp. 178-187
- Print publication:
- 14 March 2014
-
- Article
-
- You have access
- Export citation
Monotonically Controlled Mappings
-
- Journal:
- Canadian Journal of Mathematics / Volume 63 / Issue 2 / 01 April 2011
- Published online by Cambridge University Press:
- 20 November 2018, pp. 460-480
- Print publication:
- 01 April 2011
-
- Article
-
- You have access
- Export citation
Bump Functions with Hölder Derivatives
-
- Journal:
- Canadian Journal of Mathematics / Volume 56 / Issue 4 / 01 August 2004
- Published online by Cambridge University Press:
- 20 November 2018, pp. 699-715
- Print publication:
- 01 August 2004
-
- Article
-
- You have access
- Export citation
Differentiability Properties of Optimal Value Functions
-
- Journal:
- Canadian Journal of Mathematics / Volume 56 / Issue 4 / 01 August 2004
- Published online by Cambridge University Press:
- 20 November 2018, pp. 825-842
- Print publication:
- 01 August 2004
-
- Article
-
- You have access
- Export citation
The Multidirectional Mean Value Theorem in Banach Spaces
-
- Journal:
- Canadian Mathematical Bulletin / Volume 40 / Issue 1 / 01 March 1997
- Published online by Cambridge University Press:
- 20 November 2018, pp. 88-102
- Print publication:
- 01 March 1997
-
- Article
-
- You have access
- Export citation
Subgradient Criteria for Monotonicity, The Lipschitz Condition, and Convexity
-
- Journal:
- Canadian Journal of Mathematics / Volume 45 / Issue 6 / 01 December 1993
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1167-1183
- Print publication:
- 01 December 1993
-
- Article
-
- You have access
- Export citation
Multidimensional Iterative Interpolation
-
- Journal:
- Canadian Journal of Mathematics / Volume 43 / Issue 2 / 01 April 1991
- Published online by Cambridge University Press:
- 20 November 2018, pp. 297-312
- Print publication:
- 01 April 1991
-
- Article
-
- You have access
- Export citation
The Proximal Subgradient Formula in Banach Space
-
- Journal:
- Canadian Mathematical Bulletin / Volume 31 / Issue 3 / 01 September 1988
- Published online by Cambridge University Press:
- 20 November 2018, pp. 353-361
- Print publication:
- 01 September 1988
-
- Article
-
- You have access
- Export citation