No CrossRef data available.
Article contents
Monotonically Controlled Mappings
Published online by Cambridge University Press: 20 November 2018
Abstract
Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.
We study classes of mappings between finite and infinite dimensional Banach spaces that are monotone and mappings which are differences of monotone mappings (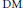 
$\text{DM}$ ). We prove a Radó–Reichelderfer estimate for monotone mappings in finite dimensional spaces that remains valid for 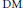$\text{DM}$ mappings. This provides an alternative proof of the Fréchet differentiability a.e. of 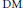$\text{DM}$ mappings. We establish a Morrey-type estimate for the distributional derivative of monotone mappings. We prove that a locally 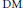$\text{DM}$ mapping between finite dimensional spaces is also globally 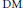$\text{DM}$ . We introduce and study a new class of the so-called 
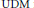$\text{UDM}$ mappings between Banach spaces, which generalizes the concept of curves of finite variation.
Keywords
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Canadian Mathematical Society 2012
References
[1]
Alberti, G. and Ambrosio, L., A geometrical approach to monotone functions in
Rn. Math. Z.
230(1999), no. 2, 259–316. doi:10.1007/PL00004691Google Scholar
[2]
Ambrosio, L., Fusco, N., and Palara, D., Functions of bounded variation and free discontinuity problems. Oxford Mathematical Monographs, The Clarendon Press, Oxford University Press, New York, 2000.Google Scholar
[3]
Bongiorno, D., A regularity condition in Sobolev spaces W1,p loc (Rn) with 1 ・ p < n. Illinois J. Math. 46(2002), no. 2, 557–570.Google Scholar
[4]
Csörnyei, M., Absolutely continuous functions of Radó, Reichelderfer, and Maly.
J. Math. Anal. Appl.
252(2000), no. 1, 147–166. doi:10.1006/jmaa.2000.6962Google Scholar
[5]
Duda, J., Metric and w¤-differentiability of pointwise Lipschitz mappings. Z. Anal. Anwend 26(2007), no. 3, 341–362. doi:10.4171/ZAA/1328Google Scholar
[6]
Duda, J., Vesel y, L. , and L. Zajıček, On d.c. functions and mappings.
Atti Sem. Mat. Fis. Univ. Modena
51(2003), no. 1, 111–138.Google Scholar
[7]
Hartman, P., On functions representable as a difference of convex functions.
Pacific J. Math.
9(1959), 707–713.Google Scholar
[8]
Kovalev, L., Quasiconformal geometry of strictly monotone mappings.
J. Lond. Math. Soc.
75(2007), no. 2, 391–408. doi:10.1112/jlms/jdm008Google Scholar
[9]
Kufner, A., John, O., and Fučık, S., Function spaces.
Monographs and Textbooks on Mechanics of Solids and Fluids; Mechanics: Analysis, Noordhoff International Publishing, Leyden; Academia, Prague, 1977.Google Scholar
[10]
Maly, J., Lectures on change of variables in integral.
http://www.math.helsinki.fi/-analysis/GraduateSchool/maly/gs.pdf.
Google Scholar
[11]
Maly, J., Absolutely continuous functions of several variables.
J. Math. Anal. Appl.
231(1999), no. 2, 492–508. doi:10.1006/jmaa.1998.6246Google Scholar
[12]
Mignot, F., Controle dans les inéquations variatonelles elliptiques.
J. Functional Analysis
22(1976), no. 2, 130–185. doi:10.1016/0022-1236(76)90017-3Google Scholar
[13]
Minty, G. J., Monotone (nonlinear) operators in Hilbert space.
Duke Math. J.
29(1962), 341–346. doi:10.1215/S0012-7094-62-02933-2Google Scholar
[14]
Phelps, R. R., Lectures on maximal monotone operators.
Extracta Math.
12(1997), no. 3, 193–230.Google Scholar
[15]
Rado, T., Reichelderfer, P. V., Continuous transformations in analysis.
Springer-Verlag, Berlin-Göttingen-Heidelberg, 1955.Google Scholar
[16]
Rudin, W., Real and complex analysis.
McGraw-Hill Book Co., New York-Toronto-London, 1966.Google Scholar
[17]
Veselý, L. and Zajίček, L., Delta-convex mappings between Banach spaces and applications. Dissertationes Math. (Rozprawy Mat.) 289(1989), 1–52.Google Scholar
You have
Access