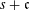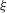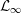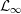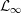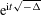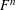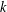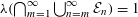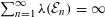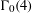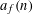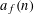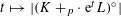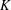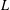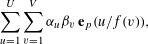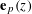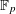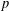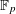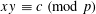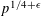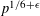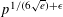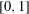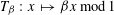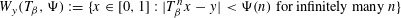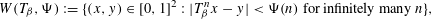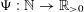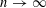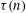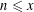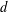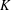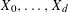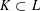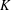Contents
Research Article
A GENERALIZATION OF THE DISCRETE VERSION OF MINKOWSKI’S FUNDAMENTAL THEOREM
- Part of:
-
- Published online by Cambridge University Press:
- 29 February 2016, pp. 637-652
-
- Article
- Export citation
INTERMEDIATE SUMS ON POLYHEDRA II: BIDEGREE AND POISSON FORMULA
- Part of:
-
- Published online by Cambridge University Press:
- 29 February 2016, pp. 653-684
-
- Article
- Export citation
ON THE STRUCTURE OF SEPARABLE
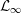 ${\mathcal{L}}_{\infty }$ -SPACES
${\mathcal{L}}_{\infty }$ -SPACES
- Part of:
-
- Published online by Cambridge University Press:
- 07 March 2016, pp. 685-700
-
- Article
- Export citation
SPECTRAL THEORETIC CHARACTERIZATION OF THE MASSLESS DIRAC ACTION
- Part of:
-
- Published online by Cambridge University Press:
- 08 March 2016, pp. 701-718
-
- Article
-
- You have access
- Open access
- Export citation
SOME SHARP BILINEAR SPACE–TIME ESTIMATES FOR THE WAVE EQUATION
- Part of:
-
- Published online by Cambridge University Press:
- 07 March 2016, pp. 719-737
-
- Article
- Export citation
UNIONS OF LINES IN
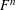 $F^{n}$
$F^{n}$
- Part of:
-
- Published online by Cambridge University Press:
- 11 April 2016, pp. 738-752
-
- Article
- Export citation
THE DUFFIN–SCHAEFFER-TYPE CONJECTURES IN VARIOUS LOCAL FIELDS
- Part of:
-
- Published online by Cambridge University Press:
- 06 May 2016, pp. 753-800
-
- Article
- Export citation
ON SIGN CHANGES FOR ALMOST PRIME COEFFICIENTS OF HALF-INTEGRAL WEIGHT MODULAR FORMS
- Part of:
-
- Published online by Cambridge University Press:
- 06 May 2016, pp. 801-810
-
- Article
- Export citation
A NOTE ON RANDOM MATRIX INTEGRALS, MOMENT IDENTITIES, AND CATALAN NUMBERS
- Part of:
-
- Published online by Cambridge University Press:
- 06 May 2016, pp. 811-817
-
- Article
- Export citation
MORE ON LOGARITHMIC SUMS OF CONVEX BODIES
- Part of:
-
- Published online by Cambridge University Press:
- 10 May 2016, pp. 818-841
-
- Article
- Export citation
ON BILINEAR EXPONENTIAL AND CHARACTER SUMS WITH RECIPROCALS OF POLYNOMIALS
- Part of:
-
- Published online by Cambridge University Press:
- 16 May 2016, pp. 842-859
-
- Article
- Export citation
SHORTEST DISTANCE IN MODULAR HYPERBOLA AND LEAST QUADRATIC NON-RESIDUE
- Part of:
-
- Published online by Cambridge University Press:
- 10 May 2016, pp. 860-865
-
- Article
- Export citation
SIGN OF FOURIER COEFFICIENTS OF MODULAR FORMS OF HALF-INTEGRAL WEIGHT
- Part of:
-
- Published online by Cambridge University Press:
- 17 May 2016, pp. 866-883
-
- Article
- Export citation
A DICHOTOMY LAW FOR THE DIOPHANTINE PROPERTIES IN
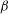 $\unicode[STIX]{x1D6FD}$ -DYNAMICAL SYSTEMS
$\unicode[STIX]{x1D6FD}$ -DYNAMICAL SYSTEMS
- Part of:
-
- Published online by Cambridge University Press:
- 16 May 2016, pp. 884-897
-
- Article
- Export citation
THE DIVISOR FUNCTION IN ARITHMETIC PROGRESSIONS MODULO PRIME POWERS
- Part of:
-
- Published online by Cambridge University Press:
- 17 May 2016, pp. 898-908
-
- Article
- Export citation
UPPER BOUND THEOREM FOR ODD-DIMENSIONAL FLAG TRIANGULATIONS OF MANIFOLDS
- Part of:
-
- Published online by Cambridge University Press:
- 01 June 2016, pp. 909-928
-
- Article
- Export citation
A LIMITING CASE OF ULTRASYMMETRIC SPACES
- Part of:
-
- Published online by Cambridge University Press:
- 01 June 2016, pp. 929-948
-
- Article
- Export citation
ON THE MONOTONICITY OF THE MOMENTS OF VOLUMES OF RANDOM SIMPLICES
- Part of:
-
- Published online by Cambridge University Press:
- 01 June 2016, pp. 949-958
-
- Article
- Export citation
Front Cover (OFC, IFC) and matter
MTK volume 62 Issue 3 Cover and Front matter
-
- Published online by Cambridge University Press:
- 13 September 2016, pp. f1-f2
-
- Article
-
- You have access
- Export citation
Back Cover (OBC, IBC) and matter
MTK volume 62 Issue 3 Cover and Back matter
-
- Published online by Cambridge University Press:
- 13 September 2016, pp. b1-b3
-
- Article
-
- You have access
- Export citation