Hostname: page-component-7dd5485656-wlg5v Total loading time: 0 Render date: 2025-10-31T08:34:14.314Z Has data issue: false hasContentIssue false
  • English
  • Français

A DICHOTOMY LAW FOR THE DIOPHANTINE PROPERTIES IN 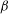$\unicode[STIX]{x1D6FD}$ -DYNAMICAL SYSTEMS

Part of: Diophantine approximation, transcendental number theory Probabilistic theory: distribution modulo $1$; metric theory of algorithms

Published online by Cambridge University Press:  16 May 2016

Michael Coons ,
Mumtaz Hussain  and
Bao-Wei Wang
Michael Coons
Affiliation:
School of Mathematical and Physical Sciences, University of Newcastle, Callaghan, NSW 2308, Australia email michael.coons@newcastle.edu.au
Mumtaz Hussain
Affiliation:
School of Mathematical and Physical Sciences, University of Newcastle, Callaghan, NSW 2308, Australia email mumtaz.hussain@newcastle.edu.au, drhussainmumtaz@gmail.com
Bao-Wei Wang
Affiliation:
School of Mathematics and Statistics, Huazhong University of Science and Technology, Wuhan 430074, China email bwei_wang@hust.edu.cn
Get access

Abstract

Let 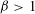$\unicode[STIX]{x1D6FD}>1$ be a real number and define the 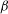$\unicode[STIX]{x1D6FD}$ -transformation on 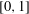$[0,1]$ by 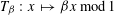$T_{\unicode[STIX]{x1D6FD}}:x\mapsto \unicode[STIX]{x1D6FD}x\,\text{mod}\,1$ . Further, define

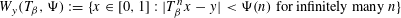$$\begin{eqnarray}W_{y}(T_{\unicode[STIX]{x1D6FD}},\unicode[STIX]{x1D6F9}):=\{x\in [0,1]:|T_{\unicode[STIX]{x1D6FD}}^{n}x-y|<\unicode[STIX]{x1D6F9}(n)\text{ for infinitely many }n\}\end{eqnarray}$$
and
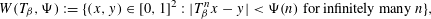$$\begin{eqnarray}W(T_{\unicode[STIX]{x1D6FD}},\unicode[STIX]{x1D6F9}):=\{(x,y)\in [0,1]^{2}:|T_{\unicode[STIX]{x1D6FD}}^{n}x-y|<\unicode[STIX]{x1D6F9}(n)\text{ for infinitely many }n\},\end{eqnarray}$$
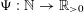 where $\unicode[STIX]{x1D6F9}:\mathbb{N}\rightarrow \mathbb{R}_{{>}0}$ is a positive function such that 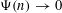$\unicode[STIX]{x1D6F9}(n)\rightarrow 0$ as 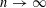$n\rightarrow \infty$ . In this paper, we show that each of the above sets obeys a Jarník-type dichotomy, that is, the generalized Hausdorff measure is either zero or full depending upon the convergence or divergence of a certain series. This work completes the metrical theory of these sets.

MSC classification

Primary: 11J83: Metric theory
Secondary: 11K60: Diophantine approximation 11K16: Normal numbers, radix expansions, Pisot numbers, Salem numbers, good lattice points, etc.

Information

Type
Research Article
Information
Mathematika , Volume 62 , Issue 3 , 2016 , pp. 884 - 897
Copyright
Copyright © University College London 2016 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Badziahin, D., Beresnevich, V. and Velani, S., Inhomogeneous theory of dual Diophantine approximation on manifolds. Adv. Math. 232 2013, 1–35; MR 2989975.CrossRefGoogle Scholar
Badziahin, D., Harrap, S. and Hussain, M., An inhomogeneous Jarník type theorem for planar curves. Preprint, 2015, arXiv:1503.04981.CrossRefGoogle Scholar
Baker, A. and Schmidt, W., Diophantine approximation and Hausdorff dimension. Proc. Lond. Math. Soc. (3) 21 1970, 1–11; MR 0271033 (42 #5916).CrossRefGoogle Scholar
Beresnevich, V., Dickinson, D. and Velani, S., Measure theoretic laws for lim sup sets. Mem. Amer. Math. Soc. 179(846) 2006; MR 2184760 (2007d:11086).Google Scholar
Beresnevich, V. and Velani, S., A mass transference principle and the Duffin–Schaeffer conjecture for Hausdorff measures. Ann. of Math. (2) 164(3) 2006, 971–992; MR 2259250 (2008a:11090).CrossRefGoogle Scholar
Beresnevich, V. and Velani, S., Schmidt’s theorem, Hausdorff measures, and slicing. Int. Math. Res. Not. IMRN 2006, 24, Art. ID 48794; MR 2264714 (2007h:11090).Google Scholar
Bernik, V. I. and Dodson, M. M., Metric Diophantine Approximation on Manifolds (Cambridge Tracts in Mathematics 137 ), Cambridge University Press (Cambridge, 1999); MR 1727177 (2001h:11091).CrossRefGoogle Scholar
Bugeaud, Y., On the 𝛽-expansion of an algebraic number in an algebraic base 𝛽. Integers 9(A20) 2009, 215–226; MR 2534910 (2010i:11101).CrossRefGoogle Scholar
Bugeaud, Y. and Wang, B., Distribution of full cylinders and the Diophantine properties of the orbits in 𝛽-expansions. J. Fractal Geom. 1(2) 2014, 221–241; MR 3230505.CrossRefGoogle Scholar
Chernov, N. and Kleinbock, D., Dynamical Borel–Cantelli lemmas for Gibbs measures. Israel J. Math. 122 2001, 1–27; MR 1826488 (2002h:37003).CrossRefGoogle Scholar
Dodson, M. M., A note on metric inhomogeneous Diophantine approximation. J. Aust. Math. Soc. Ser. A 62(2) 1997, 175–185; MR 1433207 (98b:11085).CrossRefGoogle Scholar
Dodson, M. M., Rynne, B. P. and Vickers, J. A. G., Diophantine approximation and a lower bound for Hausdorff dimension. Mathematika 37(1) 1990, 59–73; MR 1067887 (91i:11098).CrossRefGoogle Scholar
Falconer, K., Fractal Geometry, 2nd edn (Mathematical Foundations and Applications), John Wiley & Sons, Inc. (Hoboken, NJ, 2003); MR 2118797 (2006b:28001).CrossRefGoogle Scholar
Fan, A.-H. and Wang, B., On the lengths of basic intervals in beta expansions. Nonlinearity 25(5) 2012, 1329–1343; MR 2914142.CrossRefGoogle Scholar
Fuchs, M. and Kim, D., On Kurzweil’s 0-1 law in inhomogeneous diophantine approximation. Acta. Arith. 173 2016, 41–57, doi:10.4064/aa8219-1-2016.Google Scholar
Ge, Y. and Lü, F., A note on inhomogeneous Diophantine approximation in beta-dynamical system. Bull. Aust. Math. Soc. 91(1) 2015, 34–40; MR 3294256.CrossRefGoogle Scholar
Harman, G., Metric Number Theory (London Mathematical Society Monographs. New Series 18 ), The Clarendon Press, Oxford University Press (New York, 1998); MR 1672558 (99k:11112).CrossRefGoogle Scholar
Hill, R. and Velani, S., The ergodic theory of shrinking targets. Invent. Math. 119(1) 1995, 175–198; MR 1309976 (96e:58088).CrossRefGoogle Scholar
Hill, R. and Velani, S., The shrinking target problem for matrix transformations of tori. J. Lond. Math. Soc. (2) 60(2) 1999, 381–398; MR 1724857 (2000i:37003).CrossRefGoogle Scholar
Hill, R. and Velani, S., A zero-infinity law for well-approximable points in Julia sets. Ergodic Theory Dynam. Systems 22(6) 2002, 1773–1782; MR 1944403 (2003m:37065).CrossRefGoogle Scholar
Hofbauer, F., 𝛽-shifts have unique maximal measure. Monatsh. Math. 85(3) 1978, 189–198; MR 0492180 (58 #11326).CrossRefGoogle Scholar
Hussain, M. and Kristensen, S., Metrical results on systems of small linear forms. Int. J. Number Theory 9(3) 2013, 769–782; MR 3043613.CrossRefGoogle Scholar
Hussain, M. and Kristensen, S., Metrical theorems on systems of small inhomogeneous linear forms, Preprint, 2015, arXiv:1406.3930.Google Scholar
Hussain, M. and Levesley, J., The metrical theory of simultaneously small linear forms. Funct. Approx. Comment. Math. 48(2) 2013, 167–181; MR 3100138.CrossRefGoogle Scholar
Li, B., Wang, B., Wu, J. and Xu, J., The shrinking target problem in the dynamical system of continued fractions. Proc. Lond. Math. Soc. (3) 108(1) 2014, 159–186; MR 3162824.CrossRefGoogle Scholar
Parry, W., On the 𝛽-expansions of real numbers. Acta Math. Acad. Sci. Hungar. 11 1960, 401–416; MR 0142719 (26 #288).CrossRefGoogle Scholar
Persson, T. and Schmeling, J., Dyadic Diophantine approximation and Katok’s horseshoe approximation. Acta Arith. 132(3) 2008, 205–230; MR 2403650 (2009c:11111).CrossRefGoogle Scholar
Philipp, W., Some metrical theorems in number theory. Pacific J. Math. 20 1967, 109–127; MR 0205930 (34 #5755).CrossRefGoogle Scholar
Reeve, H., Shrinking targets for countable Markov maps. Preprint, 2011, arXiv:1107.4736.Google Scholar
Rényi, A., Representations for real numbers and their ergodic properties. Acta Math. Acad. Sci. Hungar 8 1957, 477–493; MR 0097374 (20 #3843).CrossRefGoogle Scholar
Schmeling, J., Symbolic dynamics for 𝛽-shifts and self-normal numbers. Ergodic Theory Dynam. Systems 17(3) 1997, 675–694; MR 1452189 (98c:11080).CrossRefGoogle Scholar
Shen, L. and Wang, B., Shrinking target problems for beta-dynamical system. Sci. China Math. 56(1) 2013, 91–104; MR 3016585.CrossRefGoogle Scholar
Tan, B. and Wang, B., Quantitative recurrence properties for beta-dynamical system. Adv. Math. 228(4) 2011, 2071–2097; MR 2836114.CrossRefGoogle Scholar
Tseng, J., On circle rotations and the shrinking target properties. Discrete Contin. Dyn. Syst. 20(4) 2008, 1111–1122; MR 2379490 (2010a:37080).CrossRefGoogle Scholar
Urbański, M., Diophantine analysis of conformal iterated function systems. Monatsh. Math. 137(4) 2002, 325–340; MR 1947918 (2004j:37085).CrossRefGoogle Scholar