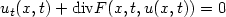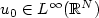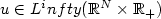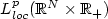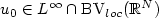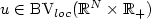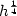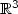Refine listing
Actions for selected content:
Contents
Research Article
On the stability of solutions of impulsive nonlinear parabolic equations
-
- Published online by Cambridge University Press:
- 15 August 2002, pp. 351-357
-
- Article
- Export citation
3D domain decomposition method coupling conforming and nonconforming finite elements
-
- Published online by Cambridge University Press:
- 15 August 2002, pp. 771-780
-
- Article
- Export citation
Analysis of a one-dimensional variational modelofthe equilibrium shapel of a deformable crystal
-
- Published online by Cambridge University Press:
- 15 August 2002, pp. 573-591
-
- Article
- Export citation
An adaptive finite element method for solving a double well problem describing crystalline microstructure
-
- Published online by Cambridge University Press:
- 15 August 2002, pp. 781-796
-
- Article
- Export citation
A multidimensional fluctuation splitting schemeforthe three dimensional Euler equations
-
- Published online by Cambridge University Press:
- 15 August 2002, pp. 1241-1259
-
- Article
- Export citation
Sur un problème parabolique-elliptique
-
- Published online by Cambridge University Press:
- 15 August 2002, pp. 121-127
-
- Article
- Export citation
On the linear force-free fields in bounded andunbounded three-dimensional domains
-
- Published online by Cambridge University Press:
- 15 August 2002, pp. 359-393
-
- Article
- Export citation
A numerical method for solving inverse eigenvalue problems
-
- Published online by Cambridge University Press:
- 15 August 2002, pp. 1003-1017
-
- Article
- Export citation
Finite volume schemes for a nonlinear hyperbolic equation. Convergence towards the entropy solution and error estimate
-
- Published online by Cambridge University Press:
- 15 August 2002, pp. 129-156
-
- Article
- Export citation
Existence of a solution for a nonlinearly elastic plane membrane “under tension”
-
- Published online by Cambridge University Press:
- 15 August 2002, pp. 1019-1032
-
- Article
- Export citation
A strongly nonlinear problem arising in glaciology
-
- Published online by Cambridge University Press:
- 15 August 2002, pp. 395-406
-
- Article
- Export citation
Mathematical and numerical studies ofnon linear ferromagnetic materials
-
- Published online by Cambridge University Press:
- 15 August 2002, pp. 593-626
-
- Article
- Export citation
Motion of spirals by crystalline curvature
-
- Published online by Cambridge University Press:
- 15 August 2002, pp. 797-806
-
- Article
- Export citation
A class of time discrete schemes for a phase–field systemof Penrose–Fife type
-
- Published online by Cambridge University Press:
- 15 August 2002, pp. 1261-1292
-
- Article
- Export citation
On the combined effect of boundary approximationand numerical integration on mixed finite element solutionof 4th order elliptic problems with variable coefficients
-
- Published online by Cambridge University Press:
- 15 August 2002, pp. 807-836
-
- Article
- Export citation
Stabilization of Galerkin approximations of transport equations by subgrid modeling
-
- Published online by Cambridge University Press:
- 15 August 2002, pp. 1293-1316
-
- Article
- Export citation
Singularities of Maxwell interface problems
-
- Published online by Cambridge University Press:
- 15 August 2002, pp. 627-649
-
- Article
- Export citation
Coupling the Stokes and Navier–Stokes equations with two scalarnonlinear parabolic equations
-
- Published online by Cambridge University Press:
- 15 August 2002, pp. 157-167
-
- Article
- Export citation
Convergence of a finite element discretizationof the Navier-Stokes equationsin vorticity and stream function formulation
-
- Published online by Cambridge University Press:
- 15 August 2002, pp. 1033-1056
-
- Article
- Export citation
Boundary observability for the space semi-discretizationsof the 1 – d wave equation
-
- Published online by Cambridge University Press:
- 15 August 2002, pp. 407-438
-
- Article
- Export citation