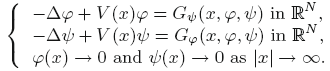Refine listing
Actions for selected content:
Contents
Research Article
Unique continuation principle for systemsof parabolic equations
-
- Published online by Cambridge University Press:
- 10 February 2009, pp. 247-274
-
- Article
- Export citation
Evolutionary problems in non-reflexive spaces
-
- Published online by Cambridge University Press:
- 21 October 2008, pp. 1-22
-
- Article
- Export citation
Evolution equations in discrete and continuous time for nonexpansive operators in Banach spaces
-
- Published online by Cambridge University Press:
- 31 July 2009, pp. 809-832
-
- Article
- Export citation
A sensitivity-based extrapolation techniquefor the numerical solution of state-constrained optimal control problems
-
- Published online by Cambridge University Press:
- 02 July 2009, pp. 503-522
-
- Article
- Export citation
Homogenization of variational problemsin manifold valued Sobolev spaces
-
- Published online by Cambridge University Press:
- 31 July 2009, pp. 833-855
-
- Article
- Export citation
Uniqueness of stable Meissner state solutionsof the Chern-Simons-Higgs energy
-
- Published online by Cambridge University Press:
- 21 October 2008, pp. 23-36
-
- Article
- Export citation
A penalty method for topology optimization subject to a pointwise state constraint
-
- Published online by Cambridge University Press:
- 18 June 2009, pp. 523-544
-
- Article
- Export citation
Projective Reeds-Shepp car on S 2 with quadratic cost
-
- Published online by Cambridge University Press:
- 19 December 2008, pp. 275-297
-
- Article
- Export citation
Upper bounds for a class of energies containinga non-local term
-
- Published online by Cambridge University Press:
- 31 July 2009, pp. 856-886
-
- Article
- Export citation
Observability properties of a semi-discrete 1d wave equation derived from a mixed finite element methodon nonuniform meshes
-
- Published online by Cambridge University Press:
- 19 December 2008, pp. 298-326
-
- Article
- Export citation
Magnetic vortices for a Ginzburg-Landau type energywithdiscontinuous constraint
-
- Published online by Cambridge University Press:
- 18 June 2009, pp. 545-580
-
- Article
- Export citation
On the integral representation of relaxed functionalswith convex bounded constraints
-
- Published online by Cambridge University Press:
- 21 October 2008, pp. 37-57
-
- Article
- Export citation
Uniqueness of solutions for some elliptic equations with a quadratic gradient term
-
- Published online by Cambridge University Press:
- 19 December 2008, pp. 327-336
-
- Article
- Export citation
Recent advances in the analysis of pointwise state-constrainedelliptic optimal control problems
-
- Published online by Cambridge University Press:
- 02 July 2009, pp. 581-600
-
- Article
- Export citation
Homogenization of monotone systemsof Hamilton-Jacobi equations
-
- Published online by Cambridge University Press:
- 21 October 2008, pp. 58-76
-
- Article
- Export citation
Necessary and sufficient Lyapunov-like conditions for robust nonlinear stabilization
-
- Published online by Cambridge University Press:
- 11 August 2009, pp. 887-928
-
- Article
- Export citation
Semicontinuity theorem in the micropolar elasticity
-
- Published online by Cambridge University Press:
- 10 February 2009, pp. 337-355
-
- Article
- Export citation
Nonlinear feedback stabilizationof a two-dimensional Burgers equation
-
- Published online by Cambridge University Press:
- 31 July 2009, pp. 929-955
-
- Article
- Export citation
Infinitely many solutions for asymptotically linear periodicHamiltonian elliptic systems
-
- Published online by Cambridge University Press:
- 21 October 2008, pp. 77-91
-
- Article
- Export citation
Metric subregularity for nonclosed convex multifunctions innormed spaces
-
- Published online by Cambridge University Press:
- 18 June 2009, pp. 601-617
-
- Article
- Export citation