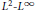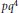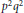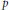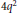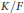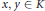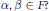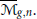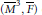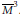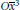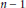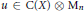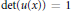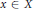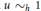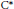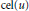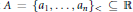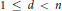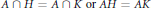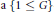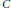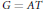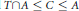Contents
Research Article
Complexifying Lie Group Actions on Homogeneous Manifolds of Non-compact Dimension Two
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 673-682
-
- Article
-
- You have access
- Export citation
Topological Games and Alster Spaces
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 683-696
-
- Article
-
- You have access
- Export citation
On the Monodromy of Milnor Fibers of Hyperplane Arrangements
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 697-707
-
- Article
-
- You have access
- Export citation
Strong Asymptotic Freeness for Free Orthogonal Quantum Groups
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 708-720
-
- Article
-
- You have access
- Export citation
Classification of Integral Modular Categories of Frobenius–Perron Dimension pq 4 and p 2 q 2
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 721-734
-
- Article
-
- You have access
- Export citation
On the Theorem of the Primitive Element with Applications to the Representation Theory of Associative and Lie Algebras
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 735-748
-
- Article
-
- You have access
- Export citation
Geometric Perspective on Piecewise Polynomiality of Double Hurwitz Numbers
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 749-764
-
- Article
-
- You have access
- Export citation
Helicoidal Minimal Surfaces in a Finsler Space of Randers Type
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 765-779
-
- Article
-
- You have access
- Export citation
Measures of Noncompactness in Regular Spaces
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 780-793
-
- Article
-
- You have access
- Export citation
New Characterizations of the Weighted Composition Operators Between Bloch Type Spaces in the Polydisk
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 794-802
-
- Article
-
- You have access
- Export citation
Free Locally Convex Spaces and the k-space Property
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 803-809
-
- Article
-
- You have access
- Export citation
Uniqueness of Preduals in Spaces of Operators
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 810-813
-
- Article
-
- You have access
- Export citation
On Global Dimensions of Tree Type Finite Dimensional Algebras
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 814-820
-
- Article
-
- You have access
- Export citation
Real Hypersurfaces in Complex Two-Plane Grassmannians with Reeb Parallel Structure Jacobi Operator
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 821-833
-
- Article
-
- You have access
- Export citation
Restriction Operators Acting on Radial Functions on Vector Spaces over Finite Fields
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 834-844
-
- Article
-
- You have access
- Export citation
Factorisation of Two-variable p-adic L-functions
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 845-852
-
- Article
-
- You have access
- Export citation
On the Bound of the C* Exponential Length
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 853-869
-
- Article
-
- You have access
- Export citation
A Short Note on Short Pants
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 870-876
-
- Article
-
- You have access
- Export citation
On Convolutions of Convex Sets and Related Problems
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 877-883
-
- Article
-
- You have access
- Export citation
m-embedded Subgroups and p-nilpotency of Finite Groups
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 884-889
-
- Article
-
- You have access
- Export citation