Hostname: page-component-7dd5485656-tbj44 Total loading time: 0 Render date: 2025-10-30T22:53:34.517Z Has data issue: false hasContentIssue false
  • English
  • Français

Strong Asymptotic Freeness for Free Orthogonal Quantum Groups

Published online by Cambridge University Press:  20 November 2018

Michael Brannan
Michael Brannan*
Affiliation:
Department of Mathematics, University of Illinois at Urbana-Champaign, Urbana, IL 61801, USA e-mail: mbrannan@illinois.edu
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

It is known that the normalized standard generators of the free orthogonal quantum group 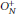$O_{N}^{+}$ converge in distribution to a free semicircular system as 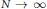$N\,\to \,\infty$ . In this note, we substantially improve this convergence result by proving that, in addition to distributional convergence, the operator normof any non-commutative polynomial in the normalized standard generators of 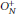$O_{N}^{+}$ converges as 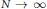$N\,\to \,\infty$ to the operator norm of the corresponding non-commutative polynomial in a standard free semicircular system. Analogous strong convergence results are obtained for the generators of free unitary quantum groups. As applications of these results, we obtain a matrix-coefficient version of our strong convergence theorem, and we recover a well-known 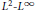${{\mathcal{L}}^{2}}\,-\,{{\mathcal{L}}^{\infty }}$ norm equivalence for noncommutative polynomials in free semicircular systems.

Keywords

46L5420G4246L65quantum groupsfree probabilityasymptotic free independencestrong convergenceproperty of rapid decay

Information

Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 57 , Issue 4 , 01 December 2014 , pp. 708 - 720
Copyright
Copyright © Canadian Mathematical Society 2014

References

[1] Aubert, S. and Lam, C. S., Invariant integration over the unitary group. J. Math. Phys. 44 (2003), 6112–6131. http://dx.doi.org/10.1063/1.1622448 Google Scholar
[2] Banica, T., Théorie des représentations du groupe quantique compact libre O(n). C. R. Acad. Sci. Paris Sér. I Math. 322 (1996), 241–244.Google Scholar
[3] Banica, T., Le groupe quantique compact libre U(n). Comm. Math. Phys. 190 (1997), 143–172. http://dx.doi.org/10.1007/s002200050237 Google Scholar
[4] Banica, T. and Collins, B., Integration over compact quantum groups.Publ. Res. Inst. Math. Sci. 43 (2007), 277–302. http://dx.doi.org/10.2977/prims/1201011782 Google Scholar
[5] Banica, T. and Collins, B., Integration over quantum permutation groups. J. Funct. Anal. 242 (2007), 641–657. http://dx.doi.org/10.1016/j.jfa.2006.09.005 Google Scholar
[6] Banica, T., B. Collins and P. Zinn-Justin, Spectral analysis of the free orthogonal matrix.Int. Math. Res. Notices 17 (2009), 3286–3309.Google Scholar
[7] Banica, T., S. Curran and Speicher, R., De Finetti theorems for easy quantum groups. Ann. Probab. 40 (2012), 401–435. http://dx.doi.org/10.1214/10-AOP619 Google Scholar
[8] Banica, T. and Speicher, R., Liberation of orthogonal Lie groups. Adv. Math. 222 (2009), 1461–1501. http://dx.doi.org/10.1016/j.aim.2009.06.009 Google Scholar
[9] Bercovici, H. and Voiculescu, D., Superconvergence to the central limit and failure of the Cramér theorem for free random variables. Probab. Theory Related Fields 103 (1995), 215–222. http://dx.doi.org/10.1007/BF01204215 Google Scholar
[10] Biane, P. and Speicher, R., Stochastic calculus with respect to free Brownian motion and analysis on Wigner space.Probab. Theory Related Fields 112 (1998), 373–409. http://dx.doi.org/10.1007/s004400050194 Google Scholar
[11] Bozejko, M., A q-deformed probability, Nelson's inequality and central limit theorems. In: Nonlinear fields, classical, random, semiclassical (P. Garbecaki and Popowci, Z., eds.), World Scientific, Singapore, 1991, 312–335.Google Scholar
[12] Brannan, M., Reduced operator algebras of trace-preserving quantum automorphism groups. Preprint, 2012. arxiv:1202.5020.Google Scholar
[13] Brannan, M., Approximation properties for free orthogonal and free unitary quantum groups. J. Reine Angew. Math. 672 (2012), 223–251.Google Scholar
[14] Collins, B., Moments and Cumulants of Polynomial random variables on unitary groups, the Itzykson–Zuber integral and free probability. Int. Math. Res. Not. 17 (2003), 953–982.Google Scholar
[15] Collins, B. and Male, C., The strong asymptotic freeness of Haar and deterministic matrices. Ann. Sci. de l’ENS (2013), to appear.Google Scholar
[16] Collins, B. and Piotr Sniady, Integration with respect to the Haar measure on unitary, orthogonal and symplectic group. Comm. Math. Phys. 264 (2006), 773–795. http://dx.doi.org/10.1007/s00220-006-1554-3 Google Scholar
[17] Diaconis, P. and Freedman, D., A dozen de Finetti-style results in search of a theory. Ann. Inst. H. Poincaré Probab. Statist. 23 (1987), 397–423.Google Scholar
[18] Freslon, A., Examples of weakly amenable discrete quantum groups.J. Funct. Anal. 265 (2013), 2164–2187. http://dx.doi.org/10.1016/j.jfa.2013.05.037 Google Scholar
[19] Haagerup, U., An example of a nonnuclear C*-algebra, which has the metric approximation property.Invent. Math. 50(1978/79), 279–293. http://dx.doi.org/10.1007/BF01410082 Google Scholar
[20] Haagerup, U. and Thorbjornson, S., A new application of random matrices: Ext C* red(F2)is not a group. Ann. Math. 162 (2005), 711–775. http://dx.doi.org/10.4007/annals.2005.162.711 Google Scholar
[21] Isono, Y., Examples of factors which have no Cartan subalgebras. Preprint, 2012. arxiv:1209.1728.Google Scholar
[22] Kallenberg, O., Probabilistic symmetries and invariance principles. Probability Appl., Springer-Verlag, New York, 2005.Google Scholar
[23] Kauffman, L. and Lins, S., Temperley–Lieb recoupling theory and invariants of 3-manifolds.Ann. Math. Stud. 134, Princeton University Press, 1994.Google Scholar
[24] Male, C., The norm of polynomials in large random and deterministic matrices.Probab. Theory Related Fields 154 (2012), 477–532. http://dx.doi.org/10.1007/s00440-011-0375-2 Google Scholar
[25] Matsumoto, S. and Novak, J., Jucys–Murphy elements and unitary matrix integrals. Int. Math. Res. Not. 2 (2013), 362–397.Google Scholar
[26] Nica, A. and Speicher, R., Lectures on the combinatorics of free probability.London Math. Soc. Lect. Note Ser. 335, Cambridge University Press, Cambridge, 2006.Google Scholar
[27] Pisier, G., Remarks on a recent result by Paul Skoufranis. Preprint, 2012. arxiv:1203.3186.Google Scholar
[28] Skoufranis, P., On a notion of exactness for reduced free products of C*-algebras. J. Reine Angew. Math., to appear.Google Scholar
[29] Timmerman, T., An invitation to quantum groups and duality. EMS Textbooks in Mathematics, Zurich, 2008.Google Scholar
[30] Vaes, S. and Vergnioux, R., The boundary of universal discrete quantum groups, exactness, and factoriality.Duke Math. J. 140 (2007), 35–84. http://dx.doi.org/10.1215/S0012-7094-07-14012-2 Google Scholar
[31] Vergnioux, R., The property of rapid decay for discrete quantum groups.J. Operator Theory 57 (2007), 303–324.Google Scholar
[32] Wang, S., Free products of compact quantum groups. Comm. Math. Phys. 167 (1995), 671–692. http://dx.doi.org/10.1007/BF02101540 Google Scholar
[33] Wang, S., Quantum symmetry groups of finite spaces.Comm. Math. Phys. 195 (1998), 195–211. http://dx.doi.org/10.1007/s002200050385 Google Scholar
[34] Woronowicz, S., Compact matrix pseudogroups. Comm. Math. Phys. 111 (1987), 613–665. http://dx.doi.org/10.1007/BF01219077 Google Scholar
[35] Woronowicz, S., Compact quantum groups. In: Symétries quantiques (Les Houches, 1995), North-Holland, Amsterdam, 1998, 845–884.Google Scholar