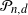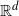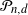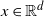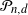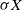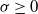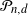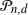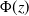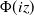1. Statement of main results
1.1. Introduction
Let ![]() $X_1,\ldots,X_n$
be independent random vectors with standard Gaussian distribution on
$X_1,\ldots,X_n$
be independent random vectors with standard Gaussian distribution on ![]() $\mathbb{R}^d$
. The Gaussian polytope
$\mathbb{R}^d$
. The Gaussian polytope ![]() $\mathcal{P}_{n,d}$
is defined as the convex hull of
$\mathcal{P}_{n,d}$
is defined as the convex hull of ![]() $X_1,\ldots,X_n$
, that is,
$X_1,\ldots,X_n$
, that is,
 \begin{equation*}\mathcal{P}_{n,d}=\mathop{\mathrm{conv}}\nolimits\!(X_1,\ldots,X_n) =\left\{\sum_{i=1}^n \lambda_i X_i \colon \lambda_1,\ldots,\lambda_n \geq 0, \sum_{i=1}^n \lambda_i = 1\right\}.\end{equation*}
\begin{equation*}\mathcal{P}_{n,d}=\mathop{\mathrm{conv}}\nolimits\!(X_1,\ldots,X_n) =\left\{\sum_{i=1}^n \lambda_i X_i \colon \lambda_1,\ldots,\lambda_n \geq 0, \sum_{i=1}^n \lambda_i = 1\right\}.\end{equation*}
The main aim of the present paper is to provide an explicit expression for the absorption probability, that is, the probability that ![]() $\mathcal{P}_{n,d}$
contains a given deterministic point
$\mathcal{P}_{n,d}$
contains a given deterministic point ![]() $x\in\mathbb{R}^d$
. By rotational symmetry, the absorption probability depends only on the Euclidean norm
$x\in\mathbb{R}^d$
. By rotational symmetry, the absorption probability depends only on the Euclidean norm ![]() $|x|$
. It turns out that it is more convenient to pass to the complementary event and consider the non-absorption probability
$|x|$
. It turns out that it is more convenient to pass to the complementary event and consider the non-absorption probability
A classical result of Wendel [Reference Wendel31] (which is valid in a setting more general than the Gaussian one considered here; see also [Reference Schneider and Weil28, Theorem 8.2.1]), states that
We shall compute ![]() $f_{n,d}(r)$
for general
$f_{n,d}(r)$
for general ![]() $r\geq 0$
. The main idea is that we shall make the point x random, with a rotationally symmetric Gaussian distribution and a certain variance
$r\geq 0$
. The main idea is that we shall make the point x random, with a rotationally symmetric Gaussian distribution and a certain variance ![]() $\sigma^2\geq 0$
. Namely, let X be a d-dimensional standard Gaussian random vector which is independent of
$\sigma^2\geq 0$
. Namely, let X be a d-dimensional standard Gaussian random vector which is independent of ![]() $X_1,\ldots,X_n$
. We shall compute
$X_1,\ldots,X_n$
. We shall compute
This probability can be related to a certain Laplace-type transform of ![]() $f_{n,d}$
. After inverting the Laplace transform, we shall obtain a formula for
$f_{n,d}$
. After inverting the Laplace transform, we shall obtain a formula for ![]() $f_{n,d}$
. This formula involves a certain function
$f_{n,d}$
. This formula involves a certain function ![]() $g_n(r)$
which expresses the volume of regular spherical simplices and which will be studied in detail below.
$g_n(r)$
which expresses the volume of regular spherical simplices and which will be studied in detail below.
The probability ![]() $p_{n,d}(\sigma^2)$
is closely related to the expected number of faces of the polytope
$p_{n,d}(\sigma^2)$
is closely related to the expected number of faces of the polytope ![]() $\mathcal{P}_{n,d}$
. Let
$\mathcal{P}_{n,d}$
. Let ![]() $f_k(\mathcal{P}_{n,d})$
be the number of k-dimensional faces (k-faces) of
$f_k(\mathcal{P}_{n,d})$
be the number of k-dimensional faces (k-faces) of ![]() $\mathcal{P}_{n,d}$
. Exact formulas for
$\mathcal{P}_{n,d}$
. Exact formulas for ![]() $\mathbb E f_{k}(\mathcal{P}_{n,d})$
were derived by Rényi and Sulanke [22, Section 4] (for
$\mathbb E f_{k}(\mathcal{P}_{n,d})$
were derived by Rényi and Sulanke [22, Section 4] (for ![]() $d=2$
), Efron [Reference Efron13] (for
$d=2$
), Efron [Reference Efron13] (for ![]() $d=2,3$
), Raynaud [Reference Raynaud21] (for faces of maximal dimension, that is, for
$d=2,3$
), Raynaud [Reference Raynaud21] (for faces of maximal dimension, that is, for ![]() $k=d-1$
). Affentranger [Reference Affentranger2] proved an asymptotic formula valid for general d and k; see also Carnal [Reference Carnal10] for the case
$k=d-1$
). Affentranger [Reference Affentranger2] proved an asymptotic formula valid for general d and k; see also Carnal [Reference Carnal10] for the case ![]() $d=2$
. Baryshnikov and Vitale [Reference Baryshnikov and Vitale5] showed that the expected number of k-faces of
$d=2$
. Baryshnikov and Vitale [Reference Baryshnikov and Vitale5] showed that the expected number of k-faces of ![]() $\mathcal{P}_{n,d}$
is the same as the expected number of k-faces of a random projection of the regular simplex with n vertices onto a uniformly chosen linear subspace of dimension d (the so-called Goodman–Pollack model). Finally, Affentranger and Schneider [Reference Affentranger and Schneider3] expressed the expected number of k-faces of the random projection of any polytope in terms of the internal and external angles of that polytope. Combining the results of Affentranger and Schneider [Reference Affentranger and Schneider3] and Baryshnikov and Vitale [Reference Baryshnikov and Vitale5], one obtains an expression for
$\mathcal{P}_{n,d}$
is the same as the expected number of k-faces of a random projection of the regular simplex with n vertices onto a uniformly chosen linear subspace of dimension d (the so-called Goodman–Pollack model). Finally, Affentranger and Schneider [Reference Affentranger and Schneider3] expressed the expected number of k-faces of the random projection of any polytope in terms of the internal and external angles of that polytope. Combining the results of Affentranger and Schneider [Reference Affentranger and Schneider3] and Baryshnikov and Vitale [Reference Baryshnikov and Vitale5], one obtains an expression for ![]() $\mathbb E f_k(\mathcal{P}_{n,d})$
in terms of the internal and external angles of the regular simplex.
$\mathbb E f_k(\mathcal{P}_{n,d})$
in terms of the internal and external angles of the regular simplex.
Hug et al. [Reference Hug, Munsonius and Reitzner16] expressed some important functionals of the Gaussian polytope, including the expected number of k-faces, through probabilities of the form ![]() $p_{n,d}(\sigma^2)$
and computed their asymptotics. As a by-product of our results, we shall provide explicit formulas for these functionals, thus recovering the results obtained in [Reference Affentranger and Schneider3] and [Reference Hug, Munsonius and Reitzner16]. Recent surveys on random polytopes can be found in [Reference Hug15], [Reference Majumdar, Comtet and Randon-Furling20], and [Reference Schneider27].
$p_{n,d}(\sigma^2)$
and computed their asymptotics. As a by-product of our results, we shall provide explicit formulas for these functionals, thus recovering the results obtained in [Reference Affentranger and Schneider3] and [Reference Hug, Munsonius and Reitzner16]. Recent surveys on random polytopes can be found in [Reference Hug15], [Reference Majumdar, Comtet and Randon-Furling20], and [Reference Schneider27].
1.2. Non-absorption probabilities
Our explicit formulas will be stated in terms of the functions ![]() $g_n(r)$
,
$g_n(r)$
, ![]() $n\in\mathbb{N}_0$
, defined by
$n\in\mathbb{N}_0$
, defined by ![]() $g_0(r)\coloneqq 1$
and
$g_0(r)\coloneqq 1$
and
where ![]() $(\eta_1,\ldots,\eta_n)$
is a zero-mean Gaussian vector with
$(\eta_1,\ldots,\eta_n)$
is a zero-mean Gaussian vector with
 \begin{equation}\mathop{\mathrm{Cov}}\nolimits (\eta_i,\eta_j)=\begin{cases}1+r, &\text{ if } i=j,\\[5pt]
r, &\text{ if } i\neq j.\end{cases}\end{equation}
\begin{equation}\mathop{\mathrm{Cov}}\nolimits (\eta_i,\eta_j)=\begin{cases}1+r, &\text{ if } i=j,\\[5pt]
r, &\text{ if } i\neq j.\end{cases}\end{equation}
The fact that (1.5) indeed defines a valid (i.e., positive semidefinite) covariance matrix for ![]() $r\geq -1/n$
is easily verified using the inequality between the arithmetic and quadratic means.
$r\geq -1/n$
is easily verified using the inequality between the arithmetic and quadratic means.
Many known and some new properties of the function ![]() $g_n$
(which is closely related to the Schläfli function [Reference Böhm and Hertel8]) will be collected in Sections 1.3 and 1.4. At this point, we just state an explicit expression for
$g_n$
(which is closely related to the Schläfli function [Reference Böhm and Hertel8]) will be collected in Sections 1.3 and 1.4. At this point, we just state an explicit expression for ![]() $g_n$
in terms of the standard normal distribution function
$g_n$
in terms of the standard normal distribution function ![]() $\Phi$
. It is known that
$\Phi$
. It is known that ![]() $\Phi$
admits an analytic continuation to the entire complex plane. We shall need its values on the real and imaginary axes, namely
$\Phi$
admits an analytic continuation to the entire complex plane. We shall need its values on the real and imaginary axes, namely
The reader more used to the error function ![]() $\operatorname{erf}$
may transform everything by applying the formula
$\operatorname{erf}$
may transform everything by applying the formula ![]() $\Phi(z) = 1/2 + \operatorname{erf}(z/\sqrt 2)$
. With this notation, an explicit formula for
$\Phi(z) = 1/2 + \operatorname{erf}(z/\sqrt 2)$
. With this notation, an explicit formula for ![]() $g_n$
reads as follows:
$g_n$
reads as follows:
 \begin{align}&=\begin{cases}\frac {1}{\sqrt{2\pi}} \int_{-\infty}^{\infty} \left(\frac{1}{\sqrt{2\pi}} \int_{-\infty}^{x\sqrt r} {\rm e}^{-z^2/2} {\rm d} z\right)^{n}{\rm e}^{-x^2/2}{\rm d} x, &\text{if } r\geq 0,\\[12pt]
\frac {2}{\sqrt{\pi}} \int_0^{\infty} \operatorname{Re} \left[\left(\frac 12 + \frac{i}{\sqrt{\pi}} \int_0^{x\sqrt{-r}} {\rm e}^{z^2} {\rm d} z\right)^{n}\right]{\rm e}^{-x^2}{\rm d} x, &\text{if } -1/n\leq r \leq 0,\end{cases}\end{align}
\begin{align}&=\begin{cases}\frac {1}{\sqrt{2\pi}} \int_{-\infty}^{\infty} \left(\frac{1}{\sqrt{2\pi}} \int_{-\infty}^{x\sqrt r} {\rm e}^{-z^2/2} {\rm d} z\right)^{n}{\rm e}^{-x^2/2}{\rm d} x, &\text{if } r\geq 0,\\[12pt]
\frac {2}{\sqrt{\pi}} \int_0^{\infty} \operatorname{Re} \left[\left(\frac 12 + \frac{i}{\sqrt{\pi}} \int_0^{x\sqrt{-r}} {\rm e}^{z^2} {\rm d} z\right)^{n}\right]{\rm e}^{-x^2}{\rm d} x, &\text{if } -1/n\leq r \leq 0,\end{cases}\end{align}
where in (1.7) we agree that ![]() $\sqrt{r} = i\sqrt{-r}$
if
$\sqrt{r} = i\sqrt{-r}$
if ![]() $r<0$
. The next theorem provides a formula for the probability that
$r<0$
. The next theorem provides a formula for the probability that ![]() $\sigma X \notin \mathcal{P}_{n,d}$
.
$\sigma X \notin \mathcal{P}_{n,d}$
.
Theorem 1.1. Let ![]() $X,X_1,\ldots,X_n$
be independent standard Gaussian random vectors in
$X,X_1,\ldots,X_n$
be independent standard Gaussian random vectors in ![]() $\mathbb{R}^d$
, where
$\mathbb{R}^d$
, where ![]() $n\geq d+1$
. Then, for every
$n\geq d+1$
. Then, for every ![]() $\sigma\geq 0$
,
$\sigma\geq 0$
,
where
for ![]() $k=0,\ldots,n$
, and
$k=0,\ldots,n$
, and ![]() $b_{n,k}=0$
for
$b_{n,k}=0$
for ![]() $k\notin \{0,1,\ldots,n\}$
.
$k\notin \{0,1,\ldots,n\}$
.
The proof of Theorem 1.1 will be given in Section 2. The main idea is to interpret ![]() $p_{n,d}(\sigma^2)$
as the probability that a uniform random linear subspace intersects a certain n-dimensional convex cone
$p_{n,d}(\sigma^2)$
as the probability that a uniform random linear subspace intersects a certain n-dimensional convex cone ![]() $C= C_n(\sigma^2)$
. By the conic Crofton formula (which will be recalled in Theorem 2.1 below), this intersection probability can be expressed in terms of the conic intrinsic volumes
$C= C_n(\sigma^2)$
. By the conic Crofton formula (which will be recalled in Theorem 2.1 below), this intersection probability can be expressed in terms of the conic intrinsic volumes ![]() $\upsilon_0(C),\ldots, \upsilon_n(C)$
of C. At this point, we can forget about the original problem and concentrate on computing the conic intrinsic volumes, which is a purely geometric problem. It turns out that
$\upsilon_0(C),\ldots, \upsilon_n(C)$
of C. At this point, we can forget about the original problem and concentrate on computing the conic intrinsic volumes, which is a purely geometric problem. It turns out that ![]() $\upsilon_k(C) = b_{n,k}(\sigma^2)$
; see Proposition 1.3 below.
$\upsilon_k(C) = b_{n,k}(\sigma^2)$
; see Proposition 1.3 below.
Example 1.1. (Wendel’s formula.) Let ![]() $\sigma^2 = 0$
. By symmetry reasons it is clear (and will be stated in Proposition 1.4 (d)) that
$\sigma^2 = 0$
. By symmetry reasons it is clear (and will be stated in Proposition 1.4 (d)) that ![]() $g_k(0) = 2^{-k}$
,
$g_k(0) = 2^{-k}$
, ![]() $g_{n-k}(0) = 2^{-(n-k)}$
, and hence
$g_{n-k}(0) = 2^{-(n-k)}$
, and hence ![]() $b_{n,k}(0) = 2^{-n} \binom nk$
. Theorem 1.1 simplifies to
$b_{n,k}(0) = 2^{-n} \binom nk$
. Theorem 1.1 simplifies to
 \begin{align}\mathbb{P}[0\notin \mathop{\mathrm{conv}}\nolimits (X_1,\ldots,X_n)]&=\frac1{2^{n-1}} \left(\binom{n}{d-1} + \binom{n}{d-3} +\ldots \right)\\
&=\frac1{2^{n-1}} \left(\binom{n-1}{d-1} + \binom{n-1}{d-2} +\ldots \right) \notag,\end{align}
\begin{align}\mathbb{P}[0\notin \mathop{\mathrm{conv}}\nolimits (X_1,\ldots,X_n)]&=\frac1{2^{n-1}} \left(\binom{n}{d-1} + \binom{n}{d-3} +\ldots \right)\\
&=\frac1{2^{n-1}} \left(\binom{n-1}{d-1} + \binom{n-1}{d-2} +\ldots \right) \notag,\end{align}
where in the second line we used the defining property of the Pascal triangle. This recovers Wendel’s formula (1.2) in the Gaussian case.
By conditioning on X in Theorem 1.1, we shall derive the following result.
Corollary 1.1. The function ![]() $f_{n,d}(|x|) = \mathbb{P}[x \notin \mathop{\mathrm{conv}}\nolimits(X_1,\ldots,X_n)]$
satisfies
$f_{n,d}(|x|) = \mathbb{P}[x \notin \mathop{\mathrm{conv}}\nolimits(X_1,\ldots,X_n)]$
satisfies
for all ![]() $\lambda>0$
.
$\lambda>0$
.
It is possible to invert the Laplace transform explicitly. Recall that ![]() $\Phi$
is the standard normal distribution function.
$\Phi$
is the standard normal distribution function.
Theorem 1.2. For all ![]() $u> 0$
we have
$u> 0$
we have
where ![]() $f_{n,d}(0)$
is given by Wendel’s formula (1.2) and
$f_{n,d}(0)$
is given by Wendel’s formula (1.2) and
 \begin{align}F_{k,n-k} (v) &=\frac 1 {\pi}\int_0^v\left(\frac{\Phi^{n-k}(\sqrt{2 w}) + \Phi^{n-k}({-}\sqrt{2 w})}{2\sqrt w} \right.\notag\\[5pt]
&\qquad \qquad\cdot\left.\frac{\Phi^{k} (i \sqrt{2(v-w)}) + \Phi^{k} ({-}i \sqrt{2(v-w)})}{2\sqrt{v-w}}\right){\rm d} w. \end{align}
\begin{align}F_{k,n-k} (v) &=\frac 1 {\pi}\int_0^v\left(\frac{\Phi^{n-k}(\sqrt{2 w}) + \Phi^{n-k}({-}\sqrt{2 w})}{2\sqrt w} \right.\notag\\[5pt]
&\qquad \qquad\cdot\left.\frac{\Phi^{k} (i \sqrt{2(v-w)}) + \Phi^{k} ({-}i \sqrt{2(v-w)})}{2\sqrt{v-w}}\right){\rm d} w. \end{align}
1.3. Cones, solid angles, and intrinsic volumes
The function ![]() $g_n$
has appeared (in many different parametrizations) in connection with internal and external angles of regular simplices and generalized orthants, but the results are somewhat scattered through the literature, and especially the properties of
$g_n$
has appeared (in many different parametrizations) in connection with internal and external angles of regular simplices and generalized orthants, but the results are somewhat scattered through the literature, and especially the properties of ![]() $g_n(r)$
at negative values of r do not seem to be widely known. In the following two sections we shall provide an overview of what is known about
$g_n(r)$
at negative values of r do not seem to be widely known. In the following two sections we shall provide an overview of what is known about ![]() $g_n$
, state some new results, and fix the notation needed for the proof of Theorem 1.1.
$g_n$
, state some new results, and fix the notation needed for the proof of Theorem 1.1.
A non-empty subset ![]() $C\subset \mathbb{R}^N$
is called a convex cone if for every
$C\subset \mathbb{R}^N$
is called a convex cone if for every ![]() $x,y\in C$
and
$x,y\in C$
and ![]() $\lambda,\mu>0$
we have
$\lambda,\mu>0$
we have ![]() $\lambda x + \mu y\in C$
. In the following we restrict our attention to polyhedral cones (or just cones, for short), which are defined as intersections of finitely many closed half-spaces whose boundaries contain the origin. The linear hull of C, i.e. the smallest linear space containing C, is denoted by L(C). Letting Z be a standard Gaussian random vector on L(C), the solid angle of the cone C is defined as
$\lambda x + \mu y\in C$
. In the following we restrict our attention to polyhedral cones (or just cones, for short), which are defined as intersections of finitely many closed half-spaces whose boundaries contain the origin. The linear hull of C, i.e. the smallest linear space containing C, is denoted by L(C). Letting Z be a standard Gaussian random vector on L(C), the solid angle of the cone C is defined as
In fact, the same formula remains true if Z has any rotationally invariant distribution on L(C). Note that we measure the solid angle with respect to the linear hull L(C) as the ambient space, so that the solid angle is never 0, even for cones with empty interior.
Denote the standard scalar product on ![]() $\mathbb{R}^N$
by
$\mathbb{R}^N$
by ![]() $\langle\cdot,\cdot\rangle$
and let
$\langle\cdot,\cdot\rangle$
and let ![]() $e_1,\ldots,e_{N}$
be the standard basis of
$e_1,\ldots,e_{N}$
be the standard basis of ![]() $\mathbb{R}^{N}$
. Fix any
$\mathbb{R}^{N}$
. Fix any ![]() $r\geq -1/n$
and consider n vectors
$r\geq -1/n$
and consider n vectors ![]() $u_1,\ldots,u_n$
in
$u_1,\ldots,u_n$
in ![]() $\mathbb{R}^N$
,
$\mathbb{R}^N$
, ![]() $n\leq N$
, such that
$n\leq N$
, such that
 \begin{equation*}\langle u_i, u_j\rangle=\begin{cases}1+r &\text{ if } i=j,\\[4pt]
r &\text{ if } i\neq j,\end{cases}\quad i,j\in \{1,\ldots,n\}.\end{equation*}
\begin{equation*}\langle u_i, u_j\rangle=\begin{cases}1+r &\text{ if } i=j,\\[4pt]
r &\text{ if } i\neq j,\end{cases}\quad i,j\in \{1,\ldots,n\}.\end{equation*}
Denote the cone spanned by the vectors ![]() $u_1,\ldots,u_n$
by
$u_1,\ldots,u_n$
by
The specific choice of the vectors ![]() $u_1,\ldots,u_n$
as well as the dimension N of the ambient space will be of minor importance because we are interested in the isometry type of the cone only. For
$u_1,\ldots,u_n$
as well as the dimension N of the ambient space will be of minor importance because we are interested in the isometry type of the cone only. For ![]() $r=0$
, the cone
$r=0$
, the cone ![]() $C_n(0)$
is isometric to the positive orthant
$C_n(0)$
is isometric to the positive orthant ![]() $\mathbb{R}_+^n$
. Vershik and Sporyshev [Reference Vershik and Sporyshev30] called
$\mathbb{R}_+^n$
. Vershik and Sporyshev [Reference Vershik and Sporyshev30] called ![]() $C_n(r)$
the contracted (respectively, extended) orthant if
$C_n(r)$
the contracted (respectively, extended) orthant if ![]() $r<0$
(respectively,
$r<0$
(respectively, ![]() $r>0$
). The extremal cases
$r>0$
). The extremal cases ![]() $r\to \infty$
and
$r\to \infty$
and ![]() $r=-1/n$
correspond to a ray and a half-space, respectively.
$r=-1/n$
correspond to a ray and a half-space, respectively.
Proposition 1.1. For all ![]() $r > -1/n$
, the solid angle of the cone
$r > -1/n$
, the solid angle of the cone ![]() $C_n(r)$
is given by
$C_n(r)$
is given by
This fact can be used to relate ![]() $g_n(r)$
to the volume of a regular spherical simplex. These volumes have been much studied since Schläfli [Reference Schläfli26].
$g_n(r)$
to the volume of a regular spherical simplex. These volumes have been much studied since Schläfli [Reference Schläfli26].
Theorem 1.3. Let ![]() $S_n(\ell)$
be a regular spherical simplex, with n vertices and side length
$S_n(\ell)$
be a regular spherical simplex, with n vertices and side length ![]() $\ell$
, on the unit sphere
$\ell$
, on the unit sphere ![]() $\mathbb{S}^{n-1}$
. That is, the geodesic distance between any two vertices of the simplex is
$\mathbb{S}^{n-1}$
. That is, the geodesic distance between any two vertices of the simplex is ![]() $\ell\in (0, \arccos ({-}\frac 1 {n-1}))$
. Then the spherical volume of
$\ell\in (0, \arccos ({-}\frac 1 {n-1}))$
. Then the spherical volume of ![]() $S_n(\ell)$
is given by
$S_n(\ell)$
is given by
More concretely, writing ![]() $r_*\coloneqq -\frac{\cos \ell}{1+ (n-1)\cos \ell}$
, we have
$r_*\coloneqq -\frac{\cos \ell}{1+ (n-1)\cos \ell}$
, we have
 \begin{align}\mathop{\mathrm{Vol}}\nolimits_{n-1}({S_n(\ell)}) &= \frac{2}{\Gamma(\frac n2) \sqrt \pi} \int_\infty^{\infty} \left(\int_{-\infty}^{x\sqrt{r_*}}{\rm e}^{-z^2} {\rm d} z\right)^n {\rm e}^{-x^2} {\rm d} x \quad\text{if } -\frac{1}{n-1}
< \cos \ell \leq 0;\nonumber\\ \end{align}
\begin{align}\mathop{\mathrm{Vol}}\nolimits_{n-1}({S_n(\ell)}) &= \frac{2}{\Gamma(\frac n2) \sqrt \pi} \int_\infty^{\infty} \left(\int_{-\infty}^{x\sqrt{r_*}}{\rm e}^{-z^2} {\rm d} z\right)^n {\rm e}^{-x^2} {\rm d} x \quad\text{if } -\frac{1}{n-1}
< \cos \ell \leq 0;\nonumber\\ \end{align}
 \begin{align}\mathop{\mathrm{Vol}}\nolimits_{n-1}({S_n(\ell)}) &=\frac {2}{\sqrt{\pi}} \int_0^{\infty} \operatorname{Re} \left[\left(\frac 12 + \frac{i}{\sqrt{\pi}} \int_0^{x\sqrt{-r_*} } {\rm e}^{z^2} {\rm d} z\right)^n\right]{\rm e}^{-x^2}{\rm d} x \quad \text{if } \cos \ell\geq 0.\nonumber\\ \end{align}
\begin{align}\mathop{\mathrm{Vol}}\nolimits_{n-1}({S_n(\ell)}) &=\frac {2}{\sqrt{\pi}} \int_0^{\infty} \operatorname{Re} \left[\left(\frac 12 + \frac{i}{\sqrt{\pi}} \int_0^{x\sqrt{-r_*} } {\rm e}^{z^2} {\rm d} z\right)^n\right]{\rm e}^{-x^2}{\rm d} x \quad \text{if } \cos \ell\geq 0.\nonumber\\ \end{align}
Proof. Let ![]() $u_1,\ldots, u_n$
be as above. Observe that
$u_1,\ldots, u_n$
be as above. Observe that ![]() $u_1/\sqrt{1+r},\ldots,u_n/\sqrt{1+r}$
can be viewed as vertices of
$u_1/\sqrt{1+r},\ldots,u_n/\sqrt{1+r}$
can be viewed as vertices of ![]() $S_n(\arccos \frac{r}{1+r})$
. So, choose
$S_n(\arccos \frac{r}{1+r})$
. So, choose ![]() $r > -1/n$
such that
$r > -1/n$
such that ![]() $\ell = \arccos \frac{r}{1+r}$
. Then
$\ell = \arccos \frac{r}{1+r}$
. Then ![]() $r=\frac{\cos \ell} {1-\cos \ell}$
and
$r=\frac{\cos \ell} {1-\cos \ell}$
and
by Proposition 1.1.
Formula (1.15) can be found in the book of Böhm and Hertel [Reference Böhm and Hertel8, Satz 3, p. 283] or in the works of Ruben [Reference Ruben25], and [Reference Ruben24] and Hadwiger [Reference Hadwiger14]. Note that [Reference Böhm and Hertel8] uses a different parametrization for ![]() $S_n(\ell)$
; see [Reference Böhm and Hertel8, Satz 2, p. 277] for the relation between both parametrizations. Observe also that the Schläfli function
$S_n(\ell)$
; see [Reference Böhm and Hertel8, Satz 2, p. 277] for the relation between both parametrizations. Observe also that the Schläfli function ![]() $\textbf{f}^{(n)}(\alpha)$
used in [Reference Böhm and Hertel8] is related to
$\textbf{f}^{(n)}(\alpha)$
used in [Reference Böhm and Hertel8] is related to ![]() $g_n$
via
$g_n$
via
as one can see by comparing [Reference Böhm and Hertel8, Satz 2, p. 279] with Theorem 1.3. The case ![]() $\cos \ell >0$
is missing in [Reference Böhm and Hertel8] and in many other references on the subject. Formula (1.16) was proved by Vershik and Sporyshev [Reference Vershik and Sporyshev30, Corollary 3, p. 192]; see also [Reference Böröczky and Henk9], [Reference Donoho and Tanner12], and [Reference Donoho and Tanner11] for asymptotic results.
$\cos \ell >0$
is missing in [Reference Böhm and Hertel8] and in many other references on the subject. Formula (1.16) was proved by Vershik and Sporyshev [Reference Vershik and Sporyshev30, Corollary 3, p. 192]; see also [Reference Böröczky and Henk9], [Reference Donoho and Tanner12], and [Reference Donoho and Tanner11] for asymptotic results.
To proceed, we need to recall some notions related to solid angles. A polyhedral set is an intersection of finitely many closed half-spaces (whose boundaries need not pass through the origin). If a polyhedral set is bounded, it is called a polytope. Polyhedral cones are special cases of polyhedral sets. Denote by ![]() $\mathcal{F}_k(P)$
the set of k-dimensional faces of a polyhedral set P. The tangent cone at a face
$\mathcal{F}_k(P)$
the set of k-dimensional faces of a polyhedral set P. The tangent cone at a face ![]() $F\in \mathcal{F}_k(P)$
is defined by
$F\in \mathcal{F}_k(P)$
is defined by
where ![]() $f_0$
is any point in the relative interior of F, i.e. the interior of F taken with respect to its affine hull. The normal cone at the face
$f_0$
is any point in the relative interior of F, i.e. the interior of F taken with respect to its affine hull. The normal cone at the face ![]() $F\in \mathcal{F}_k(P)$
is defined as the polar of the tangent cone, that is,
$F\in \mathcal{F}_k(P)$
is defined as the polar of the tangent cone, that is,
For certain special values of r one can interpret ![]() $g_n(r)$
as inner or normal solid angles at the faces of the regular simplex. The inner and normal (or external) solid angles of P at F are defined as the solid angles of the cones
$g_n(r)$
as inner or normal solid angles at the faces of the regular simplex. The inner and normal (or external) solid angles of P at F are defined as the solid angles of the cones ![]() $T_F(P)$
and
$T_F(P)$
and ![]() $N_F(P)$
, respectively.
$N_F(P)$
, respectively.
Proposition 1.2. Let ![]() $\Delta_n\coloneqq \mathop{\mathrm{conv}}\nolimits(e_1,\ldots,e_n)$
be the
$\Delta_n\coloneqq \mathop{\mathrm{conv}}\nolimits(e_1,\ldots,e_n)$
be the ![]() $(n-1)$
-dimensional regular simplex in
$(n-1)$
-dimensional regular simplex in ![]() $\mathbb{R}^n$
.
$\mathbb{R}^n$
.
(a) The normal solid angle at any
 $(k-1)$
-dimensional face of
$(k-1)$
-dimensional face of  $\Delta_n$
equals
$\Delta_n$
equals  \begin{equation*}g_{n-k}\left(\frac 1k\right) = \frac {1}{\sqrt{\pi}} \int_{-\infty}^{\infty} \left(\frac{1}{\sqrt{\pi}} \int_{-\infty}^{x/\sqrt{k}} {\rm e}^{-z^2} {\rm d} z\right)^{n-k}{\rm e}^{-x^2}{\rm d} x.\end{equation*}
\begin{equation*}g_{n-k}\left(\frac 1k\right) = \frac {1}{\sqrt{\pi}} \int_{-\infty}^{\infty} \left(\frac{1}{\sqrt{\pi}} \int_{-\infty}^{x/\sqrt{k}} {\rm e}^{-z^2} {\rm d} z\right)^{n-k}{\rm e}^{-x^2}{\rm d} x.\end{equation*}
(b) The inner solid angle at any
 $(k-1)$
-dimensional face of
$(k-1)$
-dimensional face of  $\Delta_n$
equals
$\Delta_n$
equals  \begin{equation*}g_{n-k}\left({-}\frac 1n\right) =\frac {2}{\sqrt{\pi}} \int_0^{\infty} \operatorname{Re} \left[\left(\frac 12 + \frac{i}{\sqrt{\pi}} \int_0^{x/\sqrt{n}} {\rm e}^{z^2} {\rm d} z\right)^{n-k}\right]{\rm e}^{-x^2}{\rm d} x.\end{equation*}
\begin{equation*}g_{n-k}\left({-}\frac 1n\right) =\frac {2}{\sqrt{\pi}} \int_0^{\infty} \operatorname{Re} \left[\left(\frac 12 + \frac{i}{\sqrt{\pi}} \int_0^{x/\sqrt{n}} {\rm e}^{z^2} {\rm d} z\right)^{n-k}\right]{\rm e}^{-x^2}{\rm d} x.\end{equation*}
Both parts were previously known; see [Reference Hadwiger14], and [Reference Ruben25] for part (a) and [23, Section 4] (where the method used was attributed to H. E. Daniels) as well as [Reference Vershik and Sporyshev30, Lemma 4] for part (b). A formula for the normal solid angles of crosspolytopes (which is similar to part (a)) was derived in [Reference Betke and Henk6].
The next proposition provides a geometric interpretation of ![]() $b_{n,k}(\sigma^2)$
. The kth conic intrinsic volume of a cone C is given by
$b_{n,k}(\sigma^2)$
. The kth conic intrinsic volume of a cone C is given by
where we recall that ![]() $\alpha(F)$
is the solid angle of the cone F measured with respect to the linear hull of F. See [Reference Amelunxen and Lotz4] for equivalent definitions and properties.
$\alpha(F)$
is the solid angle of the cone F measured with respect to the linear hull of F. See [Reference Amelunxen and Lotz4] for equivalent definitions and properties.
Proposition 1.3. For every ![]() $r > -1/n$
and
$r > -1/n$
and ![]() $k\in \{0,\ldots,n\}$
, the kth conic intrinsic volume of the cone
$k\in \{0,\ldots,n\}$
, the kth conic intrinsic volume of the cone ![]() $C_n(r)$
is given by
$C_n(r)$
is given by
Remark 1.1. As a consequence of the Gauss–Bonnet formula for conic intrinsic volumes (see [Reference Schneider and Weil28, Theorem 6.5.5] or [Reference Amelunxen and Lotz4, Corollary 4.4]), we obtain the identities
 \begin{equation*}\sum_{k=0}^{\lfloor n/2 \rfloor} b_{n,2k}(r) = \sum_{k=0}^{\lfloor (n-1)/2\rfloor} b_{n,2k+1}(r) = \frac 12.\end{equation*}
\begin{equation*}\sum_{k=0}^{\lfloor n/2 \rfloor} b_{n,2k}(r) = \sum_{k=0}^{\lfloor (n-1)/2\rfloor} b_{n,2k+1}(r) = \frac 12.\end{equation*}
In particular, the numbers ![]() $b_{n,0}(r), \ldots, b_{n,n}(r)$
define a probability distribution on
$b_{n,0}(r), \ldots, b_{n,n}(r)$
define a probability distribution on ![]() $\{0,\ldots,n\}$
, a fact which is not evident in view of the expression for
$\{0,\ldots,n\}$
, a fact which is not evident in view of the expression for ![]() $g_n$
given in (1.7) and (1.8). For
$g_n$
given in (1.7) and (1.8). For ![]() $r=0$
(in which case
$r=0$
(in which case ![]() $C_n(0)$
is the positive orthant
$C_n(0)$
is the positive orthant ![]() $\mathbb{R}^n_+$
) this distribution reduces to the binomial one with parameters
$\mathbb{R}^n_+$
) this distribution reduces to the binomial one with parameters ![]() $(n, 1/2)$
, because
$(n, 1/2)$
, because ![]() $g_n(0)= 2^{-n}$
by Proposition 1.4 (d) below.
$g_n(0)= 2^{-n}$
by Proposition 1.4 (d) below.
1.4. Properties of  $\mathbf{g}_\mathbf{n}$
$\mathbf{g}_\mathbf{n}$
Next we give a formula for ![]() $g_n(r)$
which may be more convenient than its definition (1.4). Recall that
$g_n(r)$
which may be more convenient than its definition (1.4). Recall that ![]() $\Phi$
denotes the standard normal distribution function (see (1.6)), viewed as an analytic function on the entire complex plane.
$\Phi$
denotes the standard normal distribution function (see (1.6)), viewed as an analytic function on the entire complex plane.
Proposition 1.4. The function ![]() $g_n\,:\, [-\frac 1n,\infty) \to [0,1]$
defined in (1.4) has the following properties.
$g_n\,:\, [-\frac 1n,\infty) \to [0,1]$
defined in (1.4) has the following properties.
(a) For all
 $n\in\mathbb{N}$
and
$n\in\mathbb{N}$
and  $r\geq -\frac 1n$
,
(1.19)where, in the case of negative r, we use the convention
$r\geq -\frac 1n$
,
(1.19)where, in the case of negative r, we use the convention \begin{align}g_n(r)&=\frac 1 {\sqrt {2\pi}} \int_{-\infty}^{\infty} \Phi^n (\sqrt r x) {\rm e}^{-x^2/2} {\rm d} x\notag \\[5pt]
&=\frac 1 {\sqrt {2\pi}} \int_{0}^{\infty} \left(\Phi^n (\sqrt r x) + \Phi^n ({-}\sqrt r x)\right) {\rm e}^{-x^2/2} {\rm d} x,\end{align}
\begin{align}g_n(r)&=\frac 1 {\sqrt {2\pi}} \int_{-\infty}^{\infty} \Phi^n (\sqrt r x) {\rm e}^{-x^2/2} {\rm d} x\notag \\[5pt]
&=\frac 1 {\sqrt {2\pi}} \int_{0}^{\infty} \left(\Phi^n (\sqrt r x) + \Phi^n ({-}\sqrt r x)\right) {\rm e}^{-x^2/2} {\rm d} x,\end{align}
 $\sqrt{r} = i \sqrt{-r}$
. In fact, the rightmost expression in (1.19) defines
$\sqrt{r} = i \sqrt{-r}$
. In fact, the rightmost expression in (1.19) defines  $g_n$
as an analytic function on the half-plane
$g_n$
as an analytic function on the half-plane  $\operatorname{Re} r>-\frac 1n$
.
$\operatorname{Re} r>-\frac 1n$
.(b) For all
 $n\in \{2,3,\ldots\}$
and
$n\in \{2,3,\ldots\}$
and  $r> -\frac 1n$
we have
$r> -\frac 1n$
we have  \begin{equation*}g^{\prime}_{n}(r) = \frac{n(n-1)}{4\pi (r+1)\sqrt{2r+1}} g_{n-2} \left(\frac{r}{2r+1}\right).\end{equation*}
\begin{equation*}g^{\prime}_{n}(r) = \frac{n(n-1)}{4\pi (r+1)\sqrt{2r+1}} g_{n-2} \left(\frac{r}{2r+1}\right).\end{equation*}
(c)
 $g_0(r) = 1$
(by definition) and
$g_0(r) = 1$
(by definition) and  $g_1(r) = \frac 12$
.
$g_1(r) = \frac 12$
.(d) For every
 $n\in\mathbb{N}$
, we have
$n\in\mathbb{N}$
, we have  \begin{equation*}g_n(0) = 2^{-n},\;\;\;g_n(1) = \frac 1 {n+1},\;\;\;\lim_{r\to+\infty}g_n(r)= \frac 12.\end{equation*}
\begin{equation*}g_n(0) = 2^{-n},\;\;\;g_n(1) = \frac 1 {n+1},\;\;\;\lim_{r\to+\infty}g_n(r)= \frac 12.\end{equation*}
(e) For
 $n\in \{2,3,\ldots\}$
we have
$n\in \{2,3,\ldots\}$
we have  $g_n({-}\frac 1n) = 0$
.
$g_n({-}\frac 1n) = 0$
.(f)
 $g_2(r) = \frac 14 + \frac 1{2\pi} \arcsin \frac{r}{1+r}$
and
$g_2(r) = \frac 14 + \frac 1{2\pi} \arcsin \frac{r}{1+r}$
and  $g_3(r) = \frac 18 + \frac 3{4\pi} \arcsin \frac{r}{1+r}$
.
$g_3(r) = \frac 18 + \frac 3{4\pi} \arcsin \frac{r}{1+r}$
.(g) For every fixed
 $n\in\mathbb{N}$
we have
$n\in\mathbb{N}$
we have  \begin{equation*}g_n\left( -\frac 1n + \varepsilon\right) \sim \frac{n^n \Gamma(n/2)}{2 \, \pi^{n/2} \Gamma(n) \sqrt n} \cdot \varepsilon^{(n-1)/2}, \quad \varepsilon \downarrow 0.\end{equation*}
\begin{equation*}g_n\left( -\frac 1n + \varepsilon\right) \sim \frac{n^n \Gamma(n/2)}{2 \, \pi^{n/2} \Gamma(n) \sqrt n} \cdot \varepsilon^{(n-1)/2}, \quad \varepsilon \downarrow 0.\end{equation*}
(h) For all
 $n\in\mathbb{N}$
, the functions
$n\in\mathbb{N}$
, the functions  $g_{2n}$
and
$g_{2n}$
and  $g_{2n+1}$
admit extensions to analytic functions on some unramified cover of
$g_{2n+1}$
admit extensions to analytic functions on some unramified cover of  $\mathbb{C}\backslash \{-1/k\colon k=1,\ldots, 2n\}$
.
$\mathbb{C}\backslash \{-1/k\colon k=1,\ldots, 2n\}$
.
Remark 1.2. Special values of ![]() $g_n$
listed in Parts (d) and (e) were known to Schläfli [Reference Schläfli26, p. 267]; see also [Reference Böhm and Hertel8, pp. 285–286]. Part (b) is a consequence of the Schläfli differential relation; see Böhm and Hertel [Reference Böhm and Hertel8, Satz 2, p. 279]. For completeness, we shall provide a self-contained proof of Proposition 1.4 in Section 3.1.
$g_n$
listed in Parts (d) and (e) were known to Schläfli [Reference Schläfli26, p. 267]; see also [Reference Böhm and Hertel8, pp. 285–286]. Part (b) is a consequence of the Schläfli differential relation; see Böhm and Hertel [Reference Böhm and Hertel8, Satz 2, p. 279]. For completeness, we shall provide a self-contained proof of Proposition 1.4 in Section 3.1.
Remark 1.3. Using the fact that ![]() $\overline{\Phi(iz)} = \Phi({-}iz)$
for
$\overline{\Phi(iz)} = \Phi({-}iz)$
for ![]() $z\in\mathbb{R}$
, one can state (1.19) in the case of real
$z\in\mathbb{R}$
, one can state (1.19) in the case of real ![]() $r \in [-\frac 1n, 0]$
as follows:
$r \in [-\frac 1n, 0]$
as follows:
 \begin{align*}g_n(r)&=\frac 2 {\sqrt {2\pi}} \int_{0}^{\infty} \operatorname{Re}(\Phi^n ( i \sqrt {-r} x)) {\rm e}^{-x^2/2} {\rm d} x\\[4pt]
&=\frac {2}{\sqrt{\pi}} \int_0^{\infty} \operatorname{Re} \left[\left(\frac 12 + \frac{i}{\sqrt{\pi}} \int_0^{x\sqrt{-r}} {\rm e}^{z^2} {\rm d} z\right)^n\right]{\rm e}^{-x^2}{\rm d} x, \end{align*}
\begin{align*}g_n(r)&=\frac 2 {\sqrt {2\pi}} \int_{0}^{\infty} \operatorname{Re}(\Phi^n ( i \sqrt {-r} x)) {\rm e}^{-x^2/2} {\rm d} x\\[4pt]
&=\frac {2}{\sqrt{\pi}} \int_0^{\infty} \operatorname{Re} \left[\left(\frac 12 + \frac{i}{\sqrt{\pi}} \int_0^{x\sqrt{-r}} {\rm e}^{z^2} {\rm d} z\right)^n\right]{\rm e}^{-x^2}{\rm d} x, \end{align*}
a formula obtained by Vershik and Sporyshev [30, Corollary 3, p. 192].
Remark 1.4. Taking ![]() $r=-1/n$
in (1.19), making the change of variables
$r=-1/n$
in (1.19), making the change of variables ![]() $y=x/\sqrt n$
, and using that
$y=x/\sqrt n$
, and using that ![]() $g_n({-}1/n) = 0$
for
$g_n({-}1/n) = 0$
for ![]() $n\geq 2$
, we obtain the curious identity
$n\geq 2$
, we obtain the curious identity
Using induction and partial integration we shall extend this as follows.
Proposition 1.5. For all ![]() $m\in\mathbb{N}_0$
and all
$m\in\mathbb{N}_0$
and all ![]() $n = m+2,m+3,\ldots$
we have
$n = m+2,m+3,\ldots$
we have
Also, for all ![]() $m\in\mathbb{N}_0$
we have
$m\in\mathbb{N}_0$
we have
For ![]() $n\leq m+1$
the integral in (1.21) diverges since
$n\leq m+1$
the integral in (1.21) diverges since ![]() $\Phi(iy) \sim \frac1 {\sqrt{2\pi} iy}{\rm e}^{y^2/2}$
as
$\Phi(iy) \sim \frac1 {\sqrt{2\pi} iy}{\rm e}^{y^2/2}$
as ![]() $y\to\infty$
,
$y\to\infty$
, ![]() $y\in\mathbb{R}$
; see [Reference Abramowitz and Stegun1, Eq. 7.1.23, p. 298]. Equation (1.22) states a formula for the Cauchy principal value which is well defined for
$y\in\mathbb{R}$
; see [Reference Abramowitz and Stegun1, Eq. 7.1.23, p. 298]. Equation (1.22) states a formula for the Cauchy principal value which is well defined for ![]() $n=m+1$
.
$n=m+1$
.
1.5. Expected number of k-faces
Let ![]() $f_k(\mathcal{P}_{n,d})$
be the number of k-dimensional faces of the Gaussian polytope
$f_k(\mathcal{P}_{n,d})$
be the number of k-dimensional faces of the Gaussian polytope ![]() $\mathcal{P}_{n,d}$
. Recall the notation
$\mathcal{P}_{n,d}$
. Recall the notation ![]() $p_{n,d} (\sigma^2) = \mathbb{P}[\sigma X \notin \mathcal{P}_{n,d}]$
, where X is a standard normal vector in
$p_{n,d} (\sigma^2) = \mathbb{P}[\sigma X \notin \mathcal{P}_{n,d}]$
, where X is a standard normal vector in ![]() $\mathbb{R}^d$
independent of
$\mathbb{R}^d$
independent of ![]() $\mathcal{P}_{n,d}$
. With the aid of the Blaschke–Petkantschin formula, Hug et al. [Reference Hug, Munsonius and Reitzner16, Theorem 3.2] showed that
$\mathcal{P}_{n,d}$
. With the aid of the Blaschke–Petkantschin formula, Hug et al. [Reference Hug, Munsonius and Reitzner16, Theorem 3.2] showed that
Using this formula, they proved an asymptotic result of the form
where ![]() $\bar c_{(k,d)}$
is an explicit constant only depending on d and k. With the aid of Theorem 1.1 one can derive the following explicit formula.
$\bar c_{(k,d)}$
is an explicit constant only depending on d and k. With the aid of Theorem 1.1 one can derive the following explicit formula.
Theorem 1.4. For every ![]() $k=0,\ldots, n-1$
we have
$k=0,\ldots, n-1$
we have
 \begin{equation}\mathbb E f_k ( \mathcal{P}_{n,d}) = \frac{2\cdot n!}{(k+1)!} \sum_{\substack{j= d - 2i > k\\i\in \mathbb{N}_0}} \frac{g_{j-1-k}\left({-}\frac 1j\right)g_{n-j}\left(\frac 1j\right)}{(\kern1.5pt j-1-k)!(n-j)!}.\end{equation}
\begin{equation}\mathbb E f_k ( \mathcal{P}_{n,d}) = \frac{2\cdot n!}{(k+1)!} \sum_{\substack{j= d - 2i > k\\i\in \mathbb{N}_0}} \frac{g_{j-1-k}\left({-}\frac 1j\right)g_{n-j}\left(\frac 1j\right)}{(\kern1.5pt j-1-k)!(n-j)!}.\end{equation}
Proof. Combine Theorem 1.1 with (1.23).
Remark 1.5. The quantities ![]() $g_{j-1-k}({-}\frac 1j)$
and
$g_{j-1-k}({-}\frac 1j)$
and ![]() $g_{n-j}(\frac 1j)$
appearing on the right-hand side of (1.25) are certain inner/normal solid angles of regular simplices; see Proposition 1.2. With this interpretation, the formula (1.25) is due to Affentranger and Schneider [Reference Affentranger and Schneider3].
$g_{n-j}(\frac 1j)$
appearing on the right-hand side of (1.25) are certain inner/normal solid angles of regular simplices; see Proposition 1.2. With this interpretation, the formula (1.25) is due to Affentranger and Schneider [Reference Affentranger and Schneider3].
Remark 1.6. More generally, Hug et al. [Reference Hug, Munsonius and Reitzner16] considered also the functional
which reduces to ![]() $f_{k} (\mathcal{P}_{n,d})$
for
$f_{k} (\mathcal{P}_{n,d})$
for ![]() $b=0$
. For
$b=0$
. For ![]() $k=d-1$
and
$k=d-1$
and ![]() $b=1$
one gets the surface area. Hug et al. [Reference Hug, Munsonius and Reitzner16] showed that
$b=1$
one gets the surface area. Hug et al. [Reference Hug, Munsonius and Reitzner16] showed that
 \begin{equation*}\mathbb E T^{d,k}_{0,b} (\mathcal{P}_{n,d}) = \mathbb E f_k ( \mathcal{P}_{n,d})\cdot \left(\frac{\sqrt {k+1}}{k!}\right)^b \prod_{j=1}^k \frac{\Gamma\left(\frac{d+b+1-j}{2}\right)}{\Gamma\left(\frac{d+1-j}{2}\right)}.\end{equation*}
\begin{equation*}\mathbb E T^{d,k}_{0,b} (\mathcal{P}_{n,d}) = \mathbb E f_k ( \mathcal{P}_{n,d})\cdot \left(\frac{\sqrt {k+1}}{k!}\right)^b \prod_{j=1}^k \frac{\Gamma\left(\frac{d+b+1-j}{2}\right)}{\Gamma\left(\frac{d+1-j}{2}\right)}.\end{equation*}
Thus, an explicit formula for ![]() $\mathbb E T^{d,k}_{0,b} (\mathcal{P}_{n,d})$
can be obtained from Theorem 1.4.
$\mathbb E T^{d,k}_{0,b} (\mathcal{P}_{n,d})$
can be obtained from Theorem 1.4.
The following fixed-r asymptotics for ![]() $g_n(r)=\frac 1 {\sqrt {2\pi}} \int_{-\infty}^{\infty} \Phi^n (\sqrt r x) {\rm e}^{-x^2/2} {\rm d} x$
was derived in [Reference Raynaud21, pp. 44–45] and [Reference Vershik and Sporyshev29, Lemma 5].
$g_n(r)=\frac 1 {\sqrt {2\pi}} \int_{-\infty}^{\infty} \Phi^n (\sqrt r x) {\rm e}^{-x^2/2} {\rm d} x$
was derived in [Reference Raynaud21, pp. 44–45] and [Reference Vershik and Sporyshev29, Lemma 5].
Proposition 1.6. For any fixed ![]() $r>0$
we have
$r>0$
we have
This can be used to compute the large-n asymptotics of the probability that ![]() $\sigma X \notin \mathcal{P}_{n,d}$
.
$\sigma X \notin \mathcal{P}_{n,d}$
.
Corollary 1.2. Fix any ![]() $\sigma^2>0$
and write
$\sigma^2>0$
and write ![]() $r=\frac{\sigma^2}{1+(d-1)\sigma^2}$
. Then
$r=\frac{\sigma^2}{1+(d-1)\sigma^2}$
. Then
Proof. It follows from Proposition 1.6 and (1.10) that for every fixed ![]() $k\in\mathbb{N}_0$
and
$k\in\mathbb{N}_0$
and ![]() $\sigma^2>0$
,
$\sigma^2>0$
,
In particular, ![]() $b_{n,d-m} (\sigma^2) = o(b_{n, d-1}(\sigma^2))$
for all
$b_{n,d-m} (\sigma^2) = o(b_{n, d-1}(\sigma^2))$
for all ![]() $m\geq 2$
and as
$m\geq 2$
and as ![]() $n\to\infty$
. Theorem 1.1 yields
$n\to\infty$
. Theorem 1.1 yields ![]() $p_{n,d}(\sigma^2) \sim 2 b_{n,d-1} (\sigma^2)$
, from which the required asymptotics follows.
$p_{n,d}(\sigma^2) \sim 2 b_{n,d-1} (\sigma^2)$
, from which the required asymptotics follows.
Remark 1.7. Applying Corollary 1.2 to the right-hand side of (1.23) we deduce the asymptotic formula
 \begin{align*}\mathbb E f_k ( \mathcal{P}_{n,d})&=\binom{n}{k+1} p_{n-k-1, d-k}\left(\frac 1 {k+1}\right)\\[5pt]
&\underset{n \to \infty}{\sim} \frac{2}{\sqrt d} \binom d{k+1} g_{d-1-k} \left({-}\frac 1d\right) (4\pi \log n)^{(d-1)/2},\end{align*}
\begin{align*}\mathbb E f_k ( \mathcal{P}_{n,d})&=\binom{n}{k+1} p_{n-k-1, d-k}\left(\frac 1 {k+1}\right)\\[5pt]
&\underset{n \to \infty}{\sim} \frac{2}{\sqrt d} \binom d{k+1} g_{d-1-k} \left({-}\frac 1d\right) (4\pi \log n)^{(d-1)/2},\end{align*}
which recovers a result of Affentranger [Reference Affentranger2] (see also [Reference Affentranger and Schneider3], [Reference Baryshnikov and Vitale5], and [Reference Hug, Munsonius and Reitzner16]) stated in (1.2).
1.6. Expected volume
Let us derive from our results the following formula for the expected volume of the Gaussian polytope, due to Efron [Reference Efron13]:
 \begin{equation}\mathbb E \mathop{\mathrm{Vol}}\nolimits_d (\mathcal{P}_{n,d}) = \frac {\pi^{\frac d2}}{\Gamma(\frac d2 +1)} \cdot \frac{n!}{d! (n-d-1)!} \int_{-\infty}^{\infty} \Phi^{n-d-1}(t) \varphi^{d+1} (t) {\rm d} t.\end{equation}
\begin{equation}\mathbb E \mathop{\mathrm{Vol}}\nolimits_d (\mathcal{P}_{n,d}) = \frac {\pi^{\frac d2}}{\Gamma(\frac d2 +1)} \cdot \frac{n!}{d! (n-d-1)!} \int_{-\infty}^{\infty} \Phi^{n-d-1}(t) \varphi^{d+1} (t) {\rm d} t.\end{equation}
In fact, Efron [Reference Efron13] proved the formula for ![]() $d=2$
and stated it for general d; another proof (valid for arbitrary d) can be found in [Reference Kabluchko and Zaporozhets19].
$d=2$
and stated it for general d; another proof (valid for arbitrary d) can be found in [Reference Kabluchko and Zaporozhets19].
Since the surface measure of the unit sphere in ![]() $\mathbb{R}^d$
equals
$\mathbb{R}^d$
equals ![]() $\omega_d = 2\pi^{d/2}/\Gamma(d/2)$
, we can express the expected volume of the Gaussian polytope as follows:
$\omega_d = 2\pi^{d/2}/\Gamma(d/2)$
, we can express the expected volume of the Gaussian polytope as follows:
 \begin{align*}\mathbb E \mathop{\mathrm{Vol}}\nolimits_d (\mathcal{P}_{n,d})&=\int_0^\infty (1-f_{n,d} (r)) \frac{2\pi^{d/2}}{\Gamma(d/2)} r^{d-1} {\rm d} r\\[5pt]
&=\frac {(2\pi)^{d/2}}{\Gamma(d/2)}\int_0^\infty (1-f_{n,d} (\sqrt{2u})) u^{(d/2)-1}{\rm d} u,\end{align*}
\begin{align*}\mathbb E \mathop{\mathrm{Vol}}\nolimits_d (\mathcal{P}_{n,d})&=\int_0^\infty (1-f_{n,d} (r)) \frac{2\pi^{d/2}}{\Gamma(d/2)} r^{d-1} {\rm d} r\\[5pt]
&=\frac {(2\pi)^{d/2}}{\Gamma(d/2)}\int_0^\infty (1-f_{n,d} (\sqrt{2u})) u^{(d/2)-1}{\rm d} u,\end{align*}
where we have made the change of variables ![]() $r= \sqrt{2u}$
. On the other hand, by Corollary 1.1 together with the identity
$r= \sqrt{2u}$
. On the other hand, by Corollary 1.1 together with the identity ![]() $\sum_{k=0}^n b_{n,k}(1/\lambda) =1$
(see Remark 1.1), we can write
$\sum_{k=0}^n b_{n,k}(1/\lambda) =1$
(see Remark 1.1), we can write
for all ![]() $\lambda>0$
. Hence, by the monotone convergence theorem,
$\lambda>0$
. Hence, by the monotone convergence theorem,
Recall from (1.10) that for every fixed ![]() $k\in \{0,\ldots,n\}$
,
$k\in \{0,\ldots,n\}$
,
Clearly,
whereas Proposition 1.4 (g) yields
Taking everything together, we obtain
So, in the sum on the right-hand side of (1.27) the term ![]() $b_{n,d+1}(1/\lambda)\sim \text{const} \cdot \lambda^{d/2}$
dominates and we obtain
$b_{n,d+1}(1/\lambda)\sim \text{const} \cdot \lambda^{d/2}$
dominates and we obtain
 \begin{align*}\mathbb E \mathop{\mathrm{Vol}}\nolimits_d (\mathcal{P}_{n,d})&=(2\pi)^{d/2} \binom{n}{d+1} \frac{\Gamma(\frac{d+1}{2}) \sqrt{d+1}}{ \pi^{\frac {d+1}{2}} \Gamma(d+1)} g_{n-d-1}\left(\frac 1 {d+1}\right)\\[5pt]
&= \binom{n}{d+1} \frac{\sqrt{d+1}}{ 2^{\frac d2} \Gamma\left(\frac d2 + 1\right)} g_{n-d-1}\left(\frac 1 {d+1}\right),\end{align*}
\begin{align*}\mathbb E \mathop{\mathrm{Vol}}\nolimits_d (\mathcal{P}_{n,d})&=(2\pi)^{d/2} \binom{n}{d+1} \frac{\Gamma(\frac{d+1}{2}) \sqrt{d+1}}{ \pi^{\frac {d+1}{2}} \Gamma(d+1)} g_{n-d-1}\left(\frac 1 {d+1}\right)\\[5pt]
&= \binom{n}{d+1} \frac{\sqrt{d+1}}{ 2^{\frac d2} \Gamma\left(\frac d2 + 1\right)} g_{n-d-1}\left(\frac 1 {d+1}\right),\end{align*}
where we used the Legendre duplication formula. Recalling formula (1.19) for ![]() $g_n(r)$
, and performing some simple transformations, we arrive at (1.26). Proposition 1.6 yields the following asymptotic formula due to Affentranger [Reference Affentranger2, Theorem 4]:
$g_n(r)$
, and performing some simple transformations, we arrive at (1.26). Proposition 1.6 yields the following asymptotic formula due to Affentranger [Reference Affentranger2, Theorem 4]:
as ![]() $n\to\infty$
, while d stays fixed. A more refined asymptotics was derived in [Reference Kabluchko and Zaporozhets19].
$n\to\infty$
, while d stays fixed. A more refined asymptotics was derived in [Reference Kabluchko and Zaporozhets19].
1.7. Low-dimensional examples
Let ![]() $d=2$
. Theorem 1.1 simplifies to
$d=2$
. Theorem 1.1 simplifies to
 \begin{align*}\mathbb{P}[\sigma X \notin \mathop{\mathrm{conv}}\nolimits (X_1,\ldots,X_n)]&=2b_{n,1}(\sigma^2) = 2 n g_1\left({-}\frac{\sigma^2}{1+\sigma^2}\right) g_{n-1}\left(\frac{\sigma^2}{1+\sigma^2}\right)\\&=ng_{n-1}\left(\frac{\sigma^2}{1+\sigma^2}\right).\end{align*}
\begin{align*}\mathbb{P}[\sigma X \notin \mathop{\mathrm{conv}}\nolimits (X_1,\ldots,X_n)]&=2b_{n,1}(\sigma^2) = 2 n g_1\left({-}\frac{\sigma^2}{1+\sigma^2}\right) g_{n-1}\left(\frac{\sigma^2}{1+\sigma^2}\right)\\&=ng_{n-1}\left(\frac{\sigma^2}{1+\sigma^2}\right).\end{align*}
We obtain the formula
The next theorem gives an explicit formula for the non-absorption probability in the case ![]() $d=2$
.
$d=2$
.
Theorem 1.5. Let ![]() $\xi,\xi_1,\ldots,\xi_n$
be standard normal random variables and let W be a random variable with the arcsine density
$\xi,\xi_1,\ldots,\xi_n$
be standard normal random variables and let W be a random variable with the arcsine density ![]() $\frac{1}{\pi} (1-y^2)^{-1/2} {\rm d} y$
on
$\frac{1}{\pi} (1-y^2)^{-1/2} {\rm d} y$
on ![]() $[-1,1]$
, all variables being independent. Define
$[-1,1]$
, all variables being independent. Define ![]() $M_{k}= \max\{\xi_1,\ldots,\xi_{k}\}$
. Then, for all
$M_{k}= \max\{\xi_1,\ldots,\xi_{k}\}$
. Then, for all ![]() $u\geq 0$
,
$u\geq 0$
,
 \begin{align*}f_{n,2}(\sqrt{2u})&= \mathbb{P}[ M_{n}^2 + \xi^2 \leq 2u] + \frac {{\rm d}}{{\rm d} u}\mathbb{P}[ M_{n}^2 + \xi^2 \leq 2u]\\[5pt]
&= \mathbb{P}[ M_{n}^2 + \xi^2 \leq 2u] + n{\rm e}^{-u} \mathbb{P}[M_{n-1} \leq \sqrt{2u} W].\end{align*}
\begin{align*}f_{n,2}(\sqrt{2u})&= \mathbb{P}[ M_{n}^2 + \xi^2 \leq 2u] + \frac {{\rm d}}{{\rm d} u}\mathbb{P}[ M_{n}^2 + \xi^2 \leq 2u]\\[5pt]
&= \mathbb{P}[ M_{n}^2 + \xi^2 \leq 2u] + n{\rm e}^{-u} \mathbb{P}[M_{n-1} \leq \sqrt{2u} W].\end{align*}
That is, ![]() $f_{n,2}(\sqrt{2u})$
is the sum of the distribution function and the density of the random variable
$f_{n,2}(\sqrt{2u})$
is the sum of the distribution function and the density of the random variable ![]() $\frac 12 (M_n^2+\xi^2)$
at u.
$\frac 12 (M_n^2+\xi^2)$
at u.
Two-dimensional absorption probabilities were studied in a very general setting by Jewell and Romano [Reference Jewell and Romano17], and [Reference Jewell and Romano18], but their method does not seem to yield an explicit formula like that in Theorem 1.5.
Consider now the case ![]() $d=3$
. Using first Theorem 1.1, (1.10), and then Proposition 1.4, we arrive at
$d=3$
. Using first Theorem 1.1, (1.10), and then Proposition 1.4, we arrive at
 \begin{align*}\lefteqn{\mathbb{P}[\sigma X \notin \mathop{\mathrm{conv}}\nolimits (X_1,\ldots,X_n)]}\\[3pt]
& \quad = 2b_{n,2}(\sigma^2) + 2b_{n,0}(\sigma^2)\\[3pt]
& \quad =n(n-1) g_2\left({-}\frac{\sigma^2}{1+2\sigma^2}\right) g_{n-2}\left(\frac{\sigma^2}{1+2\sigma^2}\right)+ 2 g_n(\sigma^2)\\[3pt]
& \quad =\frac{n(n-1)}{\sqrt{2\pi}}\left(\frac 14 - \frac 1{2\pi} \arcsin \frac{\sigma^2}{1+\sigma^2}\right)\int_{-\infty}^{+\infty} \Phi^{n-2} \left(\frac{\sigma x}{\sqrt{1+2\sigma^2}}\right) {\rm e}^{-x^2/2} {\rm d} x\\[3pt]
& \qquad + \frac {2}{\sqrt{2\pi}} \int_{-\infty}^{+\infty} \Phi^n (\sigma x) {\rm e}^{-x^2/2}{\rm d} x,\end{align*}
\begin{align*}\lefteqn{\mathbb{P}[\sigma X \notin \mathop{\mathrm{conv}}\nolimits (X_1,\ldots,X_n)]}\\[3pt]
& \quad = 2b_{n,2}(\sigma^2) + 2b_{n,0}(\sigma^2)\\[3pt]
& \quad =n(n-1) g_2\left({-}\frac{\sigma^2}{1+2\sigma^2}\right) g_{n-2}\left(\frac{\sigma^2}{1+2\sigma^2}\right)+ 2 g_n(\sigma^2)\\[3pt]
& \quad =\frac{n(n-1)}{\sqrt{2\pi}}\left(\frac 14 - \frac 1{2\pi} \arcsin \frac{\sigma^2}{1+\sigma^2}\right)\int_{-\infty}^{+\infty} \Phi^{n-2} \left(\frac{\sigma x}{\sqrt{1+2\sigma^2}}\right) {\rm e}^{-x^2/2} {\rm d} x\\[3pt]
& \qquad + \frac {2}{\sqrt{2\pi}} \int_{-\infty}^{+\infty} \Phi^n (\sigma x) {\rm e}^{-x^2/2}{\rm d} x,\end{align*}
but we were unable to invert the Laplace transform to obtain a formula for ![]() $f_{n,3}$
similar to that of Theorem 1.5. Similarly, for
$f_{n,3}$
similar to that of Theorem 1.5. Similarly, for ![]() $d=4$
we obtain
$d=4$
we obtain
 \begin{align*}\lefteqn{\mathbb{P}[\sigma X \notin \mathop{\mathrm{conv}}\nolimits (X_1,\ldots,X_n)]}\\[5pt]
&= 2b_{n,3}(\sigma^2) + 2b_{n,1}(\sigma^2)\\[5pt]
&=\frac{n(n-1)(n-2)}{3} g_3\left({-}\frac{\sigma^2}{1+3\sigma^2}\right) g_{n-3}\left(\frac{\sigma^2}{1+3\sigma^2}\right) + ng_{n-1}\left(\frac{\sigma^2}{1+\sigma^2}\right)\\[5pt]
&=\frac{n(n-1)(n-2)}{3\sqrt{2\pi}}\left(\frac 18 - \frac 3{4\pi} \arcsin \frac{\sigma^2}{1+2\sigma^2}\right)\int_{-\infty}^{+\infty} \Phi^{n-3} \left(\frac{\sigma x}{\sqrt{1+3\sigma^2}}\right) {\rm e}^{-x^2/2} {\rm d} x\\[5pt]
&\phantom{=}+ \frac{n}{\sqrt{2\pi}}\int_{-\infty}^{+\infty} \Phi^{n-1} \left(\frac{\sigma x}{\sqrt{1+\sigma^2}}\right) {\rm e}^{-x^2/2} {\rm d} x.\end{align*}
\begin{align*}\lefteqn{\mathbb{P}[\sigma X \notin \mathop{\mathrm{conv}}\nolimits (X_1,\ldots,X_n)]}\\[5pt]
&= 2b_{n,3}(\sigma^2) + 2b_{n,1}(\sigma^2)\\[5pt]
&=\frac{n(n-1)(n-2)}{3} g_3\left({-}\frac{\sigma^2}{1+3\sigma^2}\right) g_{n-3}\left(\frac{\sigma^2}{1+3\sigma^2}\right) + ng_{n-1}\left(\frac{\sigma^2}{1+\sigma^2}\right)\\[5pt]
&=\frac{n(n-1)(n-2)}{3\sqrt{2\pi}}\left(\frac 18 - \frac 3{4\pi} \arcsin \frac{\sigma^2}{1+2\sigma^2}\right)\int_{-\infty}^{+\infty} \Phi^{n-3} \left(\frac{\sigma x}{\sqrt{1+3\sigma^2}}\right) {\rm e}^{-x^2/2} {\rm d} x\\[5pt]
&\phantom{=}+ \frac{n}{\sqrt{2\pi}}\int_{-\infty}^{+\infty} \Phi^{n-1} \left(\frac{\sigma x}{\sqrt{1+\sigma^2}}\right) {\rm e}^{-x^2/2} {\rm d} x.\end{align*}
Taking ![]() $\sigma=1$
in Theorem 1.1 yields the probability content of the Gaussian polytope, which is defined as
$\sigma=1$
in Theorem 1.1 yields the probability content of the Gaussian polytope, which is defined as
For ![]() $d=2,3,4$
we obtain the formulas
$d=2,3,4$
we obtain the formulas
 \begin{align*}C_{n,2} &= 1- \frac{n}{\sqrt{2\pi}}\int_{-\infty}^{+\infty} \Phi^{n-1} \left(\frac{x}{\sqrt{2}}\right) {\rm e}^{-x^2/2} {\rm d} x,\\[6pt]
C_{n,3} &= 1-\frac{n(n-1)}{6\sqrt{2\pi}}\int_{-\infty}^{+\infty} \Phi^{n-2} \left(\frac{x}{\sqrt 2}\right) {\rm e}^{-x^2/2} {\rm d} x - \frac {2}{n+1},\\[6pt]
C_{n,4} &= C_{n,2} -\frac{n(n-1)(n-2)}{3\sqrt{2\pi}} \left( \frac 18 - \frac 3{4\pi} \arcsin \frac 13\right)\int_{-\infty}^{+\infty} \Phi^{n-3} \left(\frac{x}{2}\right) {\rm e}^{-x^2/2} {\rm d} x.\end{align*}
\begin{align*}C_{n,2} &= 1- \frac{n}{\sqrt{2\pi}}\int_{-\infty}^{+\infty} \Phi^{n-1} \left(\frac{x}{\sqrt{2}}\right) {\rm e}^{-x^2/2} {\rm d} x,\\[6pt]
C_{n,3} &= 1-\frac{n(n-1)}{6\sqrt{2\pi}}\int_{-\infty}^{+\infty} \Phi^{n-2} \left(\frac{x}{\sqrt 2}\right) {\rm e}^{-x^2/2} {\rm d} x - \frac {2}{n+1},\\[6pt]
C_{n,4} &= C_{n,2} -\frac{n(n-1)(n-2)}{3\sqrt{2\pi}} \left( \frac 18 - \frac 3{4\pi} \arcsin \frac 13\right)\int_{-\infty}^{+\infty} \Phi^{n-3} \left(\frac{x}{2}\right) {\rm e}^{-x^2/2} {\rm d} x.\end{align*}
The formulas for ![]() $d=2,3$
were obtained by Efron [Reference Efron13], in Equations (7.5) and (7.6) on p. 341.
$d=2,3$
were obtained by Efron [Reference Efron13], in Equations (7.5) and (7.6) on p. 341.
1.8. Absorption probability in the Goodman–Pollack model
Let ![]() $v_1,\ldots,v_{n+1}$
be the vertices of an n-dimensional regular simplex inscribed into the unit sphere
$v_1,\ldots,v_{n+1}$
be the vertices of an n-dimensional regular simplex inscribed into the unit sphere ![]() $\mathbb S^{n-1} \subset \mathbb{R}^{n}$
. That is,
$\mathbb S^{n-1} \subset \mathbb{R}^{n}$
. That is, ![]() $|v_i|=1$
for all
$|v_i|=1$
for all ![]() $1\leq i\leq n+1$
and
$1\leq i\leq n+1$
and ![]() $\rho \coloneqq \langle v_i,v_j\rangle = -1/n$
for all
$\rho \coloneqq \langle v_i,v_j\rangle = -1/n$
for all ![]() $1\leq i < j \leq n+1$
. Let O be a random orthogonal matrix sampled according to the Haar probability measure on the orthogonal group O(n). Consider the randomly rotated regular simplex with vertices
$1\leq i < j \leq n+1$
. Let O be a random orthogonal matrix sampled according to the Haar probability measure on the orthogonal group O(n). Consider the randomly rotated regular simplex with vertices ![]() $Ov_1,\ldots,Ov_{n+1}$
and project it onto some fixed d-dimensional linear subspace
$Ov_1,\ldots,Ov_{n+1}$
and project it onto some fixed d-dimensional linear subspace ![]() $V_d\subset \mathbb{R}^{n}$
. The choice of
$V_d\subset \mathbb{R}^{n}$
. The choice of ![]() $V_d$
is irrelevant, so that we shall assume that
$V_d$
is irrelevant, so that we shall assume that ![]() $V_d\equiv \mathbb{R}^d$
is spanned by the first d vectors of the standard orthonormal basis
$V_d\equiv \mathbb{R}^d$
is spanned by the first d vectors of the standard orthonormal basis ![]() $e_1,\ldots,e_n$
of
$e_1,\ldots,e_n$
of ![]() $\mathbb{R}^{n}$
. Denote orthogonal projection onto
$\mathbb{R}^{n}$
. Denote orthogonal projection onto ![]() $V_d$
by
$V_d$
by ![]() $\Pi$
. The resulting random polytope
$\Pi$
. The resulting random polytope
is said to be distributed according to the Goodman–Pollack model. Affentranger and Schneider [Reference Affentranger and Schneider3] and Baryshnikov and Vitale [Reference Baryshnikov and Vitale5] observed that the Gaussian polytope ![]() $\mathcal{P}_{n+1,d}$
is closely related to the Goodman–Pollack polytope
$\mathcal{P}_{n+1,d}$
is closely related to the Goodman–Pollack polytope ![]() $\mathcal{Q}_{n+1,d}$
. In particular, Baryshnikov and Vitale [Reference Baryshnikov and Vitale5] showed that all functionals which remain invariant under affine transformations of the polytope (like the number of k-faces) have the same distribution in both models. We are interested in the non-absorption probability in the Goodman–Pollack model, that is,
$\mathcal{Q}_{n+1,d}$
. In particular, Baryshnikov and Vitale [Reference Baryshnikov and Vitale5] showed that all functionals which remain invariant under affine transformations of the polytope (like the number of k-faces) have the same distribution in both models. We are interested in the non-absorption probability in the Goodman–Pollack model, that is,
Clearly, this functional is not invariant with respect to the affine transformations of ![]() $\mathcal{Q}_{n,d}$
. We cannot compute the non-absorption probability explicitly, but it is possible to evaluate a certain integral transform of
$\mathcal{Q}_{n,d}$
. We cannot compute the non-absorption probability explicitly, but it is possible to evaluate a certain integral transform of ![]() $f_{n,d}^*$
.
$f_{n,d}^*$
.
Theorem 1.6. For every ![]() $\sigma^2\geq 0$
we have
$\sigma^2\geq 0$
we have
 \begin{equation*}\frac 1 {B\left(\frac d2, \frac{n-d}{2}\right)} \int_{0}^{\infty} \frac{u^{d-1}}{(1+u^2)^{n/2}} f_{n,d}^* \left(\sqrt{\frac{n\sigma^2 + 1}{n-1}} \cdot u\right) {\rm d} u = b_{n,d-1}(\sigma^2) + b_{n,d-3}(\sigma^2) +\ldots.\end{equation*}
\begin{equation*}\frac 1 {B\left(\frac d2, \frac{n-d}{2}\right)} \int_{0}^{\infty} \frac{u^{d-1}}{(1+u^2)^{n/2}} f_{n,d}^* \left(\sqrt{\frac{n\sigma^2 + 1}{n-1}} \cdot u\right) {\rm d} u = b_{n,d-1}(\sigma^2) + b_{n,d-3}(\sigma^2) +\ldots.\end{equation*}
Here, ![]() $B(\cdot, \cdot)$
denotes the Euler beta function. The proof of Theorem 1.6 will be given in Section 5.
$B(\cdot, \cdot)$
denotes the Euler beta function. The proof of Theorem 1.6 will be given in Section 5.
Remark 1.8. It is also possible to consider random projections ![]() $\mathcal{\tilde{Q}}_{n,d}$
of the random orthogonal transformation of the regular simplex
$\mathcal{\tilde{Q}}_{n,d}$
of the random orthogonal transformation of the regular simplex ![]() $\mathop{\mathrm{Conv}}\nolimits (e_1,\ldots,e_n)$
inscribed into the unit sphere
$\mathop{\mathrm{Conv}}\nolimits (e_1,\ldots,e_n)$
inscribed into the unit sphere ![]() $\mathbb{S}^{n-1} \subset \mathbb{R}^n$
. For the non-absorption probability
$\mathbb{S}^{n-1} \subset \mathbb{R}^n$
. For the non-absorption probability ![]() $\tilde f_{n,d}^*(|x|)\coloneqq \mathbb{P}[x\notin \mathcal{\tilde{Q}}_{n,d}]$
,
$\tilde f_{n,d}^*(|x|)\coloneqq \mathbb{P}[x\notin \mathcal{\tilde{Q}}_{n,d}]$
, ![]() $x\in\mathbb{R}^d$
, one can obtain
$x\in\mathbb{R}^d$
, one can obtain
 \begin{equation*}\frac 1 {B\left(\frac d2, \frac{n-d+1}{2}\right)} \int_{0}^{\infty} \frac{u^{d-1} \tilde f_{n,d}^* (\sigma u)}{(1+u^2)^{(n+1)/2}} {\rm d} u = b_{n,d-1}(\sigma^2) + b_{n,d-3}(\sigma^2) +\ldots\end{equation*}
\begin{equation*}\frac 1 {B\left(\frac d2, \frac{n-d+1}{2}\right)} \int_{0}^{\infty} \frac{u^{d-1} \tilde f_{n,d}^* (\sigma u)}{(1+u^2)^{(n+1)/2}} {\rm d} u = b_{n,d-1}(\sigma^2) + b_{n,d-3}(\sigma^2) +\ldots\end{equation*}
by a slight simplification of the proof of Theorem 1.6; see Remark 5.1.
2. Proof of Theorem 1.1
2.1. Reduction to intrinsic volumes
We can replace X by ![]() $-X$
because by the symmetry of the Gaussian distribution
$-X$
because by the symmetry of the Gaussian distribution
Clearly, ![]() $-\sigma X \notin \mathop{\mathrm{Conv}}\nolimits (X_1,\ldots,X_n)$
if and only if
$-\sigma X \notin \mathop{\mathrm{Conv}}\nolimits (X_1,\ldots,X_n)$
if and only if ![]() $0\notin \mathop{\mathrm{Conv}}\nolimits (X_1+\sigma X, \ldots, X_n+\sigma X)$
. This, in turn, is equivalent to the following condition:
$0\notin \mathop{\mathrm{Conv}}\nolimits (X_1+\sigma X, \ldots, X_n+\sigma X)$
. This, in turn, is equivalent to the following condition:
To interpret this geometrically, we consider the following convex cone in the space ![]() $\mathbb{R}^{n+1}$
:
$\mathbb{R}^{n+1}$
:
This cone is spanned by ![]() $e_1+\sigma e_{n+1},\ldots,e_n+\sigma e_{n+1}$
(where
$e_1+\sigma e_{n+1},\ldots,e_n+\sigma e_{n+1}$
(where ![]() $e_1,\ldots,e_{n+1}$
is the standard basis of
$e_1,\ldots,e_{n+1}$
is the standard basis of ![]() $\mathbb{R}^{n+1}$
) and is therefore isometric to the cone
$\mathbb{R}^{n+1}$
) and is therefore isometric to the cone ![]() $C_n(\sigma^2)$
introduced in (1.14). Let also U be a random linear subspace of
$C_n(\sigma^2)$
introduced in (1.14). Let also U be a random linear subspace of ![]() $\mathbb{R}^{n+1}$
given by
$\mathbb{R}^{n+1}$
given by
Observe that since ![]() $X_1,\ldots,X_n, X$
are independent, identically distributed (i.i.d.) standard Gaussian random vectors on
$X_1,\ldots,X_n, X$
are independent, identically distributed (i.i.d.) standard Gaussian random vectors on ![]() $\mathbb{R}^d$
, where
$\mathbb{R}^d$
, where ![]() $d < n$
, the linear space U almost surely (a.s.) has codimension d and is uniformly distributed on the corresponding linear Grassmannian. The above discussion shows that
$d < n$
, the linear space U almost surely (a.s.) has codimension d and is uniformly distributed on the corresponding linear Grassmannian. The above discussion shows that
The next result, known as the conic Crofton formula [28, pp. 261–262] or [4, Corollary 5.2], is of major importance for us.
Theorem 2.1. Let ![]() $C\subset \mathbb{R}^N$
be a convex polyhedral cone which is not a linear subspace. If
$C\subset \mathbb{R}^N$
be a convex polyhedral cone which is not a linear subspace. If ![]() $U\subset \mathbb{R}^N$
is a uniformly distributed linear subspace of codimension d, then
$U\subset \mathbb{R}^N$
is a uniformly distributed linear subspace of codimension d, then
where ![]() $\upsilon_0(C), \ldots, \upsilon_N(C)$
are the conic intrinsic volumes of C given by
$\upsilon_0(C), \ldots, \upsilon_N(C)$
are the conic intrinsic volumes of C given by
Combining (2.2) with the conic Crofton formula, we obtain
In the following, we shall show that the number of k-faces of ![]() $C=C_n(\sigma^2)$
is
$C=C_n(\sigma^2)$
is ![]() $\binom nk$
, and for every k-face
$\binom nk$
, and for every k-face ![]() $F\in \mathcal{F}_k(C)$
we have
$F\in \mathcal{F}_k(C)$
we have
where ![]() $g_k(r)$
is as in Section 1.2. This will prove Theorem 1.1.
$g_k(r)$
is as in Section 1.2. This will prove Theorem 1.1.
2.2. The polar cone
The polar cone of a convex cone ![]() $D\subset \mathbb{R}^N$
is defined by
$D\subset \mathbb{R}^N$
is defined by
Proposition 2.1. Let ![]() $r >-1/n$
. The polar cone of
$r >-1/n$
. The polar cone of ![]() $C_n(r)$
taken with respect to the ambient space
$C_n(r)$
taken with respect to the ambient space ![]() $L(C_n(r))$
is isometric to
$L(C_n(r))$
is isometric to ![]() $C_{n}({-}\frac{r}{1+n r})$
. That is to say, there is an orthogonal transformation
$C_{n}({-}\frac{r}{1+n r})$
. That is to say, there is an orthogonal transformation ![]() $O\,:\,\mathbb{R}^N\to\mathbb{R}^N$
such that
$O\,:\,\mathbb{R}^N\to\mathbb{R}^N$
such that
Proof. Since ![]() $D^{\circ \circ} = D$
and since the transformation
$D^{\circ \circ} = D$
and since the transformation ![]() $r\mapsto -\frac {r}{1+nr}$
is an involution, it suffices to prove the proposition for
$r\mapsto -\frac {r}{1+nr}$
is an involution, it suffices to prove the proposition for ![]() $r=\sigma^2 \geq 0$
. Since we work in the linear hull of the cone, there is no restriction of generality in assuming that it has the form
$r=\sigma^2 \geq 0$
. Since we work in the linear hull of the cone, there is no restriction of generality in assuming that it has the form ![]() $C=C_n(\sigma^2)$
given in (2.1). Thus, C is spanned by the vectors
$C=C_n(\sigma^2)$
given in (2.1). Thus, C is spanned by the vectors ![]() $u_1,\ldots,u_n$
given by
$u_1,\ldots,u_n$
given by ![]() $u_i = e_i + \sigma e_{n+1}\in \mathbb{R}^{n+1}$
,
$u_i = e_i + \sigma e_{n+1}\in \mathbb{R}^{n+1}$
, ![]() $1\leq i \leq n$
. The linear space spanned by
$1\leq i \leq n$
. The linear space spanned by ![]() $u_1,\ldots,u_n$
is
$u_1,\ldots,u_n$
is
The polar cone of ![]() $C=C_n(\sigma^2)$
taken with respect to L(C) as the ambient space is
$C=C_n(\sigma^2)$
taken with respect to L(C) as the ambient space is
The lineality space of a cone D is defined as ![]() $D\cap ({-}D)$
. The lineality space of
$D\cap ({-}D)$
. The lineality space of ![]() $C^{\circ} \cap L(C)$
is trivial, namely
$C^{\circ} \cap L(C)$
is trivial, namely
It follows that the cone ![]() $C^{\circ} \cap L(C)$
is spanned by its one-dimensional faces. These are obtained by turning all inequalities in the definition of the cone into equalities, except one. For example, one of the one-dimensional faces is given by
$C^{\circ} \cap L(C)$
is spanned by its one-dimensional faces. These are obtained by turning all inequalities in the definition of the cone into equalities, except one. For example, one of the one-dimensional faces is given by
Taking ![]() $\alpha_{n+1} = \sigma/(1+n\sigma^2)$
, we obtain that
$\alpha_{n+1} = \sigma/(1+n\sigma^2)$
, we obtain that ![]() $R_1$
is a ray spanned by the vector
$R_1$
is a ray spanned by the vector
where the value of the first coordinate was computed using the linear relation in the definition of L(C). Thus, the cone ![]() $C^{\circ}\cap L(C)$
is spanned by the vectors
$C^{\circ}\cap L(C)$
is spanned by the vectors
It is easy to verify that
 \begin{equation}\langle v_i, v_j \rangle =\begin{cases}1-\frac{\sigma^2}{1+n\sigma^2} &\text{ if } i=j,\\[8pt]
-\frac{\sigma^2}{1+n\sigma^2} &\text{ if } i\neq j.\end{cases}\end{equation}
\begin{equation}\langle v_i, v_j \rangle =\begin{cases}1-\frac{\sigma^2}{1+n\sigma^2} &\text{ if } i=j,\\[8pt]
-\frac{\sigma^2}{1+n\sigma^2} &\text{ if } i\neq j.\end{cases}\end{equation}
Thus, the cone spanned by ![]() $v_1,\ldots,v_n$
is isometric to
$v_1,\ldots,v_n$
is isometric to ![]() $C_{n}({-}\frac{\sigma^2}{1+n\sigma^2})$
.
$C_{n}({-}\frac{\sigma^2}{1+n\sigma^2})$
.
2.3. Proof of Proposition 1.1
We prove that
Consider the cone ![]() $D\subset \mathbb{R}^N$
spanned by the vectors
$D\subset \mathbb{R}^N$
spanned by the vectors ![]() $v_1,\ldots, v_n$
such that
$v_1,\ldots, v_n$
such that
 \begin{equation*}\langle v_i, v_j \rangle =\begin{cases}1-\frac{r}{1+nr} &\text{ if } i=j,\\[5pt]
-\frac{r}{1+nr} &\text{ if } i\neq j.\end{cases}\end{equation*}
\begin{equation*}\langle v_i, v_j \rangle =\begin{cases}1-\frac{r}{1+nr} &\text{ if } i=j,\\[5pt]
-\frac{r}{1+nr} &\text{ if } i\neq j.\end{cases}\end{equation*}
Then D is isometric to ![]() $C_n({-}\frac{r}{1+ nr})$
. The polar cone is given by
$C_n({-}\frac{r}{1+ nr})$
. The polar cone is given by
Let ![]() $\xi$
be a standard normal random vector on
$\xi$
be a standard normal random vector on ![]() $\mathbb{R}^{N}$
. Then the solid angle of
$\mathbb{R}^{N}$
. Then the solid angle of ![]() $D^{\circ}$
is given by
$D^{\circ}$
is given by
Introducing the random variables ![]() $\eta_i \coloneqq \langle \xi,v_i\rangle$
,
$\eta_i \coloneqq \langle \xi,v_i\rangle$
, ![]() $i=1,\ldots,n$
, we observe that the random vector
$i=1,\ldots,n$
, we observe that the random vector ![]() $(\eta_1,\ldots,\eta_n)$
is zero-mean Gaussian with covariances given by
$(\eta_1,\ldots,\eta_n)$
is zero-mean Gaussian with covariances given by
 \begin{equation}\mathop{\mathrm{Cov}}\nolimits (\eta_i, \eta_j)=\langle v_i, v_j\rangle=\begin{cases}1-\frac{r}{1+nr} &\text{ if } i=j,\\[5pt]
-\frac{r}{1+nr} &\text{ if } i\neq j.\end{cases}\end{equation}
\begin{equation}\mathop{\mathrm{Cov}}\nolimits (\eta_i, \eta_j)=\langle v_i, v_j\rangle=\begin{cases}1-\frac{r}{1+nr} &\text{ if } i=j,\\[5pt]
-\frac{r}{1+nr} &\text{ if } i\neq j.\end{cases}\end{equation}
Hence, ![]() $\alpha(D^{\circ}) = \mathbb{P}[\eta_1\leq 0,\ldots,\eta_n \leq 0] = g_n\left({-}\frac{r}{1+ n r}\right)$
by definition of
$\alpha(D^{\circ}) = \mathbb{P}[\eta_1\leq 0,\ldots,\eta_n \leq 0] = g_n\left({-}\frac{r}{1+ n r}\right)$
by definition of ![]() $g_n$
. On the other hand,
$g_n$
. On the other hand, ![]() $D^{\circ}$
is the direct sum of
$D^{\circ}$
is the direct sum of ![]() $L(D)\cap D^{\circ}$
and the orthogonal complement of L(D). It follows that
$L(D)\cap D^{\circ}$
and the orthogonal complement of L(D). It follows that
By Proposition 2.1, ![]() $L(D)\cap D^{\circ}$
is isometric to
$L(D)\cap D^{\circ}$
is isometric to ![]() $C_n(r)$
, thus completing the proof.
$C_n(r)$
, thus completing the proof.
2.4. Internal and normal angles: proof of (2.4)
Recall that C is a cone given by (2.1) and that the linear hull of C is a codimension-1 linear subspace of ![]() $\mathbb{R}^n$
given by
$\mathbb{R}^n$
given by
Inside L(C), the convex cone C is defined by the inequalities ![]() $\alpha_1\geq 0,\ldots,\alpha_n\geq 0$
. The k-faces of C are obtained by turning
$\alpha_1\geq 0,\ldots,\alpha_n\geq 0$
. The k-faces of C are obtained by turning ![]() $n-k$
of these inequalities into equalities; therefore the number of k-faces is
$n-k$
of these inequalities into equalities; therefore the number of k-faces is ![]() $\binom nk$
. Without restriction of generality, we consider a k-face F of the form
$\binom nk$
. Without restriction of generality, we consider a k-face F of the form
Since F is isometric to ![]() $C_k(\sigma^2)$
, Proposition 1.1 yields the following formula for its solid angle:
$C_k(\sigma^2)$
, Proposition 1.1 yields the following formula for its solid angle:
To compute ![]() $\alpha(N_F(C))$
, observe that by the polar correspondence,
$\alpha(N_F(C))$
, observe that by the polar correspondence, ![]() $N_F(C)\cap L(C)$
is some
$N_F(C)\cap L(C)$
is some ![]() $(n-k)$
-dimensional face of the polar cone
$(n-k)$
-dimensional face of the polar cone ![]() $C^{\circ}\cap L(C)$
. The latter cone is isometric to
$C^{\circ}\cap L(C)$
. The latter cone is isometric to ![]() $C_{n}({-}\frac{\sigma^2}{1+n\sigma^2})$
by Proposition 2.1. Since all
$C_{n}({-}\frac{\sigma^2}{1+n\sigma^2})$
by Proposition 2.1. Since all ![]() $(n-k)$
-dimensional faces of
$(n-k)$
-dimensional faces of ![]() $C_{n}({-}\frac{\sigma^2}{1+n\sigma^2})$
are isometric to
$C_{n}({-}\frac{\sigma^2}{1+n\sigma^2})$
are isometric to ![]() $C_{n-k}({-}\frac{\sigma^2}{1+n\sigma^2})$
, we can apply Proposition 1.1 to obtain that
$C_{n-k}({-}\frac{\sigma^2}{1+n\sigma^2})$
, we can apply Proposition 1.1 to obtain that
 \begin{align*}\alpha(N_F(C)) = \alpha(N_F(C)\cap L(C)) & = \alpha\left(C_{n-k}\left({-}\frac{\sigma^2}{1+n\sigma^2}\right)\right)\\[5pt]
& = g_{n-k}\left({-} \frac{-\frac{\sigma^2}{1+n\sigma^2}}{1- \frac{(n-k)\sigma^2}{1+n\sigma^2}} \right)=g_{n-k} \left(\frac{\sigma^2}{1+k\sigma^2}\right).\end{align*}
\begin{align*}\alpha(N_F(C)) = \alpha(N_F(C)\cap L(C)) & = \alpha\left(C_{n-k}\left({-}\frac{\sigma^2}{1+n\sigma^2}\right)\right)\\[5pt]
& = g_{n-k}\left({-} \frac{-\frac{\sigma^2}{1+n\sigma^2}}{1- \frac{(n-k)\sigma^2}{1+n\sigma^2}} \right)=g_{n-k} \left(\frac{\sigma^2}{1+k\sigma^2}\right).\end{align*}
2.5. Proof of Proposition 1.2
By symmetry, we may consider the face of the form ![]() $F= \mathop{\mathrm{Conv}}\nolimits(e_1,\ldots,e_{k})$
. It follows from (1.17) that the tangent cone is given by
$F= \mathop{\mathrm{Conv}}\nolimits(e_1,\ldots,e_{k})$
. It follows from (1.17) that the tangent cone is given by
Thus, ![]() $T_F(\Delta_n)$
is a direct orthogonal sum of the linear subspace
$T_F(\Delta_n)$
is a direct orthogonal sum of the linear subspace ![]() $L_{n,k}$
given by
$L_{n,k}$
given by ![]() $\alpha_1+\ldots+\alpha_k=0$
,
$\alpha_1+\ldots+\alpha_k=0$
, ![]() $\alpha_{k+1}=\ldots=\alpha_n = 0$
(which is the lineality space of the cone) and the cone
$\alpha_{k+1}=\ldots=\alpha_n = 0$
(which is the lineality space of the cone) and the cone ![]() $D_{n,k} = \mathop{\mathrm{pos}}\nolimits (u_1,\ldots,u_{n-k})$
spanned by the
$D_{n,k} = \mathop{\mathrm{pos}}\nolimits (u_1,\ldots,u_{n-k})$
spanned by the ![]() $n-k$
vectors
$n-k$
vectors
The scalar products of these vectors are given by
 \begin{equation*}\langle u_i, u_j\rangle=\begin{cases}1+\frac 1k &\text{ if } i=j,\\[5pt]
\frac 1k &\text{ if } i\neq j.\end{cases}\end{equation*}
\begin{equation*}\langle u_i, u_j\rangle=\begin{cases}1+\frac 1k &\text{ if } i=j,\\[5pt]
\frac 1k &\text{ if } i\neq j.\end{cases}\end{equation*}
Hence, the cone ![]() $D_{n,k}$
is isometric to
$D_{n,k}$
is isometric to ![]() $C_{n-k}(1/k)$
. From Proposition 1.1 we deduce that the solid angle of
$C_{n-k}(1/k)$
. From Proposition 1.1 we deduce that the solid angle of ![]() $T_F(\Delta_n)$
is
$T_F(\Delta_n)$
is ![]() $g_{n-k}({-}1/n)$
.
$g_{n-k}({-}1/n)$
.
The normal cone ![]() $N_F(\Delta_n)= T_F^\circ(\Delta_n)$
is the direct orthogonal sum of the line
$N_F(\Delta_n)= T_F^\circ(\Delta_n)$
is the direct orthogonal sum of the line ![]() $\{\alpha_1=\ldots=\alpha_n\}$
and the polar cone of
$\{\alpha_1=\ldots=\alpha_n\}$
and the polar cone of ![]() $D_{n,k}$
taken with respect to the ambient space
$D_{n,k}$
taken with respect to the ambient space ![]() $L(D_{n,k})$
. The latter cone is isometric to
$L(D_{n,k})$
. The latter cone is isometric to ![]() $C_{n-k}({-}1/n)$
by Proposition 2.1. From Proposition 1.1 we deduce that the solid angle of
$C_{n-k}({-}1/n)$
by Proposition 2.1. From Proposition 1.1 we deduce that the solid angle of ![]() $N_F(\Delta_n)$
equals
$N_F(\Delta_n)$
equals ![]() $g_{n-k}(1/k)$
.
$g_{n-k}(1/k)$
.
2.6. Proof of Proposition 1.3
If ![]() $r= \sigma^2\geq 0$
, then the proof follows immediately from (2.4). Let
$r= \sigma^2\geq 0$
, then the proof follows immediately from (2.4). Let ![]() $r\in ({-}\frac 1n, 0)$
. For a cone
$r\in ({-}\frac 1n, 0)$
. For a cone ![]() $D\subset \mathbb{R}^N$
we have the relation
$D\subset \mathbb{R}^N$
we have the relation ![]() $\upsilon_k(D) = \upsilon_{N-k}(D^\circ)$
; see [4, Section 2.2]. Applying this relation to the cone
$\upsilon_k(D) = \upsilon_{N-k}(D^\circ)$
; see [4, Section 2.2]. Applying this relation to the cone ![]() $C_n(r)$
in the ambient space
$C_n(r)$
in the ambient space ![]() $L(C_n(r))$
and recalling Proposition 2.1, we obtain
$L(C_n(r))$
and recalling Proposition 2.1, we obtain
where the last step follows from the already established part of Proposition 1.3 and the fact that ![]() $-\frac{r}{1+nr}>0$
. Using the definition of
$-\frac{r}{1+nr}>0$
. Using the definition of ![]() $b_{n,n-k}$
, we obtain
$b_{n,n-k}$
, we obtain
 \begin{align*} & b_{n,n-k}\left({-}\frac{r}{1+nr}\right)=\binom {n}{n-k}g_{n-k}\left({-} \frac{-\frac{r}{1+nr}}{1-\frac{(n-k)r}{1+nr}}\right) g_k \left(\frac{-\frac{r}{1+nr}}{1 - \frac{(n-k)r}{1+nr}}\right)\\[4pt]
& \quad =\binom {n}{k}g_k \left({-}\frac{r}{1+kr}\right) g_{n-k}\left(\frac{r}{1+kr}\right)=b_{n,k}(r),\end{align*}
\begin{align*} & b_{n,n-k}\left({-}\frac{r}{1+nr}\right)=\binom {n}{n-k}g_{n-k}\left({-} \frac{-\frac{r}{1+nr}}{1-\frac{(n-k)r}{1+nr}}\right) g_k \left(\frac{-\frac{r}{1+nr}}{1 - \frac{(n-k)r}{1+nr}}\right)\\[4pt]
& \quad =\binom {n}{k}g_k \left({-}\frac{r}{1+kr}\right) g_{n-k}\left(\frac{r}{1+kr}\right)=b_{n,k}(r),\end{align*}
which proves the claimed formula.
3. Properties of  ${\mathbf{g}}_{\mathbf{n}}$
${\mathbf{g}}_{\mathbf{n}}$
3.1. Proof of Proposition 1.4
In the following let ![]() $(\eta_1,\ldots,\eta_n)$
be a zero-mean Gaussian vector whose covariance matrix
$(\eta_1,\ldots,\eta_n)$
be a zero-mean Gaussian vector whose covariance matrix ![]() $\Sigma = (r_{ij})_{i,j=1}^n$
is given by
$\Sigma = (r_{ij})_{i,j=1}^n$
is given by
 \begin{equation*}r_{ij} = \mathop{\mathrm{Cov}}\nolimits (\eta_i,\eta_j) =\begin{cases}1+r &\text{ if } i=j,\\[5pt]
r &\text{ if } i\neq j.\end{cases}\end{equation*}
\begin{equation*}r_{ij} = \mathop{\mathrm{Cov}}\nolimits (\eta_i,\eta_j) =\begin{cases}1+r &\text{ if } i=j,\\[5pt]
r &\text{ if } i\neq j.\end{cases}\end{equation*}
Using the inequality between the arithmetic and quadratic means, it is easy to check that this matrix is positive semidefinite for ![]() $r\geq -1/n$
. Recall that by definition
$r\geq -1/n$
. Recall that by definition
Proof of (a). Let ![]() $r>-1/n$
be real. (The case
$r>-1/n$
be real. (The case ![]() $r=-1/n$
can be then deduced from the continuity of
$r=-1/n$
can be then deduced from the continuity of ![]() $g_n$
at
$g_n$
at ![]() $-1/n$
.) It is straightforward to check that
$-1/n$
.) It is straightforward to check that ![]() $\det \Sigma = 1+rn>0$
and that the inverse matrix
$\det \Sigma = 1+rn>0$
and that the inverse matrix ![]() $\Sigma^{-1} = (s_{ij})_{i,j=1}^n$
is given by
$\Sigma^{-1} = (s_{ij})_{i,j=1}^n$
is given by
 \begin{equation*}s_{ij} =\begin{cases}1 - \frac{r}{1+nr} &\text{ if } i=j,\\[5pt]
- \frac{r}{1+nr} &\text{ if } i\neq j.\end{cases}\end{equation*}
\begin{equation*}s_{ij} =\begin{cases}1 - \frac{r}{1+nr} &\text{ if } i=j,\\[5pt]
- \frac{r}{1+nr} &\text{ if } i\neq j.\end{cases}\end{equation*}
Using (3.1) and the formula for the multivariate Gaussian density, we obtain, for all ![]() $r>-1/n$
,
$r>-1/n$
,
 \begin{align}g_n(r) = \frac{1}{(2\pi)^{n/2} \sqrt{1+nr}} \int_{(0,\infty)^n}\exp\left\{ \frac{r}{2(1+nr)} \left(\sum_{j=1}^n x_j\right)^2 - \frac 12\sum_{j=1}^n x_j^2\right\} {\rm d} x_1 \ldots {\rm d} x_n.\nonumber\\
\end{align}
\begin{align}g_n(r) = \frac{1}{(2\pi)^{n/2} \sqrt{1+nr}} \int_{(0,\infty)^n}\exp\left\{ \frac{r}{2(1+nr)} \left(\sum_{j=1}^n x_j\right)^2 - \frac 12\sum_{j=1}^n x_j^2\right\} {\rm d} x_1 \ldots {\rm d} x_n.\nonumber\\
\end{align}
The integral converges for complex r satisfying ![]() $\operatorname{Re} \frac{r}{1+nr} <\frac 1n$
, which is equivalent to
$\operatorname{Re} \frac{r}{1+nr} <\frac 1n$
, which is equivalent to ![]() $\operatorname{Re} r > -\frac 1n$
. Indeed, by the inequality
$\operatorname{Re} r > -\frac 1n$
. Indeed, by the inequality ![]() $(\!\sum_{j=1}^n x_j)^2 \leq n \sum_{j=1}^n x_j^2$
, we have
$(\!\sum_{j=1}^n x_j)^2 \leq n \sum_{j=1}^n x_j^2$
, we have
 \begin{equation*}\operatorname{Re} \left(\frac{r}{2(1+nr)} \left(\sum_{j=1}^n x_j\right)^2 - \frac 12\sum_{j=1}^n x_j^2 \right)\leq\frac 12 \left(\operatorname{Re}\frac{r}{(1+nr)} - \frac 1n\right) \left(\sum_{j=1}^n x_j\right)^2.\end{equation*}
\begin{equation*}\operatorname{Re} \left(\frac{r}{2(1+nr)} \left(\sum_{j=1}^n x_j\right)^2 - \frac 12\sum_{j=1}^n x_j^2 \right)\leq\frac 12 \left(\operatorname{Re}\frac{r}{(1+nr)} - \frac 1n\right) \left(\sum_{j=1}^n x_j\right)^2.\end{equation*}
Hence the right-hand side of (3.2) defines an analytic function of r in the half-plane ![]() $\operatorname{Re} r > -\frac 1n$
. In particular,
$\operatorname{Re} r > -\frac 1n$
. In particular, ![]() $g_n(r)$
has an analytic continuation to this half-plane.
$g_n(r)$
has an analytic continuation to this half-plane.
Next we prove that for all ![]() $r>0$
,
$r>0$
,
Let ![]() $\xi,\xi_1,\ldots,\xi_n$
be i.i.d. standard Gaussian random variables. We have a distributional representation
$\xi,\xi_1,\ldots,\xi_n$
be i.i.d. standard Gaussian random variables. We have a distributional representation ![]() $\eta_ k= \xi_k - \sqrt r\xi$
,
$\eta_ k= \xi_k - \sqrt r\xi$
, ![]() $k=1,\ldots,n$
. It follows that
$k=1,\ldots,n$
. It follows that
 \begin{align}g_n(r)&=\mathbb{P}[\eta_1<0,\ldots,\eta_n <0]\notag\\[5pt]
&=\mathbb{P}[\xi_1 < \sqrt r \xi, \ldots, \xi_n
< \sqrt r \xi]\notag\\[5pt]
&=\frac 1 {\sqrt{2\pi}} \int_{-\infty}^{+\infty} \Phi^{n}(\sqrt r x) {\rm e}^{-x^2/2} {\rm d} x,\end{align}
\begin{align}g_n(r)&=\mathbb{P}[\eta_1<0,\ldots,\eta_n <0]\notag\\[5pt]
&=\mathbb{P}[\xi_1 < \sqrt r \xi, \ldots, \xi_n
< \sqrt r \xi]\notag\\[5pt]
&=\frac 1 {\sqrt{2\pi}} \int_{-\infty}^{+\infty} \Phi^{n}(\sqrt r x) {\rm e}^{-x^2/2} {\rm d} x,\end{align}
which yields (3.3) after splitting the integral.
It remains to prove that the right-hand side of (3.3) is an analytic function of r in the half-plane ![]() $\operatorname{Re} r > -\frac 1n$
, which would imply that (3.3) holds in this half-plane by the uniqueness of the analytic continuation. First of all, observe that for every fixed
$\operatorname{Re} r > -\frac 1n$
, which would imply that (3.3) holds in this half-plane by the uniqueness of the analytic continuation. First of all, observe that for every fixed ![]() $x>0$
, the expression
$x>0$
, the expression ![]() $\Phi^n(z x) + \Phi^n({-} z x)$
is an analytic function of
$\Phi^n(z x) + \Phi^n({-} z x)$
is an analytic function of ![]() $z\in \mathbb{C}$
which remains invariant under the substitution
$z\in \mathbb{C}$
which remains invariant under the substitution ![]() $z\mapsto -z$
. Hence it can be written as an everywhere convergent Taylor series in even powers of z. It follows that for every fixed
$z\mapsto -z$
. Hence it can be written as an everywhere convergent Taylor series in even powers of z. It follows that for every fixed ![]() $x>0$
, the expression
$x>0$
, the expression ![]() $(\Phi^n(\sqrt r x) + \Phi^n({-}\sqrt r x))$
defines an analytic function of
$(\Phi^n(\sqrt r x) + \Phi^n({-}\sqrt r x))$
defines an analytic function of ![]() $r\in\mathbb{C}$
. To prove the analyticity of the integral on the right-hand side of (3.3), we argue as follows. We have the estimate
$r\in\mathbb{C}$
. To prove the analyticity of the integral on the right-hand side of (3.3), we argue as follows. We have the estimate
It follows that
By the dominated convergence theorem, the right-hand side of (3.3) is a continuous function of r on the half-plane ![]() $\operatorname{Re} r > -\frac 1n$
. Moreover, by Fubini’s theorem and by the analyticity of
$\operatorname{Re} r > -\frac 1n$
. Moreover, by Fubini’s theorem and by the analyticity of ![]() $(\Phi^n(\sqrt r x) + \Phi^n({-}\sqrt r x))$
, the integral of the right-hand side of (3.3) along any triangular contour vanishes. By Morera’s theorem, the right-hand side of (3.3) is an analytic function in the half-plane
$(\Phi^n(\sqrt r x) + \Phi^n({-}\sqrt r x))$
, the integral of the right-hand side of (3.3) along any triangular contour vanishes. By Morera’s theorem, the right-hand side of (3.3) is an analytic function in the half-plane ![]() $\operatorname{Re} r > -\frac 1n$
. By the uniqueness principle for analytic functions, (3.3) must hold in this half-plane.
$\operatorname{Re} r > -\frac 1n$
. By the uniqueness principle for analytic functions, (3.3) must hold in this half-plane.
Proof of (b). By analyticity, it suffices to consider ![]() $r>0$
. Differentiating under the sign of the integral in (3.4), we obtain
$r>0$
. Differentiating under the sign of the integral in (3.4), we obtain
 \begin{align*}g^{\prime}_n(r)&=\frac 1{\sqrt{2\pi}} \int_{-\infty}^{+\infty} n \Phi^{n-1}(\sqrt r x) \frac 1 {\sqrt{2\pi}} {\rm e}^{-rx^2/2} \frac x {2\sqrt r} {\rm e}^{-x^2/2} {\rm d} x\\[8pt]
&=\frac n {4\pi\sqrt r} \int_{-\infty}^{+\infty} \Phi^{n-1}(\sqrt r x) x {\rm e}^{-(r+1)x^2/2} {\rm d} x.\end{align*}
\begin{align*}g^{\prime}_n(r)&=\frac 1{\sqrt{2\pi}} \int_{-\infty}^{+\infty} n \Phi^{n-1}(\sqrt r x) \frac 1 {\sqrt{2\pi}} {\rm e}^{-rx^2/2} \frac x {2\sqrt r} {\rm e}^{-x^2/2} {\rm d} x\\[8pt]
&=\frac n {4\pi\sqrt r} \int_{-\infty}^{+\infty} \Phi^{n-1}(\sqrt r x) x {\rm e}^{-(r+1)x^2/2} {\rm d} x.\end{align*}
Writing ![]() $x {\rm e}^{-(r+1)x^2/2}{\rm d} x = -\frac 1 {r+1} {\rm d} {\rm e}^{-(r+1)x^2/2}$
and integrating by parts yields
$x {\rm e}^{-(r+1)x^2/2}{\rm d} x = -\frac 1 {r+1} {\rm d} {\rm e}^{-(r+1)x^2/2}$
and integrating by parts yields
 \begin{align*}g^{\prime}_n (r)&=\frac n {4\pi\sqrt r} \int_{-\infty}^{+\infty} (n-1) \Phi^{n-2}(\sqrt r x) \frac 1 {\sqrt{2\pi}} {\rm e}^{-rx^2/2} \sqrt r \cdot \frac 1 {r+1}{\rm e}^{-(r+1)x^2/2} {\rm d} x\\[8pt]
&=\frac {n(n-1)} {4\pi (r+1)} \frac 1 {\sqrt{2\pi}} \int_{-\infty}^{+\infty} \Phi^{n-2}(\sqrt r x) {\rm e}^{-(2r+1)x^2/2} {\rm d} x.\end{align*}
\begin{align*}g^{\prime}_n (r)&=\frac n {4\pi\sqrt r} \int_{-\infty}^{+\infty} (n-1) \Phi^{n-2}(\sqrt r x) \frac 1 {\sqrt{2\pi}} {\rm e}^{-rx^2/2} \sqrt r \cdot \frac 1 {r+1}{\rm e}^{-(r+1)x^2/2} {\rm d} x\\[8pt]
&=\frac {n(n-1)} {4\pi (r+1)} \frac 1 {\sqrt{2\pi}} \int_{-\infty}^{+\infty} \Phi^{n-2}(\sqrt r x) {\rm e}^{-(2r+1)x^2/2} {\rm d} x.\end{align*}
Finally, making the change of variables ![]() $y\coloneqq \sqrt{2r+1}\, x$
, we arrive at
$y\coloneqq \sqrt{2r+1}\, x$
, we arrive at
 \begin{align*}g^{\prime}_n(r)&= \frac {n(n-1)} {4\pi (r+1)\sqrt{2r+1}} \frac 1 {\sqrt{2\pi}} \int_{-\infty}^{+\infty} \Phi^{n-2}\left(\sqrt {\frac {r}{2r+1}} \, y\right){\rm e}^{-y^2/2} {\rm d} y\\[5pt]
&=\frac {n(n-1)} {4\pi (r+1)\sqrt{2r+1}} g_{n-2}\left(\frac {r}{2r+1}\right).\end{align*}
\begin{align*}g^{\prime}_n(r)&= \frac {n(n-1)} {4\pi (r+1)\sqrt{2r+1}} \frac 1 {\sqrt{2\pi}} \int_{-\infty}^{+\infty} \Phi^{n-2}\left(\sqrt {\frac {r}{2r+1}} \, y\right){\rm e}^{-y^2/2} {\rm d} y\\[5pt]
&=\frac {n(n-1)} {4\pi (r+1)\sqrt{2r+1}} g_{n-2}\left(\frac {r}{2r+1}\right).\end{align*}
Proof of (c). By definition, ![]() $g_1(r) = \mathbb{P}[\eta_1 <0] = \frac 12$
, since
$g_1(r) = \mathbb{P}[\eta_1 <0] = \frac 12$
, since ![]() $\eta_1$
is centered Gaussian.
$\eta_1$
is centered Gaussian.
Proof of (d) and (e). In the case ![]() $r=0$
, the random variables
$r=0$
, the random variables ![]() $\eta_1,\ldots,\eta_n$
are independent standard Gaussian and hence
$\eta_1,\ldots,\eta_n$
are independent standard Gaussian and hence
In the case ![]() $r=1$
, we have a distributional representation
$r=1$
, we have a distributional representation ![]() $\eta_i = \xi_i - \xi$
, where
$\eta_i = \xi_i - \xi$
, where ![]() $\xi,\xi_1,\ldots,\xi_n$
are independent standard Gaussian. Hence
$\xi,\xi_1,\ldots,\xi_n$
are independent standard Gaussian. Hence
because any of the values ![]() $\xi,\xi_1,\ldots,\xi_n$
can be the maximum with the same probability.
$\xi,\xi_1,\ldots,\xi_n$
can be the maximum with the same probability.
To prove that ![]() $\lim_{r\to +\infty} g_n(r) = \frac 12$
, use (3.3) together with the relation
$\lim_{r\to +\infty} g_n(r) = \frac 12$
, use (3.3) together with the relation
and the dominated convergence theorem.
Finally, in the case ![]() $r=-1/n$
we have the linear relation
$r=-1/n$
we have the linear relation ![]() $\eta_1+\ldots+\eta_n = 0$
(which can be verified by showing that the variance of
$\eta_1+\ldots+\eta_n = 0$
(which can be verified by showing that the variance of ![]() $\eta_1+\ldots+\eta_n$
vanishes); hence
$\eta_1+\ldots+\eta_n$
vanishes); hence ![]() $g_n({-}\frac 1n) = 0$
.
$g_n({-}\frac 1n) = 0$
.
Proof of (f). Let ![]() $n=2$
. Introduce the variables
$n=2$
. Introduce the variables ![]() $\eta_1^*\coloneqq \eta_1/\sqrt{r+1}$
and
$\eta_1^*\coloneqq \eta_1/\sqrt{r+1}$
and ![]() $\eta_2^* \coloneqq \eta_2 /\sqrt{r+1}$
which have joint Gaussian law with unit variances and covariance
$\eta_2^* \coloneqq \eta_2 /\sqrt{r+1}$
which have joint Gaussian law with unit variances and covariance ![]() $r/(1+r)$
. It follows that
$r/(1+r)$
. It follows that
by the well-known Sheppard formula for the quadrant probability of a bivariate Gaussian density; see [7, p. 121] and the references therein.
An alternative proof of this identity is based on Part (b). We give only the proof for ![]() $g_3$
, since the proof for
$g_3$
, since the proof for ![]() $g_2$
is similar. By Part (b),
$g_2$
is similar. By Part (b), ![]() $g_3$
satisfies the differential equation
$g_3$
satisfies the differential equation ![]() $g^{\prime}_3(r) = \frac 3 {4\pi} \frac{1}{(r+1)\sqrt{2r+1}}$
together with the initial condition
$g^{\prime}_3(r) = \frac 3 {4\pi} \frac{1}{(r+1)\sqrt{2r+1}}$
together with the initial condition ![]() $g_3(0)= 1/8$
. It is easy to check that
$g_3(0)= 1/8$
. It is easy to check that ![]() $g_3(r) = \frac 18 + \frac 3 {4\pi} \arcsin \frac{r}{1+r}$
is the solution.
$g_3(r) = \frac 18 + \frac 3 {4\pi} \arcsin \frac{r}{1+r}$
is the solution.
Proof of (g). Using (3.2) with ![]() $r = -\frac 1n + \varepsilon$
and then introducing the variables
$r = -\frac 1n + \varepsilon$
and then introducing the variables ![]() $y_i \coloneqq x_i / \sqrt \varepsilon$
yields
$y_i \coloneqq x_i / \sqrt \varepsilon$
yields
 \begin{align*}g_n\left({-}\frac 1n + \varepsilon\right)&= \frac 1 {(2\pi)^{n/2} \sqrt{n\varepsilon}} \int_{(0,\infty)^n} \exp\left\{ \frac {-\frac 1n + \varepsilon}{2\varepsilon n} \left(\sum_{i=1}^n x_i\right)^2 - \frac 12 \sum_{i=1}^n x_i^2 \right\} {\rm d} x_1\ldots {\rm d} x_n\\[5pt]
&= \frac {\varepsilon^{n/2}} {(2\pi)^{n/2} \sqrt{n\varepsilon}}\int_{(0,\infty)^n} \exp\left\{ \frac {-\frac 1n + \varepsilon}{2n} \left(\sum_{i=1}^n y_i\right)^2 - \frac \varepsilon 2 \sum_{i=1}^n y_i^2 \right\} {\rm d} y_1\ldots {\rm d} y_n\\[5pt]
&\sim \frac {\varepsilon^{(n-1)/2}} {(2\pi)^{n/2} \sqrt{n}} \int_{(0,\infty)^n} \exp\left\{ -\frac {1}{2n^2} \left(\sum_{i=1}^n y_i\right)^2\right\} {\rm d} y_1\ldots {\rm d} y_n\end{align*}
\begin{align*}g_n\left({-}\frac 1n + \varepsilon\right)&= \frac 1 {(2\pi)^{n/2} \sqrt{n\varepsilon}} \int_{(0,\infty)^n} \exp\left\{ \frac {-\frac 1n + \varepsilon}{2\varepsilon n} \left(\sum_{i=1}^n x_i\right)^2 - \frac 12 \sum_{i=1}^n x_i^2 \right\} {\rm d} x_1\ldots {\rm d} x_n\\[5pt]
&= \frac {\varepsilon^{n/2}} {(2\pi)^{n/2} \sqrt{n\varepsilon}}\int_{(0,\infty)^n} \exp\left\{ \frac {-\frac 1n + \varepsilon}{2n} \left(\sum_{i=1}^n y_i\right)^2 - \frac \varepsilon 2 \sum_{i=1}^n y_i^2 \right\} {\rm d} y_1\ldots {\rm d} y_n\\[5pt]
&\sim \frac {\varepsilon^{(n-1)/2}} {(2\pi)^{n/2} \sqrt{n}} \int_{(0,\infty)^n} \exp\left\{ -\frac {1}{2n^2} \left(\sum_{i=1}^n y_i\right)^2\right\} {\rm d} y_1\ldots {\rm d} y_n\end{align*}
as ![]() $\varepsilon \downarrow 0$
. The volume of the simplex
$\varepsilon \downarrow 0$
. The volume of the simplex ![]() $\{y_1,\ldots,y_n\geq 0, y_1+\ldots+ y_n\leq s\}$
is
$\{y_1,\ldots,y_n\geq 0, y_1+\ldots+ y_n\leq s\}$
is ![]() $s^n/n!$
. Hence the integral on the right-hand side equals
$s^n/n!$
. Hence the integral on the right-hand side equals
which completes the proof of (g).
Proof of (h). The functions ![]() $g_0(r)=1$
and
$g_0(r)=1$
and ![]() $g_1(r) = 1/2$
are defined on the whole complex plane. Assume, by induction, that
$g_1(r) = 1/2$
are defined on the whole complex plane. Assume, by induction, that ![]() $g_{2n-2}$
and
$g_{2n-2}$
and ![]() $g_{2n-1}$
are defined as multivalued analytic functions everywhere outside the set
$g_{2n-1}$
are defined as multivalued analytic functions everywhere outside the set ![]() $\{-1/k\colon k=1,\ldots, 2n-2\}$
. In order to define
$\{-1/k\colon k=1,\ldots, 2n-2\}$
. In order to define ![]() $g_{2n}$
and
$g_{2n}$
and ![]() $g_{2n+1}$
we use the differential equations from Part (b):
$g_{2n+1}$
we use the differential equations from Part (b):
 \begin{align*}g^{\prime}_{2n}(r)&= \frac{n(2n-1)}{2\pi (r+1)\sqrt{2r+1}} g_{2n-2} \left(\frac{r}{2r+1}\right),\\[6pt]
g^{\prime}_{2n+1}(r)&=\frac{n(2n+1)}{2\pi (r+1)\sqrt{2r+1}} g_{2n-1} \left(\frac{r}{2r+1}\right).\end{align*}
\begin{align*}g^{\prime}_{2n}(r)&= \frac{n(2n-1)}{2\pi (r+1)\sqrt{2r+1}} g_{2n-2} \left(\frac{r}{2r+1}\right),\\[6pt]
g^{\prime}_{2n+1}(r)&=\frac{n(2n+1)}{2\pi (r+1)\sqrt{2r+1}} g_{2n-1} \left(\frac{r}{2r+1}\right).\end{align*}
It is easy to check that ![]() $\frac{r}{2r+1} \in \{-1/k\colon k=1,\ldots, 2n-2\}$
if and only if
$\frac{r}{2r+1} \in \{-1/k\colon k=1,\ldots, 2n-2\}$
if and only if ![]() $r\in \{-\frac 13, -\frac 14, \ldots,\break -\frac 1 {2n}\}$
. Hence the right-hand sides of the differential equations are defined as analytic functions on some unramified cover of
$r\in \{-\frac 13, -\frac 14, \ldots,\break -\frac 1 {2n}\}$
. Hence the right-hand sides of the differential equations are defined as analytic functions on some unramified cover of ![]() $\mathbb{C}\backslash \{-1/k\colon k=1,\ldots, 2n\}$
, and we can define
$\mathbb{C}\backslash \{-1/k\colon k=1,\ldots, 2n\}$
, and we can define ![]() $g_{2n}$
and
$g_{2n}$
and ![]() $g_{2n+1}$
by path integration.
$g_{2n+1}$
by path integration.
3.2. Proof of Proposition 1.5
For ![]() $m\in \mathbb{N}_0$
and
$m\in \mathbb{N}_0$
and ![]() $n=m+2,m+3,\ldots$
write
$n=m+2,m+3,\ldots$
write
We have to show that ![]() $I(m,n)= 0$
. From (1.20) we already know that
$I(m,n)= 0$
. From (1.20) we already know that ![]() $I(0,n) = 0$
for all
$I(0,n) = 0$
for all ![]() $n=2,3,\ldots$
, which is the basis of our induction. Define also
$n=2,3,\ldots$
, which is the basis of our induction. Define also ![]() $I({-}1,n) = 0$
for
$I({-}1,n) = 0$
for ![]() $n\in\mathbb{N}$
. It follows from (1.6) that
$n\in\mathbb{N}$
. It follows from (1.6) that
Performing partial integration, we can write
 \begin{align*}I(m,n)&=-\frac{i \sqrt{2\pi}}{n+1} \int_{-\infty}^{+\infty} y^m {\rm e}^{-(n+1) y^2/2} {\rm d} \Phi^{n+1}(iy)\\[7pt]
&=\frac{i \sqrt{2\pi}}{n+1} \int_{-\infty}^{+\infty} \Phi^{n+1}(iy) \left(m y^{m-1}{\rm e}^{-(n+1) y^2/2} - (n+1) y^{m+1} {\rm e}^{-(n+1) y^2/2}\right) {\rm d} y\\[7pt]
&=\frac{i \sqrt{2\pi}}{n+1} \left(m I(m-1,n+1) - (n+1)I(m+1,n+1)\right).\end{align*}
\begin{align*}I(m,n)&=-\frac{i \sqrt{2\pi}}{n+1} \int_{-\infty}^{+\infty} y^m {\rm e}^{-(n+1) y^2/2} {\rm d} \Phi^{n+1}(iy)\\[7pt]
&=\frac{i \sqrt{2\pi}}{n+1} \int_{-\infty}^{+\infty} \Phi^{n+1}(iy) \left(m y^{m-1}{\rm e}^{-(n+1) y^2/2} - (n+1) y^{m+1} {\rm e}^{-(n+1) y^2/2}\right) {\rm d} y\\[7pt]
&=\frac{i \sqrt{2\pi}}{n+1} \left(m I(m-1,n+1) - (n+1)I(m+1,n+1)\right).\end{align*}
Observe that this identity is true also for ![]() $m=0$
. Assuming by induction that we proved that
$m=0$
. Assuming by induction that we proved that ![]() $I(l,n) = 0$
for all
$I(l,n) = 0$
for all ![]() $l=0,1,\ldots,m$
and
$l=0,1,\ldots,m$
and ![]() $n=l+2,l+3,\ldots$
, we obtain from the above identity that
$n=l+2,l+3,\ldots$
, we obtain from the above identity that ![]() $I(m+1,n+1) = 0$
.
$I(m+1,n+1) = 0$
.
Let now ![]() $n= m+1$
, in which case the integral diverges and we have to pass to the Cauchy principal value. Write
$n= m+1$
, in which case the integral diverges and we have to pass to the Cauchy principal value. Write
We need to prove that
To treat the case ![]() $m=0$
, we observe that
$m=0$
, we observe that ![]() $\Phi(iy) + \Phi({-}iy) = 1$
for
$\Phi(iy) + \Phi({-}iy) = 1$
for ![]() $y\in\mathbb{R}$
(see (1.6)), whence
$y\in\mathbb{R}$
(see (1.6)), whence
We proceed by induction. Observe that
 \begin{align*}& \frac {\rm d} {{\rm d} y} \left( \Phi^{m+2}(iy) + ({-}1)^{m+1} \Phi^{m+2}({-}iy) \right)\\
& \quad =(m+2) \left( \Phi^{m+1}(iy) + ({-}1)^m \Phi^{m+1}({-}iy) \right) \frac{i}{\sqrt{2\pi}} {\rm e}^{y^2/2}.\end{align*}
\begin{align*}& \frac {\rm d} {{\rm d} y} \left( \Phi^{m+2}(iy) + ({-}1)^{m+1} \Phi^{m+2}({-}iy) \right)\\
& \quad =(m+2) \left( \Phi^{m+1}(iy) + ({-}1)^m \Phi^{m+1}({-}iy) \right) \frac{i}{\sqrt{2\pi}} {\rm e}^{y^2/2}.\end{align*}
Integration by parts yields
 \begin{align*}&\lefteqn{I(m,m+1)}\\[4pt]
& \quad =-\frac{i \sqrt{2\pi}}{m+2} \int_{0}^{+\infty} y^m {\rm e}^{-(m+2) y^2/2} {\rm d} \left( \Phi^{m+2}(iy) + ({-}1)^{m+1} \Phi^{m+2}({-}iy) \right) \\[4pt]
&\quad =\frac{i \sqrt{2\pi}}{m+2} \int_{0}^{+\infty} \left( \Phi^{m+2}(iy) + ({-}1)^{m+1} \Phi^{m+2}({-}iy) \right) \left(m y^{m-1} - (m+2) y^{m+1} \right) {\rm e}^{-(m+2) y^2/2} {\rm d} y\\[4pt]
&\quad =\frac{i \sqrt{2\pi}}{m+2} \left(m I(m-1,m+2) - (m+2)I(m+1,m+2)\right).\end{align*}
\begin{align*}&\lefteqn{I(m,m+1)}\\[4pt]
& \quad =-\frac{i \sqrt{2\pi}}{m+2} \int_{0}^{+\infty} y^m {\rm e}^{-(m+2) y^2/2} {\rm d} \left( \Phi^{m+2}(iy) + ({-}1)^{m+1} \Phi^{m+2}({-}iy) \right) \\[4pt]
&\quad =\frac{i \sqrt{2\pi}}{m+2} \int_{0}^{+\infty} \left( \Phi^{m+2}(iy) + ({-}1)^{m+1} \Phi^{m+2}({-}iy) \right) \left(m y^{m-1} - (m+2) y^{m+1} \right) {\rm e}^{-(m+2) y^2/2} {\rm d} y\\[4pt]
&\quad =\frac{i \sqrt{2\pi}}{m+2} \left(m I(m-1,m+2) - (m+2)I(m+1,m+2)\right).\end{align*}
But we already know that ![]() $m I(m-1,m+2) = 0$
, whence
$m I(m-1,m+2) = 0$
, whence ![]() $I(m,m+1) = - i \sqrt{2\pi}I(m+1,m+2)$
for all
$I(m,m+1) = - i \sqrt{2\pi}I(m+1,m+2)$
for all ![]() $m\in\mathbb{N}_0$
, and the claim follows by induction.
$m\in\mathbb{N}_0$
, and the claim follows by induction.
4. Inverting the Laplace transforms
4.1. Proof of Corollary 1.1
Conditioning on the event ![]() $|X| = r$
and noting that
$|X| = r$
and noting that ![]() $|X|$
has a
$|X|$
has a ![]() $\chi$
-distribution with d degrees of freedom, we can write
$\chi$
-distribution with d degrees of freedom, we can write
 \begin{align*}\mathbb{P}[\sigma X\notin \mathop{\mathrm{Conv}}\nolimits (X_1,\ldots,X_n)]&=\int_{0}^\infty f_{n,d} (\sigma r) \frac{2^{1-(d/2)}}{\Gamma(d/2)} r^{d-1} {\rm e}^{-r^2/2} {\rm d} r\\[5pt]
&=\frac{1}{\Gamma(d/2) \sigma^d} \int_{0}^\infty f_{n,d} (\sqrt{2u}) u^{(d/2) -1} {\rm e}^{-u/\sigma^2} {\rm d} u,\end{align*}
\begin{align*}\mathbb{P}[\sigma X\notin \mathop{\mathrm{Conv}}\nolimits (X_1,\ldots,X_n)]&=\int_{0}^\infty f_{n,d} (\sigma r) \frac{2^{1-(d/2)}}{\Gamma(d/2)} r^{d-1} {\rm e}^{-r^2/2} {\rm d} r\\[5pt]
&=\frac{1}{\Gamma(d/2) \sigma^d} \int_{0}^\infty f_{n,d} (\sqrt{2u}) u^{(d/2) -1} {\rm e}^{-u/\sigma^2} {\rm d} u,\end{align*}
where we made the change of variables ![]() $\sigma r = \sqrt{2 u}$
,
$\sigma r = \sqrt{2 u}$
, ![]() ${\rm d} r = \sigma^{-1} {\rm d} u / \sqrt{2u}$
. Taking
${\rm d} r = \sigma^{-1} {\rm d} u / \sqrt{2u}$
. Taking ![]() $\lambda\coloneqq 1/\sigma^2$
and applying Theorem 1.1, we obtain
$\lambda\coloneqq 1/\sigma^2$
and applying Theorem 1.1, we obtain
which proves the theorem.
4.2. Proof of Theorem 1.2
From Corollary 1.1 and Wendel’s formula (1.11) we know that
 \begin{multline*}\int_0^{\infty} (f_{n,d}(\sqrt{2u}) - f_{n,d}(0)) u^{(d/2) - 1} {\rm e}^{-\lambda u} {\rm d} u\\=2\Gamma(d/2) \lambda^{-d/2} \left(b_{n,d-1}(1/\lambda) - \frac 1 {2^n}\binom {n}{d-1} + b_{n,d-3}(1/\lambda) - \frac 1 {2^n}\binom{n}{d-3} +\ldots\right).\end{multline*}
\begin{multline*}\int_0^{\infty} (f_{n,d}(\sqrt{2u}) - f_{n,d}(0)) u^{(d/2) - 1} {\rm e}^{-\lambda u} {\rm d} u\\=2\Gamma(d/2) \lambda^{-d/2} \left(b_{n,d-1}(1/\lambda) - \frac 1 {2^n}\binom {n}{d-1} + b_{n,d-3}(1/\lambda) - \frac 1 {2^n}\binom{n}{d-3} +\ldots\right).\end{multline*}
By the uniqueness of the Laplace transform, it suffices to show that
Recalling the formulas for ![]() $a_{n,k}(u)$
and
$a_{n,k}(u)$
and ![]() $b_{n,k}(1/\lambda)$
(see (1.10), (1.12)), we rewrite this as
$b_{n,k}(1/\lambda)$
(see (1.10), (1.12)), we rewrite this as
 \begin{multline*}\int_0^{\infty} {\rm e}^{-\lambda u} \frac 1 {\Gamma(d/2)} \left(\int_0^u {\rm e}^{-vk} F^{\prime}_{k,n-k} (v) (u-v)^{(d/2)-1} {\rm d} v\right) {\rm d} u\\= \lambda^{-d/2} \left( g_k\left({-}\frac{1}{\lambda+k}\right) g_{n-k} \left(\frac{1}{\lambda+k}\right)- \frac 1 {2^n}\right).\end{multline*}
\begin{multline*}\int_0^{\infty} {\rm e}^{-\lambda u} \frac 1 {\Gamma(d/2)} \left(\int_0^u {\rm e}^{-vk} F^{\prime}_{k,n-k} (v) (u-v)^{(d/2)-1} {\rm d} v\right) {\rm d} u\\= \lambda^{-d/2} \left( g_k\left({-}\frac{1}{\lambda+k}\right) g_{n-k} \left(\frac{1}{\lambda+k}\right)- \frac 1 {2^n}\right).\end{multline*}
The inner integral on the left-hand side is the fractional Riemann–Liouville integral of order ![]() $d/2$
of the function
$d/2$
of the function ![]() ${\rm e}^{-vk} F^{\prime}_{k,n-k} (v)$
. Recall that the fractional integral of order
${\rm e}^{-vk} F^{\prime}_{k,n-k} (v)$
. Recall that the fractional integral of order ![]() $\alpha\geq 0$
is defined by
$\alpha\geq 0$
is defined by
and its Laplace transform is just ![]() $\lambda^{-\alpha}$
times the Laplace transform of f:
$\lambda^{-\alpha}$
times the Laplace transform of f:
Using this property, we deduce that it is sufficient to prove that
Writing ![]() $\mu\coloneqq \lambda + k$
, we rewrite this as
$\mu\coloneqq \lambda + k$
, we rewrite this as
Observe that ![]() $\lim_{u\downarrow 0}F_{k,n-k}(u) = 2^{-n}$
. This follows from (1.13) by observing that
$\lim_{u\downarrow 0}F_{k,n-k}(u) = 2^{-n}$
. This follows from (1.13) by observing that
and using dominated convergence. Using partial integration, we can write the above as
Recall from (1.13) that ![]() $F_{k,n-k}(u) = \int_{0}^{u} h_{n-k}^{(1)} (w) h_k^{(2)} (u-w) {\rm d} w$
, where
$F_{k,n-k}(u) = \int_{0}^{u} h_{n-k}^{(1)} (w) h_k^{(2)} (u-w) {\rm d} w$
, where
Let us compute the Laplace transforms of ![]() $h_{n-k}^{(1)}$
and
$h_{n-k}^{(1)}$
and ![]() $h_{k}^{(2)}$
:
$h_{k}^{(2)}$
:
 \begin{align*}\int_0^{\infty} {\rm e}^{-\mu w} h_{n-k}^{(1)}(w) {\rm d} w&=\int_0^{\infty} {\rm e}^{-\mu w} \left(\Phi^{n-k}(\sqrt{2 w}) + \Phi^{n-k}({-}\sqrt{2 w})\right) \frac{{\rm d} w}{2\sqrt {\pi w}}\\[4pt]
&=\frac 1 {\sqrt{2\pi \mu}} \int_0^{\infty} {\rm e}^{-y^2/2} \left(\Phi^{n-k}\left(\frac{y}{\sqrt \mu}\right) + \Phi^{n-k}\left({-}\frac{y}{\sqrt \mu}\right)\right) {\rm d} y\\[4pt]
&=\mu^{-1/2} g_{n-k}(1/\mu),\end{align*}
\begin{align*}\int_0^{\infty} {\rm e}^{-\mu w} h_{n-k}^{(1)}(w) {\rm d} w&=\int_0^{\infty} {\rm e}^{-\mu w} \left(\Phi^{n-k}(\sqrt{2 w}) + \Phi^{n-k}({-}\sqrt{2 w})\right) \frac{{\rm d} w}{2\sqrt {\pi w}}\\[4pt]
&=\frac 1 {\sqrt{2\pi \mu}} \int_0^{\infty} {\rm e}^{-y^2/2} \left(\Phi^{n-k}\left(\frac{y}{\sqrt \mu}\right) + \Phi^{n-k}\left({-}\frac{y}{\sqrt \mu}\right)\right) {\rm d} y\\[4pt]
&=\mu^{-1/2} g_{n-k}(1/\mu),\end{align*}
where we made the change of variables ![]() $w = y^2/(2\mu)$
in the second step and recalled (1.19) in the last step. Arguing in an analogous way, we obtain
$w = y^2/(2\mu)$
in the second step and recalled (1.19) in the last step. Arguing in an analogous way, we obtain
 \begin{align*}\int_0^{\infty} {\rm e}^{-\mu w} h_{k}^{(2)}(w) {\rm d} w&=\int_0^{\infty} {\rm e}^{-\mu w} \left(\Phi^{k}(i\sqrt{2 w}) + \Phi^{k}({-}i\sqrt{2 w})\right) \frac{{\rm d} w}{2\sqrt {\pi w}}\\[4pt]
&=\frac 1 {\sqrt{2\pi \mu}} \int_0^{\infty} {\rm e}^{-y^2/2} \left(\Phi^{k}\left(i\frac{y}{\sqrt \mu}\right) + \Phi^{k}\left({-}i\frac{y}{\sqrt \mu}\right)\right) {\rm d} y\\[4pt]
&=\mu^{-1/2} g_{k}({-}1/\mu).\end{align*}
\begin{align*}\int_0^{\infty} {\rm e}^{-\mu w} h_{k}^{(2)}(w) {\rm d} w&=\int_0^{\infty} {\rm e}^{-\mu w} \left(\Phi^{k}(i\sqrt{2 w}) + \Phi^{k}({-}i\sqrt{2 w})\right) \frac{{\rm d} w}{2\sqrt {\pi w}}\\[4pt]
&=\frac 1 {\sqrt{2\pi \mu}} \int_0^{\infty} {\rm e}^{-y^2/2} \left(\Phi^{k}\left(i\frac{y}{\sqrt \mu}\right) + \Phi^{k}\left({-}i\frac{y}{\sqrt \mu}\right)\right) {\rm d} y\\[4pt]
&=\mu^{-1/2} g_{k}({-}1/\mu).\end{align*}
Since the Laplace transform of the convolution is the product of the Laplace transforms, we arrive at (4.1), which completes the proof.
4.3. Proof of Theorem 1.5
Corollary 1.1 with ![]() $d=2$
states that for all
$d=2$
states that for all ![]() $\lambda>0$
,
$\lambda>0$
,
where we used (1.10) and the fact that ![]() $g_1(r) = 1/2$
. Recalling the formula for
$g_1(r) = 1/2$
. Recalling the formula for ![]() $g_{n-1}$
(see (1.19)), we arrive at
$g_{n-1}$
(see (1.19)), we arrive at
 \begin{align*}\int_0^{\infty} f_{n,2}(\sqrt{2u}) {\rm e}^{-\lambda u} {\rm d} u&=\frac {n}{\lambda\sqrt{2\pi}} \int_0^{\infty} \left(\Phi^{n-1}\left(\frac {x}{\sqrt{1+\lambda}}\right) + \Phi^{n-1}\left({-}\frac {x}{\sqrt{1+\lambda}}\right)\right) {\rm e}^{-x^2/2}{\rm d} x\\[9pt]
&=\frac{\sqrt{1+\lambda}}{\lambda} \cdot \frac {n}{\sqrt{2\pi}} \int_0^{\infty} \frac{\Phi^{n-1}(\sqrt{2z}) + \Phi^{n-1}({-}\sqrt{2z})}{\sqrt{2z}} {\rm e}^{-z} {\rm e}^{-z\lambda}{\rm d} z\\[4pt]
&=\frac{\sqrt{1+\lambda}}{\lambda} \cdot \int_0^{\infty} f_{M_n^2/2}(z) {\rm e}^{-z\lambda} {\rm d} z,\end{align*}
\begin{align*}\int_0^{\infty} f_{n,2}(\sqrt{2u}) {\rm e}^{-\lambda u} {\rm d} u&=\frac {n}{\lambda\sqrt{2\pi}} \int_0^{\infty} \left(\Phi^{n-1}\left(\frac {x}{\sqrt{1+\lambda}}\right) + \Phi^{n-1}\left({-}\frac {x}{\sqrt{1+\lambda}}\right)\right) {\rm e}^{-x^2/2}{\rm d} x\\[9pt]
&=\frac{\sqrt{1+\lambda}}{\lambda} \cdot \frac {n}{\sqrt{2\pi}} \int_0^{\infty} \frac{\Phi^{n-1}(\sqrt{2z}) + \Phi^{n-1}({-}\sqrt{2z})}{\sqrt{2z}} {\rm e}^{-z} {\rm e}^{-z\lambda}{\rm d} z\\[4pt]
&=\frac{\sqrt{1+\lambda}}{\lambda} \cdot \int_0^{\infty} f_{M_n^2/2}(z) {\rm e}^{-z\lambda} {\rm d} z,\end{align*}
where we used the change of variables ![]() $x/\sqrt {1+\lambda} = \sqrt{2z}$
, and
$x/\sqrt {1+\lambda} = \sqrt{2z}$
, and ![]() $f_{M_n^2/2}$
denotes the density of the random variable
$f_{M_n^2/2}$
denotes the density of the random variable ![]() $\frac 12 M_n^2$
, namely
$\frac 12 M_n^2$
, namely
where ![]() $z>0$
. The inverse Laplace transform of
$z>0$
. The inverse Laplace transform of ![]() $\sqrt{1+\lambda} /\lambda$
is given by
$\sqrt{1+\lambda} /\lambda$
is given by ![]() $(2\Phi(\sqrt{2z}) - 1) + {\rm e}^{-z}/\sqrt{\pi z}$
. Observe that the first summand is just the distribution function
$(2\Phi(\sqrt{2z}) - 1) + {\rm e}^{-z}/\sqrt{\pi z}$
. Observe that the first summand is just the distribution function ![]() $F_{\xi^2/2}$
of
$F_{\xi^2/2}$
of ![]() $\frac 12 \xi^2$
(with
$\frac 12 \xi^2$
(with ![]() $\xi$
standard normal), whereas the second summand is the density
$\xi$
standard normal), whereas the second summand is the density ![]() $f_{\xi^2/2} = F^{\prime}_{\xi^2/2}$
of the same random variable. Since the inverse Laplace transform of a product is a convolution of the inverse Laplace transforms, we arrive at
$f_{\xi^2/2} = F^{\prime}_{\xi^2/2}$
of the same random variable. Since the inverse Laplace transform of a product is a convolution of the inverse Laplace transforms, we arrive at
 \begin{align*}f_{n,2}(\sqrt{2u})&= \int_{0}^{u} f_{M_n^2/2} (z) F_{\xi^2/2}(u-z) {\rm d} z + \int_{0}^{u} f_{M_n^2/2} (z) f_{\xi^2/2}(u-z) {\rm d} z\\[4pt]
&=\mathbb{P}[ M_{n}^2 + \xi^2 \leq 2u] + \frac {{\rm d}}{{\rm d} u}\mathbb{P}[ M_{n}^2 + \xi^2 \leq 2u],\end{align*}
\begin{align*}f_{n,2}(\sqrt{2u})&= \int_{0}^{u} f_{M_n^2/2} (z) F_{\xi^2/2}(u-z) {\rm d} z + \int_{0}^{u} f_{M_n^2/2} (z) f_{\xi^2/2}(u-z) {\rm d} z\\[4pt]
&=\mathbb{P}[ M_{n}^2 + \xi^2 \leq 2u] + \frac {{\rm d}}{{\rm d} u}\mathbb{P}[ M_{n}^2 + \xi^2 \leq 2u],\end{align*}
which proves the first formula in Theorem 1.5. To verify the second formula, observe that by the change of variables ![]() $x\coloneqq \sqrt {2z}$
and then
$x\coloneqq \sqrt {2z}$
and then ![]() $y: = x/\sqrt {2u}$
,
$y: = x/\sqrt {2u}$
,
 \begin{align*}\int_{0}^{u} f_{M_n^2/2} (z) f_{\xi^2/2}(u-z) {\rm d} z&=\frac {n}{\sqrt{2\pi}} \int_0^u \frac{\Phi^{n-1}(\sqrt{2z}) + \Phi^{n-1}({-}\sqrt{2z})}{\sqrt{2z}} {\rm e}^{-z} \frac{{\rm e}^{-(u-z)}}{\sqrt \pi \sqrt{u-z}} {\rm d} z\\[4pt]
&=n{\rm e}^{-u} \int_{0}^{\sqrt{2u}} \frac{\Phi^{n-1}(x) + \Phi^{n-1}({-}x)}{\pi \sqrt{2u-x^2}} {\rm d} x\\[4pt]
&=n{\rm e}^{-u} \int_{-\sqrt{2u}}^{\sqrt{2u}} \frac{\Phi^{n-1}(x) }{\pi \sqrt{2u-x^2}} {\rm d} x\\[4pt]
&=n{\rm e}^{-u} \int_{-1}^{1} \frac{\Phi^{n-1}(\sqrt {2u} y) }{\pi \sqrt{1-y^2}} {\rm d} y.\end{align*}
\begin{align*}\int_{0}^{u} f_{M_n^2/2} (z) f_{\xi^2/2}(u-z) {\rm d} z&=\frac {n}{\sqrt{2\pi}} \int_0^u \frac{\Phi^{n-1}(\sqrt{2z}) + \Phi^{n-1}({-}\sqrt{2z})}{\sqrt{2z}} {\rm e}^{-z} \frac{{\rm e}^{-(u-z)}}{\sqrt \pi \sqrt{u-z}} {\rm d} z\\[4pt]
&=n{\rm e}^{-u} \int_{0}^{\sqrt{2u}} \frac{\Phi^{n-1}(x) + \Phi^{n-1}({-}x)}{\pi \sqrt{2u-x^2}} {\rm d} x\\[4pt]
&=n{\rm e}^{-u} \int_{-\sqrt{2u}}^{\sqrt{2u}} \frac{\Phi^{n-1}(x) }{\pi \sqrt{2u-x^2}} {\rm d} x\\[4pt]
&=n{\rm e}^{-u} \int_{-1}^{1} \frac{\Phi^{n-1}(\sqrt {2u} y) }{\pi \sqrt{1-y^2}} {\rm d} y.\end{align*}
The integral equals ![]() $\mathbb{P}[M_{n-1}\leq \sqrt{2u} W]$
since
$\mathbb{P}[M_{n-1}\leq \sqrt{2u} W]$
since ![]() $\Phi^{n-1}$
is the distribution function of
$\Phi^{n-1}$
is the distribution function of ![]() $M_{n-1}$
.
$M_{n-1}$
.
5. Proof of Theorem 1.6
The proof relies strongly on the ideas of Baryshnikov and Vitale [Reference Baryshnikov and Vitale5] combined with the Bartlett decomposition of the Gaussian matrix and Theorem 1.1.
Step 1: Bartlett decomposition of a Gaussian matrix. Let O be a random orthogonal matrix distributed according to the Haar probability measure on the group O(n). Independently of O, let L be a random lower-triangular ![]() $n\times n$
matrix with a.s. positive entries on the diagonal and the following distribution. The entries of L are independent; the squared diagonal entries have
$n\times n$
matrix with a.s. positive entries on the diagonal and the following distribution. The entries of L are independent; the squared diagonal entries have ![]() $\chi^2$
-distributions with
$\chi^2$
-distributions with ![]() $n,n-1,\ldots,1$
degrees of freedom, whereas the entries below the diagonal are standard normal. Define an
$n,n-1,\ldots,1$
degrees of freedom, whereas the entries below the diagonal are standard normal. Define an ![]() $n\times n$
matrix G by
$n\times n$
matrix G by
It is known (Bartlett decomposition) that the entries of G are independent standard Gaussian random variables.
Step 2: Relating the Goodman–Pollack model to the Gaussian polytope. Consider an ![]() $n\times (n+1)$
matrix S whose columns are the vectors
$n\times (n+1)$
matrix S whose columns are the vectors ![]() $v_1,\ldots,v_{n+1}$
. Recall also that
$v_1,\ldots,v_{n+1}$
. Recall also that ![]() $\Pi$
is the
$\Pi$
is the ![]() $d\times n$
matrix of the projection from
$d\times n$
matrix of the projection from ![]() $\mathbb{R}^n$
onto the linear subspace
$\mathbb{R}^n$
onto the linear subspace ![]() $\mathbb{R}^d$
spanned by
$\mathbb{R}^d$
spanned by ![]() $e_1,\ldots,e_d$
. Note that
$e_1,\ldots,e_d$
. Note that ![]() $\Pi$
consists of an identity matrix
$\Pi$
consists of an identity matrix ![]() $I_d$
extended by a
$I_d$
extended by a ![]() $d\times (n-d)$
zero matrix. Following Baryshnikov and Vitale [Reference Baryshnikov and Vitale5], consider the
$d\times (n-d)$
zero matrix. Following Baryshnikov and Vitale [Reference Baryshnikov and Vitale5], consider the ![]() $d\times (n+1)$
matrix
$d\times (n+1)$
matrix
where ![]() $\tilde L$
is a lower-triangular
$\tilde L$
is a lower-triangular ![]() $d\times d$
matrix obtained from L by removing all rows and columns except the first d ones. The last equality follows from the simple identity
$d\times d$
matrix obtained from L by removing all rows and columns except the first d ones. The last equality follows from the simple identity ![]() $\Pi L = \tilde L \Pi$
. It follows from the corresponding properties of L that the matrix
$\Pi L = \tilde L \Pi$
. It follows from the corresponding properties of L that the matrix ![]() $\tilde L$
is lower-triangular, its entries are independent, the squared diagonal entries have
$\tilde L$
is lower-triangular, its entries are independent, the squared diagonal entries have ![]() $\chi^2$
-distributions with
$\chi^2$
-distributions with ![]() $n,n-1,\ldots, n-d$
degrees of freedom, and the entries below the diagonal are standard Gaussian.
$n,n-1,\ldots, n-d$
degrees of freedom, and the entries below the diagonal are standard Gaussian.
Observe that the matrices ![]() $\tilde L$
and
$\tilde L$
and ![]() $\Pi O S$
are stochastically independent, and the columns of the latter matrix are the vectors
$\Pi O S$
are stochastically independent, and the columns of the latter matrix are the vectors ![]() $\Pi O v_1, \ldots, \Pi O v_{n+1}$
, whose convex hull is the Goodman–Pollack polytope
$\Pi O v_1, \ldots, \Pi O v_{n+1}$
, whose convex hull is the Goodman–Pollack polytope ![]() $\mathcal{Q}_{n+1,d}$
.
$\mathcal{Q}_{n+1,d}$
.
Denote the columns of the matrix ![]() $\tilde S$
by
$\tilde S$
by ![]() $Y_{\bullet, 1},\ldots, Y_{\bullet, (n+1)}$
. Let us write
$Y_{\bullet, 1},\ldots, Y_{\bullet, (n+1)}$
. Let us write ![]() $Y_{\bullet, j} = (Y_{1,j}, \ldots, Y_{d,j})^\top$
,
$Y_{\bullet, j} = (Y_{1,j}, \ldots, Y_{d,j})^\top$
, ![]() $1\leq j\leq n+1$
. It follows from the formula
$1\leq j\leq n+1$
. It follows from the formula ![]() $\tilde S = \Pi G S$
that the random variables
$\tilde S = \Pi G S$
that the random variables ![]() $Y_{i,j}$
,
$Y_{i,j}$
, ![]() $1\leq i\leq d$
,
$1\leq i\leq d$
, ![]() $1\leq j\leq n+1$
, are jointly Gaussian with mean zero. Let us compute their covariances. Writing
$1\leq j\leq n+1$
, are jointly Gaussian with mean zero. Let us compute their covariances. Writing ![]() $G = (g_{i,j})_{1\leq i \leq n, 1\leq j\leq n}$
with independent standard Gaussian entries
$G = (g_{i,j})_{1\leq i \leq n, 1\leq j\leq n}$
with independent standard Gaussian entries ![]() $g_{i,j}$
, we observe that
$g_{i,j}$
, we observe that ![]() $\Pi G = (g_{i,j})_{1\leq i \leq d, 1\leq j \leq n}$
, and hence
$\Pi G = (g_{i,j})_{1\leq i \leq d, 1\leq j \leq n}$
, and hence
 \begin{align*}\mathbb E [Y_{i_1, j_1} Y_{i_2, j_2}]&=\mathbb E \left[\langle (g_{i_1, 1}, \ldots, g_{i_1, n})^\top, v_{j_1} \rangle \langle (g_{i_2, 1}, \ldots, g_{i_2, n})^\top, v_{j_2} \rangle \right]\\[4pt]
&=\begin{cases}0 &\text{ if } i_1\neq i_2,\\[4pt]
\langle v_{j_1}, v_{j_2} \rangle &\text{ if } i_1 = i_2.\end{cases}\end{align*}
\begin{align*}\mathbb E [Y_{i_1, j_1} Y_{i_2, j_2}]&=\mathbb E \left[\langle (g_{i_1, 1}, \ldots, g_{i_1, n})^\top, v_{j_1} \rangle \langle (g_{i_2, 1}, \ldots, g_{i_2, n})^\top, v_{j_2} \rangle \right]\\[4pt]
&=\begin{cases}0 &\text{ if } i_1\neq i_2,\\[4pt]
\langle v_{j_1}, v_{j_2} \rangle &\text{ if } i_1 = i_2.\end{cases}\end{align*}
By the properties of the regular simplex we have ![]() $\langle v_{j_1}, v_{j_2}\rangle = -1/n <0$
provided that
$\langle v_{j_1}, v_{j_2}\rangle = -1/n <0$
provided that ![]() $j_1\neq j_2$
. Let W be a standard Gaussian random vector on
$j_1\neq j_2$
. Let W be a standard Gaussian random vector on ![]() $\mathbb{R}^d$
independent of L and O (and hence of G and
$\mathbb{R}^d$
independent of L and O (and hence of G and ![]() $\tilde S$
). It follows that
$\tilde S$
). It follows that
are mutually independent standard Gaussian random vectors on ![]() $\mathbb{R}^d$
. Their convex hull has the same distribution as the Gaussian polytope and will be denoted by
$\mathbb{R}^d$
. Their convex hull has the same distribution as the Gaussian polytope and will be denoted by ![]() $\mathcal{P}_{n+1,d}$
for this reason. Summarizing everything, we obtain the identity
$\mathcal{P}_{n+1,d}$
for this reason. Summarizing everything, we obtain the identity
 \begin{align} \tilde L \mathcal{Q}_{n+1,d} & = \mathop{\mathrm{Conv}}\nolimits(\tilde L \Pi O v_1,\ldots, \tilde L \Pi O v_{n+1})\nonumber\\[5pt]
& = \mathop{\mathrm{Conv}}\nolimits(Y_{\bullet, 1},\ldots, Y_{\bullet, (n+1)}) = \sqrt{\frac{n+1}{n}} \mathcal{P}_{n+1,d} - \frac W{ \sqrt{n}},\end{align}
\begin{align} \tilde L \mathcal{Q}_{n+1,d} & = \mathop{\mathrm{Conv}}\nolimits(\tilde L \Pi O v_1,\ldots, \tilde L \Pi O v_{n+1})\nonumber\\[5pt]
& = \mathop{\mathrm{Conv}}\nolimits(Y_{\bullet, 1},\ldots, Y_{\bullet, (n+1)}) = \sqrt{\frac{n+1}{n}} \mathcal{P}_{n+1,d} - \frac W{ \sqrt{n}},\end{align}
where ![]() $\tilde L$
, W,
$\tilde L$
, W, ![]() $\mathcal{Q}_{n+1,d}$
are independent. The fact that
$\mathcal{Q}_{n+1,d}$
are independent. The fact that ![]() $\mathcal{P}_{n+1,d}$
can be obtained from
$\mathcal{P}_{n+1,d}$
can be obtained from ![]() $\mathcal{Q}_{n+1,d}$
by a random affine transformation stochastically independent from
$\mathcal{Q}_{n+1,d}$
by a random affine transformation stochastically independent from ![]() $\mathcal{Q}_{n+1,d}$
was proved by Baryshnikov and Vitale [Reference Baryshnikov and Vitale5]. We rederived it because we shall need the explicit form of the affine transformation in what follows.
$\mathcal{Q}_{n+1,d}$
was proved by Baryshnikov and Vitale [Reference Baryshnikov and Vitale5]. We rederived it because we shall need the explicit form of the affine transformation in what follows.
Step 3: Relating the non-absorption probabilities for ![]() $\mathcal{P}_{n+1,d}$
and
$\mathcal{P}_{n+1,d}$
and ![]() $\mathcal{Q}_{n+1,d}$
. Let now X be a standard Gaussian vector on
$\mathcal{Q}_{n+1,d}$
. Let now X be a standard Gaussian vector on ![]() $\mathbb{R}^d$
which is independent of everything else. We know from Theorem 1.1 that for every
$\mathbb{R}^d$
which is independent of everything else. We know from Theorem 1.1 that for every ![]() $\sigma^2\geq 0$
,
$\sigma^2\geq 0$
,
It follows from (5.2) that
 \begin{equation*}\mathbb{P}\left[ \sqrt{\frac{n+1}{n}} \sigma X - \frac W{ \sqrt{n}} \notin \tilde L \mathcal{Q}_{n+1,d}\right] = 2(b_{n+1,d-1}(\sigma^2) + b_{n+1,d-3}(\sigma^2) +\ldots).\end{equation*}
\begin{equation*}\mathbb{P}\left[ \sqrt{\frac{n+1}{n}} \sigma X - \frac W{ \sqrt{n}} \notin \tilde L \mathcal{Q}_{n+1,d}\right] = 2(b_{n+1,d-1}(\sigma^2) + b_{n+1,d-3}(\sigma^2) +\ldots).\end{equation*}
Introducing the standard normal d-dimensional vector
 \begin{equation*}\xi \coloneqq \left(\frac{n+1}{n}\sigma^2 + \frac 1n\right)^{-1/2} \left(\sqrt{\frac{n+1}{n}} \sigma X - \frac W{ \sqrt{n}}\right)\end{equation*}
\begin{equation*}\xi \coloneqq \left(\frac{n+1}{n}\sigma^2 + \frac 1n\right)^{-1/2} \left(\sqrt{\frac{n+1}{n}} \sigma X - \frac W{ \sqrt{n}}\right)\end{equation*}
(which is independent of ![]() $\tilde L$
and
$\tilde L$
and ![]() $\mathcal{Q}_{n+1,d}$
), we can rewrite the above as
$\mathcal{Q}_{n+1,d}$
), we can rewrite the above as
 \begin{equation*}\mathbb{P}\left[ \sqrt{\frac{n+1}{n}\sigma^2 + \frac 1n} \cdot \xi \notin \tilde L \mathcal{Q}_{n+1,d}\right] = 2(b_{n+1,d-1}(\sigma^2) + b_{n+1,d-3}(\sigma^2) +\ldots).\end{equation*}
\begin{equation*}\mathbb{P}\left[ \sqrt{\frac{n+1}{n}\sigma^2 + \frac 1n} \cdot \xi \notin \tilde L \mathcal{Q}_{n+1,d}\right] = 2(b_{n+1,d-1}(\sigma^2) + b_{n+1,d-3}(\sigma^2) +\ldots).\end{equation*}
Let ![]() $Q\in O(d)$
be a deterministic orthogonal matrix. We claim that the random set
$Q\in O(d)$
be a deterministic orthogonal matrix. We claim that the random set ![]() $\tilde L \mathcal{Q}_{n+1,d}$
is invariant with respect to orthogonal transformations; that is,
$\tilde L \mathcal{Q}_{n+1,d}$
is invariant with respect to orthogonal transformations; that is,
Since ![]() $\mathcal{Q}_{n+1,d}$
is defined as the convex hull of the columns of the matrix
$\mathcal{Q}_{n+1,d}$
is defined as the convex hull of the columns of the matrix ![]() $\Pi O S$
, it suffices to show that
$\Pi O S$
, it suffices to show that ![]() $Q \tilde L \Pi O S \stackrel{d}{=} \tilde L \Pi O S$
, or, equivalently,
$Q \tilde L \Pi O S \stackrel{d}{=} \tilde L \Pi O S$
, or, equivalently, ![]() $Q \Pi G S \stackrel{d}{=} \Pi G S$
; see (5.1). Let
$Q \Pi G S \stackrel{d}{=} \Pi G S$
; see (5.1). Let ![]() $Q'\in O(n)$
be a natural extension of Q from
$Q'\in O(n)$
be a natural extension of Q from ![]() $\mathbb{R}^d$
to
$\mathbb{R}^d$
to ![]() $\mathbb{R}^n$
defined by
$\mathbb{R}^n$
defined by
Then ![]() $Q \Pi = \Pi Q'$
, and hence it suffices to show that
$Q \Pi = \Pi Q'$
, and hence it suffices to show that ![]() $\Pi Q' G S \stackrel{d}{=} \Pi G S$
. However, since the entries of G are independent standard Gaussian and the matrix Q’ is orthogonal, it is easy to check that
$\Pi Q' G S \stackrel{d}{=} \Pi G S$
. However, since the entries of G are independent standard Gaussian and the matrix Q’ is orthogonal, it is easy to check that ![]() $Q' G \stackrel{d}{=} G$
, thus proving (5.3).
$Q' G \stackrel{d}{=} G$
, thus proving (5.3).
Let ![]() $R_1 \coloneqq |\xi|$
, so that
$R_1 \coloneqq |\xi|$
, so that ![]() $R^2_1$
has
$R^2_1$
has ![]() $\chi^2$
distribution with d degrees of freedom. By the orthogonal invariance of the random set
$\chi^2$
distribution with d degrees of freedom. By the orthogonal invariance of the random set ![]() $\tilde L \mathcal{Q}_{n+1,d}$
, we can replace
$\tilde L \mathcal{Q}_{n+1,d}$
, we can replace ![]() $\xi$
by, say,
$\xi$
by, say, ![]() $R_1 e_{n-d}$
, thus obtaining
$R_1 e_{n-d}$
, thus obtaining
 \begin{equation*}\mathbb{P}\left[ \sqrt{\frac{n+1}{n}\sigma^2 + \frac 1n} \cdot R_1 e_{n-d} \notin \tilde L \mathcal{Q}_{n+1,d}\right] = 2(b_{n+1,d-1}(\sigma^2) + b_{n+1,d-3}(\sigma^2) +\ldots).\end{equation*}
\begin{equation*}\mathbb{P}\left[ \sqrt{\frac{n+1}{n}\sigma^2 + \frac 1n} \cdot R_1 e_{n-d} \notin \tilde L \mathcal{Q}_{n+1,d}\right] = 2(b_{n+1,d-1}(\sigma^2) + b_{n+1,d-3}(\sigma^2) +\ldots).\end{equation*}
Observe that ![]() $R_2 \coloneqq |\tilde L^{-1} e_{n-d}|^{-1}$
satisfies
$R_2 \coloneqq |\tilde L^{-1} e_{n-d}|^{-1}$
satisfies ![]() $R_2^2 \sim \chi_{n-d+1}^2$
because of the structure of the lower-triangular matrix
$R_2^2 \sim \chi_{n-d+1}^2$
because of the structure of the lower-triangular matrix ![]() $\tilde L$
. The random set
$\tilde L$
. The random set ![]() $\mathcal{Q}_{n+1,d}$
is also orthogonally invariant (which follows from its definition); hence
$\mathcal{Q}_{n+1,d}$
is also orthogonally invariant (which follows from its definition); hence
 \begin{equation*}\mathbb{P}\left[\sqrt{\frac{n+1}{n}\sigma^2 + \frac 1n} \cdot \frac{R_1}{R_2} e_1 \notin \mathcal{Q}_{n+1,d}\right] = 2(b_{n+1,d-1}(\sigma^2) + b_{n+1,d-3}(\sigma^2) +\ldots).\end{equation*}
\begin{equation*}\mathbb{P}\left[\sqrt{\frac{n+1}{n}\sigma^2 + \frac 1n} \cdot \frac{R_1}{R_2} e_1 \notin \mathcal{Q}_{n+1,d}\right] = 2(b_{n+1,d-1}(\sigma^2) + b_{n+1,d-3}(\sigma^2) +\ldots).\end{equation*}
The random variables ![]() $R_1\sim \chi_d$
and
$R_1\sim \chi_d$
and ![]() $R_2\sim \chi_{n-d+1}$
are independent (because
$R_2\sim \chi_{n-d+1}$
are independent (because ![]() $\xi$
and
$\xi$
and ![]() $\tilde L$
are independent); hence the density of
$\tilde L$
are independent); hence the density of ![]() $R_1/R_2$
is given by
$R_1/R_2$
is given by
 \begin{equation*}h(u) = \frac{2 u^{d-1} (1+u^2)^{-(n+1)/2}}{B\left(\frac d2, \frac{n-d+1}{2}\right)}, \quad u\geq 0.\end{equation*}
\begin{equation*}h(u) = \frac{2 u^{d-1} (1+u^2)^{-(n+1)/2}}{B\left(\frac d2, \frac{n-d+1}{2}\right)}, \quad u\geq 0.\end{equation*}
We can finally rewrite the above as
 \begin{equation*}\int_{0}^{\infty} h(u) f_{n+1,d}^* \left(\sqrt{\frac{n+1}{n}\sigma^2 + \frac 1n} \cdot u\right) {\rm d} u = 2(b_{n+1,d-1}(\sigma^2) + b_{n+1,d-3}(\sigma^2) +\ldots),\end{equation*}
\begin{equation*}\int_{0}^{\infty} h(u) f_{n+1,d}^* \left(\sqrt{\frac{n+1}{n}\sigma^2 + \frac 1n} \cdot u\right) {\rm d} u = 2(b_{n+1,d-1}(\sigma^2) + b_{n+1,d-3}(\sigma^2) +\ldots),\end{equation*}
and Theorem 1.6 follows after replacing ![]() $n+1$
by n.
$n+1$
by n.
Remark 5.1. If instead of the regular simplex with ![]() $n+1$
vertices inscribed into
$n+1$
vertices inscribed into ![]() $\mathbb S^{n-1}$
we rotate and project the regular simplex
$\mathbb S^{n-1}$
we rotate and project the regular simplex ![]() $\mathop{\mathrm{Conv}}\nolimits (e_1,\ldots,e_n)$
, the proof simplifies. The random vectors
$\mathop{\mathrm{Conv}}\nolimits (e_1,\ldots,e_n)$
, the proof simplifies. The random vectors ![]() $Y_{\bullet, 1}, \ldots, Y_{\bullet, n}$
(their number is n rather than
$Y_{\bullet, 1}, \ldots, Y_{\bullet, n}$
(their number is n rather than ![]() $n+1$
) are independent standard Gaussian and there is no need of introducing W.
$n+1$
) are independent standard Gaussian and there is no need of introducing W.
Acknowledgement
Z. K. is grateful to Alexander Marynych for suggesting the use of partial integration in the proof of Proposition 1.5.