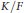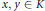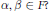Refine search
Actions for selected content:
2 results
On the Theorem of the Primitive Element with Applications to the Representation Theory of Associative and Lie Algebras
-
- Journal:
- Canadian Mathematical Bulletin / Volume 57 / Issue 4 / 01 December 2014
- Published online by Cambridge University Press:
- 20 November 2018, pp. 735-748
- Print publication:
- 01 December 2014
-
- Article
-
- You have access
- Export citation
On the Decomposition of Nonsingular CS-Modules
-
- Journal:
- Canadian Mathematical Bulletin / Volume 39 / Issue 3 / 01 September 1996
- Published online by Cambridge University Press:
- 20 November 2018, pp. 257-265
- Print publication:
- 01 September 1996
-
- Article
-
- You have access
- Export citation