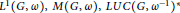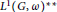Skip to main content Accessibility help
×
  1. Home
  2. Search

Refine search

Refine search

Access:
Content type:
Publication date:
Apply   From and To filters
Subject: Show more
Journals Show more
Publishers: Show more
Societies Show more
Series: Show more
Collections: Show more

Actions for selected content:

Select all | Deselect all
  • View selected items
  • Export citations
  • Download PDF (zip)
  • Save to Kindle
  • Save to Dropbox
  • Save to Google Drive

Save Search

You can save your searches here and later view and run them again in "My saved searches".

Please provide a title, maximum of 40 characters.
Cancel
×

2 results

  • THE COMPLEXITY OF TOPOLOGICAL GROUP ISOMORPHISM

  • ALEXANDER S. KECHRIS, ANDRÉ NIES, KATRIN TENT
  • Journal:
    The Journal of Symbolic Logic / Volume 83 / Issue 3 / September 2018
    Published online by Cambridge University Press:
    23 October 2018, pp. 1190-1203
    Print publication:
    September 2018

  • We study the complexity of the topological isomorphism relation for various classes of closed subgroups of the group of permutations of the natural numbers. We use the setting of Borel reducibility between equivalence relations on Borel spaces. For profinite, locally compact, and Roelcke precompact groups, we show that the complexity is the same as the one of countable graph isomorphism. For oligomorphic groups, we merely establish this as an upper bound.

  • Bipositive Isomorphisms Between Beurling Algebras and Between their Second Dual Algebras

  • F. Ghahramani, S. Zadeh
  • Journal:
    Canadian Journal of Mathematics / Volume 69 / Issue 1 / 01 February 2017
    Published online by Cambridge University Press:
    20 November 2018, pp. 3-20
    Print publication:
    01 February 2017
    • Article
      • You have access
    • PDF
    • Export citation

  • Let $G$ be a locally compact group and let $\omega$ be a continuous weight on $G$ . We show that for each of the Banach algebras ${{L}^{1}}\left( G,\,\omega\right),\,M\left( G,\,\omega\right),\,LUC{{\left( G,\,{{\omega }^{-1}} \right)}^{*}}$ , and ${{L}^{1}}{{\left( G,\,\omega\right)}^{**}}$ , the order structure combined with the algebra structure determines the weighted group.