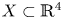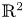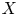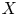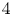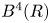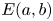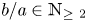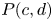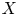The Hamiltonian shape invariant of a domain 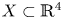$X \subset \mathbb {R}^4$, as a subset of 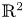$\mathbb {R}^2$, describes the product Lagrangian tori which may be embedded in 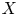$X$. We provide necessary and sufficient conditions to determine whether or not a path in the shape invariant can lift, that is, be realized as a smooth family of embedded Lagrangian tori, when 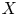$X$ is a basic 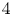$4$-dimensional toric domain such as a ball 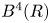$B^4(R)$, an ellipsoid 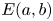$E(a,b)$ with 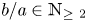${b}/{a} \in \mathbb {N}_{\geq ~2}$, or a polydisk 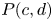$P(c,d)$. As applications, via the path lifting, we can detect knotted embeddings of product Lagrangian tori in many toric 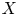$X$. We also obtain novel obstructions to symplectic embeddings between domains that are more general than toric concave or toric convex.

We prove packing stability for rational symplectic manifolds. This will rely on a general symplectic embedding result for ellipsoids which assumes only that there is no volume obstruction and that the domain is sufficiently thin relative to the target. We also obtain easily computable bounds for the Embedded Contact Homology capacities which are sufficient to imply the existence of some symplectic volume filling embeddings in dimension 4.