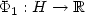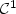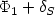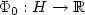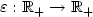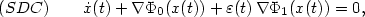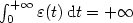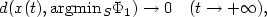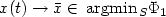Let H be a real Hilbert space, $\Phi_1: H\to \xR$ 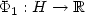 a convex function of class ${\mathcal C}^1$
a convex function of class ${\mathcal C}^1$ 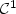 that we wish to minimize under the convexconstraint S.A classical approach consists in following the trajectories of the generalizedsteepest descent system (cf. Brézis [CITE]) appliedto the non-smooth function $\Phi_1+\delta_S$
that we wish to minimize under the convexconstraint S.A classical approach consists in following the trajectories of the generalizedsteepest descent system (cf. Brézis [CITE]) appliedto the non-smooth function $\Phi_1+\delta_S$ 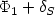 . Following Antipin [1], it is also possible to use a continuous gradient-projection system.We propose here an alternative method as follows:given a smooth convex function $\Phi_0: H\to \xR$
. Following Antipin [1], it is also possible to use a continuous gradient-projection system.We propose here an alternative method as follows:given a smooth convex function $\Phi_0: H\to \xR$ 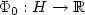 whose critical points coincidewith Sand a control parameter $\varepsilon:\xR_+\to \xR_+$
whose critical points coincidewith Sand a control parameter $\varepsilon:\xR_+\to \xR_+$ 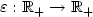 tending to zero,we consider the “Steepest Descent and Control” system \[(SDC) \qquad \dot{x}(t)+\nabla \Phi_0(x(t))+\varepsilon(t)\, \nabla \Phi_1(x(t))=0,\]
tending to zero,we consider the “Steepest Descent and Control” system \[(SDC) \qquad \dot{x}(t)+\nabla \Phi_0(x(t))+\varepsilon(t)\, \nabla \Phi_1(x(t))=0,\] 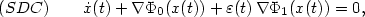 where the control ε satisfies $\int_0^{+\infty} \varepsilon(t)\, {\rm d}t =+\infty$
where the control ε satisfies $\int_0^{+\infty} \varepsilon(t)\, {\rm d}t =+\infty$ 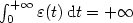 . This last condition ensures that ε “slowly” tends to 0. When H is finite dimensional, we then prove that $d(x(t), {\rm argmin}\kern 0.12em_S \Phi_1) \to 0\quad (t\to +\infty),$
. This last condition ensures that ε “slowly” tends to 0. When H is finite dimensional, we then prove that $d(x(t), {\rm argmin}\kern 0.12em_S \Phi_1) \to 0\quad (t\to +\infty),$ 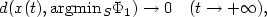 and we give sufficient conditions under which $x(t) \to \bar{x}\in \,{\rm argmin}\kern 0.12em_S \Phi_1$
and we give sufficient conditions under which $x(t) \to \bar{x}\in \,{\rm argmin}\kern 0.12em_S \Phi_1$ 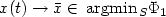 .We end the paper by numerical experiments allowing to compare the (SDC) system with the other systems already mentioned.
.We end the paper by numerical experiments allowing to compare the (SDC) system with the other systems already mentioned.