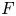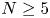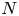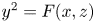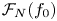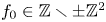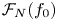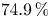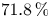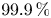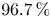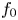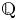Refine search
Actions for selected content:
1 results
Most odd-degree binary forms fail to primitively represent a square
- Part of
-
- Journal:
- Compositio Mathematica / Volume 160 / Issue 3 / March 2024
- Published online by Cambridge University Press:
- 08 February 2024, pp. 481-517
- Print publication:
- March 2024
-
- Article
- Export citation
-
Let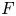
$F$ be a separable integral binary form of odd degree 
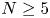$N \geq 5$. A result of Darmon and Granville known as ‘Faltings plus epsilon’ implies that the degree-
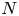$N$ superelliptic equation 
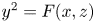$y^2 = F(x,z)$ has finitely many primitive integer solutions. In this paper, we consider the family 
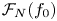$\mathscr {F}_N(f_0)$ of degree-
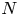$N$ superelliptic equations with fixed leading coefficient 
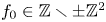$f_0 \in \mathbb {Z} \smallsetminus \pm \mathbb {Z}^2$, ordered by height. For every sufficiently large 
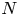$N$, we prove that among equations in the family 
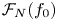$\mathscr {F}_N(f_0)$, more than 
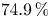$74.9\,\%$ are insoluble, and more than 
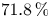$71.8\,\%$ are everywhere locally soluble but fail the Hasse principle due to the Brauer–Manin obstruction. We further show that these proportions rise to at least 
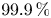$99.9\,\%$ and 
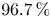$96.7\,\%$, respectively, when 
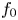$f_0$ has sufficiently many prime divisors of odd multiplicity. Our result can be viewed as a strong asymptotic form of ‘Faltings plus epsilon’ for superelliptic equations and constitutes an analogue of Bhargava's result that most hyperelliptic curves over 
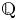$\mathbb {Q}$ have no rational points.
