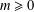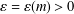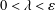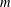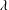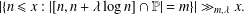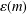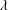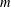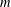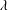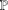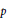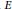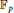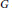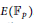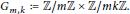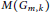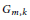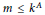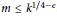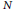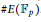We prove that for every $m\geq 0$ there exists an $\unicode[STIX]{x1D700}=\unicode[STIX]{x1D700}(m)>0$ such that if $0<\unicode[STIX]{x1D706}<\unicode[STIX]{x1D700}$ and $x$ is sufficiently large in terms of $m$ and $\unicode[STIX]{x1D706}$, then

$$\begin{eqnarray}|\{n\leq x:|[n,n+\unicode[STIX]{x1D706}\log n]\cap \mathbb{P}|=m\}|\gg _{m,\unicode[STIX]{x1D706}}x.\end{eqnarray}$$

$\unicode[STIX]{x1D700}(m)$

$\unicode[STIX]{x1D706}$

$m$

$m$

$\unicode[STIX]{x1D706}$

$x$

$\mathbb{P}$

Letting 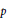$p$ vary over all primes and 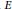$E$ vary over all elliptic curves over the finite field 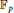${{\mathbb{F}}_{p}}$ , we study the frequency to which a given group 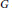$G$ arises as a group of points 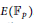$E\left( {{\mathbb{F}}_{p}} \right)$ . It is well known that the only permissible groups are of the form 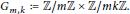${{G}_{m,\,k}}\,:=\,\mathbb{Z}\,/m\mathbb{Z}\,\times \,\mathbb{Z}/mk\mathbb{Z}$ . Given such a candidate group, we let 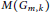$M\left( {{G}_{m,\,k}} \right)$ be the frequency to which the group 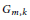${{G}_{m,\,k}}$ arises in this way. Previously, C.David and E. Smith determined an asymptotic formula for 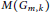$M\left( {{G}_{m,\,k}} \right)$ assuming a conjecture about primes in short arithmetic progressions. In this paper, we prove several unconditional bounds for 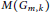$M\left( {{G}_{m,\,k}} \right)$ , pointwise and on average. In particular, we show that 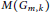$M\left( {{G}_{m,\,k}} \right)$ is bounded above by a constant multiple of the expected quantity when 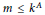$m\,\le \,{{k}^{A}}$ and that the conjectured asymptotic for 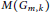$M\left( {{G}_{m,\,k}} \right)$ holds for almost all groups 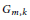${{G}_{m,\,k}}$ when 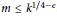$m\,\le \,{{k}^{1/4-\in }}$ . We also apply our methods to study the frequency to which a given integer 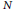$N$ arises as a group order 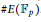$\#E\left( {{\mathbb{F}}_{p}} \right)$ .

Given an elliptic curve E and a positive integer N, we consider the problem of counting the number of primes p for which the reduction of E modulo p possesses exactly N points over 𝔽p. On average (over a family of elliptic curves), we show bounds that are significantly better than what is trivially obtained by the Hasse bound. Under some additional hypotheses, including a conjecture concerning the short-interval distribution of primes in arithmetic progressions, we obtain an asymptotic formula for the average.