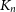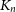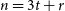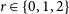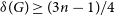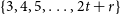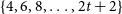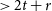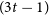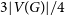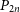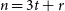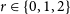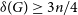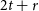A graph G arrows a graph H if in every 2-edge-colouring of G there exists a monochromatic copy of H. Schelp had the idea that if the complete graph 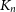$K_n$ arrows a small graph H, then every ‘dense’ subgraph of 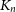$K_n$ also arrows H, and he outlined some problems in this direction. Our main result is in this spirit. We prove that for every sufficiently large n, if 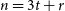$n = 3t+r$ where 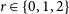$r \in \{0,1,2\}$ and G is an n-vertex graph with 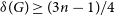$\delta(G) \ge (3n-1)/4$, then for every 2-edge-colouring of G, either there are cycles of every length 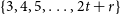$\{3, 4, 5, \dots, 2t+r\}$ of the same colour, or there are cycles of every even length 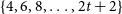$\{4, 6, 8, \dots, 2t+2\}$ of the samecolour.

Our result is tight in the sense that no longer cycles (of length 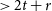$>2t+r$) can be guaranteed and the minimum degree condition cannot be reduced. It also implies the conjecture of Schelp that for every sufficiently large n, every 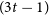$(3t-1)$-vertex graph G with minimum degree larger than 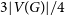$3|V(G)|/4$ arrows the path 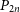$P_{2n}$ with 2n vertices. Moreover, it implies for sufficiently large n the conjecture by Benevides, Łuczak, Scott, Skokan and White that for 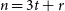$n=3t+r$ where 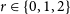$r \in \{0,1,2\}$ and every n-vertex graph G with 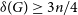$\delta(G) \ge 3n/4$, in each 2-edge-colouring of G there exists a monochromatic cycle of length at least 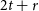$2t+r$.