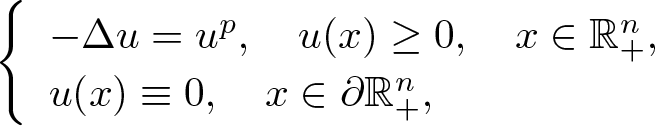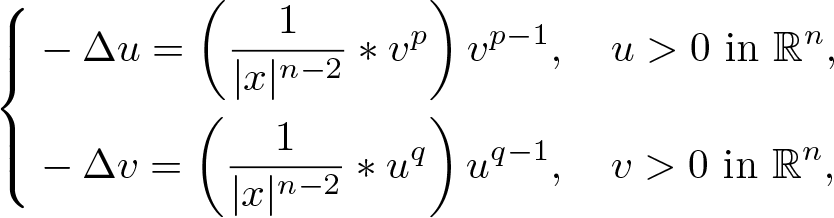Refine search
Actions for selected content:
6 results
Monotonicity of positive solutions to equations involving fractional p-Laplacian in coercive epigraph
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society , First View
- Published online by Cambridge University Press:
- 10 December 2025, pp. 1-13
-
- Article
- Export citation
Liouville theorems for the static Schrodinger equations with van der Waals type potentials
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 05 November 2025, pp. 1-27
-
- Article
- Export citation
Liouville theorems for the sub-linear Lane–Emden equation on the half space
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 18 November 2024, pp. 1-13
-
- Article
- Export citation
On Liouville theorems of a Hartree–Poisson system
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 66 / Issue 4 / November 2023
- Published online by Cambridge University Press:
- 26 October 2023, pp. 1154-1178
-
- Article
- Export citation
Nonexistence of anti-symmetric solutions for fractional Hardy–Hénon system
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 154 / Issue 3 / June 2024
- Published online by Cambridge University Press:
- 15 May 2023, pp. 862-886
- Print publication:
- June 2024
-
- Article
- Export citation
A NOTE ON RADIAL SYMMETRY FOR AN INTEGRAL EQUATION OF WOLFF TYPE
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 100 / Issue 2 / October 2019
- Published online by Cambridge University Press:
- 20 February 2019, pp. 323-327
- Print publication:
- October 2019
-
- Article
-
- You have access
- Export citation