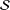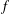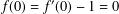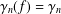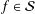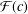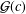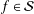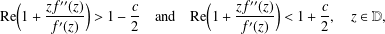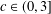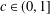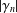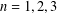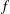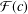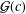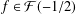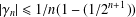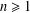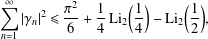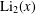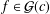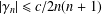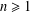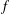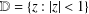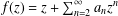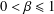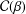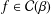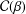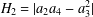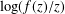Let 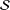 ${\mathcal{S}}$ be the family of analytic and univalent functions
${\mathcal{S}}$ be the family of analytic and univalent functions 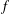 $f$ in the unit disk
$f$ in the unit disk  $\mathbb{D}$ with the normalization
$\mathbb{D}$ with the normalization 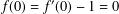 $f(0)=f^{\prime }(0)-1=0$, and let
$f(0)=f^{\prime }(0)-1=0$, and let 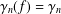 $\unicode[STIX]{x1D6FE}_{n}(f)=\unicode[STIX]{x1D6FE}_{n}$ denote the logarithmic coefficients of
$\unicode[STIX]{x1D6FE}_{n}(f)=\unicode[STIX]{x1D6FE}_{n}$ denote the logarithmic coefficients of 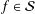 $f\in {\mathcal{S}}$. In this paper we study bounds for the logarithmic coefficients for certain subfamilies of univalent functions. Also, we consider the families
$f\in {\mathcal{S}}$. In this paper we study bounds for the logarithmic coefficients for certain subfamilies of univalent functions. Also, we consider the families 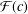 ${\mathcal{F}}(c)$ and
${\mathcal{F}}(c)$ and 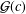 ${\mathcal{G}}(c)$ of functions
${\mathcal{G}}(c)$ of functions 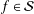 $f\in {\mathcal{S}}$ defined by
$f\in {\mathcal{S}}$ defined by 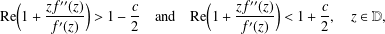 $$\begin{eqnarray}\text{Re}\biggl(1+{\displaystyle \frac{zf^{\prime \prime }(z)}{f^{\prime }(z)}}\biggr)>1-{\displaystyle \frac{c}{2}}\quad \text{and}\quad \text{Re}\biggl(1+{\displaystyle \frac{zf^{\prime \prime }(z)}{f^{\prime }(z)}}\biggr)<1+{\displaystyle \frac{c}{2}},\quad z\in \mathbb{D},\end{eqnarray}$$
$$\begin{eqnarray}\text{Re}\biggl(1+{\displaystyle \frac{zf^{\prime \prime }(z)}{f^{\prime }(z)}}\biggr)>1-{\displaystyle \frac{c}{2}}\quad \text{and}\quad \text{Re}\biggl(1+{\displaystyle \frac{zf^{\prime \prime }(z)}{f^{\prime }(z)}}\biggr)<1+{\displaystyle \frac{c}{2}},\quad z\in \mathbb{D},\end{eqnarray}$$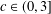 $c\in (0,3]$ and
$c\in (0,3]$ and 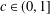 $c\in (0,1]$, respectively. We obtain the sharp upper bound for
$c\in (0,1]$, respectively. We obtain the sharp upper bound for 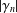 $|\unicode[STIX]{x1D6FE}_{n}|$ when
$|\unicode[STIX]{x1D6FE}_{n}|$ when 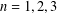 $n=1,2,3$ and
$n=1,2,3$ and 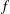 $f$ belongs to the classes
$f$ belongs to the classes 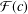 ${\mathcal{F}}(c)$ and
${\mathcal{F}}(c)$ and 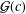 ${\mathcal{G}}(c)$, respectively. The paper concludes with the following two conjectures:
${\mathcal{G}}(c)$, respectively. The paper concludes with the following two conjectures: