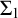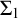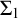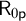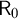Refine search
Actions for selected content:
30 results
Papers on weak first-order theories and decidability problems
- Part of
-
- Journal:
- Bulletin of Symbolic Logic / Volume 31 / Issue 4 / December 2025
- Published online by Cambridge University Press:
- 15 December 2025, p. 696
- Print publication:
- December 2025
-
- Article
-
- You have access
- Export citation
Comparison of language models for wine sentiment analysis
-
- Journal:
- Journal of Wine Economics / Volume 20 / Issue 4 / November 2025
- Published online by Cambridge University Press:
- 13 October 2025, pp. 371-384
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
7 - Features, Case and Agreement
- from Part I - Configuration and Hierarchy
-
- Book:
- Continuing Syntax
- Published online:
- 03 October 2025
- Print publication:
- 25 September 2025, pp 139-156
-
- Chapter
- Export citation
WHEN BI-INTERPRETABILITY IMPLIES SYNONYMY
- Part of
-
- Journal:
- The Review of Symbolic Logic , First View
- Published online by Cambridge University Press:
- 02 September 2025, pp. 1-20
-
- Article
-
- You have access
- Open access
- HTML
- Export citation

Machine Learning in Quantum Sciences
-
- Published online:
- 13 June 2025
- Print publication:
- 12 June 2025
3 - Phase classification
-
- Book:
- Machine Learning in Quantum Sciences
- Published online:
- 13 June 2025
- Print publication:
- 12 June 2025, pp 47-75
-
- Chapter
- Export citation
Identifying most important predictors for suicidal thoughts and behaviours among healthcare workers active during the Spain COVID-19 pandemic: a machine-learning approach
-
- Journal:
- Epidemiology and Psychiatric Sciences / Volume 34 / 2025
- Published online by Cambridge University Press:
- 08 May 2025, e28
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Feature reassembly and meso-parameters versus interpretability: From inconsistent null subjects in L1 Hebrew to no null subjects in L2 English
-
- Journal:
- Journal of Linguistics / Volume 61 / Issue 3 / August 2025
- Published online by Cambridge University Press:
- 31 January 2025, pp. 499-534
- Print publication:
- August 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On Various Causes of Improper Solutions in Maximum Likelihood Factor Analysis
-
- Journal:
- Psychometrika / Volume 43 / Issue 2 / June 1978
- Published online by Cambridge University Press:
- 01 January 2025, pp. 225-243
-
- Article
- Export citation
Generalized Structured Component Analysis Accommodating Convex Components: A Knowledge-Based Multivariate Method with Interpretable Composite Indexes
-
- Journal:
- Psychometrika / Volume 89 / Issue 1 / March 2024
- Published online by Cambridge University Press:
- 01 January 2025, pp. 241-266
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
CERTIFIED
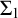 $ \Sigma _1$-SENTENCES
$ \Sigma _1$-SENTENCES
- Part of
-
- Journal:
- The Journal of Symbolic Logic , First View
- Published online by Cambridge University Press:
- 12 December 2024, pp. 1-29
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Decoder decomposition for the analysis of the latent space of nonlinear autoencoders with wind-tunnel experimental data
-
- Journal:
- Data-Centric Engineering / Volume 5 / 2024
- Published online by Cambridge University Press:
- 09 December 2024, e38
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
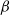 $\beta$-wave-based exploration of sensitive EEG features and classification of situation awareness
$\beta$-wave-based exploration of sensitive EEG features and classification of situation awareness
-
- Journal:
- The Aeronautical Journal / Volume 128 / Issue 1329 / November 2024
- Published online by Cambridge University Press:
- 09 May 2024, pp. 2561-2576
-
- Article
- Export citation
TREE THEORY: INTERPRETABILITY BETWEEN WEAK FIRST-ORDER THEORIES OF TREES
- Part of
-
- Journal:
- Bulletin of Symbolic Logic / Volume 29 / Issue 4 / December 2023
- Published online by Cambridge University Press:
- 10 February 2023, pp. 465-502
- Print publication:
- December 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
2 - Automating Supervision of AI Delegates
- from Part I - Foundations of Responsible AI
-
-
- Book:
- The Cambridge Handbook of Responsible Artificial Intelligence
- Published online:
- 28 October 2022
- Print publication:
- 17 November 2022, pp 19-30
-
- Chapter
-
- You have access
- Open access
- HTML
- Export citation
MUTUAL INTERPRETABILITY OF WEAK ESSENTIALLY UNDECIDABLE THEORIES
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 87 / Issue 4 / December 2022
- Published online by Cambridge University Press:
- 18 February 2022, pp. 1374-1395
- Print publication:
- December 2022
-
- Article
- Export citation
The accuracy versus interpretability trade-off in fraud detection model
-
- Journal:
- Data & Policy / Volume 3 / 2021
- Published online by Cambridge University Press:
- 05 July 2021, e12
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
THE POSET OF ALL LOGICS II: LEIBNIZ CLASSES AND HIERARCHY
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 88 / Issue 1 / March 2023
- Published online by Cambridge University Press:
- 10 June 2021, pp. 324-362
- Print publication:
- March 2023
-
- Article
- Export citation
THE POSET OF ALL LOGICS I: INTERPRETATIONS AND LATTICE STRUCTURE
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 86 / Issue 3 / September 2021
- Published online by Cambridge University Press:
- 10 June 2021, pp. 935-964
- Print publication:
- September 2021
-
- Article
- Export citation