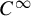Refine search
Actions for selected content:
12 results
Counting closed geodesics on rank-one manifolds without focal points
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems , First View
- Published online by Cambridge University Press:
- 03 November 2025, pp. 1-28
-
- Article
- Export citation
Approximate control of the marked length spectrum by short geodesics
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems , First View
- Published online by Cambridge University Press:
- 29 October 2025, pp. 1-24
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Sub-actions for geodesic flows on locally CAT(
 $-1$) spaces
$-1$) spaces
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 45 / Issue 12 / December 2025
- Published online by Cambridge University Press:
- 06 August 2025, pp. 3619-3662
- Print publication:
- December 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Deformational rigidity of integrable metrics on the torus
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 45 / Issue 2 / February 2025
- Published online by Cambridge University Press:
- 09 September 2024, pp. 467-503
- Print publication:
- February 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Joint partial equidistribution of Farey rays in negatively curved manifolds and trees
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 44 / Issue 9 / September 2024
- Published online by Cambridge University Press:
- 08 January 2024, pp. 2700-2736
- Print publication:
- September 2024
-
- Article
- Export citation
On the ergodicity of geodesic flows on surfaces without focal points
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 43 / Issue 12 / December 2023
- Published online by Cambridge University Press:
- 03 February 2023, pp. 4226-4248
- Print publication:
- December 2023
-
- Article
- Export citation
8 - Epilogue: A Survey of Some Techniques
-
- Book:
- Variations on a Theme of Borel
- Published online:
- 24 November 2022
- Print publication:
- 08 December 2022, pp 291-310
-
- Chapter
- Export citation
On the geodesic flow on CAT(0) spaces
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 40 / Issue 12 / December 2020
- Published online by Cambridge University Press:
- 15 August 2019, pp. 3310-3338
- Print publication:
- December 2020
-
- Article
- Export citation
Higher rank rigidity for Berwald spaces
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 40 / Issue 7 / July 2020
- Published online by Cambridge University Press:
- 18 December 2018, pp. 1991-2016
- Print publication:
- July 2020
-
- Article
- Export citation
Geodesic Flows Modelled by Expansive Flows
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 62 / Issue 1 / February 2019
- Published online by Cambridge University Press:
- 28 August 2018, pp. 61-95
-
- Article
- Export citation
Bounding Lagrangian widths via geodesic paths
- Part of
-
- Journal:
- Compositio Mathematica / Volume 150 / Issue 12 / December 2014
- Published online by Cambridge University Press:
- 17 September 2014, pp. 2143-2183
- Print publication:
- December 2014
-
- Article
- Export citation
Geodesic flow of visibility manifolds
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 77 / Issue 1 / August 2004
- Published online by Cambridge University Press:
- 09 April 2009, pp. 129-140
- Print publication:
- August 2004
-
- Article
-
- You have access
- Export citation