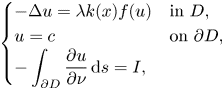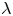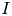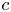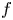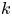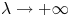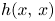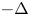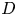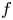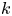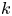Refine search
Actions for selected content:
1 results
Desingularization of 2D elliptic free-boundary problem with non-autonomous nonlinearity
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 30 April 2024, pp. 1-38
-
- Article
- Export citation
-
In this paper, we consider the existence and limiting behaviour of solutions to a semilinear elliptic equation arising from confined plasma problem in dimension two
\[ \begin{cases} -\Delta u=\lambda k(x)f(u) & \text{in}\ D,\\ u= c & \displaystyle\text{on}\ \partial D,\\ \displaystyle - \int_{\partial D} \frac{\partial u}{\partial \nu}\,{\rm d}s=I, \end{cases} \]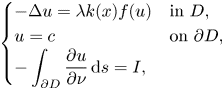where $D\subseteq \mathbb {R}^2$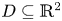
is a smooth bounded domain, $\nu$
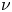is the outward unit normal to the boundary $\partial D$
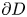, $\lambda$
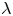and $I$
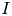are given constants and $c$
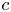is an unknown constant. Under some assumptions on $f$
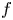and $k$
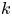, we prove that there exists a family of solutions concentrating near strict local minimum points of $\Gamma (x)=({1}/{2})h(x,\,x)- ({1}/{8\pi })\ln k(x)$
as $\lambda \to +\infty$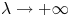
. Here $h(x,\,x)$
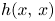is the Robin function of $-\Delta$
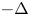in $D$
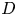. The prescribed functions $f$
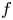and $k$
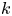can be very general. The result is proved by regarding $k$
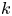as a $measure$
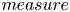and using the vorticity method, that is, solving a maximization problem for vorticity and analysing the asymptotic behaviour of maximizers. Existence of solutions concentrating near several points is also obtained.
