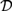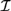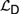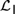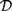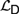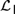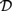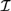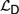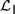Refine search
Actions for selected content:
1 results
LOGICS FOR PROPOSITIONAL DETERMINACY AND INDEPENDENCE
-
- Journal:
- The Review of Symbolic Logic / Volume 11 / Issue 3 / September 2018
- Published online by Cambridge University Press:
- 02 April 2018, pp. 470-506
- Print publication:
- September 2018
-
- Article
- Export citation
-
This paper investigates formal logics for reasoning about determinacy and independence. Propositional Dependence Logic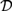
${\cal D}$ and Propositional Independence Logic 
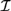${\cal I}$ are recently developed logical systems, based on team semantics, that provide a framework for such reasoning tasks. We introduce two new logics 
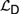${{\cal L}_D}$ and 
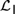${{\cal L}_{\,I\,}}$, based on Kripke semantics, and propose them as alternatives for 
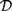${\cal D}$ and 
${\cal I}$, respectively. We analyse the relative expressive powers of these four logics and discuss the way these systems relate to natural language. We argue that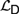 
${{\cal L}_D}$ and 
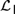${{\cal L}_{\,I\,}}$ naturally resolve a range of interpretational problems that arise in 
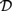${\cal D}$ and 
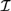${\cal I}$. We also obtain sound and complete axiomatizations for 
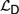${{\cal L}_D}$ and 
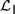${{\cal L}_{\,I\,}}$.
