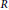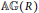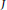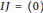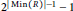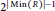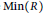We prove that the annihilating-ideal graph of a commutative semigroup with unity is, in general, not weakly perfect. This settles the conjecture of DeMeyer and Schneider [‘The annihilating-ideal graph of commutative semigroups’, J. Algebra 469 (2017), 402–420]. Further, we prove that the zero-divisor graphs of semigroups with respect to semiprime ideals are weakly perfect. This enables us to produce a large class of examples of weakly perfect zero-divisor graphs from a fixed semigroup by choosing different semiprime ideals.

We determine the metric dimension of the annihilating-ideal graph of a local finite commutative principal ring and a finite commutative principal ring with two maximal ideals. We also find bounds for the metric dimension of the annihilating-ideal graph of an arbitrary finite commutative principal ring.

In this paper, it is proved that the complement of the zero-divisor graph of a partially ordered set is weakly perfect if it has finite clique number, completely answering the question raised by Joshi and Khiste [‘Complement of the zero divisor graph of a lattice’, Bull. Aust. Math. Soc. 89 (2014), 177–190]. As a consequence, the intersection graph of an intersection-closed family of nonempty subsets of a set is weakly perfect if it has finite clique number. These results are applied to annihilating-ideal graphs and intersection graphs of submodules.

The annihilating-ideal graph of a commutative ring 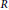$R$ , denoted by 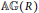$\mathbb{A}\mathbb{G}\left( R \right)$ , is a graph whose vertex set consists of all non-zero annihilating ideals and two distinct vertices $I$ and 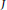$J$ are adjacent if and only if 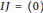$IJ\,=\,\left( 0 \right)$ . Here we show that if 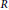$R$ is a reduced ring and the independence number of 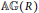$\mathbb{A}\mathbb{G}\left( R \right)$ is finite, then the edge chromatic number of 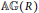$\mathbb{A}\mathbb{G}\left( R \right)$ equals its maximum degree and this number equals 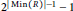${{2}^{\left| \min \left( R \right) \right|-1}}-\,1$ ; also, it is proved that the independence number of 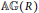$\mathbb{A}\mathbb{G}\left( R \right)$ equals 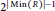${{2}^{\left| \min \left( R \right) \right|-1}}$ , where 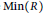$\min \left( R \right)$ denotes the set of minimal prime ideals of 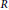$R$ . Then we give some criteria for a graph to be isomorphic with an annihilating-ideal graph of a ring. For example, it is shown that every bipartite annihilating-ideal graph is a complete bipartite graph with at most two horns. Among other results, it is shown that a finite graph 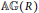$\mathbb{A}\mathbb{G}\left( R \right)$ is not Eulerian, and that it is Hamiltonian if and only if 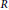$R$ contains no Gorenstain ring as its direct summand.