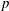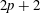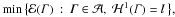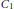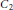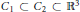Refine search
Actions for selected content:
32 results
Optimal free export/import regions
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 64 / Issue 4 / December 2021
- Published online by Cambridge University Press:
- 17 September 2020, pp. 737-751
- Print publication:
- December 2021
-
- Article
- Export citation
The Steklov Problem on Differential Forms
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 71 / Issue 2 / April 2019
- Published online by Cambridge University Press:
- 07 January 2019, pp. 417-435
- Print publication:
- April 2019
-
- Article
-
- You have access
- Export citation
Reverse Faber–Krahn and Mahler inequalities for the Cheeger constant
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 148 / Issue 5 / October 2018
- Published online by Cambridge University Press:
- 22 June 2018, pp. 913-937
- Print publication:
- October 2018
-
- Article
- Export citation
An eigenvalue optimization problem for the p-Laplacian
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 145 / Issue 6 / December 2015
- Published online by Cambridge University Press:
- 08 October 2015, pp. 1145-1151
- Print publication:
- December 2015
-
- Article
- Export citation
Minimising convex combinations of low eigenvalues∗
-
- Journal:
- ESAIM: Control, Optimisation and Calculus of Variations / Volume 20 / Issue 2 / April 2014
- Published online by Cambridge University Press:
- 07 March 2014, pp. 442-459
- Print publication:
- April 2014
-
- Article
- Export citation
Global minimizer of the ground state for two phase conductorsin low contrast regime∗∗∗
-
- Journal:
- ESAIM: Control, Optimisation and Calculus of Variations / Volume 20 / Issue 2 / April 2014
- Published online by Cambridge University Press:
- 03 March 2014, pp. 362-388
- Print publication:
- April 2014
-
- Article
- Export citation
A priori error estimates for finite elementdiscretizations of a shape optimization problem
-
- Journal:
- ESAIM: Mathematical Modelling and Numerical Analysis / Volume 47 / Issue 6 / November 2013
- Published online by Cambridge University Press:
- 07 October 2013, pp. 1733-1763
- Print publication:
- November 2013
-
- Article
- Export citation
Shape optimization problems for metric graphs
-
- Journal:
- ESAIM: Control, Optimisation and Calculus of Variations / Volume 20 / Issue 1 / January 2014
- Published online by Cambridge University Press:
- 29 August 2013, pp. 1-22
- Print publication:
- January 2014
-
- Article
- Export citation
Boundary control and shape optimization for the robust designof bypass anastomoses under uncertainty
-
- Journal:
- ESAIM: Mathematical Modelling and Numerical Analysis / Volume 47 / Issue 4 / July 2013
- Published online by Cambridge University Press:
- 17 June 2013, pp. 1107-1131
- Print publication:
- July 2013
-
- Article
- Export citation
Convex shape optimization for the least biharmonic Stekloveigenvalue
-
- Journal:
- ESAIM: Control, Optimisation and Calculus of Variations / Volume 19 / Issue 2 / April 2013
- Published online by Cambridge University Press:
- 10 January 2013, pp. 385-403
- Print publication:
- April 2013
-
- Article
- Export citation
Optimal Roughening of Convex Bodies
-
- Journal:
- Canadian Journal of Mathematics / Volume 64 / Issue 5 / 01 October 2012
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1058-1074
- Print publication:
- 01 October 2012
-
- Article
-
- You have access
- Export citation
Adaptive finite element method for shape optimization∗
-
- Journal:
- ESAIM: Control, Optimisation and Calculus of Variations / Volume 18 / Issue 4 / October 2012
- Published online by Cambridge University Press:
- 16 January 2012, pp. 1122-1149
- Print publication:
- October 2012
-
- Article
- Export citation
On convex sets that minimize the averagedistance
-
- Journal:
- ESAIM: Control, Optimisation and Calculus of Variations / Volume 18 / Issue 4 / October 2012
- Published online by Cambridge University Press:
- 16 January 2012, pp. 1049-1072
- Print publication:
- October 2012
-
- Article
- Export citation
Optimisation de forme des structures hyperélastiques incompressibles et anisotropes
-
- Journal:
- Mechanics & Industry / Volume 12 / Issue 4 / 2011
- Published online by Cambridge University Press:
- 25 August 2011, pp. 293-300
- Print publication:
- 2011
-
- Article
- Export citation
A phase-field model for compliance shape optimization in nonlinear elasticity
-
- Journal:
- ESAIM: Control, Optimisation and Calculus of Variations / Volume 18 / Issue 1 / January 2012
- Published online by Cambridge University Press:
- 23 December 2010, pp. 229-258
- Print publication:
- January 2012
-
- Article
- Export citation
On a Bernoulli problem with geometric constraints
-
- Journal:
- ESAIM: Control, Optimisation and Calculus of Variations / Volume 18 / Issue 1 / January 2012
- Published online by Cambridge University Press:
- 02 December 2010, pp. 157-180
- Print publication:
- January 2012
-
- Article
- Export citation
On the ersatz material approximation in level-set methods
-
- Journal:
- ESAIM: Control, Optimisation and Calculus of Variations / Volume 16 / Issue 3 / July 2010
- Published online by Cambridge University Press:
- 31 July 2009, pp. 618-634
- Print publication:
- July 2010
-
- Article
- Export citation
The squares of the Laplacian-Dirichlet eigenfunctionsare generically linearly independent
-
- Journal:
- ESAIM: Control, Optimisation and Calculus of Variations / Volume 16 / Issue 3 / July 2010
- Published online by Cambridge University Press:
- 02 July 2009, pp. 794-805
- Print publication:
- July 2010
-
- Article
- Export citation
Optimal measures for the fundamental gapof Schrödinger operators
-
- Journal:
- ESAIM: Control, Optimisation and Calculus of Variations / Volume 16 / Issue 1 / January 2010
- Published online by Cambridge University Press:
- 19 December 2008, pp. 194-205
- Print publication:
- January 2010
-
- Article
- Export citation
SYMMETRY RESULT FOR SOME OVERDETERMINED VALUE PROBLEMS
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 49 / Issue 4 / April 2008
- Published online by Cambridge University Press:
- 01 April 2008, pp. 479-494
-
- Article
-
- You have access
- Export citation