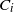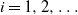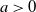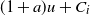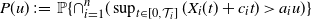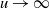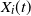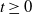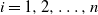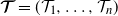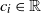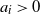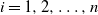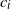Refine search
Actions for selected content:
97 results
Asymptotics for a multidimensional risk model with a random number of delayed claims and multivariate regularly varying distribution
- Part of
-
- Journal:
- Advances in Applied Probability , First View
- Published online by Cambridge University Press:
- 10 December 2025, pp. 1-30
-
- Article
- Export citation
A new approach in two-dimensional heavy-tailed distributions
-
- Journal:
- Annals of Actuarial Science / Volume 19 / Issue 2 / July 2025
- Published online by Cambridge University Press:
- 09 May 2025, pp. 317-349
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Bankruptcy probabilities under non-poisson inspection
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 57 / Issue 4 / December 2025
- Published online by Cambridge University Press:
- 19 March 2025, pp. 1281-1320
- Print publication:
- December 2025
-
- Article
- Export citation
On dual risk models with proportional gains and dependencies
-
- Journal:
- Probability in the Engineering and Informational Sciences / Volume 39 / Issue 2 / April 2025
- Published online by Cambridge University Press:
- 23 December 2024, pp. 156-187
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A singularly perturbed ruin problem for a two-dimensional Brownian motion in the positive quadrant
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 62 / Issue 1 / March 2025
- Published online by Cambridge University Press:
- 14 October 2024, pp. 269-283
- Print publication:
- March 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Multivariate regularly varying insurance and financial risks in multidimensional risk models
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 61 / Issue 4 / December 2024
- Published online by Cambridge University Press:
- 13 May 2024, pp. 1319-1342
- Print publication:
- December 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On the joint survival probability of two collaborating firms
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 61 / Issue 2 / June 2024
- Published online by Cambridge University Press:
- 01 August 2023, pp. 369-384
- Print publication:
- June 2024
-
- Article
- Export citation
A dual risk model with additive and proportional gains: ruin probability and dividends
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 55 / Issue 2 / June 2023
- Published online by Cambridge University Press:
- 08 February 2023, pp. 549-580
- Print publication:
- June 2023
-
- Article
- Export citation
Extrema of multi-dimensional Gaussian processes over random intervals
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 59 / Issue 1 / March 2022
- Published online by Cambridge University Press:
- 28 February 2022, pp. 81-104
- Print publication:
- March 2022
-
- Article
- Export citation
A transient Cramér–Lundberg model with applications to credit risk
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 58 / Issue 3 / September 2021
- Published online by Cambridge University Press:
- 16 September 2021, pp. 721-745
- Print publication:
- September 2021
-
- Article
- Export citation
RUIN PROBABILITIES FOR A MULTIDIMENSIONAL RISK MODEL WITH NON-STATIONARY ARRIVALS AND SUBEXPONENTIAL CLAIMS
-
- Journal:
- Probability in the Engineering and Informational Sciences / Volume 36 / Issue 3 / July 2022
- Published online by Cambridge University Press:
- 16 March 2021, pp. 799-811
-
- Article
- Export citation
Exponential convergence rate of ruin probabilities for level-dependent Lévy-driven risk processes
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 56 / Issue 4 / December 2019
- Published online by Cambridge University Press:
- 11 December 2019, pp. 1244-1268
- Print publication:
- December 2019
-
- Article
- Export citation
The De Vylder–Goovaerts conjecture holds within the diffusion limit
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 56 / Issue 2 / June 2019
- Published online by Cambridge University Press:
- 30 July 2019, pp. 546-557
- Print publication:
- June 2019
-
- Article
- Export citation
A PARTICULAR BIDIMENSIONAL TIME-DEPENDENT RENEWAL RISK MODEL WITH CONSTANT INTEREST RATES
-
- Journal:
- Probability in the Engineering and Informational Sciences / Volume 34 / Issue 2 / April 2020
- Published online by Cambridge University Press:
- 07 March 2019, pp. 172-182
-
- Article
-
- You have access
- Export citation
Asymptotic expansions and saddlepoint approximations using the analytic continuation of moment generating functions
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 56 / Issue 1 / March 2019
- Published online by Cambridge University Press:
- 12 July 2019, pp. 307-338
- Print publication:
- March 2019
-
- Article
- Export citation
An identity based on the generalised negative binomial distribution with applications in ruin theory
-
- Journal:
- Annals of Actuarial Science / Volume 13 / Issue 2 / September 2019
- Published online by Cambridge University Press:
- 10 September 2018, pp. 308-319
-
- Article
- Export citation
Ruin probabilities in a Sparre Andersen model with dependency structure based on a threshold window
-
- Journal:
- Annals of Actuarial Science / Volume 12 / Issue 2 / September 2018
- Published online by Cambridge University Press:
- 08 November 2017, pp. 269-295
-
- Article
- Export citation
Asymptotic tail behaviour of phase-type scale mixture distributions
-
- Journal:
- Annals of Actuarial Science / Volume 12 / Issue 2 / September 2018
- Published online by Cambridge University Press:
- 29 August 2017, pp. 412-432
-
- Article
- Export citation
MEASURING THE IMPACT OF A BONUS-MALUS SYSTEM IN FINITE AND CONTINUOUS TIME RUIN PROBABILITIES FOR LARGE PORTFOLIOS IN MOTOR INSURANCE
-
- Journal:
- ASTIN Bulletin: The Journal of the IAA / Volume 47 / Issue 2 / May 2017
- Published online by Cambridge University Press:
- 21 March 2017, pp. 417-435
- Print publication:
- May 2017
-
- Article
- Export citation
On the central management of risk networks
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 49 / Issue 1 / March 2017
- Published online by Cambridge University Press:
- 17 March 2017, pp. 221-237
- Print publication:
- March 2017
-
- Article
-
- You have access
- Export citation