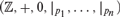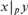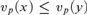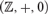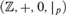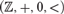Refine search
Actions for selected content:
6 results
UNDEFINABILITY OF MULTIPLICATION IN PRESBURGER ARITHMETIC WITH SETS OF POWERS
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 90 / Issue 2 / June 2025
- Published online by Cambridge University Press:
- 10 October 2023, pp. 872-886
- Print publication:
- June 2025
-
- Article
- Export citation
A NEW DP-MINIMAL EXPANSION OF THE INTEGERS
-
- Journal:
- The Journal of Symbolic Logic / Volume 84 / Issue 2 / June 2019
- Published online by Cambridge University Press:
- 04 March 2019, pp. 632-663
- Print publication:
- June 2019
-
- Article
- Export citation
THERE ARE NO INTERMEDIATE STRUCTURES BETWEEN THE GROUP OF INTEGERS AND PRESBURGER ARITHMETIC
-
- Journal:
- The Journal of Symbolic Logic / Volume 83 / Issue 1 / March 2018
- Published online by Cambridge University Press:
- 01 May 2018, pp. 187-207
- Print publication:
- March 2018
-
- Article
- Export citation
PRESBURGER ARITHMETIC, RATIONAL GENERATING FUNCTIONS, AND QUASI-POLYNOMIALS
-
- Journal:
- The Journal of Symbolic Logic / Volume 80 / Issue 2 / June 2015
- Published online by Cambridge University Press:
- 22 April 2015, pp. 433-449
- Print publication:
- June 2015
-
- Article
- Export citation
Deciding whether a relation defined inPresburger logiccan be defined in weaker logics
-
- Journal:
- RAIRO - Theoretical Informatics and Applications / Volume 42 / Issue 1 / January 2008
- Published online by Cambridge University Press:
- 18 January 2008, pp. 121-135
- Print publication:
- January 2008
-
- Article
- Export citation
Presburger sets and p-minimal fields
-
- Journal:
- The Journal of Symbolic Logic / Volume 68 / Issue 1 / March 2003
- Published online by Cambridge University Press:
- 12 March 2014, pp. 153-162
- Print publication:
- March 2003
-
- Article
- Export citation