Refine search
Actions for selected content:
8 results
Non-parametric Regression Among Factor Scores: Motivation and Diagnostics for Nonlinear Structural Equation Models
-
- Journal:
- Psychometrika / Volume 89 / Issue 3 / September 2024
- Published online by Cambridge University Press:
- 01 January 2025, pp. 822-850
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
SOFTWARE RELIABILITY BASED ON RENEWAL PROCESS MODELING FOR ERROR OCCURRENCE DUE TO EACH BUG WITH PERIODIC DEBUGGING SCHEDULE
-
- Journal:
- Probability in the Engineering and Informational Sciences / Volume 36 / Issue 1 / January 2022
- Published online by Cambridge University Press:
- 02 June 2020, pp. 87-104
-
- Article
- Export citation
Non-parametric estimation for a pure-jump Lévy process
-
- Journal:
- Annals of Actuarial Science / Volume 12 / Issue 2 / September 2018
- Published online by Cambridge University Press:
- 10 May 2017, pp. 338-349
-
- Article
- Export citation
COMPOSITE BERNSTEIN COPULAS
-
- Journal:
- ASTIN Bulletin: The Journal of the IAA / Volume 45 / Issue 2 / May 2015
- Published online by Cambridge University Press:
- 11 March 2015, pp. 445-475
- Print publication:
- May 2015
-
- Article
- Export citation
Using Mixed Poisson Processes in Connection with Bonus-Malus Systems1
-
- Journal:
- ASTIN Bulletin: The Journal of the IAA / Volume 29 / Issue 1 / May 1999
- Published online by Cambridge University Press:
- 29 August 2014, pp. 81-99
- Print publication:
- May 1999
-
- Article
-
- You have access
- Export citation
Estimating the reduced moments of a random measure
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 31 / Issue 1 / March 1999
- Published online by Cambridge University Press:
- 01 July 2016, pp. 48-62
- Print publication:
- March 1999
-
- Article
- Export citation
Confidence bounds for the adjustment coefficient
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 28 / Issue 3 / September 1996
- Published online by Cambridge University Press:
- 01 July 2016, pp. 802-827
- Print publication:
- September 1996
-
- Article
- Export citation
Convergence rate of perturbed empirical distribution functions
-
- Journal:
- Journal of Applied Probability / Volume 16 / Issue 1 / March 1979
- Published online by Cambridge University Press:
- 14 July 2016, pp. 163-173
- Print publication:
- March 1979
-
- Article
- Export citation
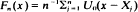 where
where 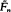 , is obtained if
, is obtained if 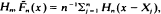 , where
, where 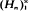 is a sequence of d.f.'s converging weakly to
is a sequence of d.f.'s converging weakly to 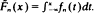 . It is shown that if F satisfies some smoothness conditions and the perturbation is not too drastic then
. It is shown that if F satisfies some smoothness conditions and the perturbation is not too drastic then 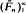 ‘has the Chung–Smirnov property'; i.e., with probability one,
‘has the Chung–Smirnov property'; i.e., with probability one, 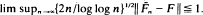 1. But if the perturbation is too vigorous then this property is lost: e.g., if F is the uniform distribution and
1. But if the perturbation is too vigorous then this property is lost: e.g., if F is the uniform distribution and 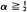 or
or