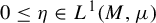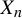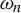We study quasi-stationary distributions and quasi-limiting behaviour of Markov chains in general reducible state spaces with absorption. First, we consider state spaces that can be decomposed into two successive subsets (with communication possible in a single direction), differentiating between three situations, and characterize the exponential order of magnitude and the exact polynomial correction, called the polynomial convergence parameter, for the leading-order term of the semigroup for large time. Second, we consider general Markov chains with finitely or countably many communication classes by applying the first results iteratively over the communication classes of the chain. We conclude with an application of these results to the case of denumerable state spaces, where we prove existence for a quasi-stationary distribution without assuming irreducibility before absorption, but only aperiodicity, existence of a Lyapunov function, and existence of a point with almost surely finite return time.

In this paper, we consider absorbing Markov chains $X_n$ admitting a quasi-stationary measure $\mu $ on M where the transition kernel ${\mathcal P}$ admits an eigenfunction $0\leq \eta \in L^1(M,\mu )$. We find conditions on the transition densities of ${\mathcal P}$ with respect to $\mu $ which ensure that $\eta (x) \mu (\mathrm {d} x)$ is a quasi-ergodic measure for $X_n$ and that the Yaglom limit converges to the quasi-stationary measure $\mu $-almost surely. We apply this result to the random logistic map $X_{n+1} = \omega _n X_n (1-X_n)$ absorbed at ${\mathbb R} \setminus [0,1],$ where $\omega _n$ is an independent and identically distributed sequence of random variables uniformly distributed in $[a,b],$ for $1\leq a <4$ and $b>4.$