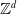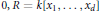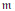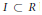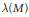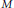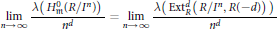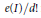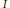Refine search
Actions for selected content:
21 results
Discrete-to-continuum limits of optimal transport with linear growth on periodic graphs
-
- Journal:
- European Journal of Applied Mathematics , First View
- Published online by Cambridge University Press:
- 20 December 2024, pp. 1-29
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Associations of linear growth and weight gain in the first 2 years with bone mass at 4 years of age in children in Dhaka, Bangladesh
-
- Journal:
- Public Health Nutrition / Volume 27 / Issue 1 / 2024
- Published online by Cambridge University Press:
- 22 November 2024, e265
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Trends and long-term variation explaining nutritional determinants of child linear growth: analysis of Bangladesh Demographic and Health Surveys 1996–2018
-
- Journal:
- Public Health Nutrition / Volume 26 / Issue 12 / December 2023
- Published online by Cambridge University Press:
- 27 October 2023, pp. 2758-2770
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Associations between maternal and infant selenium status and child growth in a birth cohort from Dhaka, Bangladesh
-
- Journal:
- British Journal of Nutrition / Volume 130 / Issue 9 / 14 November 2023
- Published online by Cambridge University Press:
- 22 March 2023, pp. 1558-1572
- Print publication:
- 14 November 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Vitamin B12 and/or folic acid supplementation on linear growth: a 6-year follow-up study of a randomised controlled trial in early childhood in North India
-
- Journal:
- British Journal of Nutrition / Volume 129 / Issue 7 / 14 April 2023
- Published online by Cambridge University Press:
- 25 July 2022, pp. 1172-1179
- Print publication:
- 14 April 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Association of serum PUFA and linear growth over 12 months among 6–10 years old Ugandan children with or without HIV
-
- Journal:
- Public Health Nutrition / Volume 25 / Issue 5 / May 2022
- Published online by Cambridge University Press:
- 04 April 2022, pp. 1194-1204
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Exposure to aflatoxins and fumonisins and linear growth of children in rural Ethiopia: a longitudinal study
-
- Journal:
- Public Health Nutrition / Volume 24 / Issue 12 / August 2021
- Published online by Cambridge University Press:
- 01 February 2021, pp. 3662-3673
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A macro- and micronutrient-fortified complementary food supplement reduced acute infection, improved haemoglobin and showed a dose–response effect in improving linear growth: a 12-month cluster randomised trial
-
- Journal:
- Journal of Nutritional Science / Volume 8 / 2019
- Published online by Cambridge University Press:
- 27 June 2019, e22
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The role of offspring’s birthweight on the association between pre-pregnancy obesity and offspring’s childhood anthropometrics: a mediation analysis
-
- Journal:
- Journal of Developmental Origins of Health and Disease / Volume 10 / Issue 5 / October 2019
- Published online by Cambridge University Press:
- 10 January 2019, pp. 570-577
-
- Article
- Export citation
Environmental enteric dysfunction and systemic inflammation predict reduced weight but not length gain in rural Bangladeshi children
-
- Journal:
- British Journal of Nutrition / Volume 119 / Issue 4 / 28 February 2018
- Published online by Cambridge University Press:
- 02 March 2018, pp. 407-414
- Print publication:
- 28 February 2018
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The relationships among iron supplement use, Hb concentration and linear growth in young children: Ethiopian Demographic and Health Survey
-
- Journal:
- British Journal of Nutrition / Volume 118 / Issue 9 / 14 November 2017
- Published online by Cambridge University Press:
- 29 November 2017, pp. 730-736
- Print publication:
- 14 November 2017
-
- Article
-
- You have access
- HTML
- Export citation
Trends and drivers of Macoma balthica L. dynamics in Kandalaksha Bay, the White Sea
-
- Journal:
- Journal of the Marine Biological Association of the United Kingdom / Volume 98 / Issue 1 / February 2018
- Published online by Cambridge University Press:
- 22 August 2017, pp. 13-24
-
- Article
- Export citation
Differential effects of dietary diversity and maternal characteristics on linear growth of children aged 6–59 months in sub-Saharan Africa: a multi-country analysis
-
- Journal:
- Public Health Nutrition / Volume 20 / Issue 6 / April 2017
- Published online by Cambridge University Press:
- 09 January 2017, pp. 1029-1045
-
- Article
-
- You have access
- HTML
- Export citation
Dietary diversity, animal source food consumption and linear growth among children aged 1–5 years in Bandung, Indonesia: a longitudinal observational study
-
- Journal:
- British Journal of Nutrition / Volume 116 / Issue S1 / July 2016
- Published online by Cambridge University Press:
- 28 January 2016, pp. S27-S35
- Print publication:
- July 2016
-
- Article
-
- You have access
- HTML
- Export citation
Stunting at birth: recognition of early-life linear growth failure in the western highlands of Guatemala
-
- Journal:
- Public Health Nutrition / Volume 18 / Issue 10 / July 2015
- Published online by Cambridge University Press:
- 27 November 2014, pp. 1737-1745
-
- Article
-
- You have access
- HTML
- Export citation
Complementary feeding and attained linear growth among 6–23-month-old children
-
- Journal:
- Public Health Nutrition / Volume 17 / Issue 9 / September 2014
- Published online by Cambridge University Press:
- 19 September 2013, pp. 1975-1983
-
- Article
-
- You have access
- HTML
- Export citation
Dietary arginine and linear growth: the Copenhagen School Child Intervention Study
-
- Journal:
- British Journal of Nutrition / Volume 109 / Issue 6 / 28 March 2013
- Published online by Cambridge University Press:
- 10 October 2012, pp. 1031-1039
- Print publication:
- 28 March 2013
-
- Article
-
- You have access
- HTML
- Export citation
Accelerated growth without prepubertal obesity in nutritionally programmed microswine offspring
-
- Journal:
- Journal of Developmental Origins of Health and Disease / Volume 3 / Issue 2 / April 2012
- Published online by Cambridge University Press:
- 17 February 2012, pp. 92-102
-
- Article
- Export citation
Asymptotic Behavior of the Length of Local Cohomology
-
- Journal:
- Canadian Journal of Mathematics / Volume 57 / Issue 6 / 01 December 2005
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1178-1192
- Print publication:
- 01 December 2005
-
- Article
-
- You have access
- Export citation
Linear and knemometric growth in the early phase of rehabilitation from severe malnutrition
-
- Journal:
- British Journal of Nutrition / Volume 85 / Issue 6 / May 2001
- Published online by Cambridge University Press:
- 09 March 2007, pp. 755-759
- Print publication:
- May 2001
-
- Article
-
- You have access
- Export citation