Refine search
Actions for selected content:
6 results
The Markov chain embedding problem in a one-jump setting
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 62 / Issue 2 / June 2025
- Published online by Cambridge University Press:
- 09 December 2024, pp. 674-696
- Print publication:
- June 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On equal-input and monotone Markov matrices
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 54 / Issue 2 / June 2022
- Published online by Cambridge University Press:
- 06 June 2022, pp. 460-492
- Print publication:
- June 2022
-
- Article
- Export citation
Continuous flows generate few homeomorphisms
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 63 / Issue 4 / November 2020
- Published online by Cambridge University Press:
- 25 August 2020, pp. 971-983
-
- Article
- Export citation
On the family of affine threefolds
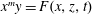 $\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}x^m y= F(x, z, t)$
$\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}x^m y= F(x, z, t)$
- Part of
-
- Journal:
- Compositio Mathematica / Volume 150 / Issue 6 / June 2014
- Published online by Cambridge University Press:
- 09 June 2014, pp. 979-998
- Print publication:
- June 2014
-
- Article
- Export citation
On the Embedding Problem for Discrete-Time Markov Chains
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 50 / Issue 4 / December 2013
- Published online by Cambridge University Press:
- 30 January 2018, pp. 918-930
- Print publication:
- December 2013
-
- Article
-
- You have access
- Export citation
Modelling hierarchical systems by a continuous-time homogeneous Markov chain using two-wave panel data
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 36 / Issue 3 / September 1999
- Published online by Cambridge University Press:
- 14 July 2016, pp. 644-653
- Print publication:
- September 1999
-
- Article
- Export citation











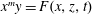
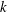
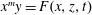
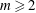
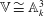
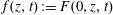
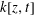
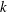
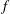
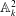
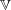
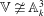
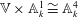
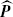 cannot be written as an exponential of an infinitesimal generator
cannot be written as an exponential of an infinitesimal generator 