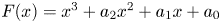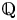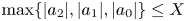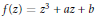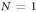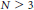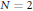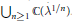Refine search
Actions for selected content:
5 results
Lavaurs algorithm for cubic symmetric polynomials
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 45 / Issue 8 / August 2025
- Published online by Cambridge University Press:
- 06 January 2025, pp. 2314-2340
- Print publication:
- August 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On monic abelian cubics
- Part of
-
- Journal:
- Compositio Mathematica / Volume 158 / Issue 3 / March 2022
- Published online by Cambridge University Press:
- 16 May 2022, pp. 550-567
- Print publication:
- March 2022
-
- Article
- Export citation
Cubic Polynomials with Periodic Cycles of a Specified Multiplier
-
- Journal:
- Canadian Journal of Mathematics / Volume 64 / Issue 2 / 16 April 2012
- Published online by Cambridge University Press:
- 20 November 2018, pp. 318-344
- Print publication:
- 16 April 2012
-
- Article
-
- You have access
- Export citation
NONLINEAR ERROR CORRECTION: THE CASE OF MONEY DEMAND IN THE UNITED KINGDOM (1878–2000)
-
- Journal:
- Macroeconomic Dynamics / Volume 8 / Issue 1 / February 2004
- Published online by Cambridge University Press:
- 30 January 2004, pp. 76-116
-
- Article
- Export citation