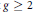Let 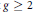$g\,\ge \,2$ . A real number is said to be $g$ -normal if its base $g$ expansion contains every finite sequence of digits with the expected limiting frequency. Let $\varphi$ denote Euler’s totient function, let $\sigma$ be the sum-of-divisors function, and let $\lambda$ be Carmichael’s lambda-function. We show that if 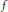$f$ is any function formed by composing $\varphi$ , $\sigma$ , or $\lambda$ , then the number

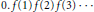$$0.f\left( 1 \right)f\left( 2 \right)f\left( 3 \right)\,.\,.\,.$$

obtained by concatenating the base $g$ digits of successive 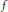$f$ -values is $g$ -normal. We also prove the same result if the inputs 1,2,3....are replaced with the primes 2, 3, 5.... The proof is an adaptation of a method introduced by Copeland and Erdõs in 1946 to prove the 10-normality of 0:235711131719...

Let $g\geqslant 2$. A real number is said to be $g$-normal if its base $g$ expansion contains every finite sequence of digits with the expected limiting frequency. Let $\unicode[STIX]{x1D711}$ denote Euler’s totient function, let $\unicode[STIX]{x1D70E}$ be the sum-of-divisors function, and let $\unicode[STIX]{x1D706}$ be Carmichael’s lambda-function. We show that if $f$ is any function formed by composing $\unicode[STIX]{x1D711}$, $\unicode[STIX]{x1D70E}$, or $\unicode[STIX]{x1D706}$, then the number

$$\begin{eqnarray}0.f(1)f(2)f(3)\cdots\end{eqnarray}$$

$g$

$f$

$g$

$1,2,3,\ldots$

$2,3,5,\ldots$

$0.235711131719\cdots \,$