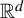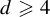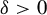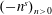Refine search
Actions for selected content:
11 results
On the dimension theory of Okamoto’s function
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 14 November 2025, pp. 1-27
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Slices of the Takagi function
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 44 / Issue 9 / September 2024
- Published online by Cambridge University Press:
- 20 December 2023, pp. 2361-2398
- Print publication:
- September 2024
-
- Article
- Export citation
The Assouad dimension of self-affine measures on sponges
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 43 / Issue 9 / September 2023
- Published online by Cambridge University Press:
- 08 September 2022, pp. 2974-2996
- Print publication:
- September 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Hausdorff measure and Assouad dimension of generic self-conformal IFS on the line
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 151 / Issue 6 / December 2021
- Published online by Cambridge University Press:
- 15 December 2020, pp. 2051-2081
- Print publication:
- December 2021
-
- Article
- Export citation
2 - The Assouad Dimension
- from Part One - Theory
-
- Book:
- Assouad Dimension and Fractal Geometry
- Published online:
- 13 October 2020
- Print publication:
- 29 October 2020, pp 10-21
-
- Chapter
- Export citation

Assouad Dimension and Fractal Geometry
-
- Published online:
- 13 October 2020
- Print publication:
- 29 October 2020
Assouad Spectrum Thresholds for Some Random Constructions
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 63 / Issue 2 / June 2020
- Published online by Cambridge University Press:
- 12 December 2019, pp. 434-453
- Print publication:
- June 2020
-
- Article
-
- You have access
- Export citation
Expansions of the Real Field by Canonical Products
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 63 / Issue 3 / September 2020
- Published online by Cambridge University Press:
- 04 October 2019, pp. 506-521
- Print publication:
- September 2020
-
- Article
-
- You have access
- Export citation
The quasi-Assouad dimension of stochastically self-similar sets
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 150 / Issue 1 / February 2020
- Published online by Cambridge University Press:
- 24 January 2019, pp. 261-275
- Print publication:
- February 2020
-
- Article
- Export citation
Assouad Dimension of Random Processes
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 62 / Issue 1 / February 2019
- Published online by Cambridge University Press:
- 16 November 2018, pp. 281-290
-
- Article
- Export citation
Assouad dimensions of complementary sets
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 148 / Issue 3 / June 2018
- Published online by Cambridge University Press:
- 12 April 2018, pp. 517-540
- Print publication:
- June 2018
-
- Article
- Export citation