Hostname: page-component-68c7f8b79f-s5tvr Total loading time: 0 Render date: 2026-01-13T23:30:38.498Z Has data issue: false hasContentIssue false
  • English
  • Français

The Schur–Weyl duality and invariants for classical Lie superalgebras

Part of: Representation theory of groups Lie algebras and Lie superalgebras

Published online by Cambridge University Press:  27 November 2025

Yang Luo  and
Yongjie Wang
Yang Luo
Affiliation:
College of Science, National University of Defense Technology , China e-mail: yangluo@mail.ustc.edu.cn
Yongjie Wang*
Affiliation:
School of Mathematics, Hefei University of Technology , China
*
e-mail: wyjie@mail.ustc.edu.cn
Get access Rights & Permissions [Opens in a new window]

Abstract

In this article, we provide a specific characterization of invariants of classical Lie superalgebras from the super-analog of the Schur–Weyl duality in a unified way. We establish 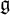$\mathfrak {g}$-invariants of the tensor algebra 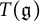$T(\mathfrak {g})$, the supersymmetric algebra 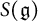$S(\mathfrak {g})$, and the universal enveloping algebra 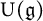$\mathrm {U}(\mathfrak {g})$ of a classical Lie superalgebra 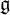$\mathfrak {g}$ corresponding to every element in centralizer algebras and their relationship under supersymmetrization. As a byproduct, we prove that the restriction on 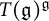$T(\mathfrak {g})^{\mathfrak {g}}$ of the projection from 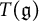$T(\mathfrak {g})$ to 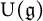$\mathrm {U}(\mathfrak {g})$ is surjective, which enables us to determine the generators of the center 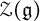$\mathcal {Z}(\mathfrak {g})$ except for 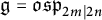$\mathfrak {g}=\mathfrak {osp}_{2m|2n}$. Additionally, we present an alternative algebraic proof of the triviality of 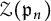$\mathcal {Z}(\mathfrak {p}_n)$. The key ingredient involves a technique lemma related to the symmetric group and Brauer diagrams.

Keywords

Classical Lie superalgebrasBrauer diagramCasimir elementsGelfand invariantsSchur–Weyl duality

MSC classification

Primary: 17B35: Universal enveloping (super)algebras 17B10: Representations, algebraic theory (weights) 20C30: Representations of finite symmetric groups

Information

Type
Article
Information
Canadian Journal of Mathematics , First View , pp. 1 - 36
Check for updates
Copyright
© The Author(s), 2025. Published by Cambridge University Press on behalf of Canadian Mathematical Society

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

Footnotes

The first author is supported by the NSF of China (Grant No. 12401037) and NUDT (Grant No. 202401-YJRC-XX-002). The second author is supported by the NSF of China (Grants Nos. 12071026 and 12471025) and Anhui Provincial Natural Science Foundation (Grant No. 2308085MA01). The second author is also supported by the Fundamental Research Funds for the Central Universities JZ2025HGTG0251.

References

Borodin, Y. and Rozhkovskaya, N., On a super-analog of the Schur-Weyl duality. Preprint, (2022). arXiv:2208.07434.Google Scholar
Carter, R. W., Lie algebras of finite and affine type, Cambridge Studies in Advanced Mathematics, 96, Cambridge University Press, Cambridge, 2005, xviii+632 pp.Google Scholar
Cheng, S.-J. and Wang, W., Dualities and representations of Lie superalgebras, Graduate Student in Mathematics, 144, American Mathematical Society, Providence, RI, 2012, xviii+302 pp.Google Scholar
Coulembier, K., Tensor ideals, Deligne categories and invariant theory . Sel. Math. 24(2018), 4659–4710.Google Scholar
Coulembier, K., The periplectic Brauer algebra . Proc. Lond. Math. Soc. 117(2018), 441–482.Google Scholar
Deligne, P., Lehrer, G. I., and Zhang, R. B., The first fundamental theorem of invariant theory for the orthosymplectic super group . Adv. Math. 327(2018), 4–24.Google Scholar
Ehrig, M. and Stroppel, C., Schur-Weyl duality for the Brauer algebra and the ortho-symplectic Lie superalgebra . Math. Z. 284(2016), 595–613.Google Scholar
Gorelik, M., The center of a simple $P$ -type Lie superalgebra . J. Algebra 246(2001), 414–428.Google Scholar
Iorgov, N., Molev, A. I., and Ragoucy, E., Casimir elements from the Brauer-Schur-Weyl duality . J. Algebra 387(2013), 144–159.Google Scholar
Jarvis, P. D. and Green, H. S., Casimir invariants and characteristic identities for generators of the general linear, special linear and orthosymplectic graded Lie algebras . J. Math. Phys. 20(1979), 2115–2122.Google Scholar
Jarvis, P. D. and Murray, M. K., Casimir invariants, characteristic identities, and tensor operators for “strange” superalgebras . J. Math. Phys. 24(1983), 1705–1710.Google Scholar
Kac, V., Lie superalgebras . Adv. Math. 16(1977), 8–96.Google Scholar
Kerov, S. and Olshanski, G., Polynomial functions on the set of young diagrams . C. R. Acad. Sci. Paris Ser. I Math. 319(1994), 121–126.Google Scholar
Lehrer, G. I. and Zhang, R. B., The second fundamental theorem of invariant theory for the orthogonal group . Ann. Math. 176(2012), 2031–2054.Google Scholar
Lehrer, G. I. and Zhang, R. B., The Brauer category and invariant theory . J. Eur. Math. Soc. 17(2015), 2311–2351.Google Scholar
Lehrer, G. I. and Zhang, R. B., Invariants of the orthosymplectic Lie superalgebra and super Pfaffians . Math. Z. 286(2017), 893–917.Google Scholar
Lehrer, G. I. and Zhang, R. B., The first fundamental theorem of invariant theory for the orthosymplectic supergroup . Commun. Math. Phys. 349(2017), 661–702.Google Scholar
Lehrer, G. I. and Zhang, R. B., The second fundamental theorem of invariant theory for the orthosymplectic supergroup . Nagoya Math. J. 242(2021), 52–76.Google Scholar
Lehrer, G. I. and Zhang, R. B., Polar Brauer categories, infinitesimal braids and Lie superalgebra repesentations. Preprint, 2024. arXiv:2404.00515.Google Scholar
MacDonald, I. G., Symmetric functions and Hall polynomials. 2nd ed., Oxford University Press, Symmetric functions and Hall polynomials. Oxford Math. Monogr. Oxford Sci. Publ. The Clarendon Press, Oxford University Press, New York, 1995, x+475 pp.Google Scholar
Mazorchuk, V., Parabolic category for classical Lie superalgebras, Springer INdAM Series, 7, Springer, Cham, 2014, pp. 149–166.Google Scholar
Molev, A. I., Sugawara operators for classical Lie algebras, Mathematical Surveys and Monographs, 229 American Mathematical Society, Providence, RI, 2018, xiv+304 pp.Google Scholar
Molev, A. I. and Retakh, V., Quasideterminants and Casimir elements for the general linear Lie superalgebra . Int. Math. Res. Not. 13(2004), 611–619.Google Scholar
Moon, D., The product representations of the Lie siperalgebra ${\mathfrak{p}}_n$ and their centralizers . Commun. Algebra 31(2003), 2095–2140.Google Scholar
Musson, I. M., Lie superalgebras and enveloping algebras, Graduate Student in Mathematics, 131, American Mathematical Society, Providence, RI, 2012, xx+488 pp.Google Scholar
Nazarov, M. and Sergeev, A. N., Centralizer construction of the Yangian of the queer Lie superalgebra, Progress in Mathematics, 243, Birkhäuser Boston, Inc., Boston, MA, 2006, pp. 417–441.Google Scholar
Okounkov, A., Quantum immanants and higher Capelli identities . Transform. Groups 1(1996), 99–126.Google Scholar
Okounkov, A. and Olshanksi, G., Shifted Schur functions . St. Petersburg Math. J. 9(1998), 239–300.Google Scholar
Scheunert, M., Eigenvalues of Casimir operators for the general linear, the special linear, and the orthosymplectic Lie superalgebras . J. Math. Phys. 24(1983), 2681–2688.Google Scholar
Scheunert, M., Invariant supersymmetric multilinear forms and the Casimir elements of $P$ -type Lie superalgebras . J. Math. Phys. 28(1987), 1180–1191.Google Scholar
Sergeev, A. N., The center of enveloping algebra for Lie superalgebra $Q\left(n,\mathbb{C}\right)$ . Lett. Math. Phys. 7(1983), 177–179.Google Scholar
Sergeev, A. N., Tensor algebra of the identity representation as a module over the Lie superalgebras $GL\left(n,m\right)$ and $Q(n)$ . Math. Sb. (N. S.) 123(1984), 422–430.Google Scholar