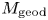1. Introduction
The deformation space of convex cocompact structures ![]() $CC(N)$ on a hyperbolizable
$CC(N)$ on a hyperbolizable ![]() $3$-manifold
$3$-manifold ![]() $N$ has a natural flow
$N$ has a natural flow ![]() $V$, first studied in [Reference Bridgeman, Brock and BrombergBBB19]. This flow
$V$, first studied in [Reference Bridgeman, Brock and BrombergBBB19]. This flow ![]() $V$ has a classical description; at a point
$V$ has a classical description; at a point ![]() $M \in CC(N)$ it is the Weil–Petersson dual of the Schwarzian derivative of the maps uniformizing the components of the conformal boundary
$M \in CC(N)$ it is the Weil–Petersson dual of the Schwarzian derivative of the maps uniformizing the components of the conformal boundary ![]() $\partial _cM$ of
$\partial _cM$ of ![]() $M$. Work of Storm proved that the convex core volume is minimized if and only if
$M$. Work of Storm proved that the convex core volume is minimized if and only if ![]() $N$ is acylindrical, with the minimum given by the manifold
$N$ is acylindrical, with the minimum given by the manifold ![]() $M_{\rm geod}$ whose convex core boundary is totally geodesic (see [Reference StormSto07]). A natural conjecture is that the flow
$M_{\rm geod}$ whose convex core boundary is totally geodesic (see [Reference StormSto07]). A natural conjecture is that the flow ![]() $V$ uniformizes
$V$ uniformizes ![]() $N$. Specifically, that for any flowline
$N$. Specifically, that for any flowline ![]() $M_t$ of
$M_t$ of ![]() $V$ we have
$V$ we have ![]() $M_t \rightarrow M_{\rm geod}$. In this paper, we prove this conjecture and extend it to the class of relatively acylindrical manifolds.
$M_t \rightarrow M_{\rm geod}$. In this paper, we prove this conjecture and extend it to the class of relatively acylindrical manifolds.
Although the flow has the above classical description in terms of the Schwarzian derivative, it only arose recently in the study of renormalized volume. This perspective will not be needed in this paper, but renormalized volume gives an analytic function ![]() ${{{\rm Vol}_R}}:CC(N)\rightarrow \mathbb {R}$ and the flow
${{{\rm Vol}_R}}:CC(N)\rightarrow \mathbb {R}$ and the flow ![]() $V$ is equal to the Weil–Petersson gradient flow of
$V$ is equal to the Weil–Petersson gradient flow of ![]() $-{{{\rm Vol}_R}}$. Renormalized volume was introduced in work of Graham and Witten [Reference Graham and WittenGW99] in physics to give an alternative notion of volume for conformally compact Einstein manifolds. In the hyperbolic setting, this was described and developed in the papers [Reference Takhtajan and TeoTT03, Reference Zograf and TakhtadzhyanZT87, Reference Krasnov and SchlenkerKS08, Reference Krasnov and SchlenkerKS12] of Takhtajan, Zograf, Teo, Krasnov, and Schlenker. The renormalized volume
$-{{{\rm Vol}_R}}$. Renormalized volume was introduced in work of Graham and Witten [Reference Graham and WittenGW99] in physics to give an alternative notion of volume for conformally compact Einstein manifolds. In the hyperbolic setting, this was described and developed in the papers [Reference Takhtajan and TeoTT03, Reference Zograf and TakhtadzhyanZT87, Reference Krasnov and SchlenkerKS08, Reference Krasnov and SchlenkerKS12] of Takhtajan, Zograf, Teo, Krasnov, and Schlenker. The renormalized volume ![]() ${{\rm Vol}_R}(M)$ of a hyperbolic manifold
${{\rm Vol}_R}(M)$ of a hyperbolic manifold ![]() $M$ connects many analytic concepts from the deformation theory with the geometry of
$M$ connects many analytic concepts from the deformation theory with the geometry of ![]() $M$ and is closely related to classical objects such as the convex core volume
$M$ and is closely related to classical objects such as the convex core volume ![]() ${{\rm Vol}_C}(M)$ and the Weil–Petersson geometry of Teichmüller space. For the description of these connections, we refer the reader to the earlier papers [Reference Bridgeman, Brock and BrombergBBB19, Reference Bridgeman, Brock and BrombergBBB22] for this perspective.
${{\rm Vol}_C}(M)$ and the Weil–Petersson geometry of Teichmüller space. For the description of these connections, we refer the reader to the earlier papers [Reference Bridgeman, Brock and BrombergBBB19, Reference Bridgeman, Brock and BrombergBBB22] for this perspective.
1.1 Flow on a deformation space of relatively acylindrical manifold
For ![]() $N$ a compact hyperbolizable
$N$ a compact hyperbolizable ![]() $3$-manifold, we denote by
$3$-manifold, we denote by ![]() $CC(N)$ the space of convex cocompact hyperbolic structures on the interior of
$CC(N)$ the space of convex cocompact hyperbolic structures on the interior of ![]() $N$. We consider triples
$N$. We consider triples ![]() $(N;S,X)$ where
$(N;S,X)$ where ![]() $S$ is a union of components of
$S$ is a union of components of ![]() $\partial N$ and
$\partial N$ and ![]() $X$ a conformal structure on
$X$ a conformal structure on ![]() $\partial N-S$. We then define
$\partial N-S$. We then define ![]() $CC(N;S,X) \subseteq CC(N)$ to be the subset with conformal structure
$CC(N;S,X) \subseteq CC(N)$ to be the subset with conformal structure ![]() $X$ on
$X$ on ![]() $\partial N-S$. The pair
$\partial N-S$. The pair ![]() $(N;S)$ is relatively acylindrical if there are no non-trivial annuli with boundary curves both in
$(N;S)$ is relatively acylindrical if there are no non-trivial annuli with boundary curves both in ![]() $S$. There are two important examples. The first is when
$S$. There are two important examples. The first is when ![]() $S = \partial N$ and
$S = \partial N$ and ![]() $N$ is a acylindrical. The second important example is the pair
$N$ is a acylindrical. The second important example is the pair ![]() $(S\times [0,1],S\times \{0\})$ where
$(S\times [0,1],S\times \{0\})$ where ![]() $S$ is a closed surface. Then
$S$ is a closed surface. Then ![]() $CC(S\times [0,1];S\times \{0\},X)$ is called the Bers slice and denoted by
$CC(S\times [0,1];S\times \{0\},X)$ is called the Bers slice and denoted by ![]() $\mathcal {B}_X$. While these may be the two main cases of interest, our result will hold in the general setting of
$\mathcal {B}_X$. While these may be the two main cases of interest, our result will hold in the general setting of ![]() $CC(N;S,X)$ for any relatively acylindrical
$CC(N;S,X)$ for any relatively acylindrical ![]() $(N;S)$. By the classical deformation theory of Kleinian groups (see [Reference KraKra74]),
$(N;S)$. By the classical deformation theory of Kleinian groups (see [Reference KraKra74]), ![]() $CC(N;S,X)$ is parameterized by the Teichmüller space
$CC(N;S,X)$ is parameterized by the Teichmüller space ![]() $\operatorname {Teich}(S)$ of conformal or hyperbolic structures on
$\operatorname {Teich}(S)$ of conformal or hyperbolic structures on ![]() $S$. Combined with Thurston's hyperbolization theorem, this deformation theory also implies that there is a unique
$S$. Combined with Thurston's hyperbolization theorem, this deformation theory also implies that there is a unique ![]() $M_{\rm geod} \in CC(N;S,X)$ such that
$M_{\rm geod} \in CC(N;S,X)$ such that ![]() $\partial _c M_{\rm geod} = X \sqcup Y_{\rm geod}$ and the convex core of
$\partial _c M_{\rm geod} = X \sqcup Y_{\rm geod}$ and the convex core of ![]() $M_{\rm geod}$ has totally geodesic boundary facing
$M_{\rm geod}$ has totally geodesic boundary facing ![]() $Y_{\rm geod}$.
$Y_{\rm geod}$.
Given ![]() $Y\in \operatorname {Teich}(S)$, we let
$Y\in \operatorname {Teich}(S)$, we let ![]() $M _Y\in CC(N;S,X)$ be the convex cocompact hyperbolic
$M _Y\in CC(N;S,X)$ be the convex cocompact hyperbolic ![]() $3$-manifold whose conformal boundary restricted to
$3$-manifold whose conformal boundary restricted to ![]() $S$ is
$S$ is ![]() $Y$. Let
$Y$. Let ![]() $\Gamma _Y$ be a Kleinian group with
$\Gamma _Y$ be a Kleinian group with ![]() $M_Y = {{\mathbb {H}}^3}/\Gamma _Y$ and let
$M_Y = {{\mathbb {H}}^3}/\Gamma _Y$ and let ![]() $\Omega _Y$ be the union of components of the domain of discontinuity of
$\Omega _Y$ be the union of components of the domain of discontinuity of ![]() $\Gamma _Y$ that project to
$\Gamma _Y$ that project to ![]() $Y$. The components of
$Y$. The components of ![]() $\Omega _Y$ will be Jordan domains in
$\Omega _Y$ will be Jordan domains in ![]() $\widehat {{\mathbb {C}}}$. Given a component
$\widehat {{\mathbb {C}}}$. Given a component ![]() $\Omega$ of
$\Omega$ of ![]() $\Omega _Y$, let
$\Omega _Y$, let ![]() $f\colon {\mathbb {H}}^2\to \Omega$ be a uniformizing univalent map. The Schwarzian derivative
$f\colon {\mathbb {H}}^2\to \Omega$ be a uniformizing univalent map. The Schwarzian derivative ![]() $S(f)$ defines a holomorphic quadratic differential on
$S(f)$ defines a holomorphic quadratic differential on ![]() $\Omega$. If we repeat this construction for every component of
$\Omega$. If we repeat this construction for every component of ![]() $\Omega _Y$ we get a
$\Omega _Y$ we get a ![]() $\Gamma _Y$-invariant holomorphic quadratic on
$\Gamma _Y$-invariant holomorphic quadratic on ![]() $\Omega$ which will descend to a holomorphic quadratic differential
$\Omega$ which will descend to a holomorphic quadratic differential ![]() $\phi _Y$ on
$\phi _Y$ on ![]() $Y$.
$Y$.
Recalling that we have an isomorphism ![]() $CC(N;S,X) \cong \operatorname {Teich}(S)$ and that tangent vectors in
$CC(N;S,X) \cong \operatorname {Teich}(S)$ and that tangent vectors in ![]() $T_Y\operatorname {Teich}(S)$ are given by Beltrami differentials on
$T_Y\operatorname {Teich}(S)$ are given by Beltrami differentials on ![]() $Y$, we can define a vector field
$Y$, we can define a vector field ![]() $V= V_{(N;S,X)}$ on
$V= V_{(N;S,X)}$ on ![]() $\operatorname {Teich}(S)$ by taking the harmonic Beltrami differential associated to
$\operatorname {Teich}(S)$ by taking the harmonic Beltrami differential associated to ![]() $\phi _Y$. Namely, let
$\phi _Y$. Namely, let
where ![]() $\rho _Y$ is the area form for the hyperbolic metric on
$\rho _Y$ is the area form for the hyperbolic metric on ![]() $Y$. The expression inside the brackets is a Beltrami differential, with the brackets indicating that we are taking the equivalence class in the tangent space
$Y$. The expression inside the brackets is a Beltrami differential, with the brackets indicating that we are taking the equivalence class in the tangent space ![]() $T_Y\operatorname {Teich}(S)$. Thus,
$T_Y\operatorname {Teich}(S)$. Thus, ![]() $V$ is a vector field on
$V$ is a vector field on ![]() $\operatorname {Teich}(S)$. Of course, the identification
$\operatorname {Teich}(S)$. Of course, the identification ![]() $CC(N;S,X) \cong \operatorname {Teich}(S))$ also allows us to consider
$CC(N;S,X) \cong \operatorname {Teich}(S))$ also allows us to consider ![]() $V$ as a vector field on
$V$ as a vector field on ![]() $CC(N;S,X)$. Conceptually this may be preferable as the hyperbolic structures determine
$CC(N;S,X)$. Conceptually this may be preferable as the hyperbolic structures determine ![]() $V$. However, much of the actual work (after the definition) will only involve Teichmüller space and we will move freely between the two viewpoints. As we will discuss below,
$V$. However, much of the actual work (after the definition) will only involve Teichmüller space and we will move freely between the two viewpoints. As we will discuss below, ![]() $V$ is the Weil–Petersson gradient of the negative of the renormalized volume function on
$V$ is the Weil–Petersson gradient of the negative of the renormalized volume function on ![]() $CC(N;S,X) \cong \operatorname {Teich}(S)$.
$CC(N;S,X) \cong \operatorname {Teich}(S)$.
Our main result is the following theorem.
Theorem 1.1 Let ![]() $(N;S)$ be relatively acylindrical and
$(N;S)$ be relatively acylindrical and ![]() $M_t \in \operatorname {Teich}(S)$ be a flowline for
$M_t \in \operatorname {Teich}(S)$ be a flowline for ![]() $V = V_{(N;S,X)}$. Then
$V = V_{(N;S,X)}$. Then ![]() $M_t$ converges to
$M_t$ converges to ![]() $M_{\rm geod}$.
$M_{\rm geod}$.
For the case of ![]() $N$ being acylindrical, the above states that the flow
$N$ being acylindrical, the above states that the flow ![]() $V$ uniformizes
$V$ uniformizes ![]() $N$ in that every convex cocompact structure flows to the unique structure
$N$ in that every convex cocompact structure flows to the unique structure ![]() $M_{\rm geod}$ with totally geodesic boundary. This is also the structure with minimal convex core volume (see [Reference StormSto07]).
$M_{\rm geod}$ with totally geodesic boundary. This is also the structure with minimal convex core volume (see [Reference StormSto07]).
We note that the existence of the manifold ![]() $M_{\rm geod}$ is a consequence of Thurston's hyperbolization theorem along with the deformation theory of Kleinian groups mentioned above, and in fact the manifold
$M_{\rm geod}$ is a consequence of Thurston's hyperbolization theorem along with the deformation theory of Kleinian groups mentioned above, and in fact the manifold ![]() $M_{\rm geod}$ only exists if
$M_{\rm geod}$ only exists if ![]() $(N;S)$ is relatively acylindrical. More precisely, the proof is (a special case of) the induction step in the proof of Thurston's theorem which is to find a fixed point of the skinning map on Teichmüller space. Thurston proved this by showing that the skinning map has bounded image (see [Reference ThurstonThu86]). McMullen gave an alternative proof by showing that this skinning map was a strict contraction (see [Reference McMullenMcM90]). Our proof uses McMullen's contraction of the skinning map at two key moments, although for one, Thurston's bounded image theorem would also work. So we are not giving a new proof of this existence theorem. It would be very interesting to give a more direct proof of Theorem 1.1 that did not depend on these two results, which would give an alternative proof of the existence of
$(N;S)$ is relatively acylindrical. More precisely, the proof is (a special case of) the induction step in the proof of Thurston's theorem which is to find a fixed point of the skinning map on Teichmüller space. Thurston proved this by showing that the skinning map has bounded image (see [Reference ThurstonThu86]). McMullen gave an alternative proof by showing that this skinning map was a strict contraction (see [Reference McMullenMcM90]). Our proof uses McMullen's contraction of the skinning map at two key moments, although for one, Thurston's bounded image theorem would also work. So we are not giving a new proof of this existence theorem. It would be very interesting to give a more direct proof of Theorem 1.1 that did not depend on these two results, which would give an alternative proof of the existence of ![]() $M_{\rm geod}$.
$M_{\rm geod}$.
The deformation space ![]() $CC(N; S,X)$ is homeomorphic to an open ball and the vector field
$CC(N; S,X)$ is homeomorphic to an open ball and the vector field ![]() $V$ has a single, attracting zero (see [Reference MoroianuMor17, Reference Vargas PalleteVar19]) so it may not seem surprising that the flow converges to this zero. However, the boundary of
$V$ has a single, attracting zero (see [Reference MoroianuMor17, Reference Vargas PalleteVar19]) so it may not seem surprising that the flow converges to this zero. However, the boundary of ![]() $CC(N; S, X)$ appears to exhibit fractal behavior which the vector field must wind its way through to find the zero. For example, if
$CC(N; S, X)$ appears to exhibit fractal behavior which the vector field must wind its way through to find the zero. For example, if ![]() $CC(N; S, X)$ is the Bers slice
$CC(N; S, X)$ is the Bers slice ![]() $\mathcal {B}_X$ then the Bers embedding identifies
$\mathcal {B}_X$ then the Bers embedding identifies ![]() $\mathcal {B}_X$ with a bounded open topological ball in the finite-dimensional vector space
$\mathcal {B}_X$ with a bounded open topological ball in the finite-dimensional vector space ![]() $Q(X)$ of holomorphic quadratic differentials on
$Q(X)$ of holomorphic quadratic differentials on ![]() $X$. When
$X$. When ![]() $\mathcal {B}_X$ has complex dimension
$\mathcal {B}_X$ has complex dimension ![]() $1$, Komori, Sugawa, Wada, and Yamashita (see [Reference Komori, Sugawa, Wada and YamashitaKSWY06]) and Dumas (see [Reference DumasDum1] for images and [Reference DumasDum2] for software) have drawn pictures that reveal this fractal behavior. More rigorously, also for dimension
$1$, Komori, Sugawa, Wada, and Yamashita (see [Reference Komori, Sugawa, Wada and YamashitaKSWY06]) and Dumas (see [Reference DumasDum1] for images and [Reference DumasDum2] for software) have drawn pictures that reveal this fractal behavior. More rigorously, also for dimension ![]() $1$, Miyachi (see [Reference MiyachiMiy03]) has shown that ‘cusped’ manifolds on the boundary of
$1$, Miyachi (see [Reference MiyachiMiy03]) has shown that ‘cusped’ manifolds on the boundary of ![]() $\mathcal {B}_X$ correspond to cusps in the boundary of
$\mathcal {B}_X$ correspond to cusps in the boundary of ![]() $\mathcal {B}_X$ itself. By McMullen [Reference McMullenMcM91] cusped manifolds are dense in the boundary of
$\mathcal {B}_X$ itself. By McMullen [Reference McMullenMcM91] cusped manifolds are dense in the boundary of ![]() $\mathcal {B}_X$, so together this implies that the boundary of
$\mathcal {B}_X$, so together this implies that the boundary of ![]() $\mathcal {B}_X$ has a dense set of cusps, a more concrete indication of the fractal nature of
$\mathcal {B}_X$ has a dense set of cusps, a more concrete indication of the fractal nature of ![]() $\mathcal {B}_X$. The flow
$\mathcal {B}_X$. The flow ![]() $V$ is a natural flow that gives a contraction of these complicated domains to the Fuchsian basepoint.
$V$ is a natural flow that gives a contraction of these complicated domains to the Fuchsian basepoint.
The proof in the Bers slice case and the general case differ only in that the general case requires additional analysis to show that the extra components (called leopard spots) in the domain of discontinuity do not contribute to the limiting model flow detailed below. For clarity of exposition, we have isolated this additional analysis to § 5.
We conclude this introduction with a informal discussion of the flow ![]() $V$ when
$V$ when ![]() $N$ is acylindrical (so
$N$ is acylindrical (so ![]() $S = \partial N$). A construction of C. Epstein (see [Reference EpsteinEps84]) describes a surface
$S = \partial N$). A construction of C. Epstein (see [Reference EpsteinEps84]) describes a surface ![]() $Y'$ in
$Y'$ in ![]() $M_Y$ associated to the hyperbolic metric on
$M_Y$ associated to the hyperbolic metric on ![]() $Y$. This surface cuts off a compact core of
$Y$. This surface cuts off a compact core of ![]() $M_Y$ which is closely related to the convex core. When the
$M_Y$ which is closely related to the convex core. When the ![]() $L^2$-norm of the Schwarzian is small the curvature is small. In particular, the integral of the mean curvature will be small. The difficulty is that this does not imply that the curvature is small everywhere in
$L^2$-norm of the Schwarzian is small the curvature is small. In particular, the integral of the mean curvature will be small. The difficulty is that this does not imply that the curvature is small everywhere in ![]() $Y'$ but only on the
$Y'$ but only on the ![]() $\epsilon$-thick part of
$\epsilon$-thick part of ![]() $Y'$ for some small
$Y'$ for some small ![]() $\epsilon$. When we start flowing along
$\epsilon$. When we start flowing along ![]() $V$ in
$V$ in ![]() $CC(N)$ the flow will try to locally deform
$CC(N)$ the flow will try to locally deform ![]() $Y'$ to decrease its curvature. This puts the thick and thin parts in competition – to decrease the curvature in the thick part we need to increase it in the thin part and vice versa. Our central conclusion is that the thin part eventually wins – the flow will eventually decrease curvature in the thin part even at the cost of increasing it in the thick part. As this happens, the short curves will become longer as the flow travels to a different point in Teichmüller space. This process can repeat but in [Reference Bridgeman, Brock and BrombergBBB22] we saw that it can only happen a finite number of times, and eventually the Epstein surface will converge to a totally geodesic surface that bounds the convex core of the limiting manifold which therefore must be
$Y'$ to decrease its curvature. This puts the thick and thin parts in competition – to decrease the curvature in the thick part we need to increase it in the thin part and vice versa. Our central conclusion is that the thin part eventually wins – the flow will eventually decrease curvature in the thin part even at the cost of increasing it in the thick part. As this happens, the short curves will become longer as the flow travels to a different point in Teichmüller space. This process can repeat but in [Reference Bridgeman, Brock and BrombergBBB22] we saw that it can only happen a finite number of times, and eventually the Epstein surface will converge to a totally geodesic surface that bounds the convex core of the limiting manifold which therefore must be ![]() $M_{\rm geod}$.
$M_{\rm geod}$.
1.2 The limiting model flow
In order to prove our main theorem, we show that if a flowline does not converge to ![]() $M_{\rm geod}$ then we can extract a limiting model flow as the flowline tends a point in the Weil–Petersson completion. We then use the properties of this model flow to obtain a contradiction. We now describe the limiting model flow.
$M_{\rm geod}$ then we can extract a limiting model flow as the flowline tends a point in the Weil–Petersson completion. We then use the properties of this model flow to obtain a contradiction. We now describe the limiting model flow.
Identifying the hyperbolic plane with the upper half-plane in ![]() $\mathbb {C}$, we consider the space of univalent maps
$\mathbb {C}$, we consider the space of univalent maps ![]() $f_c\colon {\mathbb {H}}^2 \rightarrow \hat{\mathbb {C}}$ of the form
$f_c\colon {\mathbb {H}}^2 \rightarrow \hat{\mathbb {C}}$ of the form ![]() $f_c(z) = z^c$ whose image is a Jordan domain. This is subspace of the space of all univalent maps on
$f_c(z) = z^c$ whose image is a Jordan domain. This is subspace of the space of all univalent maps on ![]() ${\mathbb {H}}^2$ and it corresponds to the open disk
${\mathbb {H}}^2$ and it corresponds to the open disk ![]() $\mathcal {D} = \{ f_c\ | \ |c-1| < 1\}$ (see Lemma 4.2). For each
$\mathcal {D} = \{ f_c\ | \ |c-1| < 1\}$ (see Lemma 4.2). For each ![]() $f_c \in \mathcal {D}$ define a Beltrami differential
$f_c \in \mathcal {D}$ define a Beltrami differential ![]() $\mu _c$ on
$\mu _c$ on ![]() $\widehat {{\mathbb {C}}}$ such
$\widehat {{\mathbb {C}}}$ such
and ![]() $\mu _c$ is zero on the complement of the image of
$\mu _c$ is zero on the complement of the image of ![]() $f_c$.
$f_c$.
This family of Beltrami differentials defines a flow on ![]() ${\mathcal {D}}$ as follows. For any
${\mathcal {D}}$ as follows. For any ![]() $f_c \in {\mathcal {D}}$ there is a family of quasiconformal homeomorphisms
$f_c \in {\mathcal {D}}$ there is a family of quasiconformal homeomorphisms ![]() $\psi _t \colon \widehat {{\mathbb {C}}} \to \widehat {{\mathbb {C}}}$ whose infinitesimal Beltrami differential at
$\psi _t \colon \widehat {{\mathbb {C}}} \to \widehat {{\mathbb {C}}}$ whose infinitesimal Beltrami differential at ![]() $t=0$ is
$t=0$ is ![]() $\mu _c$ and there is a smooth path
$\mu _c$ and there is a smooth path ![]() $f_{c_t}$ such that
$f_{c_t}$ such that ![]() $f_{c_t}({\mathbb {H}}^2) = \psi _t(f_c({\mathbb {H}}^2))$. Furthermore, the
$f_{c_t}({\mathbb {H}}^2) = \psi _t(f_c({\mathbb {H}}^2))$. Furthermore, the ![]() $\psi _t$ are defined for
$\psi _t$ are defined for ![]() $t\in \mathbb {R}$ and the flowline starting at
$t\in \mathbb {R}$ and the flowline starting at ![]() $f_{c_s} \in {\mathcal {D}}$ is given by the formula
$f_{c_s} \in {\mathcal {D}}$ is given by the formula ![]() $\psi _{t+s}\circ \psi _{-s}$.
$\psi _{t+s}\circ \psi _{-s}$.
The map ![]() $f_c\mapsto c$ is a homeomorphism from
$f_c\mapsto c$ is a homeomorphism from ![]() ${\mathcal {D}}$ to the disk
${\mathcal {D}}$ to the disk ![]() $|z-1| < 1$ in
$|z-1| < 1$ in ![]() $\mathbb {C}$ and the flow on
$\mathbb {C}$ and the flow on ![]() ${\mathcal {D}}$ induces the flow
${\mathcal {D}}$ induces the flow ![]() $c_t$ on the disk (see Figure 1). In fact, we have the following formula for the flow:
$c_t$ on the disk (see Figure 1). In fact, we have the following formula for the flow:
Although these last two paragraphs could be made rigorous as they are not necessary to prove our main result, we will not do so. This formula for ![]() $v$ will follow from our derivation of the limiting vector field in our proof. However, to informally see the connection between this flow and the gradient flow
$v$ will follow from our derivation of the limiting vector field in our proof. However, to informally see the connection between this flow and the gradient flow ![]() $V$ one should view the domains
$V$ one should view the domains ![]() $f_c({\mathbb {H}}^2) \subset \widehat {{\mathbb {C}}}$ as approximations for a component of the domain discontinuity of a Kleinian group where the imaginary axis is the axis of some short curve in the conformal boundary and the constant
$f_c({\mathbb {H}}^2) \subset \widehat {{\mathbb {C}}}$ as approximations for a component of the domain discontinuity of a Kleinian group where the imaginary axis is the axis of some short curve in the conformal boundary and the constant ![]() $c$ is the ratio of the complex length of the curve in the hyperbolic
$c$ is the ratio of the complex length of the curve in the hyperbolic ![]() $3$-manifold to its length on the boundary. There is an explicit formula for the derivative of this length ratio (see § 2.1) and in Theorem 4.10 we calculate the limit of this formula as both the length on the boundary and the norm of the Schwarzian approach zero. The limiting formula we find is exactly the formula for the vector field
$3$-manifold to its length on the boundary. There is an explicit formula for the derivative of this length ratio (see § 2.1) and in Theorem 4.10 we calculate the limit of this formula as both the length on the boundary and the norm of the Schwarzian approach zero. The limiting formula we find is exactly the formula for the vector field ![]() $v$ above.
$v$ above.

Figure 1. Vector field ![]() $v$ on
$v$ on ![]() $\mathcal {D}$.
$\mathcal {D}$.
We can also connect the discussion here to our discussion of the flow in the previous subsection. In our model the situation when ![]() $c$ is near
$c$ is near ![]() $2$ corresponds to an acylindrical manifold where the surface
$2$ corresponds to an acylindrical manifold where the surface ![]() $Y'$ has small curvature outside of the
$Y'$ has small curvature outside of the ![]() $\epsilon$-thin part. where the closer
$\epsilon$-thin part. where the closer ![]() $c$ is to two the smaller we can choose
$c$ is to two the smaller we can choose ![]() $\epsilon$. When
$\epsilon$. When ![]() $c$ is near
$c$ is near ![]() $1$ it corresponds to
$1$ it corresponds to ![]() $Y'$ having small curvature everywhere. While the flow
$Y'$ having small curvature everywhere. While the flow ![]() $v$ may initially appear to be converging to
$v$ may initially appear to be converging to ![]() $2$, it will eventually turn around and head towards
$2$, it will eventually turn around and head towards ![]() $1$ which corresponds
$1$ which corresponds ![]() $Y'$ being totally geodesic and the hyperbolic manifold
$Y'$ being totally geodesic and the hyperbolic manifold ![]() $M_{\rm geod}$.
$M_{\rm geod}$.
While our discussion here is only informal we will see that the properties of this limiting model flow play a crucial role in the proof of our main theorem.
2. Weil–Petersson geometry
Let ![]() $S$ be a closed surface of genus
$S$ be a closed surface of genus ![]() $g \geq 2$. Then the Teichmüller space
$g \geq 2$. Then the Teichmüller space ![]() $\operatorname {Teich}(S)$ is the space of marked conformal structures on
$\operatorname {Teich}(S)$ is the space of marked conformal structures on ![]() $S$. Given
$S$. Given ![]() $X \in \operatorname {Teich}(S)$, the cotangent space
$X \in \operatorname {Teich}(S)$, the cotangent space ![]() $T^*_X(\operatorname {Teich}(S))$ is
$T^*_X(\operatorname {Teich}(S))$ is ![]() $Q(X)$, the space of holomorphic quadratic differentials on
$Q(X)$, the space of holomorphic quadratic differentials on ![]() $X$. We let
$X$. We let ![]() $B(X)$ be the space of Beltrami differentials on
$B(X)$ be the space of Beltrami differentials on ![]() $X$. Then there is a pairing between
$X$. Then there is a pairing between ![]() $Q(X)$ and
$Q(X)$ and ![]() $B(X)$ given by
$B(X)$ given by
If we let ![]() $N(X) \subseteq B(X)$ be the annihilator of
$N(X) \subseteq B(X)$ be the annihilator of ![]() $Q(X)$ under this pairing, we obtain the identification
$Q(X)$ under this pairing, we obtain the identification ![]() $T_X(\operatorname {Teich}(S)) = B(X)/N(X)$.
$T_X(\operatorname {Teich}(S)) = B(X)/N(X)$.
Given ![]() $\phi \in Q(X)$ and
$\phi \in Q(X)$ and ![]() $z \in X$, we define the pointwise norm by
$z \in X$, we define the pointwise norm by
where ![]() $\rho _X$ is the hyperbolic metric on
$\rho _X$ is the hyperbolic metric on ![]() $X$. We define the
$X$. We define the ![]() $L^p$ norm of
$L^p$ norm of ![]() $\phi$, denoted by
$\phi$, denoted by ![]() $\|\phi \|_p$, to be the
$\|\phi \|_p$, to be the ![]() $L^p$ norm of the function
$L^p$ norm of the function ![]() $\|\phi (z)\|$ with respect to the hyperbolic area form on
$\|\phi (z)\|$ with respect to the hyperbolic area form on ![]() $X$. These
$X$. These ![]() $L^p$ norms define Finsler cometrics on the cotangent bundle of
$L^p$ norms define Finsler cometrics on the cotangent bundle of ![]() $\operatorname {Teich}(S)$ and dual Finsler metrics on the tangent bundle of
$\operatorname {Teich}(S)$ and dual Finsler metrics on the tangent bundle of ![]() $\operatorname {Teich}(S)$. When
$\operatorname {Teich}(S)$. When ![]() $p=2$ this norm comes from an inner product and therefore determines a Riemannian metric on
$p=2$ this norm comes from an inner product and therefore determines a Riemannian metric on ![]() $\operatorname {Teich}(S)$ called the Weil–Petersson metric. Classical results are that the Weil–Petersson metric is incomplete (see [Reference ChuChu76, Reference WolpertWol75]) and strictly negatively curved (see [Reference TrombaTro86, Reference WolpertWol86]).
$\operatorname {Teich}(S)$ called the Weil–Petersson metric. Classical results are that the Weil–Petersson metric is incomplete (see [Reference ChuChu76, Reference WolpertWol75]) and strictly negatively curved (see [Reference TrombaTro86, Reference WolpertWol86]).
In order to describe the Weil–Petersson completion ![]() $\overline {\operatorname {Teich}(S)}$, we first describe the augmented Teichmüller space. For further details on the augmented Teichmüller space see [Reference AbikoffAbi77, Reference AbikoffAbi80, Reference HarveyHar77].
$\overline {\operatorname {Teich}(S)}$, we first describe the augmented Teichmüller space. For further details on the augmented Teichmüller space see [Reference AbikoffAbi77, Reference AbikoffAbi80, Reference HarveyHar77].
For ![]() $S$ a compact surface we let
$S$ a compact surface we let ![]() ${\mathcal {C}}(S)$ be the complex of curves, the simplicial complex organizing the isotopy classes of simple closed curves on
${\mathcal {C}}(S)$ be the complex of curves, the simplicial complex organizing the isotopy classes of simple closed curves on ![]() $S$ that do not represent boundary components. To each isotopy class
$S$ that do not represent boundary components. To each isotopy class ![]() $\alpha$ we associate a vertex
$\alpha$ we associate a vertex ![]() $v_\alpha$, and each
$v_\alpha$, and each ![]() $k$-simplex
$k$-simplex ![]() $\sigma$ is the span of
$\sigma$ is the span of ![]() $k+1$ vertices whose associated isotopy classes can be realized disjointly on
$k+1$ vertices whose associated isotopy classes can be realized disjointly on ![]() $S$.
$S$.
A point in the augmented Teichmüller space is given by a choice of multicurve ![]() $\tau$, a (
$\tau$, a (![]() $0$-skeleton of a) simplex in
$0$-skeleton of a) simplex in ![]() ${\mathcal {C}}(S)$, and finite-area hyperbolic structures on the complementary subsurfaces
${\mathcal {C}}(S)$, and finite-area hyperbolic structures on the complementary subsurfaces ![]() $S \,{\setminus}\, \tau$. The elements of
$S \,{\setminus}\, \tau$. The elements of ![]() $\tau$ are the nodes and the point of the completion is a noded Riemann surface. The augmented Teichmüller space is stratified by the simplices of
$\tau$ are the nodes and the point of the completion is a noded Riemann surface. The augmented Teichmüller space is stratified by the simplices of ![]() ${\mathcal {C}}(S)$: the collection of noded Riemann surfaces with nodes determined by a given simplex
${\mathcal {C}}(S)$: the collection of noded Riemann surfaces with nodes determined by a given simplex ![]() $\sigma$ lies in a product of lower-dimensional Teichmüller spaces determined by varying the structures on
$\sigma$ lies in a product of lower-dimensional Teichmüller spaces determined by varying the structures on ![]() $S \,{\setminus}\, \tau$. This stratum,
$S \,{\setminus}\, \tau$. This stratum, ![]() ${\mathcal {S}}_\tau$, inherits a natural metric from the Weil–Petersson metric, which by Masur (see [Reference MasurMas76]) is isometric to the product of Weil–Petersson metrics on the Teichmüller spaces of the complementary subsurfaces.
${\mathcal {S}}_\tau$, inherits a natural metric from the Weil–Petersson metric, which by Masur (see [Reference MasurMas76]) is isometric to the product of Weil–Petersson metrics on the Teichmüller spaces of the complementary subsurfaces.
It follows by Masur also that the augmented Teichmüller space is the Weil–Petersson completion ![]() $\overline {\operatorname {Teich}(S)}$. The completion naturally descends under the action of the mapping class group to a finite-diameter metric on the Deligne–Mumford compactification of the moduli space of Riemann surfaces. The strata of the completion can be described as follows:
$\overline {\operatorname {Teich}(S)}$. The completion naturally descends under the action of the mapping class group to a finite-diameter metric on the Deligne–Mumford compactification of the moduli space of Riemann surfaces. The strata of the completion can be described as follows:
where ![]() $\ell _\alpha$ is the extended length function of
$\ell _\alpha$ is the extended length function of ![]() $\alpha$.
$\alpha$.
2.1 Length functions and Gardiner's formula
For an essential closed curve ![]() $\alpha$ on
$\alpha$ on ![]() $S$ there are two natural length functions on the deformation space
$S$ there are two natural length functions on the deformation space ![]() $CC(N;S,X) \cong \operatorname {Teich}(S)$. The first is just the usual length function
$CC(N;S,X) \cong \operatorname {Teich}(S)$. The first is just the usual length function ![]() $\ell _\alpha \colon \operatorname {Teich}(S) \to \mathbb {R}_+$ on Teichmüller space where
$\ell _\alpha \colon \operatorname {Teich}(S) \to \mathbb {R}_+$ on Teichmüller space where ![]() $\ell _\alpha (Y)$ is the length of the geodesic representative of
$\ell _\alpha (Y)$ is the length of the geodesic representative of ![]() $\alpha$ on the hyperbolic surface
$\alpha$ on the hyperbolic surface ![]() $Y$. We have used this function already.
$Y$. We have used this function already.
The Gardiner formula is a formula for the differential ![]() $d\ell _\alpha$. To state it we identify the universal cover of
$d\ell _\alpha$. To state it we identify the universal cover of ![]() $Y$ with the upper half-plane normalized so that the imaginary axis is an axis for
$Y$ with the upper half-plane normalized so that the imaginary axis is an axis for ![]() $\alpha$. Then
$\alpha$. Then ![]() $z\mapsto e^{\ell _\alpha (Y)}z$ is an element of the deck group for
$z\mapsto e^{\ell _\alpha (Y)}z$ is an element of the deck group for ![]() $Y$. We let
$Y$. We let ![]() $A_\alpha$ be the quotient annulus for the action of this element. The annulus
$A_\alpha$ be the quotient annulus for the action of this element. The annulus ![]() $A_\alpha$ also covers
$A_\alpha$ also covers ![]() $Y$, so if
$Y$, so if ![]() $\mu$ is a Beltrami differential on
$\mu$ is a Beltrami differential on ![]() $Y$ (representing a tangent vector in
$Y$ (representing a tangent vector in ![]() $T_Y\operatorname {Teich}(S)$) then
$T_Y\operatorname {Teich}(S)$) then ![]() $\mu$ lifts to a Beltrami differential
$\mu$ lifts to a Beltrami differential ![]() $\mu _A$ on
$\mu _A$ on ![]() $A_\alpha$. The holomorphic quadratic differential
$A_\alpha$. The holomorphic quadratic differential ![]() $dz^2/z^2$ on
$dz^2/z^2$ on ![]() ${\mathbb {H}}^2$ is invariant under the action of
${\mathbb {H}}^2$ is invariant under the action of ![]() $z\mapsto e^{\ell _\alpha (Y)}z$ so descends to a Beltrami differential on
$z\mapsto e^{\ell _\alpha (Y)}z$ so descends to a Beltrami differential on ![]() $A_\alpha$. We will continue to refer to this quadratic differential as
$A_\alpha$. We will continue to refer to this quadratic differential as ![]() $dz^2/z^2$ on
$dz^2/z^2$ on ![]() $A_\alpha$. If we let
$A_\alpha$. If we let ![]() $\langle, \rangle _{A_\alpha}$ be the pairing between Beltrami differentials and quadratic differentials on
$\langle, \rangle _{A_\alpha}$ be the pairing between Beltrami differentials and quadratic differentials on ![]() $A_\alpha$ we have the following result.
$A_\alpha$ we have the following result.
Theorem 2.1 (Gardiner [Reference GardinerGar75])
The derivative of ![]() $\ell _\alpha$ on
$\ell _\alpha$ on ![]() $\operatorname {Teich}(S)$ is given by the formula
$\operatorname {Teich}(S)$ is given by the formula
If we consider ![]() $\alpha$ as a closed curve in the hyperbolic
$\alpha$ as a closed curve in the hyperbolic ![]() $3$-manifold
$3$-manifold ![]() $M_Y$ then
$M_Y$ then ![]() $\alpha$ has a complex length. The real part is just the length of the geodesic representative of
$\alpha$ has a complex length. The real part is just the length of the geodesic representative of ![]() $\alpha$ in
$\alpha$ in ![]() $M_Y$ while the imaginary part measures the twisting along the geodesic. We need the imaginary part to be a well defined real number (rather than just a number mod
$M_Y$ while the imaginary part measures the twisting along the geodesic. We need the imaginary part to be a well defined real number (rather than just a number mod ![]() $2\pi$). For this reason the definition is somewhat involved.
$2\pi$). For this reason the definition is somewhat involved.
Let ![]() $\Gamma _Y$ be a Kleinian group uniformizing
$\Gamma _Y$ be a Kleinian group uniformizing ![]() $M_Y \in CC(N;S,X)$ and let
$M_Y \in CC(N;S,X)$ and let ![]() $\Omega _Y$ be the components of the domain of discontinuity of
$\Omega _Y$ be the components of the domain of discontinuity of ![]() $\Gamma _Y$ that cover
$\Gamma _Y$ that cover ![]() $Y$. The pre-image of
$Y$. The pre-image of ![]() $\alpha$ in
$\alpha$ in ![]() $\Omega _Y$ will be a collection of arcs. Fixing an orientation of
$\Omega _Y$ will be a collection of arcs. Fixing an orientation of ![]() $\alpha$ fixes an orientation of each of the arcs and we can assume that the pre-image contains an oriented arc
$\alpha$ fixes an orientation of each of the arcs and we can assume that the pre-image contains an oriented arc ![]() $\tilde \alpha$ with initial endpoint
$\tilde \alpha$ with initial endpoint ![]() $0$ and terminal endpoint
$0$ and terminal endpoint ![]() $\infty$. Let
$\infty$. Let ![]() $\Omega \subset \Omega _Y$ be the component of the domain of discontinuity that contains
$\Omega \subset \Omega _Y$ be the component of the domain of discontinuity that contains ![]() $\tilde \alpha$ and let
$\tilde \alpha$ and let ![]() $\log$ be a branch of the logarithm defined on
$\log$ be a branch of the logarithm defined on ![]() $\Omega$. We then define
$\Omega$. We then define
by
where we are assuming the that ![]() $\tilde \alpha$ is parameterized by arc length. The complex length
$\tilde \alpha$ is parameterized by arc length. The complex length ![]() ${\mathcal {L}}_\alpha (M_Y)$ is independent of the choices we made in its definition.
${\mathcal {L}}_\alpha (M_Y)$ is independent of the choices we made in its definition.
The complex length is a holomorphic function on ![]() $CC(N:S,X)$ and we would also like a formula for its derivative. Miyachi observed [Reference MiyachiMiy03, First proposition, § 8] that the proof of Theorem 2.1 can also be applied to find the derivative of the complex length. As
$CC(N:S,X)$ and we would also like a formula for its derivative. Miyachi observed [Reference MiyachiMiy03, First proposition, § 8] that the proof of Theorem 2.1 can also be applied to find the derivative of the complex length. As ![]() $CC(N;X,S) \cong \operatorname {Teich}(S)$ if
$CC(N;X,S) \cong \operatorname {Teich}(S)$ if ![]() $\mu$ is a tangent vector in
$\mu$ is a tangent vector in ![]() $T_Y\operatorname {Teich}(S)$, we can also consider it as a tangent vector to
$T_Y\operatorname {Teich}(S)$, we can also consider it as a tangent vector to ![]() $CC(N;X,S)$ at
$CC(N;X,S)$ at ![]() $M_Y$. Then
$M_Y$. Then ![]() $\mu$ will lift to a
$\mu$ will lift to a ![]() $\Gamma _Y$-invariant Beltrami differential
$\Gamma _Y$-invariant Beltrami differential ![]() $\tilde \mu$ on
$\tilde \mu$ on ![]() $\Omega _Y$. We can extend
$\Omega _Y$. We can extend ![]() $\tilde \mu$ to be zero everywhere else. The Kleinian group
$\tilde \mu$ to be zero everywhere else. The Kleinian group ![]() $\Gamma _Y$ will contain the element
$\Gamma _Y$ will contain the element ![]() $z\mapsto e^{{\mathcal {L}}_\alpha (M_Y)}z$. The quotient of the
$z\mapsto e^{{\mathcal {L}}_\alpha (M_Y)}z$. The quotient of the ![]() $\mathbb {C}\smallsetminus \{0\}$ under the action of this element will be a torus
$\mathbb {C}\smallsetminus \{0\}$ under the action of this element will be a torus ![]() $T_\alpha$ and the Beltrami differential
$T_\alpha$ and the Beltrami differential ![]() $\tilde \mu$ will descend to a Beltrami differential
$\tilde \mu$ will descend to a Beltrami differential ![]() $\mu _T$ on
$\mu _T$ on ![]() $T_\alpha$. The quadratic differential
$T_\alpha$. The quadratic differential ![]() $dz^2/z^2$ will also descend to a quadratic differential on
$dz^2/z^2$ will also descend to a quadratic differential on ![]() $T_\alpha$. If
$T_\alpha$. If ![]() $\langle, \rangle _{T_\alpha }$ is the pairing on
$\langle, \rangle _{T_\alpha }$ is the pairing on ![]() $T_\alpha$ we have the following theorem.
$T_\alpha$ we have the following theorem.
Theorem 2.2 (Miyachi [Reference MiyachiMiy03])
The differential of ![]() ${\mathcal {L}}_\alpha$ is given by the formula
${\mathcal {L}}_\alpha$ is given by the formula
For what we will do below it will be useful to decompose this second Gardiner formula into two distinct terms. To describe this decomposition we note that the image of ![]() $\Omega$ in
$\Omega$ in ![]() $T_\alpha$ will be an essential annulus, while every other component of
$T_\alpha$ will be an essential annulus, while every other component of ![]() $\Omega _Y$ will map homeomorphically into
$\Omega _Y$ will map homeomorphically into ![]() $T_\alpha$ (see Figure 2). We then write
$T_\alpha$ (see Figure 2). We then write
where ![]() $\mu _T^{\rm cen}$ has support on the image of
$\mu _T^{\rm cen}$ has support on the image of ![]() $\Omega$ and the support of
$\Omega$ and the support of ![]() $\mu _T^{\rm aux}$ is in the image of the other components of
$\mu _T^{\rm aux}$ is in the image of the other components of ![]() $\Omega _Y$. Then
$\Omega _Y$. Then
are the central and auxiliary terms of the differential ![]() $d{\mathcal {L}}_\alpha (\mu )$.
$d{\mathcal {L}}_\alpha (\mu )$.

Figure 2. Leopard spots on Riemann sphere and quotient torus.
It will also be useful to write the central term as a pairing on the annulus ![]() $A_\alpha$. For this let
$A_\alpha$. For this let
be the uniformizing map, normalized so that ![]() $g$ takes the imaginary axis to
$g$ takes the imaginary axis to ![]() $\tilde \alpha$. Then the pullbacks
$\tilde \alpha$. Then the pullbacks ![]() $g^*\tilde \mu$ and
$g^*\tilde \mu$ and ![]() $g^*(dz^2/z^2)$ are both invariant under the isometry
$g^*(dz^2/z^2)$ are both invariant under the isometry ![]() $z\mapsto e^{\ell _\alpha (Y)}z$ and descend to objects on
$z\mapsto e^{\ell _\alpha (Y)}z$ and descend to objects on ![]() $A_\alpha$. In fact, the Beltrami differential will be the Beltrami differential
$A_\alpha$. In fact, the Beltrami differential will be the Beltrami differential ![]() $\mu _A$ that we defined above. We can then write the central term as
$\mu _A$ that we defined above. We can then write the central term as
Note that both the central and auxiliary terms only depend on the Beltrami differential ![]() $\mu$. For later convenience we let
$\mu$. For later convenience we let ![]() $J_\alpha (\mu )$ be the auxiliary term. Note that, for a Bers slice,
$J_\alpha (\mu )$ be the auxiliary term. Note that, for a Bers slice, ![]() $\Omega$ is the only component of
$\Omega$ is the only component of ![]() $\Omega _Y$ so the auxiliary term is always zero. The extra work in the relatively acylindrical case is estimating
$\Omega _Y$ so the auxiliary term is always zero. The extra work in the relatively acylindrical case is estimating ![]() $J_\alpha (\mu )$ when
$J_\alpha (\mu )$ when ![]() $\mu$ is a harmonic Beltrami differential with small
$\mu$ is a harmonic Beltrami differential with small ![]() $L^2$-norm.
$L^2$-norm.
3. Limits of the flow
As mentioned in the introduction, the flow ![]() $V$ is the negative of the Weil–Petersson gradient of the renormalized volume function
$V$ is the negative of the Weil–Petersson gradient of the renormalized volume function ![]() ${{{\rm Vol}_R}}$ on
${{{\rm Vol}_R}}$ on ![]() $CC(N;S,X)$. The definition of ‘renormalized’ is somewhat involved and not necessary for our work here. Therefore, we will omit it and restrict ourselves to discussing some of its important properties. The first of these is a variational formula.
$CC(N;S,X)$. The definition of ‘renormalized’ is somewhat involved and not necessary for our work here. Therefore, we will omit it and restrict ourselves to discussing some of its important properties. The first of these is a variational formula.
Theorem 3.1 [Reference Zograf and TakhtadzhyanZT87, Reference Takhtajan and TeoTT03, Reference Krasnov and SchlenkerKS12]
For tangent vector ![]() $\mu \in T_{M_Y} CC(N) \cong T_Y\operatorname {Teich}(S)$ we have
$\mu \in T_{M_Y} CC(N) \cong T_Y\operatorname {Teich}(S)$ we have
This formula implies that our flow ![]() $V$ is the Weil–Petersson gradient of
$V$ is the Weil–Petersson gradient of ![]() $-{{{\rm Vol}_R}}$.
$-{{{\rm Vol}_R}}$.
By the Nehari bound on the norm of the Schwarzian derivative of a univalent map (see [Reference NehariNeh49]), ![]() $V$ is bounded with respect to the Teichmüller metric on
$V$ is bounded with respect to the Teichmüller metric on ![]() $\operatorname {Teich}(S)$. Therefore, as the Teichmüller metric is complete, the flowlines exists for all time (see [Reference Bridgeman, Brock and BrombergBBB19] for further details).
$\operatorname {Teich}(S)$. Therefore, as the Teichmüller metric is complete, the flowlines exists for all time (see [Reference Bridgeman, Brock and BrombergBBB19] for further details).
Also by the gradient description of ![]() $V$ it follows that along a flowline
$V$ it follows that along a flowline ![]() $M_t$,
$M_t$,
As ![]() ${{{\rm Vol}_R}} \geq 0$ (see [Reference Bridgeman, Brock and BrombergBBB19]), it follows that
${{{\rm Vol}_R}} \geq 0$ (see [Reference Bridgeman, Brock and BrombergBBB19]), it follows that
We now describe the further properties of the flow proved in [Reference Bridgeman, Brock and BrombergBBB22] that we will need in our analysis.
Theorem 3.2 (Bridgeman–Brock–Bromberg [Reference Bridgeman, Brock and BrombergBBB22])
Let ![]() $(N,S)$ be relatively acylindrical and
$(N,S)$ be relatively acylindrical and ![]() $M_t = (X,Y_t)$ be a flowline for
$M_t = (X,Y_t)$ be a flowline for ![]() $V$ on
$V$ on ![]() $CC(N;S,X)$. Then the following assertions hold.
$CC(N;S,X)$. Then the following assertions hold.
(i)
 $Y_t \rightarrow \hat Y \in \overline {\operatorname {Teich}(S)}$ in the Weil–Petersson completion. Thus,
$Y_t \rightarrow \hat Y \in \overline {\operatorname {Teich}(S)}$ in the Weil–Petersson completion. Thus,  $\hat Y$ is a noded Riemann surface.
$\hat Y$ is a noded Riemann surface.(ii)
 $\|\phi _{Y_t}\|_2 \rightarrow 0$ as
$\|\phi _{Y_t}\|_2 \rightarrow 0$ as  $t\rightarrow \infty$.
$t\rightarrow \infty$.
In order to prove our main theorem, we need to prove that the set of nodes of any limit ![]() $\hat Y$ is empty or alternately that
$\hat Y$ is empty or alternately that ![]() $\hat Y \in \operatorname {Teich}(S)$. We will do this by assuming
$\hat Y \in \operatorname {Teich}(S)$. We will do this by assuming ![]() $\hat Y$ is noded and consider the limits of the projective structure as we zoom in on the nodes. This will produce our limiting model flow which will allow us to obtain a contradiction.
$\hat Y$ is noded and consider the limits of the projective structure as we zoom in on the nodes. This will produce our limiting model flow which will allow us to obtain a contradiction.
4. Taking limits at a node
The length functions ![]() $\ell _\alpha$ and
$\ell _\alpha$ and ![]() ${\mathcal {L}}_\alpha$ are smooth functions on
${\mathcal {L}}_\alpha$ are smooth functions on ![]() $CC(N;S,X) \cong \operatorname {Teich}(S)$. If we pair their differentials against the vector field
$CC(N;S,X) \cong \operatorname {Teich}(S)$. If we pair their differentials against the vector field ![]() $V$ we get a function on
$V$ we get a function on ![]() $\operatorname {Teich}(S)$. We would like to take the limit of these functions along the sequence
$\operatorname {Teich}(S)$. We would like to take the limit of these functions along the sequence ![]() $Y_n$ in
$Y_n$ in ![]() $\operatorname {Teich}(S)$ where
$\operatorname {Teich}(S)$ where ![]() $\|V(Y_n)\|_2 \to 0$. To do this we will map
$\|V(Y_n)\|_2 \to 0$. To do this we will map ![]() $CC(N;S,X)$ to a space of univalent functions. We then use normal families theorems for holomorphic functions to evaluate the limit. We begin by setting up our space.
$CC(N;S,X)$ to a space of univalent functions. We then use normal families theorems for holomorphic functions to evaluate the limit. We begin by setting up our space.
Let
be the space of quadratic differentials that arise as Schwarzian derivatives of univalent functions from ![]() ${\mathbb {H}}^2$ (realized as the upper half-plane) to
${\mathbb {H}}^2$ (realized as the upper half-plane) to ![]() $\mathbb {C}$. We give
$\mathbb {C}$. We give ![]() ${\mathcal {U}}$ the compact-open topology and recall some basic facts:
${\mathcal {U}}$ the compact-open topology and recall some basic facts:
–
 ${\mathcal {U}}$ is compact.
${\mathcal {U}}$ is compact.– If
 $\phi _n\to \phi$ and
$\phi _n\to \phi$ and  $f_n\to f$ (in the compact-open topology) with
$f_n\to f$ (in the compact-open topology) with  $S(f_n) = \phi _n$ then either
$S(f_n) = \phi _n$ then either  $f$ is constant or
$f$ is constant or  $f$ is univalent and
$f$ is univalent and  $S(f) = \phi$.
$S(f) = \phi$.
The following result is essentially Montel's theorem.
Theorem 4.1 Let ![]() $z_0$,
$z_0$, ![]() $z_1$ and
$z_1$ and ![]() $z_2$ be distinct points in
$z_2$ be distinct points in ![]() $\overline {\mathbb {H}}^2$ and
$\overline {\mathbb {H}}^2$ and ![]() $w_0$,
$w_0$, ![]() $w_1$ and
$w_1$ and ![]() $w_2$ distinct points in
$w_2$ distinct points in ![]() $\widehat {{\mathbb {C}}}$. Let
$\widehat {{\mathbb {C}}}$. Let ![]() ${\mathcal {F}}$ be a family of holomorphic maps on
${\mathcal {F}}$ be a family of holomorphic maps on ![]() ${\mathbb {H}}^2$ that extend continuously to the
${\mathbb {H}}^2$ that extend continuously to the ![]() $z_i$ if they are on the boundary of
$z_i$ if they are on the boundary of ![]() ${\mathbb {H}}^2$, and assume that for all
${\mathbb {H}}^2$, and assume that for all ![]() $f\in {\mathcal {F}}$ we have
$f\in {\mathcal {F}}$ we have ![]() $f(z_i) = w_i$ for
$f(z_i) = w_i$ for ![]() $i=0,1,2$ while if
$i=0,1,2$ while if ![]() $z$ is not in
$z$ is not in ![]() $\{z_0, z_1, z_2\}$ then
$\{z_0, z_1, z_2\}$ then ![]() $f(z)$ is not in
$f(z)$ is not in ![]() $\{w_0, w_1,w_2\}$. Then
$\{w_0, w_1,w_2\}$. Then ![]() ${\mathcal {F}}$ is a normal family. If
${\mathcal {F}}$ is a normal family. If ![]() $f$ is a limit of a sequence in
$f$ is a limit of a sequence in ![]() ${\mathcal {F}}$ then
${\mathcal {F}}$ then ![]() $f(z_i) = w_i$ for
$f(z_i) = w_i$ for ![]() $z_i \in {\mathbb {H}}^2$ and if
$z_i \in {\mathbb {H}}^2$ and if ![]() $f$ is non-constant then
$f$ is non-constant then ![]() $f(z_i) = w_i$ for all
$f(z_i) = w_i$ for all ![]() $i=0,1,2$.
$i=0,1,2$.
For ![]() $s \in \mathbb {R}$ we say that
$s \in \mathbb {R}$ we say that ![]() $\phi \in {\mathcal {U}}$ is
$\phi \in {\mathcal {U}}$ is ![]() $s$-invariant if it is invariant under the isometry
$s$-invariant if it is invariant under the isometry ![]() $z\mapsto e^sz$ (as a quadratic differential). Let
$z\mapsto e^sz$ (as a quadratic differential). Let ![]() ${\mathcal {U}}_\mathbb {Z}\subset {\mathcal {U}}$ be the subspace of quadratic differentials that are
${\mathcal {U}}_\mathbb {Z}\subset {\mathcal {U}}$ be the subspace of quadratic differentials that are ![]() $s$-invariant for some
$s$-invariant for some ![]() $s \neq 0$. We can define a function
$s \neq 0$. We can define a function
by taking ![]() $\ell (\phi )$ to be the infimum over all positive
$\ell (\phi )$ to be the infimum over all positive ![]() $s$ where
$s$ where ![]() $\phi$ is
$\phi$ is ![]() $s$-invariant. Note that if
$s$-invariant. Note that if ![]() $s_n \to s$ and
$s_n \to s$ and ![]() $\phi _n$ are
$\phi _n$ are ![]() $s_n$-invariant then if
$s_n$-invariant then if ![]() $\phi _n\to \phi$ we have that
$\phi _n\to \phi$ we have that ![]() $\phi$ is
$\phi$ is ![]() $s$-invariant. This implies that
$s$-invariant. This implies that ![]() $\ell$ is continuous on
$\ell$ is continuous on ![]() ${\mathcal {U}}_\mathbb {Z}$. It is possible that
${\mathcal {U}}_\mathbb {Z}$. It is possible that ![]() $\ell (\phi ) =0$ and we let
$\ell (\phi ) =0$ and we let ![]() ${\mathcal {U}}^0_\mathbb {Z} = \ell ^{-1}(0)$. This space will be of particular interest.
${\mathcal {U}}^0_\mathbb {Z} = \ell ^{-1}(0)$. This space will be of particular interest.
Lemma 4.2 If ![]() $\phi \in {\mathcal {U}}^0_\mathbb {Z}$ then
$\phi \in {\mathcal {U}}^0_\mathbb {Z}$ then
with ![]() $|c-1|\le 1$. If
$|c-1|\le 1$. If ![]() $c\neq 0$ let
$c\neq 0$ let ![]() $g_c(z) = z^c/i^c$. If
$g_c(z) = z^c/i^c$. If ![]() $c= 0$ let
$c= 0$ let ![]() $g_c = \log z$. Then
$g_c = \log z$. Then ![]() $\phi = S(g_c)$.
$\phi = S(g_c)$.
Proof. If ![]() $\ell (\phi ) = 0$ then
$\ell (\phi ) = 0$ then ![]() $\phi$ is
$\phi$ is ![]() $s_n$-invariant for a sequence of
$s_n$-invariant for a sequence of ![]() $s_n>0$ with
$s_n>0$ with ![]() $s_n\to 0$. If
$s_n\to 0$. If ![]() $\phi$ is
$\phi$ is ![]() $s$-invariant then
$s$-invariant then ![]() $\phi$ is
$\phi$ is ![]() $sk$-invariant for all
$sk$-invariant for all ![]() $k \in \mathbb {Z}$. Together this implies that
$k \in \mathbb {Z}$. Together this implies that ![]() $\phi$ is
$\phi$ is ![]() $s$-invariant for a dense set of
$s$-invariant for a dense set of ![]() $s \in \mathbb {R}$ so by continuity
$s \in \mathbb {R}$ so by continuity ![]() $\phi$ is
$\phi$ is ![]() $s$-invariant for all
$s$-invariant for all ![]() $s\in \mathbb {R}$. From this invariance we see that if
$s\in \mathbb {R}$. From this invariance we see that if ![]() $\phi (i) = -C \,dz^2$ for some
$\phi (i) = -C \,dz^2$ for some ![]() $C \in \mathbb {C}$ then
$C \in \mathbb {C}$ then ![]() $\phi (it) = -(C/{t^2}) \,dz^2$ for all
$\phi (it) = -(C/{t^2}) \,dz^2$ for all ![]() $t>0$. As
$t>0$. As ![]() $\phi$ is holomorphic this implies that
$\phi$ is holomorphic this implies that ![]() $\phi (z) = {C}/{z^2}\,dz^2$.
$\phi (z) = {C}/{z^2}\,dz^2$.
A direct computation gives that ![]() $S(g_c) = (({1-c^2})/{2})\cdot ({dz^2}/{z^2})$. We will show that
$S(g_c) = (({1-c^2})/{2})\cdot ({dz^2}/{z^2})$. We will show that ![]() $g_c$ is univalent exactly when
$g_c$ is univalent exactly when ![]() $|c-1|\le 1$. We can write
$|c-1|\le 1$. We can write ![]() $g_c(z) = e^{c\log z}/i^c$. Let
$g_c(z) = e^{c\log z}/i^c$. Let ![]() ${\mathcal {S}}$ be the open horizontal strip in
${\mathcal {S}}$ be the open horizontal strip in ![]() $\mathbb {C}$ between the lines
$\mathbb {C}$ between the lines ![]() $\operatorname {Im} z = 0$ and
$\operatorname {Im} z = 0$ and ![]() $\operatorname {Im} z = \pi$ and let
$\operatorname {Im} z = \pi$ and let ![]() ${\mathcal {S}}_c = \{cz\ |\ z\in {\mathcal {S}}\}$. Then the image of
${\mathcal {S}}_c = \{cz\ |\ z\in {\mathcal {S}}\}$. Then the image of ![]() ${\mathbb {H}}^2$ (as the upper half-plane) under the map
${\mathbb {H}}^2$ (as the upper half-plane) under the map ![]() $z\mapsto c\log z$ is
$z\mapsto c\log z$ is ![]() ${\mathcal {S}}_c$. The exponential map restricted to
${\mathcal {S}}_c$. The exponential map restricted to ![]() ${\mathcal {S}}_c$ is injective exactly when vertical lines in
${\mathcal {S}}_c$ is injective exactly when vertical lines in ![]() $\mathbb {C}$ intersect
$\mathbb {C}$ intersect ![]() ${\mathcal {S}}_c$ in a segment of length
${\mathcal {S}}_c$ in a segment of length ![]() $<2\pi$. The intersection of a vertical line with
$<2\pi$. The intersection of a vertical line with ![]() ${\mathcal {S}}_c$ has length
${\mathcal {S}}_c$ has length ![]() $|c|\pi /\cos (\theta )$ where
$|c|\pi /\cos (\theta )$ where ![]() $\theta = \arg (c)$. Thus, we have univalence if
$\theta = \arg (c)$. Thus, we have univalence if ![]() $|c| \leq 2\cos (\theta ) = 2\operatorname {Re}(c)/|c|$, giving
$|c| \leq 2\cos (\theta ) = 2\operatorname {Re}(c)/|c|$, giving ![]() $|c|^2-2\operatorname {Re}(c) \leq 0$. Completing the square, we get
$|c|^2-2\operatorname {Re}(c) \leq 0$. Completing the square, we get ![]() $|c-1|^2\leq 1$.
$|c-1|^2\leq 1$.
The invariance of the quadratic differentials ![]() $\phi \in {\mathcal {U}}_\mathbb {Z}$ implies invariance for any univalent map
$\phi \in {\mathcal {U}}_\mathbb {Z}$ implies invariance for any univalent map ![]() $f$ with
$f$ with ![]() $S(f) = \phi$. The next lemma makes this precise.
$S(f) = \phi$. The next lemma makes this precise.
Lemma 4.3 If the quadratic differential ![]() $\phi \in {\mathcal {U}}_\mathbb {Z}$ is
$\phi \in {\mathcal {U}}_\mathbb {Z}$ is ![]() $s$-invariant and
$s$-invariant and ![]() $f\colon {\mathbb {H}}^2\to \mathbb {C}$ is univalent with
$f\colon {\mathbb {H}}^2\to \mathbb {C}$ is univalent with ![]() $S(f) = \phi$ then there exists a
$S(f) = \phi$ then there exists a ![]() $\psi \in {\rm PSL}(2,\mathbb {C})$ with
$\psi \in {\rm PSL}(2,\mathbb {C})$ with ![]() $\psi \circ f(z) = f(e^s z)$. Furthermore,
$\psi \circ f(z) = f(e^s z)$. Furthermore, ![]() $\psi$ is either loxodromic or parabolic and
$\psi$ is either loxodromic or parabolic and ![]() $f$ extends continuously to
$f$ extends continuously to ![]() $0$ and
$0$ and ![]() $\infty$, with
$\infty$, with ![]() $f(0)$ the repelling fixed point of
$f(0)$ the repelling fixed point of ![]() $\psi$ and
$\psi$ and ![]() $f(\infty )$ the attracting fixed point if
$f(\infty )$ the attracting fixed point if ![]() $\psi$ is loxodromic and
$\psi$ is loxodromic and ![]() $f(0) = f(\infty )$ if
$f(0) = f(\infty )$ if ![]() $\psi$ is parabolic.
$\psi$ is parabolic.
Proof. If ![]() $\phi$ is
$\phi$ is ![]() $s$-invariant and
$s$-invariant and ![]() $f$ is a univalent map with
$f$ is a univalent map with ![]() $\phi = S(f)$ then the map
$\phi = S(f)$ then the map ![]() $z\mapsto f(e^s z)$ also has Schwarzian
$z\mapsto f(e^s z)$ also has Schwarzian ![]() $\phi$. As two maps with the same Schwarzian differ by post-composition of an element of
$\phi$. As two maps with the same Schwarzian differ by post-composition of an element of ![]() ${\rm PSL}(2,\mathbb {C})$ we have that there exists a
${\rm PSL}(2,\mathbb {C})$ we have that there exists a ![]() $\psi \in {\rm PSL}(2,\mathbb {C})$ with
$\psi \in {\rm PSL}(2,\mathbb {C})$ with ![]() $\psi \circ f(z) = f(e^s z)$. Iterating this formula, for any positive integer
$\psi \circ f(z) = f(e^s z)$. Iterating this formula, for any positive integer ![]() $k$ we have that
$k$ we have that ![]() $\psi ^k\circ f(z) = f(e^{sk}z)$. This implies that
$\psi ^k\circ f(z) = f(e^{sk}z)$. This implies that ![]() $f({\mathbb {H}}^2)$ is
$f({\mathbb {H}}^2)$ is ![]() $\psi$-invariant and that the action of
$\psi$-invariant and that the action of ![]() $\psi$ on the simply connected space
$\psi$ on the simply connected space ![]() $f({\mathbb {H}}^2)$ does not have fixed points so
$f({\mathbb {H}}^2)$ does not have fixed points so ![]() $\psi$ must be loxodromic or parabolic. Furthermore, the equation
$\psi$ must be loxodromic or parabolic. Furthermore, the equation ![]() $\psi ^k\circ f(z) = f(e^{sk}z)$ implies that
$\psi ^k\circ f(z) = f(e^{sk}z)$ implies that ![]() $f$ extends continuously to
$f$ extends continuously to ![]() $0$ and
$0$ and ![]() $\infty$ with
$\infty$ with ![]() $f(0)$ the repelling fixed point of
$f(0)$ the repelling fixed point of ![]() $\psi$ and
$\psi$ and ![]() $f(\infty )$ the attracting fixed point.
$f(\infty )$ the attracting fixed point.
The element ![]() $\psi$ is the holonomy of
$\psi$ is the holonomy of ![]() $\phi$. Let
$\phi$. Let ![]() ${\mathcal {U}}^+_\mathbb {Z} \subset {\mathcal {U}}_\mathbb {Z}$ be the subspace of quadratic differentials
${\mathcal {U}}^+_\mathbb {Z} \subset {\mathcal {U}}_\mathbb {Z}$ be the subspace of quadratic differentials ![]() $\phi$ where
$\phi$ where ![]() $\ell (\phi ) >0$ and the holonomy is loxodromic. For
$\ell (\phi ) >0$ and the holonomy is loxodromic. For ![]() $\phi \in {\mathcal {U}}^+_\mathbb {Z}$ we define a complex length function
$\phi \in {\mathcal {U}}^+_\mathbb {Z}$ we define a complex length function ![]() ${\mathcal {L}}\colon {\mathcal {U}}^+_\mathbb {Z}\to \mathbb {C}$ as follows. Let
${\mathcal {L}}\colon {\mathcal {U}}^+_\mathbb {Z}\to \mathbb {C}$ as follows. Let ![]() $f\colon {\mathbb {H}}^2\to \mathbb {C}$ be a univalent map with
$f\colon {\mathbb {H}}^2\to \mathbb {C}$ be a univalent map with ![]() $f(0) = 0$,
$f(0) = 0$, ![]() $f(\infty ) = \infty$ and
$f(\infty ) = \infty$ and ![]() $S(f) = \phi$. Choose a logarithm,
$S(f) = \phi$. Choose a logarithm, ![]() $\log _\phi$, on
$\log _\phi$, on ![]() $f({\mathbb {H}}^2)$. We then define
$f({\mathbb {H}}^2)$. We then define ![]() ${\mathcal {L}}(\phi ) = \log _\phi (f(e^{\ell (\phi )}z)) - \log _\phi (f(z))$. The expression on the right is independent of the choice of
${\mathcal {L}}(\phi ) = \log _\phi (f(e^{\ell (\phi )}z)) - \log _\phi (f(z))$. The expression on the right is independent of the choice of ![]() $f$, the choice of
$f$, the choice of ![]() $z \in {\mathbb {H}}^2$, and the choice of logarithm.
$z \in {\mathbb {H}}^2$, and the choice of logarithm.
We also define a function ![]() $c\colon {\mathcal {U}}_\mathbb {Z}^+\to \mathbb {C}$ by
$c\colon {\mathcal {U}}_\mathbb {Z}^+\to \mathbb {C}$ by
Lemma 4.4 The function ![]() $c$ extends continuously to
$c$ extends continuously to ![]() ${\mathcal {U}}^0_\mathbb {Z}$, and for
${\mathcal {U}}^0_\mathbb {Z}$, and for ![]() $\phi \in {\mathcal {U}}^0_\mathbb {Z}$ we have
$\phi \in {\mathcal {U}}^0_\mathbb {Z}$ we have
Proof. If ![]() $f$ is univalent and
$f$ is univalent and ![]() $S(f)=\phi \in {\mathcal {U}}^+_\mathbb {Z}$ then we have the Bers inequality (or McMullen's interpretation of the Bers inequality [Reference McMullenMcM90, Proposition 6.4]):
$S(f)=\phi \in {\mathcal {U}}^+_\mathbb {Z}$ then we have the Bers inequality (or McMullen's interpretation of the Bers inequality [Reference McMullenMcM90, Proposition 6.4]):
The statement is usually made in the context of quasifuchsian groups, but the proof goes through without change in our setting. From this we see that
 \begin{align*} |c(\phi)|^2 = \frac{|\mathcal{L}(\phi)|^2}{\ell(\phi)^2} &\leq 2\operatorname{Re}\biggl(\frac{\mathcal{L}(\phi)}{\ell(\phi)}\biggr) = 2\operatorname{Re}(c(\phi)),\\ |c(\phi)|^2-2\operatorname{Re}(c(\phi)) &\leq 0, \\ |c(\phi) - 1|^2-1 &\leq 0. \end{align*}
\begin{align*} |c(\phi)|^2 = \frac{|\mathcal{L}(\phi)|^2}{\ell(\phi)^2} &\leq 2\operatorname{Re}\biggl(\frac{\mathcal{L}(\phi)}{\ell(\phi)}\biggr) = 2\operatorname{Re}(c(\phi)),\\ |c(\phi)|^2-2\operatorname{Re}(c(\phi)) &\leq 0, \\ |c(\phi) - 1|^2-1 &\leq 0. \end{align*}
Thus, ![]() $|c(\phi )-1| \leq 1$.
$|c(\phi )-1| \leq 1$.
Now assume ![]() $\phi \in {\mathcal {U}}_\mathbb {Z}^0$. Then by Lemma 4.3 we have
$\phi \in {\mathcal {U}}_\mathbb {Z}^0$. Then by Lemma 4.3 we have ![]() $\phi = C({dz^2}/{z^2})$ for some
$\phi = C({dz^2}/{z^2})$ for some ![]() $C \in \mathbb {C}$. Take a sequence
$C \in \mathbb {C}$. Take a sequence ![]() $\phi _n$ in
$\phi _n$ in ![]() ${\mathcal {U}}_\mathbb {Z}^+$ with
${\mathcal {U}}_\mathbb {Z}^+$ with ![]() $\phi _n \to \phi$ and let
$\phi _n \to \phi$ and let ![]() $\ell _n = \ell (\phi _n)$,
$\ell _n = \ell (\phi _n)$, ![]() ${\mathcal {L}}_n = {\mathcal {L}}(\phi _n)$, and
${\mathcal {L}}_n = {\mathcal {L}}(\phi _n)$, and ![]() $c_n = c(\phi _n)$. Since
$c_n = c(\phi _n)$. Since ![]() $\ell$ is continuous on
$\ell$ is continuous on ![]() ${\mathcal {U}}_\mathbb {Z}$ we have that
${\mathcal {U}}_\mathbb {Z}$ we have that ![]() $\ell _n\to 0$ and we can choose integers
$\ell _n\to 0$ and we can choose integers ![]() $k_n$ such that
$k_n$ such that ![]() $k_n\ell _n\to 1$. We also fix univalent maps
$k_n\ell _n\to 1$. We also fix univalent maps ![]() $f_n$ with
$f_n$ with ![]() $S(f_n) = \phi _n$ and the normalization
$S(f_n) = \phi _n$ and the normalization ![]() $f_n(\infty ) = \infty$,
$f_n(\infty ) = \infty$, ![]() $f_n(i) =0$, and
$f_n(i) =0$, and ![]() $f_n(ie) = 1$. By Theorem 4.1 the
$f_n(ie) = 1$. By Theorem 4.1 the ![]() $f_n$ will be a normal family. Let
$f_n$ will be a normal family. Let ![]() $f$ be a limit of a subsequence of the
$f$ be a limit of a subsequence of the ![]() $f_n$. Again by Theorem 4.1,
$f_n$. Again by Theorem 4.1, ![]() $f(i) =0$ and
$f(i) =0$ and ![]() $f(ie) =1$ so the limit will not be constant, which in turn implies that
$f(ie) =1$ so the limit will not be constant, which in turn implies that ![]() $f(\infty ) = \infty$ and that
$f(\infty ) = \infty$ and that ![]() $f$ is univalent. It follows that
$f$ is univalent. It follows that ![]() $S(f_n) = \phi _n \to \phi = S(f)$. As
$S(f_n) = \phi _n \to \phi = S(f)$. As ![]() $f$ is the only map with
$f$ is the only map with ![]() $S(f) = \phi$ plus the given normalization, any convergent subsequence of the
$S(f) = \phi$ plus the given normalization, any convergent subsequence of the ![]() $f_n$ will converge to
$f_n$ will converge to ![]() $f$. Therefore,
$f$. Therefore, ![]() $f_n$ converges to
$f_n$ converges to ![]() $f$ (uniformly on compact sets) without passing to a subsequence.
$f$ (uniformly on compact sets) without passing to a subsequence.
If ![]() $\psi _n$ is the element of
$\psi _n$ is the element of ![]() ${\rm PSL}(2,\mathbb {C})$ with
${\rm PSL}(2,\mathbb {C})$ with ![]() $f_n(e^{\ell _n}z) = \psi _n\circ f_n(z)$ then the attracting fixed point of
$f_n(e^{\ell _n}z) = \psi _n\circ f_n(z)$ then the attracting fixed point of ![]() $\psi _n$ and all its powers is
$\psi _n$ and all its powers is ![]() $\infty$. Therefore,
$\infty$. Therefore, ![]() $\psi _n^{k_n}(z)= e^{k_n {\mathcal {L}}_n} z + A_n$ for some
$\psi _n^{k_n}(z)= e^{k_n {\mathcal {L}}_n} z + A_n$ for some ![]() $A_n \in \mathbb {C}$. As
$A_n \in \mathbb {C}$. As ![]() $c_n$ lies in a compact set we can pass to a subsequence such that
$c_n$ lies in a compact set we can pass to a subsequence such that ![]() $c_n \to b$ and therefore
$c_n \to b$ and therefore ![]() $k_n{\mathcal {L}}_n = k_n\ell _n c_n \to b$. Taking the limit of the equation
$k_n{\mathcal {L}}_n = k_n\ell _n c_n \to b$. Taking the limit of the equation ![]() $f_n(e^{k_n\ell _n}z) = e^{k_n{\mathcal {L}}_n}f_n(z) + A_n$, we have
$f_n(e^{k_n\ell _n}z) = e^{k_n{\mathcal {L}}_n}f_n(z) + A_n$, we have
Substituting in ![]() $i$, for
$i$, for ![]() $z$ we see that
$z$ we see that ![]() $A_n\to 1$. It follows that
$A_n\to 1$. It follows that ![]() $e^b$ is determined by
$e^b$ is determined by ![]() $f$ (and hence
$f$ (and hence ![]() $\phi$). This determines
$\phi$). This determines ![]() $b$ up to a multiple of
$b$ up to a multiple of ![]() $2\pi i$. However, we also have
$2\pi i$. However, we also have ![]() $|b-1| \le 1$, which implies that
$|b-1| \le 1$, which implies that ![]() $-1\le \operatorname {Im} b \le 1$, so the equation uniquely determines
$-1\le \operatorname {Im} b \le 1$, so the equation uniquely determines ![]() $b$. In particular,
$b$. In particular, ![]() $c_n\to b$ before passing to a subsequence.
$c_n\to b$ before passing to a subsequence.
Let ![]() $g_c$ be the univalent map given by Lemma 4.2 with
$g_c$ be the univalent map given by Lemma 4.2 with ![]() $S(g_c) = \phi$. Then
$S(g_c) = \phi$. Then ![]() $g_c = \beta \circ f$ for some
$g_c = \beta \circ f$ for some ![]() $\beta \in {\rm PSL}(2,\mathbb {C})$. Note that
$\beta \in {\rm PSL}(2,\mathbb {C})$. Note that ![]() $\psi ^{k_n}_n \to \psi$ in
$\psi ^{k_n}_n \to \psi$ in ![]() ${\rm PSL}(2,\mathbb {C})$ with
${\rm PSL}(2,\mathbb {C})$ with ![]() $\psi (z) = e^bz + 1$. If
$\psi (z) = e^bz + 1$. If ![]() $b=0$ then
$b=0$ then ![]() $f(0) = f(\infty ) = \infty$ so we must have that
$f(0) = f(\infty ) = \infty$ so we must have that ![]() $g_c(0) = g_c(\infty )$, and this only occurs when
$g_c(0) = g_c(\infty )$, and this only occurs when ![]() $c=0$ and
$c=0$ and ![]() $g_c(z) = \log z$. If
$g_c(z) = \log z$. If ![]() $b\neq 0$ then the repelling and attracting fixed points of
$b\neq 0$ then the repelling and attracting fixed points of ![]() $\beta \circ \psi \circ \beta ^{-1}$ are
$\beta \circ \psi \circ \beta ^{-1}$ are ![]() $g_c(0) = 0$ and
$g_c(0) = 0$ and ![]() $g_c(\infty ) = \infty$. This implies that
$g_c(\infty ) = \infty$. This implies that ![]() $\beta \circ \psi \circ \beta ^{-1}(z) = e^b z$ and
$\beta \circ \psi \circ \beta ^{-1}(z) = e^b z$ and ![]() $g_c(ez) = e^bg_c(z)$. It follows that
$g_c(ez) = e^bg_c(z)$. It follows that ![]() $b=c$. In both cases we can define
$b=c$. In both cases we can define ![]() $c(\phi ) = \lim _{n\to \infty } c_n$ and we have that
$c(\phi ) = \lim _{n\to \infty } c_n$ and we have that ![]() $c$ extends continuously to
$c$ extends continuously to ![]() ${\mathcal {U}}_\mathbb {Z}^0$ with
${\mathcal {U}}_\mathbb {Z}^0$ with
We now describe the map from ![]() $CC(N;S,X)$ to
$CC(N;S,X)$ to ![]() ${\mathcal {U}}^+_\mathbb {Z} \subset {\mathcal {U}}$. It will depend on a choice of essential closed curve
${\mathcal {U}}^+_\mathbb {Z} \subset {\mathcal {U}}$. It will depend on a choice of essential closed curve ![]() $\alpha$ on
$\alpha$ on ![]() $S$. Given
$S$. Given ![]() $M_Y \in CC(N;S,X)$, let
$M_Y \in CC(N;S,X)$, let ![]() $\Omega$ be a component of the domain of discontinuity that projects to the component of
$\Omega$ be a component of the domain of discontinuity that projects to the component of ![]() $Y$ that contains
$Y$ that contains ![]() $\alpha$. Let
$\alpha$. Let ![]() $f_Y\colon {\mathbb {H}}^2\to \Omega$ be a uniformizing univalent map that takes the imaginary axis in
$f_Y\colon {\mathbb {H}}^2\to \Omega$ be a uniformizing univalent map that takes the imaginary axis in ![]() ${\mathbb {H}}^2$ to an axis for
${\mathbb {H}}^2$ to an axis for ![]() $\alpha$ and let
$\alpha$ and let ![]() $\phi _Y = S(f_Y)$. While we have made several choices, the quadratic differential
$\phi _Y = S(f_Y)$. While we have made several choices, the quadratic differential ![]() $\phi _Y$ is independent of our choices. We can then define
$\phi _Y$ is independent of our choices. We can then define ![]() $\Psi _\alpha \colon CC(N;S,X) \to {\mathcal {U}}$ by
$\Psi _\alpha \colon CC(N;S,X) \to {\mathcal {U}}$ by ![]() $\Psi _\alpha (M_Y) = \phi _Y$. This map is continuous and
$\Psi _\alpha (M_Y) = \phi _Y$. This map is continuous and ![]() $\ell _\alpha = \ell \circ \Psi _\alpha$. Since
$\ell _\alpha = \ell \circ \Psi _\alpha$. Since ![]() $\ell _\alpha$ is positive on
$\ell _\alpha$ is positive on ![]() $CC(N;S,X)$ we have that the image of
$CC(N;S,X)$ we have that the image of ![]() $\Psi _\alpha$ lies in
$\Psi _\alpha$ lies in ![]() ${\mathcal {U}}^+_\mathbb {Z}$.
${\mathcal {U}}^+_\mathbb {Z}$.
Given ![]() $\phi \in {\mathcal {U}}$, we define
$\phi \in {\mathcal {U}}$, we define
Thus, ![]() $\mu _\phi$ is the negative of the corresponding harmonic Beltrami differential. We also let
$\mu _\phi$ is the negative of the corresponding harmonic Beltrami differential. We also let ![]() $A_s$ be the quotient of
$A_s$ be the quotient of ![]() ${\mathbb {H}}^2$ under the action
${\mathbb {H}}^2$ under the action ![]() $z\mapsto e^s z$ and
$z\mapsto e^s z$ and ![]() $\langle, \rangle _s$ the pair of quadratic differentials and Beltrami differentials on
$\langle, \rangle _s$ the pair of quadratic differentials and Beltrami differentials on ![]() $A_s$. If
$A_s$. If ![]() $\phi$ is
$\phi$ is ![]() $s$-invariant as a quadratic differential then
$s$-invariant as a quadratic differential then ![]() $\mu _\phi$ is
$\mu _\phi$ is ![]() $s$-invariant as a Beltrami differential and descends to a Beltrami differential on
$s$-invariant as a Beltrami differential and descends to a Beltrami differential on ![]() $A_s$. We define a function
$A_s$. We define a function
by
 \[ F_\ell(\phi) = \frac{2}{\pi\ell(\phi)} \operatorname{Re} \biggl\langle \mu_\phi, \frac{dz^2}{z^2}\biggr\rangle_{\ell(\phi)}. \]
\[ F_\ell(\phi) = \frac{2}{\pi\ell(\phi)} \operatorname{Re} \biggl\langle \mu_\phi, \frac{dz^2}{z^2}\biggr\rangle_{\ell(\phi)}. \]
As an immediate consequence of Gardiner's formula (Theorem 2.1) we have the following lemma.
Lemma 4.5
Therefore, to study the continuity of ![]() $d\ell _\alpha (V)$ we will study the continuity of
$d\ell _\alpha (V)$ we will study the continuity of ![]() $F_\ell$ on
$F_\ell$ on ![]() ${\mathcal {U}}_\mathbb {Z}$.
${\mathcal {U}}_\mathbb {Z}$.
Lemma 4.6 The function ![]() $F_\ell$ extends continuously to
$F_\ell$ extends continuously to ![]() ${\mathcal {U}}^0_\mathbb {Z}$ with
${\mathcal {U}}^0_\mathbb {Z}$ with
for ![]() $\phi \in {\mathcal {U}}^0_\mathbb {Z}$.
$\phi \in {\mathcal {U}}^0_\mathbb {Z}$.
Proof. The key to the proof is that if ![]() $\mu$ and
$\mu$ and ![]() $\psi$ are
$\psi$ are ![]() $s$-invariant then
$s$-invariant then ![]() $\langle \mu, \psi \rangle _{sk} = k\langle \mu, \psi \rangle _s$ for all positive integers
$\langle \mu, \psi \rangle _{sk} = k\langle \mu, \psi \rangle _s$ for all positive integers ![]() $k$. Then if
$k$. Then if ![]() $\phi _n \to \phi$ for
$\phi _n \to \phi$ for ![]() $\phi \in {\mathcal {U}}^0_\mathbb {Z}$ we can choose
$\phi \in {\mathcal {U}}^0_\mathbb {Z}$ we can choose ![]() $k_n$ such that
$k_n$ such that ![]() $k_n\ell (\phi _n) \to 1$ so that
$k_n\ell (\phi _n) \to 1$ so that
 \begin{align*} F_\ell(\phi_n) & = \frac{2}{\pi\ell(\phi)} \operatorname{Re}\biggl\langle \mu_{\phi_n}, \frac{dz^2}{z^2} \biggr\rangle_{\ell(\phi_n)}\\ & = \frac2\pi \operatorname{Re}\biggl\langle \frac{1}{k_n\ell(\phi_n)} \mu_{\phi_n}, \frac{dz^2}{z^2}\biggr\rangle_{k_n\ell(\phi_n)}\\ &\longrightarrow \frac2\pi \operatorname{Re}\biggl\langle \mu_\phi, \frac{dz^2}{z^2} \biggr\rangle_1. \end{align*}
\begin{align*} F_\ell(\phi_n) & = \frac{2}{\pi\ell(\phi)} \operatorname{Re}\biggl\langle \mu_{\phi_n}, \frac{dz^2}{z^2} \biggr\rangle_{\ell(\phi_n)}\\ & = \frac2\pi \operatorname{Re}\biggl\langle \frac{1}{k_n\ell(\phi_n)} \mu_{\phi_n}, \frac{dz^2}{z^2}\biggr\rangle_{k_n\ell(\phi_n)}\\ &\longrightarrow \frac2\pi \operatorname{Re}\biggl\langle \mu_\phi, \frac{dz^2}{z^2} \biggr\rangle_1. \end{align*}
This shows that the ![]() $F_\ell$ extends continuously to
$F_\ell$ extends continuously to ![]() ${\mathcal {U}}_\mathbb {Z}^0$.
${\mathcal {U}}_\mathbb {Z}^0$.
For ![]() $\phi \in {\mathcal {U}}^0_\mathbb {Z}$ we have
$\phi \in {\mathcal {U}}^0_\mathbb {Z}$ we have ![]() $\phi (z) = (({1-c(\phi )^2})/2) \cdot ({dz^2}/{z^2})$. The pairing is easier to calculate in the strip model for
$\phi (z) = (({1-c(\phi )^2})/2) \cdot ({dz^2}/{z^2})$. The pairing is easier to calculate in the strip model for ![]() ${\mathbb {H}}^2$ (the region
${\mathbb {H}}^2$ (the region ![]() ${\mathcal {S}}$ between the horizontal lines
${\mathcal {S}}$ between the horizontal lines ![]() $\operatorname {Im} z =0$ and
$\operatorname {Im} z =0$ and ![]() $\operatorname {Im} z= \pi$) with area form
$\operatorname {Im} z= \pi$) with area form ![]() $\rho _{\mathbb {H}}^2 = 1/\sin ^2 y$. In this model the quadratic differential
$\rho _{\mathbb {H}}^2 = 1/\sin ^2 y$. In this model the quadratic differential ![]() $dz^2/z^2$ becomes
$dz^2/z^2$ becomes ![]() $dz^2$ so
$dz^2$ so ![]() $\mu _\phi (z) = \sin ^2y (\overline {c(\phi )}^2-1)/2$ and
$\mu _\phi (z) = \sin ^2y (\overline {c(\phi )}^2-1)/2$ and
 \begin{align*} \biggl\langle \mu_\phi, \frac{dz^2}{z^2} \biggr\rangle_1 &= \frac{\overline{c(\phi)^2}-1}2\int_0^\pi\int_0^1 \sin^2 y \,dx\,dy\\ &= \frac{\pi\big(\overline{c(\phi)^2}-1\big)}4. \end{align*}
\begin{align*} \biggl\langle \mu_\phi, \frac{dz^2}{z^2} \biggr\rangle_1 &= \frac{\overline{c(\phi)^2}-1}2\int_0^\pi\int_0^1 \sin^2 y \,dx\,dy\\ &= \frac{\pi\big(\overline{c(\phi)^2}-1\big)}4. \end{align*}
Taking the real part and multiplying by ![]() $2/\pi$ gives the claimed formula for
$2/\pi$ gives the claimed formula for ![]() $F_\ell (\phi )$.
$F_\ell (\phi )$.
We would like to similarly define a function on ![]() ${\mathcal {U}}^+_\mathbb {Z}$ for the differential
${\mathcal {U}}^+_\mathbb {Z}$ for the differential ![]() $d\log {\mathcal {L}}_\alpha$. We will not be able to do this exactly but instead give a formula for the central term. We will need to evaluate the auxiliary term separately.
$d\log {\mathcal {L}}_\alpha$. We will not be able to do this exactly but instead give a formula for the central term. We will need to evaluate the auxiliary term separately.
Given ![]() $\phi \in {\mathcal {U}}^+_\mathbb {Z}$, let
$\phi \in {\mathcal {U}}^+_\mathbb {Z}$, let ![]() $g_\phi \colon {\mathbb {H}}^2\to \mathbb {C}$ be the univalent map with
$g_\phi \colon {\mathbb {H}}^2\to \mathbb {C}$ be the univalent map with ![]() $S(g_\phi ) = \phi$ and
$S(g_\phi ) = \phi$ and ![]() $g_\phi (0) =0$,
$g_\phi (0) =0$, ![]() $g_\phi (\infty ) =\infty$, and
$g_\phi (\infty ) =\infty$, and ![]() $g_\phi (i) = i$. By Theorem 4.1, this is a normal family. We observe that if
$g_\phi (i) = i$. By Theorem 4.1, this is a normal family. We observe that if ![]() $\phi$ is
$\phi$ is ![]() $s$-invariant the quadratic differential
$s$-invariant the quadratic differential ![]() $(g_\phi )^* ({dz^2}/{z^2})$ is
$(g_\phi )^* ({dz^2}/{z^2})$ is ![]() $s$-invariant. We then define a function
$s$-invariant. We then define a function
by
 \[ F_{\mathcal{L}}(\phi) = \frac1{\pi{\mathcal{L}}(\phi)} \biggl\langle \mu_\phi, (g_\phi)^*\biggl(\frac{dz^2}{z^2}\biggr)\biggr\rangle_{\ell(\phi)}. \]
\[ F_{\mathcal{L}}(\phi) = \frac1{\pi{\mathcal{L}}(\phi)} \biggl\langle \mu_\phi, (g_\phi)^*\biggl(\frac{dz^2}{z^2}\biggr)\biggr\rangle_{\ell(\phi)}. \]
From Theorem 2.2 and the discussion following it we have the following lemma.
Lemma 4.7
We now establish the continuity of ![]() $F_{\mathcal {L}}$.
$F_{\mathcal {L}}$.
Lemma 4.8 The function ![]() $F_{\mathcal {L}}$ extends continuously to
$F_{\mathcal {L}}$ extends continuously to ![]() ${\mathcal {U}}_\mathbb {Z}^0$ with
${\mathcal {U}}_\mathbb {Z}^0$ with
Proof. The proof is similar to Lemma 4.6. Assume that ![]() $\phi _n$ in
$\phi _n$ in ![]() ${\mathcal {U}}^+_\mathbb {Z}$ converges to
${\mathcal {U}}^+_\mathbb {Z}$ converges to ![]() $\phi \in {\mathcal {U}}_\mathbb {Z}^0$ and let
$\phi \in {\mathcal {U}}_\mathbb {Z}^0$ and let ![]() $g_n = g_{\phi _n}$,
$g_n = g_{\phi _n}$, ![]() $\ell _n = \ell (\phi _n)$, etc. Choose integers
$\ell _n = \ell (\phi _n)$, etc. Choose integers ![]() $k_n$ with
$k_n$ with ![]() $k_n\ell _n \to 1$. By Lemma 4.4 the function
$k_n\ell _n \to 1$. By Lemma 4.4 the function ![]() $c$ is continuous and therefore
$c$ is continuous and therefore ![]() $k_n{\mathcal {L}}_n=k_n\ell _n c_n \to c(\phi )$.
$k_n{\mathcal {L}}_n=k_n\ell _n c_n \to c(\phi )$.
In Lemma 4.9 below we will show that
We assume this for now and then as in Lemma 4.6 we have
 \begin{align*} F_{{\mathcal{L}}}(\phi_n) & = \frac1\pi\biggl\langle\frac1{k_n{\mathcal{L}}_n}\mu_n, (g_n)^*\biggl(\frac{dz^2}{z^2}\biggr)\biggr\rangle_{k_n\ell_n} \\ & = \frac{c_n}\pi\biggl\langle\frac1{k_n\ell_n}\mu_n, \frac{1}{c^2_n}(g_n)^*\biggl(\frac{dz^2}{z^2}\biggr)\biggr\rangle_{k_n\ell_n}\\ &\longrightarrow \frac{c(\phi)}{\pi}\biggl\langle \mu_\phi, \frac{dz^2}{z^2}\biggr\rangle_1\\ &= \frac{c(\phi)\bigl(\overline{c(\phi)^2}-1\bigr)}{4}. \end{align*}
\begin{align*} F_{{\mathcal{L}}}(\phi_n) & = \frac1\pi\biggl\langle\frac1{k_n{\mathcal{L}}_n}\mu_n, (g_n)^*\biggl(\frac{dz^2}{z^2}\biggr)\biggr\rangle_{k_n\ell_n} \\ & = \frac{c_n}\pi\biggl\langle\frac1{k_n\ell_n}\mu_n, \frac{1}{c^2_n}(g_n)^*\biggl(\frac{dz^2}{z^2}\biggr)\biggr\rangle_{k_n\ell_n}\\ &\longrightarrow \frac{c(\phi)}{\pi}\biggl\langle \mu_\phi, \frac{dz^2}{z^2}\biggr\rangle_1\\ &= \frac{c(\phi)\bigl(\overline{c(\phi)^2}-1\bigr)}{4}. \end{align*}
Lemma 4.9
Proof. We first assume that ![]() $c(\phi ) \neq 0$. By our normalization
$c(\phi ) \neq 0$. By our normalization ![]() $g_n(e^{k_n\ell _n} z) =e^{k_n{\mathcal {L}}_n} g_n(z)$, so (after possibly passing to a subsequence) as
$g_n(e^{k_n\ell _n} z) =e^{k_n{\mathcal {L}}_n} g_n(z)$, so (after possibly passing to a subsequence) as ![]() $n\to \infty$ we have
$n\to \infty$ we have ![]() $g(ez) = e^{c(\phi )} g(z)$ where
$g(ez) = e^{c(\phi )} g(z)$ where ![]() $g_n \to g$. Since
$g_n \to g$. Since ![]() $c(\phi )\neq 0$ we have that
$c(\phi )\neq 0$ we have that ![]() $g$ is non-constant and it follows that
$g$ is non-constant and it follows that ![]() $g$ fixes
$g$ fixes ![]() $0$,
$0$, ![]() $i$, and
$i$, and ![]() $\infty$ and
$\infty$ and ![]() $S(g) = \phi$. This implies that
$S(g) = \phi$. This implies that ![]() $g(z)= e^{c(\phi )}/i^{c(\phi )}$. It follows that
$g(z)= e^{c(\phi )}/i^{c(\phi )}$. It follows that
so the lemma holds if ![]() $c(\phi ) \neq 0$.
$c(\phi ) \neq 0$.
When ![]() $c(\phi ) =0$ (and therefore, by Lemma 4.2,
$c(\phi ) =0$ (and therefore, by Lemma 4.2, ![]() $\phi = 1/2\cdot {dz^2}/{z^2}$) it will be necessary to choose a different normalization for the
$\phi = 1/2\cdot {dz^2}/{z^2}$) it will be necessary to choose a different normalization for the ![]() $g_n$ so that they do not converge to a constant function. In particular, similar to the proof of Lemma 4.4, we choose univalent functions
$g_n$ so that they do not converge to a constant function. In particular, similar to the proof of Lemma 4.4, we choose univalent functions ![]() $f_n$ with
$f_n$ with ![]() $f_n(\infty ) = \infty$,
$f_n(\infty ) = \infty$, ![]() $f_n(i) = i\pi$, and
$f_n(i) = i\pi$, and ![]() $f_n(ie) = 1+i\pi$ and whose Schwarzian is
$f_n(ie) = 1+i\pi$ and whose Schwarzian is ![]() $\phi _n$. By Theorem 4.1, the
$\phi _n$. By Theorem 4.1, the ![]() $f_n$ form a normal family. As any limiting function will be non-constant the Schwarzians
$f_n$ form a normal family. As any limiting function will be non-constant the Schwarzians ![]() $\phi _n$ will also converge to the Schwarzian of the limit. As by assumption
$\phi _n$ will also converge to the Schwarzian of the limit. As by assumption ![]() $\phi _n \to \phi$, we have that any limiting function has Schwarzian
$\phi _n \to \phi$, we have that any limiting function has Schwarzian ![]() $\phi$. The chosen normalizations of
$\phi$. The chosen normalizations of ![]() $f_n$ will also persist in the limit. Together these conditions imply that the only possible limiting function is
$f_n$ will also persist in the limit. Together these conditions imply that the only possible limiting function is ![]() $f(z) = \log z$, so
$f(z) = \log z$, so ![]() $f_n$ converges to
$f_n$ converges to ![]() $f(z) = \log z$ uniformly on compact sets.
$f(z) = \log z$ uniformly on compact sets.
Also, as in Lemma 4.4, we have the equation ![]() $f_n(e^{k_n\ell _n}z) = e^{k_n{\mathcal {L}}_n} f_n(z) + A_n$ with
$f_n(e^{k_n\ell _n}z) = e^{k_n{\mathcal {L}}_n} f_n(z) + A_n$ with ![]() $A_n \to 1$. If we choose
$A_n \to 1$. If we choose ![]() $\beta _n \in {\rm PSL}(2,\mathbb {C})$ with
$\beta _n \in {\rm PSL}(2,\mathbb {C})$ with ![]() $g_n = \beta _n \circ f_n$ then
$g_n = \beta _n \circ f_n$ then ![]() $g_n^*(dz^2/z^2) = f_n^* (\beta _n^*(dz^2/z^2))$. To calculate
$g_n^*(dz^2/z^2) = f_n^* (\beta _n^*(dz^2/z^2))$. To calculate ![]() $\beta _n^*(dz^2/z^2)$ we observe that
$\beta _n^*(dz^2/z^2)$ we observe that ![]() $\beta _n$ takes the attracting and repelling fixed points of
$\beta _n$ takes the attracting and repelling fixed points of ![]() $z\mapsto e^{k_n{\mathcal {L}}_n} z + A_n$ to the attracting and repelling fixed points of
$z\mapsto e^{k_n{\mathcal {L}}_n} z + A_n$ to the attracting and repelling fixed points of ![]() $z\mapsto e^{k_n{\mathcal {L}}_n} z$. In particular,
$z\mapsto e^{k_n{\mathcal {L}}_n} z$. In particular, ![]() $\beta _n(A_n/(1-e^{k_n{\mathcal {L}}_n})) = 0$ and
$\beta _n(A_n/(1-e^{k_n{\mathcal {L}}_n})) = 0$ and ![]() $\beta _n(\infty ) = \infty$. It follows that
$\beta _n(\infty ) = \infty$. It follows that
As ![]() $k_n{\mathcal {L}}_n = c_n k_n \ell _n \to c(\phi )\cdot 1 = 0$ this quadratic differential will converge to zero. However, if we multiply the denominator by
$k_n{\mathcal {L}}_n = c_n k_n \ell _n \to c(\phi )\cdot 1 = 0$ this quadratic differential will converge to zero. However, if we multiply the denominator by ![]() $(k_n{\mathcal {L}}_n)^2$ the denominator will converge to
$(k_n{\mathcal {L}}_n)^2$ the denominator will converge to ![]() $1$ (since
$1$ (since ![]() $A_n \to 1$) and the quadratic differential will converge to
$A_n \to 1$) and the quadratic differential will converge to ![]() $dz^2$. We further have that
$dz^2$. We further have that ![]() $k_n{\mathcal {L}}_n/c_n \to 1$ and it follows that if we divide by
$k_n{\mathcal {L}}_n/c_n \to 1$ and it follows that if we divide by ![]() $c^2_n$ we have
$c^2_n$ we have
and since ![]() $f_n \to \log z$ this gives
$f_n \to \log z$ this gives
This proves the lemma when ![]() $c(\phi ) = 0$.
$c(\phi ) = 0$.
We can now prove our limiting formulas for the derivatives of ![]() $\ell _\alpha$,
$\ell _\alpha$, ![]() ${\mathcal {L}}_\alpha$, and
${\mathcal {L}}_\alpha$, and ![]() $c_\alpha$.
$c_\alpha$.
Theorem 4.10 Let ![]() $(N;S)$ be a relatively acylindrical pair and
$(N;S)$ be a relatively acylindrical pair and ![]() $\alpha$ an essential simple closed curve in
$\alpha$ an essential simple closed curve in ![]() $S$. Let
$S$. Let ![]() $Y_n$ be a sequence in
$Y_n$ be a sequence in ![]() $\operatorname {Teich}(S)$ with the volume of
$\operatorname {Teich}(S)$ with the volume of ![]() $C(M_{Y_n})$ bounded,
$C(M_{Y_n})$ bounded, ![]() $\|V(Y_n)\|_2 \to 0$,
$\|V(Y_n)\|_2 \to 0$, ![]() $\ell _\alpha (Y_n) \to 0$, and
$\ell _\alpha (Y_n) \to 0$, and ![]() $c_\alpha (M_{Y_n}) \to c$ for some
$c_\alpha (M_{Y_n}) \to c$ for some ![]() $c \in \mathbb {C}$. Then
$c \in \mathbb {C}$. Then
(i)
 $\displaystyle {\lim _{n\to \infty }}d(\log \ell _\alpha )(V(Y_n)) = \tfrac 12\big (\operatorname {Re}\!\big (c^2\big ) - 1\big )$,
$\displaystyle {\lim _{n\to \infty }}d(\log \ell _\alpha )(V(Y_n)) = \tfrac 12\big (\operatorname {Re}\!\big (c^2\big ) - 1\big )$,(ii)
 $\displaystyle {\lim _{n\to \infty }}d(\log {\mathcal {L}}_\alpha )(V(Y_n)) = \tfrac 14 c\big (\bar c^2 -1\big )$,
$\displaystyle {\lim _{n\to \infty }}d(\log {\mathcal {L}}_\alpha )(V(Y_n)) = \tfrac 14 c\big (\bar c^2 -1\big )$,(iii)
 $\displaystyle {\lim _{n\to \infty }}dc_\alpha (V(Y_n)) = \tfrac 14\big (|c|^4 -2c\operatorname {Re}\!\big (c^2\big ) -c^2+2c\big )$.
$\displaystyle {\lim _{n\to \infty }}dc_\alpha (V(Y_n)) = \tfrac 14\big (|c|^4 -2c\operatorname {Re}\!\big (c^2\big ) -c^2+2c\big )$.
In particular, if ![]() $Y_t$ is a flowline for
$Y_t$ is a flowline for ![]() $V$,
$V$, ![]() $Y_n = Y_{t_n}$ for a sequence
$Y_n = Y_{t_n}$ for a sequence ![]() $t_n \to \infty$, and
$t_n \to \infty$, and ![]() $\ell _\alpha (Y_n)\to 0$ and
$\ell _\alpha (Y_n)\to 0$ and ![]() $c_\alpha (M_{Y_n}) \to c$, then (1)–(3) hold.
$c_\alpha (M_{Y_n}) \to c$, then (1)–(3) hold.
Proof. Combining Lemmas 4.5 and 4.6 gives (1), and (3) follows from (1) and (2).
Recalling that ![]() $V(Y_n)$ is a harmonic Beltrami differential, we will derive (2) from Lemmas 4.7 and 4.8 if we can show that
$V(Y_n)$ is a harmonic Beltrami differential, we will derive (2) from Lemmas 4.7 and 4.8 if we can show that ![]() $|J_\alpha (V(Y_n))|/\operatorname {Re} {\mathcal {L}}_\alpha (M_Y) \to 0$. This will be the proven in the next section. In particular, as
$|J_\alpha (V(Y_n))|/\operatorname {Re} {\mathcal {L}}_\alpha (M_Y) \to 0$. This will be the proven in the next section. In particular, as ![]() $\operatorname {Re}{\mathcal {L}}_\alpha (M_{Y_n}) \le 2 \ell _\alpha (Y_n)$ and
$\operatorname {Re}{\mathcal {L}}_\alpha (M_{Y_n}) \le 2 \ell _\alpha (Y_n)$ and ![]() $\ell _\alpha (Y_n) \to 0$ we have that
$\ell _\alpha (Y_n) \to 0$ we have that ![]() $\operatorname {Re}{\mathcal {L}}_\alpha (M_{Y_n}) \to 0$. By assumption
$\operatorname {Re}{\mathcal {L}}_\alpha (M_{Y_n}) \to 0$. By assumption ![]() ${{\rm Vol}_C}(M_{Y_n})$ is bounded and
${{\rm Vol}_C}(M_{Y_n})$ is bounded and ![]() $\|V(Y_n)\|_2 \to 0$. It then follows from Theorem 5.1 that
$\|V(Y_n)\|_2 \to 0$. It then follows from Theorem 5.1 that
and (2) follows.
For the last statement we only need to show that the volume of ![]() $C(M_{Y_n})$ is bounded. As
$C(M_{Y_n})$ is bounded. As ![]() $Y_t$ is a flowline for the gradient of
$Y_t$ is a flowline for the gradient of ![]() $-{{{\rm Vol}_R}}$, the negative of the renormalized volume, we have that the renormalized volume is bounded. However, the difference between the renormalized volume and convex core volume is bounded by a constant depending only on the topology of the boundary and the length of the shortest compressible curve (see [Reference Bridgeman and CanaryBC17, Theorem 1.3]). This last constant is determined by
$-{{{\rm Vol}_R}}$, the negative of the renormalized volume, we have that the renormalized volume is bounded. However, the difference between the renormalized volume and convex core volume is bounded by a constant depending only on the topology of the boundary and the length of the shortest compressible curve (see [Reference Bridgeman and CanaryBC17, Theorem 1.3]). This last constant is determined by ![]() $X$ and hence is uniform on
$X$ and hence is uniform on ![]() $M_{Y_t}$. This implies that the convex core volume is bounded and the theorem follows.
$M_{Y_t}$. This implies that the convex core volume is bounded and the theorem follows.
5. Bounding the norm of the auxiliary term
This section is devoted to proving the following theorem.
Theorem 5.1 There exists ![]() $\delta _0 > 0$ such that, given
$\delta _0 > 0$ such that, given ![]() $\eta,K>0$, there exists a
$\eta,K>0$, there exists a ![]() $\delta >0$ such that the following assertion holds. Assume that
$\delta >0$ such that the following assertion holds. Assume that ![]() $Y\in \operatorname {Teich}(S)$ with
$Y\in \operatorname {Teich}(S)$ with ![]() ${{\rm Vol}_C}(M_Y) \le K$. Let
${{\rm Vol}_C}(M_Y) \le K$. Let ![]() $\mu \in T_Y\operatorname {Teich}(S)$ be a harmonic Beltrami differential
$\mu \in T_Y\operatorname {Teich}(S)$ be a harmonic Beltrami differential ![]() $\|\mu \|_\infty \le 3/2$ and
$\|\mu \|_\infty \le 3/2$ and ![]() $\alpha$ an essential closed curve on
$\alpha$ an essential closed curve on ![]() $S$ with
$S$ with ![]() $\|\mu \|_2 < \delta$ and
$\|\mu \|_2 < \delta$ and ![]() $\operatorname {Re}{\mathcal {L}}_\alpha (M_Y) \le \delta _0$. Then
$\operatorname {Re}{\mathcal {L}}_\alpha (M_Y) \le \delta _0$. Then
Note that the bound of ![]() $3/2$ on
$3/2$ on ![]() $\|\mu \|_\infty$ is essentially arbitrary. We have chosen it because that is the bound that we get when
$\|\mu \|_\infty$ is essentially arbitrary. We have chosen it because that is the bound that we get when ![]() $\mu$ is the harmonic Beltrami differential associated to the Schwarzian quadratic differential
$\mu$ is the harmonic Beltrami differential associated to the Schwarzian quadratic differential ![]() $\phi _Y$.
$\phi _Y$.
Recall that ![]() $J_\alpha (\mu )$ is the pairing of a Beltrami differential and a quadratic differential. The absolute value of the quadratic differential is a Euclidean area form and one can bound the pairing by bounding the norm of the quadratic differential and the area of the quadratic differential. Typically, to show that a product of two terms is small, one finds a uniform bound on one term and shows that the other term is small. To get the necessary bound here we will need to decompose
$J_\alpha (\mu )$ is the pairing of a Beltrami differential and a quadratic differential. The absolute value of the quadratic differential is a Euclidean area form and one can bound the pairing by bounding the norm of the quadratic differential and the area of the quadratic differential. Typically, to show that a product of two terms is small, one finds a uniform bound on one term and shows that the other term is small. To get the necessary bound here we will need to decompose ![]() $\mu$ into two parts. In one the norm will be small, while in the other the support will be small while the norm will only be bounded. In particular, write
$\mu$ into two parts. In one the norm will be small, while in the other the support will be small while the norm will only be bounded. In particular, write ![]() $\mu$ as
$\mu$ as
where the support of ![]() $\mu ^{<\epsilon }$ is the
$\mu ^{<\epsilon }$ is the ![]() $\epsilon$-thin part of
$\epsilon$-thin part of ![]() $Y$ and the support of
$Y$ and the support of ![]() $\mu ^{\ge \epsilon }$ is the
$\mu ^{\ge \epsilon }$ is the ![]() $\epsilon$-thick part of
$\epsilon$-thick part of ![]() $Y$. We will then bound
$Y$. We will then bound ![]() $J_\alpha (\mu ^{<\epsilon })$ and
$J_\alpha (\mu ^{<\epsilon })$ and ![]() $J_\alpha (\mu ^{\ge \epsilon })$ separately.
$J_\alpha (\mu ^{\ge \epsilon })$ separately.
Most of the work will be to bound ![]() $J_\alpha (\mu ^{<\epsilon })$, so we begin with the easier bound on
$J_\alpha (\mu ^{<\epsilon })$, so we begin with the easier bound on ![]() $J_\alpha (\mu ^{\ge \epsilon })$.
$J_\alpha (\mu ^{\ge \epsilon })$.
Lemma 5.2 Given ![]() $\epsilon, \eta >0$, there exists a
$\epsilon, \eta >0$, there exists a ![]() $\delta >0$ such that if
$\delta >0$ such that if ![]() $\|\mu \|_2 \le \delta$ then
$\|\mu \|_2 \le \delta$ then
Proof. In general, bounds on ![]() $\|\mu \|_2$ do not give bounds on
$\|\mu \|_2$ do not give bounds on ![]() $\|\mu \|_\infty$. However, a mean value estimate of Teo (see [Reference TeoTeo09]) gives bounds for points in the
$\|\mu \|_\infty$. However, a mean value estimate of Teo (see [Reference TeoTeo09]) gives bounds for points in the ![]() $\epsilon$-thick part. In particular, there exists a constant
$\epsilon$-thick part. In particular, there exists a constant ![]() $C_\epsilon >0$ such that if
$C_\epsilon >0$ such that if ![]() $z \in Y^{\ge \epsilon }$ then
$z \in Y^{\ge \epsilon }$ then ![]() $\|\mu (z)\| \le C_\epsilon \|\mu \|_2$. This implies
$\|\mu (z)\| \le C_\epsilon \|\mu \|_2$. This implies
The absolute value of the quadratic differential ![]() $dz^2/z^2$ is a Euclidean area form on
$dz^2/z^2$ is a Euclidean area form on ![]() $T_\alpha$. If we let
$T_\alpha$. If we let ![]() ${\operatorname {{\bf area}}}_\alpha$ be this area we have
${\operatorname {{\bf area}}}_\alpha$ be this area we have
and therefore
Letting ![]() $\delta = \eta /(2\pi C_\epsilon )$, the lemma follows.
$\delta = \eta /(2\pi C_\epsilon )$, the lemma follows.
To bound ![]() $J(\mu ^{<\epsilon })$ we need to bound the area of the support of
$J(\mu ^{<\epsilon })$ we need to bound the area of the support of ![]() $(\mu ^{<\epsilon })^{\rm aux}_T$. The proof of the following proposition will be most of the work of this section.
$(\mu ^{<\epsilon })^{\rm aux}_T$. The proof of the following proposition will be most of the work of this section.
Proposition 5.3 There exists ![]() $\delta _0 > 0$ such that the following assertion holds. Given
$\delta _0 > 0$ such that the following assertion holds. Given ![]() $\eta,K>0$, there exists an
$\eta,K>0$, there exists an ![]() $\epsilon >0$ such that if
$\epsilon >0$ such that if ![]() $\operatorname {Re}{\mathcal {L}}_\alpha (M_Y) \le \delta _0$ and
$\operatorname {Re}{\mathcal {L}}_\alpha (M_Y) \le \delta _0$ and ![]() ${{\rm Vol}_C}(M_Y) \le K$ then
${{\rm Vol}_C}(M_Y) \le K$ then
Assuming this for now, we can prove Theorem 5.1.
Proof of Theorem 5.1 By Proposition 5.3 we can fix an ![]() $\epsilon >0$ such that if
$\epsilon >0$ such that if ![]() $\operatorname {Re}{\mathcal {L}}_\alpha (M_Y) \le \delta _0$ and
$\operatorname {Re}{\mathcal {L}}_\alpha (M_Y) \le \delta _0$ and ![]() ${{\rm Vol}_C}(M_Y) \le K$ then
${{\rm Vol}_C}(M_Y) \le K$ then
Since ![]() $\|\mu \|_{\infty } \le 3/2$ this implies that
$\|\mu \|_{\infty } \le 3/2$ this implies that
By Lemma 5.2 we can choose ![]() $\delta >0$ such that if
$\delta >0$ such that if ![]() $\|\mu \|_2< \delta$ then
$\|\mu \|_2< \delta$ then
Note that ![]() $\delta$ depends on
$\delta$ depends on ![]() $\epsilon$ (and
$\epsilon$ (and ![]() $\eta$) but
$\eta$) but ![]() $\epsilon$ only depends on
$\epsilon$ only depends on ![]() $\eta$ and
$\eta$ and ![]() $K$. Therefore,
$K$. Therefore, ![]() $\delta$ only depends on
$\delta$ only depends on ![]() $\eta$ and
$\eta$ and ![]() $K$ and we can combine the two estimates to get the claimed bound on
$K$ and we can combine the two estimates to get the claimed bound on ![]() $|J_\alpha (\mu )|$.
$|J_\alpha (\mu )|$.
The remainder of this section is dedicated to the proof of Proposition 5.3.
5.1 Margulis tubes
Let ![]() $M$ be a hyperbolic
$M$ be a hyperbolic ![]() $n$-manifold and
$n$-manifold and ![]() $\epsilon >0$. Then we define the thick–thin decomposition
$\epsilon >0$. Then we define the thick–thin decomposition ![]() $M = M^{\leq \epsilon }\cup M^{>\epsilon }$ by
$M = M^{\leq \epsilon }\cup M^{>\epsilon }$ by
By the Margulis lemma (see [Reference ThurstonThu79]), there exists a constant ![]() $\epsilon _n$ such that for
$\epsilon _n$ such that for ![]() $\epsilon \leq \epsilon _n$ the connected components of
$\epsilon \leq \epsilon _n$ the connected components of ![]() $M^{\leq \epsilon }$ are disjoint embedded tubular neighborhoods of cusps or simple geodesics in
$M^{\leq \epsilon }$ are disjoint embedded tubular neighborhoods of cusps or simple geodesics in ![]() $M$. These tubes are called Margulis tubes and for
$M$. These tubes are called Margulis tubes and for ![]() $\alpha$ a simple closed geodesic, we denote the tube about
$\alpha$ a simple closed geodesic, we denote the tube about ![]() $\alpha$ in
$\alpha$ in ![]() $M^{\leq \epsilon }$ by
$M^{\leq \epsilon }$ by ![]() $T_\epsilon (\alpha )$. We further denote the radius of
$T_\epsilon (\alpha )$. We further denote the radius of ![]() $T_\epsilon (\alpha )$ by
$T_\epsilon (\alpha )$ by ![]() $R_\epsilon (\alpha )$.
$R_\epsilon (\alpha )$.
For hyperbolic ![]() $3$-manifolds, if
$3$-manifolds, if ![]() $\epsilon < \epsilon _3$ then by elementary hyperbolic geometry we have
$\epsilon < \epsilon _3$ then by elementary hyperbolic geometry we have
As ![]() $\partial T_\epsilon (\alpha )$ has intrinsic Euclidean metric with injectivity radius
$\partial T_\epsilon (\alpha )$ has intrinsic Euclidean metric with injectivity radius ![]() $> \epsilon$ we have the inequality
$> \epsilon$ we have the inequality
In particular,
We have the following fact due to Brooks and Matelski which gives uniform bounds on the change in ![]() $R_\epsilon (\alpha )$ as
$R_\epsilon (\alpha )$ as ![]() $\epsilon$ varies.
$\epsilon$ varies.
Theorem 5.4 (Brooks–Matelski [Reference Brooks and MatelskiBM82])
Given ![]() $\epsilon > 0$, there exist continuous functions
$\epsilon > 0$, there exist continuous functions ![]() $d^l_{\epsilon }, d^u_{\epsilon }:(0,\epsilon )\rightarrow \mathbb {R}_+$ such that
$d^l_{\epsilon }, d^u_{\epsilon }:(0,\epsilon )\rightarrow \mathbb {R}_+$ such that ![]() $d^l_{\epsilon }(\delta )\rightarrow \infty$ as
$d^l_{\epsilon }(\delta )\rightarrow \infty$ as ![]() $\delta \rightarrow 0$ and
$\delta \rightarrow 0$ and ![]() $d^u_{\epsilon }(\delta )\rightarrow 0$ as
$d^u_{\epsilon }(\delta )\rightarrow 0$ as ![]() $\delta \rightarrow \epsilon$, and for
$\delta \rightarrow \epsilon$, and for ![]() $\alpha$ a geodesic in a hyperbolic
$\alpha$ a geodesic in a hyperbolic ![]() $3$-manifold with
$3$-manifold with ![]() $\ell _\alpha (M) < \delta$ we have
$\ell _\alpha (M) < \delta$ we have
5.2 Orthogeodesics
Since ![]() $Y$ is a closed surface the components of
$Y$ is a closed surface the components of ![]() $Y^{<\epsilon }$ will be collars of closed geodesics of length
$Y^{<\epsilon }$ will be collars of closed geodesics of length ![]() $<2\epsilon$. We let
$<2\epsilon$. We let ![]() $\beta$ be one of these geodesics and
$\beta$ be one of these geodesics and ![]() ${\bf C}_\epsilon (\beta )$ the collar. Note that it is possible that
${\bf C}_\epsilon (\beta )$ the collar. Note that it is possible that ![]() $\beta =\alpha$. The pre-image of these collars in the domain of discontinuity
$\beta =\alpha$. The pre-image of these collars in the domain of discontinuity ![]() $\Omega _Y$ will be a collection of strips. Under the covering map from
$\Omega _Y$ will be a collection of strips. Under the covering map from ![]() $\mathbb {C}\smallsetminus \{0\}$ to
$\mathbb {C}\smallsetminus \{0\}$ to ![]() $T_\alpha$ most of these strips will map homeomorphically to strips. The only exception will be that there will be one component in the pre-image of the collar of
$T_\alpha$ most of these strips will map homeomorphically to strips. The only exception will be that there will be one component in the pre-image of the collar of ![]() $\alpha$ that will map to an essential annulus in
$\alpha$ that will map to an essential annulus in ![]() $T_\alpha$. This exceptional strip will be contained in the central component
$T_\alpha$. This exceptional strip will be contained in the central component ![]() $\Omega$ of
$\Omega$ of ![]() $\Omega _Y$. We only need to bound the area of the strips in
$\Omega _Y$. We only need to bound the area of the strips in ![]() $T_\alpha$. We are interested in bounding the area in
$T_\alpha$. We are interested in bounding the area in ![]() $T_\alpha$ of those strips that come from auxiliary components. To do this we will bound the area of all strips, even those coming from the central component. Our first goal is to bound the area of a single strip. We begin with some preparation.
$T_\alpha$ of those strips that come from auxiliary components. To do this we will bound the area of all strips, even those coming from the central component. Our first goal is to bound the area of a single strip. We begin with some preparation.
Associated to ![]() $\alpha$ is a solid torus cover
$\alpha$ is a solid torus cover ![]() $W_\alpha$ of
$W_\alpha$ of ![]() $M_Y$. The surface
$M_Y$. The surface ![]() $Y$ is a component of the conformal boundary of
$Y$ is a component of the conformal boundary of ![]() $M_Y$, so the
$M_Y$, so the ![]() $\epsilon$-collar of
$\epsilon$-collar of ![]() $\beta$ will lie in the conformal boundary of
$\beta$ will lie in the conformal boundary of ![]() $M_Y$ and will lift to a collection of strips in the conformal boundary of
$M_Y$ and will lift to a collection of strips in the conformal boundary of ![]() $W_\alpha$. We want to bound the area of these strips in the Euclidean metric on the conformal boundary
$W_\alpha$. We want to bound the area of these strips in the Euclidean metric on the conformal boundary ![]() $T_\alpha = \partial W_\alpha$ that comes from taking the absolute value of the quadratic differential
$T_\alpha = \partial W_\alpha$ that comes from taking the absolute value of the quadratic differential ![]() $dz^2/z^2$. Our bounds will depend on the length of
$dz^2/z^2$. Our bounds will depend on the length of ![]() $\alpha$ and the constant
$\alpha$ and the constant ![]() $\epsilon$. In the hyperbolic
$\epsilon$. In the hyperbolic ![]() $3$-manifold the closed geodesic
$3$-manifold the closed geodesic ![]() $\beta$ will lift to a collection of bi-infinite geodesics in
$\beta$ will lift to a collection of bi-infinite geodesics in ![]() $W_\alpha$ and there is a natural correspondence between the strips and these geodesics. We will see that the area of each strip decays exponentially in the distance between
$W_\alpha$ and there is a natural correspondence between the strips and these geodesics. We will see that the area of each strip decays exponentially in the distance between ![]() $\alpha$ and the corresponding lift of
$\alpha$ and the corresponding lift of ![]() $\beta$.
$\beta$.
With this informal discussion in mind we now set up the notation that we will need. Let ![]() $\bar {M}_Y$ be the union of
$\bar {M}_Y$ be the union of ![]() $M_Y$ and its conformal boundary. Then the cover
$M_Y$ and its conformal boundary. Then the cover ![]() $W_\alpha$ extends to a cover
$W_\alpha$ extends to a cover ![]() $\bar W_\alpha$ of
$\bar W_\alpha$ of ![]() $\bar {M}_Y$. Let
$\bar {M}_Y$. Let
be the covering map. We also have the nearest point projection
to the convex core. This map extends continuously to ![]() $\bar M_Y$ and lifts to a map
$\bar M_Y$ and lifts to a map
where ![]() $C(W_\alpha ) = \pi ^{-1}_\alpha (C(M_Y))$. In particular, we have
$C(W_\alpha ) = \pi ^{-1}_\alpha (C(M_Y))$. In particular, we have ![]() $r\circ \pi _\alpha = \pi _\alpha \circ r_\alpha$.
$r\circ \pi _\alpha = \pi _\alpha \circ r_\alpha$.
Now let ![]() $S^\alpha _\epsilon (\beta )$ be the collection of strips in
$S^\alpha _\epsilon (\beta )$ be the collection of strips in ![]() $\partial \bar W_\alpha$ that map to
$\partial \bar W_\alpha$ that map to ![]() ${\bf C}_\epsilon (\beta )$. If
${\bf C}_\epsilon (\beta )$. If ![]() $\beta \neq \alpha$ then this is just the union of components of
$\beta \neq \alpha$ then this is just the union of components of ![]() $\pi _\alpha ^{-1}({\bf C}_\epsilon (\beta ))$. If
$\pi _\alpha ^{-1}({\bf C}_\epsilon (\beta ))$. If ![]() $\beta =\alpha$ then there is one annular component in
$\beta =\alpha$ then there is one annular component in ![]() $\pi _\alpha ^{-1}({\bf C}_\epsilon (\alpha ))$ that is not included in
$\pi _\alpha ^{-1}({\bf C}_\epsilon (\alpha ))$ that is not included in ![]() $S^\alpha _\epsilon (\alpha )$. By [Reference Epstein, Marden and MarkovicEMM04] the retraction
$S^\alpha _\epsilon (\alpha )$. By [Reference Epstein, Marden and MarkovicEMM04] the retraction ![]() $r$ is a
$r$ is a ![]() $2$-Lipschitz map from the hyperbolic metric on
$2$-Lipschitz map from the hyperbolic metric on ![]() $Y$ to the induced path metric on
$Y$ to the induced path metric on ![]() $\partial C(M_Y)$. Therefore,
$\partial C(M_Y)$. Therefore, ![]() $r({\bf C}_\epsilon (\beta )) \subset T_{2\epsilon }(\beta )$ and if
$r({\bf C}_\epsilon (\beta )) \subset T_{2\epsilon }(\beta )$ and if ![]() ${\bf S}$ is a component of
${\bf S}$ is a component of ![]() $S^\alpha _\epsilon (\beta )$ there is a unique component
$S^\alpha _\epsilon (\beta )$ there is a unique component ![]() ${\bf T}$ of
${\bf T}$ of ![]() $\pi _\alpha ^{-1}(T_{2\epsilon }(\beta ))$ with
$\pi _\alpha ^{-1}(T_{2\epsilon }(\beta ))$ with ![]() $r_\alpha ({\bf S}) \subset {\bf T}$ (see Figure 3).
$r_\alpha ({\bf S}) \subset {\bf T}$ (see Figure 3).

Figure 3. Component ![]() ${\bf S}$ of
${\bf S}$ of ![]() $S^\alpha _\epsilon (\beta )$.
$S^\alpha _\epsilon (\beta )$.
There is a unique shortest geodesic ![]() $u$ in
$u$ in ![]() $W_\alpha$ from
$W_\alpha$ from ![]() $T_{\epsilon _3}(\alpha )$ to
$T_{\epsilon _3}(\alpha )$ to ![]() ${\bf T}$. This geodesic
${\bf T}$. This geodesic ![]() $u$ will be orthogonal to the boundary of the two tubes, so we call
$u$ will be orthogonal to the boundary of the two tubes, so we call ![]() $u$ an orthogeodesic. We will see that the area of
$u$ an orthogeodesic. We will see that the area of ![]() ${\bf S}$ decays exponentially in the length of
${\bf S}$ decays exponentially in the length of ![]() $u$. We note that while it may seem more natural to take the orthogeodesic from the geodesic
$u$. We note that while it may seem more natural to take the orthogeodesic from the geodesic ![]() $\alpha$ to the geodesic in the core of
$\alpha$ to the geodesic in the core of ![]() ${\bf T}$, for our purposes our choice of orthogeodesic is more convenient. We also emphasize that one endpoint of our orthogeodesic will always lie on the boundary of the
${\bf T}$, for our purposes our choice of orthogeodesic is more convenient. We also emphasize that one endpoint of our orthogeodesic will always lie on the boundary of the ![]() $\epsilon _3$-Margulis tube
$\epsilon _3$-Margulis tube ![]() $T_{\epsilon _3}(\alpha )$ while the other end will lie on a lift of the
$T_{\epsilon _3}(\alpha )$ while the other end will lie on a lift of the ![]() $2\epsilon$-Margulis tube
$2\epsilon$-Margulis tube ![]() $T_{2\epsilon }(\beta )$, so while our notation does not emphasize this, the orthogeodesic
$T_{2\epsilon }(\beta )$, so while our notation does not emphasize this, the orthogeodesic ![]() $u$ depends on
$u$ depends on ![]() $\epsilon$ and as
$\epsilon$ and as ![]() $\epsilon$ decreases the orthogeodesic will become longer.
$\epsilon$ decreases the orthogeodesic will become longer.
If ![]() $H$ is an embedded half-space in
$H$ is an embedded half-space in ![]() $W_\alpha$ then its closure in the conformal boundary is a round disk
$W_\alpha$ then its closure in the conformal boundary is a round disk ![]() $D$. We begin by bounding the area of
$D$. We begin by bounding the area of ![]() $D$ in terms of the distance between the core geodesic of
$D$ in terms of the distance between the core geodesic of ![]() $W_\alpha$ and
$W_\alpha$ and ![]() $H$.
$H$.
Lemma 5.5 Let ![]() $H$ be an isometrically immersed half-space in
$H$ be an isometrically immersed half-space in ![]() $W_\alpha$ that is disjoint from the core geodesic
$W_\alpha$ that is disjoint from the core geodesic ![]() $\alpha$ with boundary disk
$\alpha$ with boundary disk ![]() $D$. Then
$D$. Then
Proof. We can lift the picture to ![]() ${{\mathbb {H}}^3}$ and assume that
${{\mathbb {H}}^3}$ and assume that ![]() $\alpha$ has endpoints
$\alpha$ has endpoints ![]() $\pm 1$ and
$\pm 1$ and ![]() $D$ is the disk of radius
$D$ is the disk of radius ![]() $r$ centered at
$r$ centered at ![]() $0$ with
$0$ with ![]() $d(\alpha, H) = e^{-r}$. Note that while the disk
$d(\alpha, H) = e^{-r}$. Note that while the disk ![]() $D$ is embedded in
$D$ is embedded in ![]() $\mathbb {C}$ it may be immersed in
$\mathbb {C}$ it may be immersed in ![]() $\partial W_\alpha$. However, this will only decrease its area. The map
$\partial W_\alpha$. However, this will only decrease its area. The map ![]() $f(z)= (z-1)/(z+1)$ sends the geodesic
$f(z)= (z-1)/(z+1)$ sends the geodesic ![]() $\alpha$ to the geodesic with endpoints
$\alpha$ to the geodesic with endpoints ![]() $0$ and
$0$ and ![]() $\infty$. Thus, pulling back the metric
$\infty$. Thus, pulling back the metric ![]() $|dz|^2/|z|^2$, we have
$|dz|^2/|z|^2$, we have
Therefore, on ![]() $D$ we have
$D$ we have
and it follows that
In the next lemma we show that each component of ![]() $S^\alpha _\epsilon (\beta )$ lies in a round disk in
$S^\alpha _\epsilon (\beta )$ lies in a round disk in ![]() $T_\alpha = \partial W_\alpha$ which bounds a half-space in
$T_\alpha = \partial W_\alpha$ which bounds a half-space in ![]() $W_\alpha$ whose distance from the core Margulis tube
$W_\alpha$ whose distance from the core Margulis tube ![]() $T_{\epsilon _3}(\alpha )$ is given in terms of the length of the associated orthogeodesic.
$T_{\epsilon _3}(\alpha )$ is given in terms of the length of the associated orthogeodesic.
Lemma 5.6 There exists a ![]() $\delta _0 > 0$ such that if
$\delta _0 > 0$ such that if ![]() $\operatorname {Re} {\mathcal {L}}_\alpha (M_Y) <\delta _0$ and
$\operatorname {Re} {\mathcal {L}}_\alpha (M_Y) <\delta _0$ and ![]() $\epsilon < \epsilon _3/2$ then the following assertion holds. Let
$\epsilon < \epsilon _3/2$ then the following assertion holds. Let ![]() $\ell _\beta (Y) < 2\epsilon$ and
$\ell _\beta (Y) < 2\epsilon$ and ![]() ${\bf S}$ be a component of
${\bf S}$ be a component of ![]() $S^\alpha _\epsilon (\beta )$. Let
$S^\alpha _\epsilon (\beta )$. Let ![]() ${\bf T}$ be the component of
${\bf T}$ be the component of ![]() $\pi _\alpha ^{-1}(T_{2\epsilon }(\beta ))$ with
$\pi _\alpha ^{-1}(T_{2\epsilon }(\beta ))$ with ![]() $r_\alpha ({\bf S}) \subset {\bf T}$ and let
$r_\alpha ({\bf S}) \subset {\bf T}$ and let ![]() $u$ be the orthogeodesic between
$u$ be the orthogeodesic between ![]() $T_{\epsilon _3}(\alpha )$ and
$T_{\epsilon _3}(\alpha )$ and ![]() ${\bf T}$. Then there is a half-space
${\bf T}$. Then there is a half-space ![]() $H$ in
$H$ in ![]() $W_\alpha$ whose boundary disk
$W_\alpha$ whose boundary disk ![]() $D$ contains
$D$ contains ![]() ${\bf S}$ with
${\bf S}$ with
Proof. By inequality (5.2) for the radius of the Margulis tube we can choose ![]() $\delta _0 > 0$ such that if
$\delta _0 > 0$ such that if ![]() $\operatorname {Re} {\mathcal {L}}_\alpha (M_Y) <\delta _0$ then
$\operatorname {Re} {\mathcal {L}}_\alpha (M_Y) <\delta _0$ then
(choosing ![]() $\delta _0 = \epsilon _3/50$ will suffice). We also note that the inequality in the statement of the lemma follows from the lower bound on
$\delta _0 = \epsilon _3/50$ will suffice). We also note that the inequality in the statement of the lemma follows from the lower bound on ![]() $R_{\epsilon _3}(\alpha )$.
$R_{\epsilon _3}(\alpha )$.
As we assume ![]() $\ell _\beta (Y) < 2\epsilon$, it follows that
$\ell _\beta (Y) < 2\epsilon$, it follows that ![]() $S^\alpha _\epsilon (\beta )$ is non-empty so we can consider a component
$S^\alpha _\epsilon (\beta )$ is non-empty so we can consider a component ![]() ${\bf S}$. We again lift the picture to
${\bf S}$. We again lift the picture to ![]() ${{\mathbb {H}}^3}$. Let
${{\mathbb {H}}^3}$. Let ![]() $\tilde {\bf T}$ be a lift of
$\tilde {\bf T}$ be a lift of ![]() ${\bf T}$ to
${\bf T}$ to ![]() ${{\mathbb {H}}^3}$ and let
${{\mathbb {H}}^3}$ and let ![]() $\tilde u$ be a lift of
$\tilde u$ be a lift of ![]() $u$ that is orthogonal to
$u$ that is orthogonal to ![]() $\partial \tilde {\bf T}$. Further, we extend
$\partial \tilde {\bf T}$. Further, we extend ![]() $u$ to the perpendicular
$u$ to the perpendicular ![]() $v$ from
$v$ from ![]() $\partial {\bf T}$ to
$\partial {\bf T}$ to ![]() $\alpha$ with lift
$\alpha$ with lift ![]() $\tilde v$ containing
$\tilde v$ containing ![]() $\tilde u$. We can assume that
$\tilde u$. We can assume that ![]() $\tilde u$ is the vertical geodesic segment
$\tilde u$ is the vertical geodesic segment ![]() $\{0\} \times [1, e^{\ell (u)}]$ in the upper-half-space model
$\{0\} \times [1, e^{\ell (u)}]$ in the upper-half-space model ![]() ${{\mathbb {H}}^3} = \mathbb {C} \times \mathbb {R}_+$ and that
${{\mathbb {H}}^3} = \mathbb {C} \times \mathbb {R}_+$ and that ![]() $\tilde {\bf T}$ is orthogonal to
$\tilde {\bf T}$ is orthogonal to ![]() $\tilde u$ at
$\tilde u$ at ![]() $(0, 1)$. Therefore,
$(0, 1)$. Therefore, ![]() $\tilde v$ is the geodesic
$\tilde v$ is the geodesic ![]() $\{0\}\times [1,e^{\ell (v)}]$ where
$\{0\}\times [1,e^{\ell (v)}]$ where ![]() $\ell (v) = R_{\epsilon _3}(\alpha ) +\ell (u)$. Let
$\ell (v) = R_{\epsilon _3}(\alpha ) +\ell (u)$. Let ![]() $H'$ be the half-space in
$H'$ be the half-space in ![]() ${{\mathbb {H}}^3}$ that contains
${{\mathbb {H}}^3}$ that contains ![]() $\tilde {\bf T}$ and whose boundary plane is orthogonal to
$\tilde {\bf T}$ and whose boundary plane is orthogonal to ![]() $\tilde u$ at
$\tilde u$ at ![]() $(0,1) \in {{\mathbb {H}}^3}$.
$(0,1) \in {{\mathbb {H}}^3}$.
The retraction ![]() $r_\alpha$ lifts to a retraction
$r_\alpha$ lifts to a retraction
where ![]() $\Lambda$ is the limit set of the Kleinian group uniformizing
$\Lambda$ is the limit set of the Kleinian group uniformizing ![]() $M_Y$. Let
$M_Y$. Let ![]() $\tilde {\bf S}$ be the lift of
$\tilde {\bf S}$ be the lift of ![]() ${\bf S}$ with
${\bf S}$ with ![]() $\tilde r(\tilde {\bf S}) \subset \tilde {\bf T}$. Let
$\tilde r(\tilde {\bf S}) \subset \tilde {\bf T}$. Let ![]() $\tilde D \subset \mathbb {C}$ be the Euclidean disk of radius
$\tilde D \subset \mathbb {C}$ be the Euclidean disk of radius ![]() $1+ \sqrt 2$ centered at
$1+ \sqrt 2$ centered at ![]() $0 \in \mathbb {C}$ and
$0 \in \mathbb {C}$ and ![]() $\tilde H$ the half-space in
$\tilde H$ the half-space in ![]() ${{\mathbb {H}}^3}$ with boundary
${{\mathbb {H}}^3}$ with boundary ![]() $\tilde D$. We will show that
$\tilde D$. We will show that ![]() $\tilde {\bf S}\subset \tilde D$, so that if
$\tilde {\bf S}\subset \tilde D$, so that if ![]() $D$ is the image of
$D$ is the image of ![]() $\tilde D$ in
$\tilde D$ in ![]() $\partial W_\alpha$ then
$\partial W_\alpha$ then ![]() ${\bf S}\subset D$. The immersed half-space
${\bf S}\subset D$. The immersed half-space ![]() $H \subset W_\alpha$ bounded by
$H \subset W_\alpha$ bounded by ![]() $D$ is the image of
$D$ is the image of ![]() $\tilde H$ so we have that
$\tilde H$ so we have that ![]() $d(\alpha, H)$ is equal to
$d(\alpha, H)$ is equal to ![]() $\ell (v)$ minus the distance from the boundary plane of
$\ell (v)$ minus the distance from the boundary plane of ![]() $\tilde H$ to
$\tilde H$ to ![]() $H'$. As this latter distance is
$H'$. As this latter distance is ![]() $\log (1+\sqrt 2)$ this will give
$\log (1+\sqrt 2)$ this will give
If we can show the inclusion ![]() $\tilde {\bf S} \subset \tilde D$ we are done.
$\tilde {\bf S} \subset \tilde D$ we are done.
We now prove this inclusion. For ![]() $z\in \widehat {{\mathbb {C}}}\smallsetminus \Lambda$ there is a unique horosphere
$z\in \widehat {{\mathbb {C}}}\smallsetminus \Lambda$ there is a unique horosphere ![]() $\mathfrak H_z$ that intersects
$\mathfrak H_z$ that intersects ![]() $C(\Lambda )$ in a single point. This point of intersection is
$C(\Lambda )$ in a single point. This point of intersection is ![]() $\tilde r(z)$. If
$\tilde r(z)$. If ![]() $\tilde r(z) \in \tilde {\bf T}$ then
$\tilde r(z) \in \tilde {\bf T}$ then ![]() $\mathfrak H_z$ will intersect
$\mathfrak H_z$ will intersect ![]() $H'$. The perpendicular
$H'$. The perpendicular ![]() $\tilde v$ from
$\tilde v$ from ![]() $\tilde \alpha$ to
$\tilde \alpha$ to ![]() $\tilde {\bf T}$ is contained in
$\tilde {\bf T}$ is contained in ![]() $C(\Lambda )$ and therefore must not intersect the interior of
$C(\Lambda )$ and therefore must not intersect the interior of ![]() $\mathfrak H_z$. As
$\mathfrak H_z$. As ![]() $\tilde v$ is the vertical geodesic
$\tilde v$ is the vertical geodesic ![]() $\{0\}\times [1,e^{\ell (v)}]$ a simple calculation shows that when
$\{0\}\times [1,e^{\ell (v)}]$ a simple calculation shows that when ![]() $\ell (v) \geq \log (1+\sqrt {2})$ the interior of
$\ell (v) \geq \log (1+\sqrt {2})$ the interior of ![]() $\mathfrak H_z$ will intersect
$\mathfrak H_z$ will intersect ![]() $\tilde v$ if
$\tilde v$ if ![]() $|z|> 1+\sqrt 2$ (see Figure 4). By our choice of
$|z|> 1+\sqrt 2$ (see Figure 4). By our choice of ![]() $\delta _0$, we have
$\delta _0$, we have ![]() $\ell (v) = R_{\epsilon _3}(\alpha )+\ell (u) \geq \log (1+\sqrt {2})$. Therefore, if
$\ell (v) = R_{\epsilon _3}(\alpha )+\ell (u) \geq \log (1+\sqrt {2})$. Therefore, if ![]() $z\in \tilde {\bf S}$ we have that
$z\in \tilde {\bf S}$ we have that ![]() $z\in \tilde D$ and
$z\in \tilde D$ and ![]() $\tilde {\bf S} \subset \tilde D$, completing the proof.
$\tilde {\bf S} \subset \tilde D$, completing the proof.

Figure 4. Tubes, half-spaces, and horoballs.
Let ![]() ${\mathcal {O}}_\epsilon ^\alpha (\beta )$ be the set orthogeodesics from
${\mathcal {O}}_\epsilon ^\alpha (\beta )$ be the set orthogeodesics from ![]() $T_{\epsilon _3}(\alpha )$ to the components of
$T_{\epsilon _3}(\alpha )$ to the components of ![]() $\pi _\alpha ^{-1}(T_{\epsilon }(\beta ))$. With
$\pi _\alpha ^{-1}(T_{\epsilon }(\beta ))$. With ![]() $\delta _0$ as in Lemma 5.6, we have the following corollary.
$\delta _0$ as in Lemma 5.6, we have the following corollary.
Corollary 5.7 Given ![]() $\delta, \eta >0$, there exists
$\delta, \eta >0$, there exists ![]() $\epsilon >0$ such that if
$\epsilon >0$ such that if ![]() $\operatorname {Re}{\mathcal {L}}_\alpha (M_Y) < \delta _0$ and
$\operatorname {Re}{\mathcal {L}}_\alpha (M_Y) < \delta _0$ and ![]() $\operatorname {Re}{\mathcal {L}}_\beta (M_Y) < 2\delta$ then
$\operatorname {Re}{\mathcal {L}}_\beta (M_Y) < 2\delta$ then
Proof. We first show that, for ![]() $\epsilon < \epsilon _3/2$ and
$\epsilon < \epsilon _3/2$ and ![]() $\ell _\beta (Y) \leq 2\epsilon$,
$\ell _\beta (Y) \leq 2\epsilon$,
where ![]() $A$ is a universal constant.
$A$ is a universal constant.
As ![]() $\ell _\beta (Y) \leq 2\epsilon$, we have that
$\ell _\beta (Y) \leq 2\epsilon$, we have that ![]() $S^\alpha _\epsilon (\beta )$ is non-empty. Given a component
$S^\alpha _\epsilon (\beta )$ is non-empty. Given a component ![]() ${\bf S}$ of
${\bf S}$ of ![]() $S^\alpha _\epsilon (\beta )$, let
$S^\alpha _\epsilon (\beta )$, let ![]() ${\bf T}$ be the component of
${\bf T}$ be the component of ![]() $\pi _\alpha ^{-1}(T_{2\epsilon }(\beta ))$ with
$\pi _\alpha ^{-1}(T_{2\epsilon }(\beta ))$ with ![]() $r_\alpha ({\bf S}) \subset {\bf T}$ and let
$r_\alpha ({\bf S}) \subset {\bf T}$ and let ![]() $u$ be the orthogeodesic between
$u$ be the orthogeodesic between ![]() $T_{\epsilon _3}(\alpha )$ and
$T_{\epsilon _3}(\alpha )$ and ![]() ${\bf T}$. Then as
${\bf T}$. Then as ![]() $\operatorname {Re}{\mathcal {L}}_\alpha (M_Y) < \delta _0$, by Lemma 5.6, there is an immersed half-space
$\operatorname {Re}{\mathcal {L}}_\alpha (M_Y) < \delta _0$, by Lemma 5.6, there is an immersed half-space ![]() $H$ in
$H$ in ![]() $W_\alpha$ whose boundary disk
$W_\alpha$ whose boundary disk ![]() $D$ contains
$D$ contains ![]() ${\bf S}$ with
${\bf S}$ with
If ![]() $t\ge \log \sqrt 2$ then
$t\ge \log \sqrt 2$ then ![]() $\sinh (t) \ge e^t/4$. Since the disk
$\sinh (t) \ge e^t/4$. Since the disk ![]() $D$ contains
$D$ contains ![]() ${\bf S}$ and by Lemma 5.6 we have
${\bf S}$ and by Lemma 5.6 we have ![]() $d(\alpha, H) \ge \sqrt {2}$, we can combine this estimate on
$d(\alpha, H) \ge \sqrt {2}$, we can combine this estimate on ![]() $\sinh$ with Lemma 5.5 to get
$\sinh$ with Lemma 5.5 to get
By (5.2) we have
Together the two estimates give
Summing over the set of all orthogeodesics in ![]() ${\mathcal {O}}^\alpha _{2\epsilon }(\beta )$ gives our first estimate.
${\mathcal {O}}^\alpha _{2\epsilon }(\beta )$ gives our first estimate.
Now let ![]() $2\epsilon < \delta$. We let
$2\epsilon < \delta$. We let ![]() ${\bf T}'$ be the component of
${\bf T}'$ be the component of ![]() $\pi ^{-1}_\alpha \big (T_{\delta }(\beta )\big )$ that contains
$\pi ^{-1}_\alpha \big (T_{\delta }(\beta )\big )$ that contains ![]() ${\bf T}$ and let
${\bf T}$ and let ![]() $u'$ be the orthogeodesic between
$u'$ be the orthogeodesic between ![]() $T_{\epsilon _3}(\alpha )$ and
$T_{\epsilon _3}(\alpha )$ and ![]() ${\bf T}'$. Note that the map
${\bf T}'$. Note that the map ![]() $u\mapsto u'$ defines an bijection between
$u\mapsto u'$ defines an bijection between ![]() ${\mathcal {O}}^\alpha _{2\epsilon }(\beta )$ and
${\mathcal {O}}^\alpha _{2\epsilon }(\beta )$ and ![]() ${\mathcal {O}}^\alpha _{\delta }(\beta )$. Then
${\mathcal {O}}^\alpha _{\delta }(\beta )$. Then ![]() $u'$ is a subsegment of
$u'$ is a subsegment of ![]() $u$ and
$u$ and
where the function on the right comes from Theorem 5.4. Thus, for ![]() $\ell _\beta (Y) \leq 2\epsilon$,
$\ell _\beta (Y) \leq 2\epsilon$,
For ![]() $\ell _\beta (Y) > 2\epsilon$ the inequality also holds trivially as
$\ell _\beta (Y) > 2\epsilon$ the inequality also holds trivially as ![]() $S^\alpha _\epsilon (\beta ) = \emptyset$ and as
$S^\alpha _\epsilon (\beta ) = \emptyset$ and as ![]() $\operatorname {Re}{\mathcal {L}}_\beta (M_Y) <2\delta$, the right-hand side is positive. Thus, as
$\operatorname {Re}{\mathcal {L}}_\beta (M_Y) <2\delta$, the right-hand side is positive. Thus, as ![]() $d^l_{\delta }(2\epsilon )\to \infty$ as
$d^l_{\delta }(2\epsilon )\to \infty$ as ![]() $\epsilon \to 0$ the theorem follows.
$\epsilon \to 0$ the theorem follows.
5.3 Uniform bounds on the Poincaré series
Except for the last lemma, in this subsection ![]() $M= {{\mathbb {H}}^3}/\Gamma$ can be any complete hyperbolic
$M= {{\mathbb {H}}^3}/\Gamma$ can be any complete hyperbolic ![]() $3$-manifold uniformized by a Kleinian group
$3$-manifold uniformized by a Kleinian group ![]() $\Gamma$.
$\Gamma$.
For ![]() $x\in {{\mathbb {H}}^3}$ we define the Poincaré series
$x\in {{\mathbb {H}}^3}$ we define the Poincaré series
where ![]() $d$ is the hyperbolic distance. Poincaré series play an important role in dynamics, but here we will only be interested in obtaining uniform bounds on
$d$ is the hyperbolic distance. Poincaré series play an important role in dynamics, but here we will only be interested in obtaining uniform bounds on ![]() $P_\alpha (x)$ which we will then use to bound the similar exponential sum of lengths of orthogeodesics that appears in Corollary 5.7.
$P_\alpha (x)$ which we will then use to bound the similar exponential sum of lengths of orthogeodesics that appears in Corollary 5.7.
We have the following elementary bound.
Lemma 5.8
– Let
 ${\mathcal {C}}$ be a closed convex set in
${\mathcal {C}}$ be a closed convex set in  ${{\mathbb {H}}^3}$ and
${{\mathbb {H}}^3}$ and  $\bar {\mathcal {C}}$ be closure in
$\bar {\mathcal {C}}$ be closure in  ${\bar {\mathbb {H}}^3} ={{\mathbb {H}}^3} \cup \widehat {{\mathbb {C}}}$. Let
be the nearest point projection. If
${\bar {\mathbb {H}}^3} ={{\mathbb {H}}^3} \cup \widehat {{\mathbb {C}}}$. Let
be the nearest point projection. If \[ r\colon {\bar{\mathbb{H}}^3}\to \bar{\mathcal{C}} \]
\[ r\colon {\bar{\mathbb{H}}^3}\to \bar{\mathcal{C}} \]
 $x \in \partial {\mathcal {C}}$ and
$x \in \partial {\mathcal {C}}$ and  $B_x(\epsilon )$ is the
$B_x(\epsilon )$ is the  $\epsilon$ ball centered at
$\epsilon$ ball centered at  $x$ then
$x$ then  $r^{-1}(B_x(\epsilon ))$ contains a round disk
$r^{-1}(B_x(\epsilon ))$ contains a round disk  $D \subset \widehat {{\mathbb {C}}}$ that bounds a half-space
$D \subset \widehat {{\mathbb {C}}}$ that bounds a half-space  $H\subset {{\mathbb {H}}^3}$ with
$H\subset {{\mathbb {H}}^3}$ with
 \[ e^{d(x,H)} \le 2\coth(\epsilon). \]
\[ e^{d(x,H)} \le 2\coth(\epsilon). \]
– Given
 $x \in {{\mathbb {H}}^3}$ and a half-space
$x \in {{\mathbb {H}}^3}$ and a half-space  $H\subset {{\mathbb {H}}^3}$ with boundary disk
$H\subset {{\mathbb {H}}^3}$ with boundary disk  $D \subset \widehat {{\mathbb {C}}}$, we have
where
$D \subset \widehat {{\mathbb {C}}}$, we have
where \[ {\operatorname{{\bf area}}}_x(D) \ge \pi e^{-2d(x,H)}, \]
\[ {\operatorname{{\bf area}}}_x(D) \ge \pi e^{-2d(x,H)}, \]
 ${\operatorname {{\bf area}}}_x$ is the visual measure on
${\operatorname {{\bf area}}}_x$ is the visual measure on  $\widehat {{\mathbb {C}}}$ determined by
$\widehat {{\mathbb {C}}}$ determined by  $x$.
$x$.
Proof. Let ![]() $P$ be a support plane for
$P$ be a support plane for ![]() ${\mathcal {C}}$ at
${\mathcal {C}}$ at ![]() $x$. Then
$x$. Then ![]() $P$ bounds a half-space whose interior is disjoint from the interior of
$P$ bounds a half-space whose interior is disjoint from the interior of ![]() ${\mathcal {C}}$, and we let
${\mathcal {C}}$, and we let ![]() $D$ be the round disk in the conformal boundary of this half-space that projects orthogonally to
$D$ be the round disk in the conformal boundary of this half-space that projects orthogonally to ![]() $P$ with image in
$P$ with image in ![]() $P \cap B_x(\epsilon )$. Let
$P \cap B_x(\epsilon )$. Let ![]() $y$ be the point on
$y$ be the point on ![]() $H$ closest to
$H$ closest to ![]() $x$,
$x$, ![]() $z$ a point in
$z$ a point in ![]() $\partial D$, and
$\partial D$, and ![]() $w$ the orthogonal projection of
$w$ the orthogonal projection of ![]() $z$ to
$z$ to ![]() $P$. Then
$P$. Then ![]() $wxyz$ forms a planar quadrilateral with one ideal vertex at
$wxyz$ forms a planar quadrilateral with one ideal vertex at ![]() $z$ and right angles at all other vertices. Standard formulas give
$z$ and right angles at all other vertices. Standard formulas give ![]() $\sinh d(x,y) \sinh d(x,w) = 1$, which can be rewritten in a less symmetric form as
$\sinh d(x,y) \sinh d(x,w) = 1$, which can be rewritten in a less symmetric form as ![]() $\cosh d(x,y) = \coth d(x,w)$. Noting that
$\cosh d(x,y) = \coth d(x,w)$. Noting that ![]() $d(x,y) = d(x,H)$,
$d(x,y) = d(x,H)$, ![]() $d(x,w) = \epsilon$, and
$d(x,w) = \epsilon$, and ![]() $e^t \le 2\cosh t$, we have
$e^t \le 2\cosh t$, we have ![]() $e^{d(x,H)} \le 2 \coth (\epsilon )$, so we will be done if we can show that
$e^{d(x,H)} \le 2 \coth (\epsilon )$, so we will be done if we can show that ![]() $r(D) \subset B_x(\epsilon )$.
$r(D) \subset B_x(\epsilon )$.
For ![]() $z \in D$ let
$z \in D$ let ![]() $\gamma$ be the geodesic in
$\gamma$ be the geodesic in ![]() ${\bar {\mathbb {H}}^3}$ from
${\bar {\mathbb {H}}^3}$ from ![]() $z$ to
$z$ to ![]() $r(z)$ and let
$r(z)$ and let ![]() $p = P \cap \gamma$. Note that
$p = P \cap \gamma$. Note that ![]() $r(z) = r(p)$, and since
$r(z) = r(p)$, and since ![]() $r$ is a contraction (and
$r$ is a contraction (and ![]() $r(x) = x$) we have that
$r(x) = x$) we have that ![]() $d(x, r(z)) \le d(x, p)$. Let
$d(x, r(z)) \le d(x, p)$. Let ![]() $B'$ be the ball of radius
$B'$ be the ball of radius ![]() $d(x,p)$ centered at
$d(x,p)$ centered at ![]() $x$ and let
$x$ and let ![]() $H_p$ be the closed half-space whose boundary is tangent to
$H_p$ be the closed half-space whose boundary is tangent to ![]() $B'$ at
$B'$ at ![]() $p$ and whose interior is disjoint from
$p$ and whose interior is disjoint from ![]() $x$ (see Figure 5). If
$x$ (see Figure 5). If ![]() $r(z) \neq p$ then
$r(z) \neq p$ then ![]() $r(z)$ is in the interior of
$r(z)$ is in the interior of ![]() $B'$ and is hence disjoint from
$B'$ and is hence disjoint from ![]() $H_p$. As
$H_p$. As ![]() $\gamma$ intersects the boundary plane of
$\gamma$ intersects the boundary plane of ![]() $H_p$ we have that
$H_p$ we have that ![]() $z$, the other endpoint of
$z$, the other endpoint of ![]() $\gamma$, will be contained in
$\gamma$, will be contained in ![]() $H_p$. As the boundary plane of
$H_p$. As the boundary plane of ![]() $H_p$ is orthogonal to
$H_p$ is orthogonal to ![]() $P$, the orthogonal projection of every point in
$P$, the orthogonal projection of every point in ![]() $H_p$ to
$H_p$ to ![]() $P$ will have distance from
$P$ will have distance from ![]() $x$ that is at least
$x$ that is at least ![]() $d(x,p)$, so we have
$d(x,p)$, so we have ![]() $d(x,p) < \epsilon$. Combining inequalities gives
$d(x,p) < \epsilon$. Combining inequalities gives ![]() $d(x, r(z)) \le \epsilon$ when
$d(x, r(z)) \le \epsilon$ when ![]() $r(z) \neq p$. If
$r(z) \neq p$. If ![]() $r(z) = p$ then the interior of
$r(z) = p$ then the interior of ![]() $\gamma$ will be disjoint from
$\gamma$ will be disjoint from ![]() $B'$ as for every
$B'$ as for every ![]() $q \in \gamma$ we have
$q \in \gamma$ we have ![]() $r(q) = r(z) = p$ and
$r(q) = r(z) = p$ and ![]() $d(q,x) \ge d(p,x)$ by the contraction of
$d(q,x) \ge d(p,x)$ by the contraction of ![]() $r$. However, if
$r$. However, if ![]() $\gamma$ is not contained in
$\gamma$ is not contained in ![]() $H_p$ it must intersect the interior of
$H_p$ it must intersect the interior of ![]() $B'$. Therefore,
$B'$. Therefore, ![]() $\gamma$, and in particular
$\gamma$, and in particular ![]() $z$, lie in
$z$, lie in ![]() $H_p$. As above, this implies that
$H_p$. As above, this implies that ![]() $r(z) \in B_x(\epsilon )$, completing the proof that
$r(z) \in B_x(\epsilon )$, completing the proof that ![]() $r(D) \subset B_x(\epsilon )$.
$r(D) \subset B_x(\epsilon )$.

Figure 5. View in the Klein model.
For the second part of the lemma, as above let ![]() $y$ be the point on
$y$ be the point on ![]() $H$ closest to
$H$ closest to ![]() $x$ and let
$x$ and let ![]() $z$ be a point in
$z$ be a point in ![]() $\partial D$. These three points from a right triangle with one ideal angle at
$\partial D$. These three points from a right triangle with one ideal angle at ![]() $z$ and angle
$z$ and angle ![]() $\theta$ at
$\theta$ at ![]() $x$. Therefore,
$x$. Therefore, ![]() $D$ is a spherical disk of radius
$D$ is a spherical disk of radius ![]() $\theta$ in the visual metric based at
$\theta$ in the visual metric based at ![]() $x$. For such right triangles we have
$x$. For such right triangles we have ![]() $\operatorname {sech} d(x,y) = \sin \theta$. The area of a spherical triangle is
$\operatorname {sech} d(x,y) = \sin \theta$. The area of a spherical triangle is ![]() $2\pi (1-\cos \theta )$, so
$2\pi (1-\cos \theta )$, so ![]() $\sin ^2\theta = 1-\cos ^2\theta \le {\operatorname {{\bf area}}}_x(D)/\pi$. Since
$\sin ^2\theta = 1-\cos ^2\theta \le {\operatorname {{\bf area}}}_x(D)/\pi$. Since ![]() $e^{-2d(x,y)} \le \operatorname {sech} d(x,y)$ and
$e^{-2d(x,y)} \le \operatorname {sech} d(x,y)$ and ![]() $d(x,y) = d(x,H)$, we can combine expressions to get
$d(x,y) = d(x,H)$, we can combine expressions to get
Using these estimates, we can obtain our uniform bound on the Poincaré series.
Lemma 5.9 If ![]() $M ={{\mathbb {H}}^3}/\Gamma$ is a hyperbolic
$M ={{\mathbb {H}}^3}/\Gamma$ is a hyperbolic ![]() $3$-manifold and
$3$-manifold and ![]() $x$ a point on the boundary of the convex core
$x$ a point on the boundary of the convex core ![]() $C(M)$ with injectivity radius
$C(M)$ with injectivity radius ![]() $\geq \epsilon$, then for
$\geq \epsilon$, then for ![]() $\tilde x$ a lift of
$\tilde x$ a lift of ![]() $x$ to
$x$ to ![]() ${{\mathbb {H}}^3}$ we have
${{\mathbb {H}}^3}$ we have
Proof. Let ![]() $\Lambda$ be the limit set of
$\Lambda$ be the limit set of ![]() $\Gamma$ and
$\Gamma$ and ![]() $r:{\bar {\mathbb {H}}^3} \rightarrow C(\Lambda )$ be the retract map to the convex hull of the limit set. Let
$r:{\bar {\mathbb {H}}^3} \rightarrow C(\Lambda )$ be the retract map to the convex hull of the limit set. Let ![]() $B_\epsilon (\tilde x)$ be the ball of radius
$B_\epsilon (\tilde x)$ be the ball of radius ![]() $\epsilon$ about
$\epsilon$ about ![]() $\tilde x$. As the injectivity radius of
$\tilde x$. As the injectivity radius of ![]() $x$ is
$x$ is ![]() $\ge \epsilon$ we have
$\ge \epsilon$ we have ![]() $B_\epsilon \cap \gamma (B_\epsilon ) = \emptyset$ for all
$B_\epsilon \cap \gamma (B_\epsilon ) = \emptyset$ for all ![]() $\gamma \in \Gamma \smallsetminus \{\operatorname {id}\}$. We define
$\gamma \in \Gamma \smallsetminus \{\operatorname {id}\}$. We define ![]() $U = r^{-1}(B_\epsilon )\cap \widehat {{\mathbb {C}}}$. Since
$U = r^{-1}(B_\epsilon )\cap \widehat {{\mathbb {C}}}$. Since ![]() $r$ is
$r$ is ![]() $\Gamma$-invariant we have
$\Gamma$-invariant we have ![]() $U \cap \gamma (U) = r^{-1}(B_\epsilon \cap \gamma (B_\epsilon ))= \emptyset$ if
$U \cap \gamma (U) = r^{-1}(B_\epsilon \cap \gamma (B_\epsilon ))= \emptyset$ if ![]() $\gamma \in \Gamma \smallsetminus \{\operatorname {id}\}$. By Lemma 5.8 we have that
$\gamma \in \Gamma \smallsetminus \{\operatorname {id}\}$. By Lemma 5.8 we have that ![]() $U$ contains a disk
$U$ contains a disk ![]() $D$ that bounds a half-space
$D$ that bounds a half-space ![]() $H$ with
$H$ with ![]() $e^{d(\tilde x, H)} \le 2 \coth (\epsilon )$. By the triangle inequality for all
$e^{d(\tilde x, H)} \le 2 \coth (\epsilon )$. By the triangle inequality for all ![]() $\gamma \in \Gamma$ we have that
$\gamma \in \Gamma$ we have that ![]() $d(\tilde x,\gamma (H)) \le d(\tilde x, \gamma (\tilde x)) +d(\gamma (\tilde x), \gamma (H))$. As
$d(\tilde x,\gamma (H)) \le d(\tilde x, \gamma (\tilde x)) +d(\gamma (\tilde x), \gamma (H))$. As ![]() $d(\gamma (\tilde x), \gamma (H)) = d(\tilde x, H)$ this gives
$d(\gamma (\tilde x), \gamma (H)) = d(\tilde x, H)$ this gives ![]() $d(\tilde x, \gamma (\tilde x)) \ge d(\tilde x, \gamma (H)) - d(\tilde x, H)$ which in turn implies
$d(\tilde x, \gamma (\tilde x)) \ge d(\tilde x, \gamma (H)) - d(\tilde x, H)$ which in turn implies
 \begin{align*} \sum_{\gamma\in \Gamma} e^{-2d(\tilde x, \gamma(\tilde x))} & \le e^{2d(\tilde x, H)} \sum_{\gamma} e^{-2d(\tilde x, \gamma(H))}\\ & \le 2\pi^{-1}\coth^2(\epsilon) \sum_{\gamma\in \Gamma} {\operatorname{{\bf area}}}_{\tilde x}(\gamma(D))\\ &\le 8\coth^2(\epsilon), \end{align*}
\begin{align*} \sum_{\gamma\in \Gamma} e^{-2d(\tilde x, \gamma(\tilde x))} & \le e^{2d(\tilde x, H)} \sum_{\gamma} e^{-2d(\tilde x, \gamma(H))}\\ & \le 2\pi^{-1}\coth^2(\epsilon) \sum_{\gamma\in \Gamma} {\operatorname{{\bf area}}}_{\tilde x}(\gamma(D))\\ &\le 8\coth^2(\epsilon), \end{align*}
where the last sum is bounded by ![]() ${\operatorname {{\bf area}}}_{\tilde x}(\widehat {{\mathbb {C}}}) = 4\pi$ since the disks
${\operatorname {{\bf area}}}_{\tilde x}(\widehat {{\mathbb {C}}}) = 4\pi$ since the disks ![]() $\gamma (D)$ are all disjoint.
$\gamma (D)$ are all disjoint.
We can now obtain a uniform bound on the exponential sum of orthogeodesic lengths.
Lemma 5.10 Fix ![]() $\delta <\epsilon _3$ and assume that
$\delta <\epsilon _3$ and assume that ![]() $\alpha$ and
$\alpha$ and ![]() $\beta$ are closed geodesics in
$\beta$ are closed geodesics in ![]() $M_Y \in CC(N,S;X)$ with length
$M_Y \in CC(N,S;X)$ with length ![]() $\le 2\delta$. Then the sum
$\le 2\delta$. Then the sum
is bounded by a constant that only depends on ![]() $\delta$ and the diameter of
$\delta$ and the diameter of ![]() $C(M_Y)^{>\delta }$.
$C(M_Y)^{>\delta }$.
Proof. Choose ![]() $x \in \partial C(M_Y) \cap C(M_Y)^{\ge \epsilon _3}$ and let
$x \in \partial C(M_Y) \cap C(M_Y)^{\ge \epsilon _3}$ and let ![]() $\tilde x \in {{\mathbb {H}}^3}$ be in the pre-image of
$\tilde x \in {{\mathbb {H}}^3}$ be in the pre-image of ![]() $x$ under the covering map
$x$ under the covering map ![]() ${{\mathbb {H}}^3} \to M_Y$. We will define a map
${{\mathbb {H}}^3} \to M_Y$. We will define a map ![]() $\psi$ from
$\psi$ from ![]() ${\mathcal {O}}^\alpha _\delta (\beta )$ to
${\mathcal {O}}^\alpha _\delta (\beta )$ to ![]() $\Gamma$ such that
$\Gamma$ such that ![]() $\ell (u) \ge d(\tilde x, \psi (u)(\tilde x)) - 2D$, where
$\ell (u) \ge d(\tilde x, \psi (u)(\tilde x)) - 2D$, where ![]() $D$ is the diameter of
$D$ is the diameter of ![]() $C(M_Y)^{>\delta }$ and
$C(M_Y)^{>\delta }$ and ![]() $\psi$ is at most
$\psi$ is at most ![]() $N$-to-one. Once we have defined such a
$N$-to-one. Once we have defined such a ![]() $\psi$ we have that
$\psi$ we have that
We claim that there exists an integer ![]() $N_0$ such that at most
$N_0$ such that at most ![]() $N_0$ components of the pre-image of
$N_0$ components of the pre-image of ![]() $T_{\epsilon _3}(\alpha )$ and
$T_{\epsilon _3}(\alpha )$ and ![]() $T_{\epsilon _3}(\beta )$ in
$T_{\epsilon _3}(\beta )$ in ![]() ${{\mathbb {H}}^3}$ intersect any ball of radius
${{\mathbb {H}}^3}$ intersect any ball of radius ![]() $D$. To see this we note that as
$D$. To see this we note that as ![]() $\beta$ has length less than
$\beta$ has length less than ![]() $2\delta$,
$2\delta$, ![]() $T_{\delta }(\beta )$ is non-empty. Thus, each point in
$T_{\delta }(\beta )$ is non-empty. Thus, each point in ![]() $T_{\epsilon _3}(\beta )$ is contained in a ball of radius
$T_{\epsilon _3}(\beta )$ is contained in a ball of radius ![]() $r = d^l_{\epsilon _3}(\delta )$ which lies inside
$r = d^l_{\epsilon _3}(\delta )$ which lies inside ![]() $T_{\epsilon _3}(\beta )$. Therefore, there are
$T_{\epsilon _3}(\beta )$. Therefore, there are ![]() $N_0$ disjoint balls of radius
$N_0$ disjoint balls of radius ![]() $r$ in the ball of radius
$r$ in the ball of radius ![]() $D+2r$. Thus,
$D+2r$. Thus, ![]() $N_0\operatorname {vol}(B_r) \leq \operatorname {vol}(B_{D+2r})$ bounding
$N_0\operatorname {vol}(B_r) \leq \operatorname {vol}(B_{D+2r})$ bounding ![]() $N_0$. Let
$N_0$. Let ![]() $N = N_0^2$.
$N = N_0^2$.
For each ![]() $u \in {\mathcal {O}}^\alpha _\delta (\beta )$ we will carefully choose a lift
$u \in {\mathcal {O}}^\alpha _\delta (\beta )$ we will carefully choose a lift ![]() $\tilde u$ to
$\tilde u$ to ![]() ${{\mathbb {H}}^3}$. More precisely, we will carefully choose where the initial endpoint
${{\mathbb {H}}^3}$. More precisely, we will carefully choose where the initial endpoint ![]() $\tilde u_-$ lies and then the terminal endpoint
$\tilde u_-$ lies and then the terminal endpoint ![]() $\tilde u_+$ will determine
$\tilde u_+$ will determine ![]() $\psi (u)$. Note that the endpoints
$\psi (u)$. Note that the endpoints ![]() $\tilde u_-$ and
$\tilde u_-$ and ![]() $\tilde u_+$ will lie in the pre-image of
$\tilde u_+$ will lie in the pre-image of ![]() $C(M)^{>\delta }$, so we can choose
$C(M)^{>\delta }$, so we can choose ![]() $\tilde u_-$ such that
$\tilde u_-$ such that ![]() $d(\tilde x, \tilde u_-) \le D$. Then there will be a
$d(\tilde x, \tilde u_-) \le D$. Then there will be a ![]() $\gamma \in \Gamma$ with
$\gamma \in \Gamma$ with ![]() $d(\gamma (\tilde x), \tilde u_+)\le D$ and we define
$d(\gamma (\tilde x), \tilde u_+)\le D$ and we define ![]() $\psi (u) = \gamma$. It follows that
$\psi (u) = \gamma$. It follows that
The orthogeodesic ![]() $u$ is determined by the components in the pre-image of
$u$ is determined by the components in the pre-image of ![]() $T_{\epsilon _3}(\alpha )$ and
$T_{\epsilon _3}(\alpha )$ and ![]() $T_{\epsilon _3}(\beta )$ that
$T_{\epsilon _3}(\beta )$ that ![]() $\tilde u_-$ and
$\tilde u_-$ and ![]() $\tilde u_+$ lie in. As there are at most
$\tilde u_+$ lie in. As there are at most ![]() $N_0$ in a
$N_0$ in a ![]() $D$-neighborhood of
$D$-neighborhood of ![]() $\tilde x$ and
$\tilde x$ and ![]() $N_0$ in a
$N_0$ in a ![]() $D$-neighborhood of
$D$-neighborhood of ![]() $\gamma (\tilde x)$, there are at most
$\gamma (\tilde x)$, there are at most ![]() $N = N_0^2$ orthogeodesics
$N = N_0^2$ orthogeodesics ![]() $u$ with
$u$ with ![]() $\psi (u) = N$, so
$\psi (u) = N$, so ![]() $\psi$ is at most
$\psi$ is at most ![]() $N$-to-one.
$N$-to-one.
For the previous lemma to be useful need to able to control the diameter of ![]() $C(M_Y)^{>\epsilon }$. The following argument is well known.
$C(M_Y)^{>\epsilon }$. The following argument is well known.
Lemma 5.11 Let ![]() $\epsilon > 0$ and
$\epsilon > 0$ and ![]() $V> 0$. Let
$V> 0$. Let ![]() $M$ be a geometrically finite hyperbolic manifold and convex core volume less than
$M$ be a geometrically finite hyperbolic manifold and convex core volume less than ![]() $V$. Then the diameter of every connected component of
$V$. Then the diameter of every connected component of ![]() $C(M)^{>\epsilon }$, the
$C(M)^{>\epsilon }$, the ![]() $\epsilon$-thick part of the convex core, is bounded by a constant that is a function of
$\epsilon$-thick part of the convex core, is bounded by a constant that is a function of ![]() $\epsilon$,
$\epsilon$, ![]() $V$,
$V$, ![]() $\chi (\partial M)$, and the length of the shortest compressible curve in
$\chi (\partial M)$, and the length of the shortest compressible curve in ![]() $\partial C(M)$.
$\partial C(M)$.
Proof. Given ![]() $x,y$ in the connected component of
$x,y$ in the connected component of ![]() $C(M)^{> \epsilon }$, let
$C(M)^{> \epsilon }$, let ![]() $\gamma :[0,1]\rightarrow C(M)^{> \epsilon }$ be a path joining
$\gamma :[0,1]\rightarrow C(M)^{> \epsilon }$ be a path joining ![]() $x,y$. Then
$x,y$. Then ![]() $f(t) = d(x, \gamma (t))$ is continuous with
$f(t) = d(x, \gamma (t))$ is continuous with ![]() $f(0) = 0$ and
$f(0) = 0$ and ![]() $f(1) = d(x,y)$ and we can take
$f(1) = d(x,y)$ and we can take ![]() $t_k \in [0,1]$ with
$t_k \in [0,1]$ with ![]() $f(t_k) = 2k\epsilon$ for
$f(t_k) = 2k\epsilon$ for ![]() $0\le k \leq n$ where
$0\le k \leq n$ where ![]() $2n\epsilon \leq d(x,y) < 2(n+1)\epsilon$. Then the balls
$2n\epsilon \leq d(x,y) < 2(n+1)\epsilon$. Then the balls ![]() $B(\gamma (t_k), \epsilon )$ are disjoint, embedded, and contained in
$B(\gamma (t_k), \epsilon )$ are disjoint, embedded, and contained in ![]() $N_\epsilon (C(M))$. Thus, the number of disjoint
$N_\epsilon (C(M))$. Thus, the number of disjoint ![]() $\epsilon$-balls is bounded in terms of the volume of
$\epsilon$-balls is bounded in terms of the volume of ![]() $N_\epsilon (C(M))$ which in turn bounds
$N_\epsilon (C(M))$ which in turn bounds ![]() $d(x,y)$.
$d(x,y)$.
To bound the volume of ![]() $N_\epsilon (C(M))$, let
$N_\epsilon (C(M))$, let ![]() $V_t$ be the volume of
$V_t$ be the volume of ![]() $N_t(C(M))$. Then
$N_t(C(M))$. Then ![]() $\dot V_t = A_t$ is the area of
$\dot V_t = A_t$ is the area of ![]() $\partial N_t(C(M))$. If
$\partial N_t(C(M))$. If ![]() $\beta _M$ is the bending lamination on
$\beta _M$ is the bending lamination on ![]() $\partial C(M)$ then an easy calculation gives
$\partial C(M)$ then an easy calculation gives
where ![]() $L(\beta _M)$ is the length of
$L(\beta _M)$ is the length of ![]() $\beta _M$. Also, by [Reference Bridgeman, Brock and BrombergBBB19], there are universal constants
$\beta _M$. Also, by [Reference Bridgeman, Brock and BrombergBBB19], there are universal constants ![]() $A, B$ such that
$A, B$ such that ![]() $L(\beta _M) \leq (A + B/\delta )|\chi (\partial M)|$. Integrating, it follows that the volume of
$L(\beta _M) \leq (A + B/\delta )|\chi (\partial M)|$. Integrating, it follows that the volume of ![]() $N_\epsilon (C(M))$ is bounded by a function of
$N_\epsilon (C(M))$ is bounded by a function of ![]() $V$,
$V$, ![]() $\chi (\partial M)$, and
$\chi (\partial M)$, and ![]() $\delta$.
$\delta$.
To apply the previous lemma to bound the diameter of ![]() $C(M)^{>\epsilon }$, we need to know that this set is connected. In general this will be false. The next lemma shows that in our setting it holds for sufficiently small
$C(M)^{>\epsilon }$, we need to know that this set is connected. In general this will be false. The next lemma shows that in our setting it holds for sufficiently small ![]() $\epsilon$ for hyperbolic manifolds in a relatively acylindrical deformation space.
$\epsilon$ for hyperbolic manifolds in a relatively acylindrical deformation space.
Lemma 5.12 Given ![]() $CC(N,S;X)$ with
$CC(N,S;X)$ with ![]() $(N,S)$ relatively acylindrical, there exists a
$(N,S)$ relatively acylindrical, there exists a ![]() $\delta > 0$ such that if
$\delta > 0$ such that if ![]() $M \in CC(N,S;X)$ then
$M \in CC(N,S;X)$ then ![]() $C(M)^{>\delta }$ is connected.
$C(M)^{>\delta }$ is connected.
Proof. Let ![]() $X'$ be the union of components of
$X'$ be the union of components of ![]() $\partial C(M)$ that face
$\partial C(M)$ that face ![]() $X$. The retraction from
$X$. The retraction from ![]() $X$ to
$X$ to ![]() $\partial C(M)$ is Lipschitz with Lipschitz constant only depending on
$\partial C(M)$ is Lipschitz with Lipschitz constant only depending on ![]() $\operatorname {inj}(X)$ (see [Reference Bridgeman and CanaryBC03]). Therefore, the diameter of
$\operatorname {inj}(X)$ (see [Reference Bridgeman and CanaryBC03]). Therefore, the diameter of ![]() $X$ is bounded by
$X$ is bounded by ![]() $D$, a constant depending only on
$D$, a constant depending only on ![]() $\chi (X)$ and
$\chi (X)$ and ![]() $\operatorname {inj}(X)$.
$\operatorname {inj}(X)$.
Let ![]() $Y'$ be the union of components of
$Y'$ be the union of components of ![]() $\partial C(M)$ facing
$\partial C(M)$ facing ![]() $Y$ and recall that the path metric on
$Y$ and recall that the path metric on ![]() $Y'$ is hyperbolic. Since
$Y'$ is hyperbolic. Since ![]() $(N;S)$ is relatively acylindrical there is at most one homotopy class of curve in
$(N;S)$ is relatively acylindrical there is at most one homotopy class of curve in ![]() $S$ that is homotopic to
$S$ that is homotopic to ![]() $\alpha$. If there is such a curve, let
$\alpha$. If there is such a curve, let ![]() $C$ be the
$C$ be the ![]() $\epsilon _3$-Margulis collar about its geodesic representative
$\epsilon _3$-Margulis collar about its geodesic representative ![]() $\alpha '$ in
$\alpha '$ in ![]() $Y'$. Note that if there is no such curve or the curve has length
$Y'$. Note that if there is no such curve or the curve has length ![]() $\ge 2\epsilon _3$ then
$\ge 2\epsilon _3$ then ![]() $C$ is empty. By a theorem of Bers,
$C$ is empty. By a theorem of Bers, ![]() $Y'$ has a bounded length pants decomposition with constants only depending on the topology of
$Y'$ has a bounded length pants decomposition with constants only depending on the topology of ![]() $Y'$, and each point in the
$Y'$, and each point in the ![]() $\epsilon _3$-thick part of
$\epsilon _3$-thick part of ![]() $Y'$ is a uniformly bounded distance from at least two of these curves. On the other hand, if
$Y'$ is a uniformly bounded distance from at least two of these curves. On the other hand, if ![]() $p$ is in the
$p$ is in the ![]() $\epsilon _3$-thin part but not in
$\epsilon _3$-thin part but not in ![]() $C$ there is an essential curve of length
$C$ there is an essential curve of length ![]() $\le 2\epsilon _3$ that is not homotopic to a multiple of
$\le 2\epsilon _3$ that is not homotopic to a multiple of ![]() $\alpha$. Therefore, there exists an
$\alpha$. Therefore, there exists an ![]() $L > 0$ such that, for
$L > 0$ such that, for ![]() $p \in Y'-C$, there is a closed curve of length
$p \in Y'-C$, there is a closed curve of length ![]() $\leq L$ containing
$\leq L$ containing ![]() $p$ which is not homotopic to a multiple of
$p$ which is not homotopic to a multiple of ![]() $\alpha$.
$\alpha$.
We now choose ![]() $\delta > 0$ such that
$\delta > 0$ such that ![]() $d^l_{\epsilon _3}(\delta ) \geq \max \{D,L\}$. Let
$d^l_{\epsilon _3}(\delta ) \geq \max \{D,L\}$. Let ![]() $p$ be a point in
$p$ be a point in ![]() $\partial C(M) \cap T_\delta (\alpha )$. If
$\partial C(M) \cap T_\delta (\alpha )$. If ![]() $p \in X'$ then the diameter bound on
$p \in X'$ then the diameter bound on ![]() $X'$ implies that
$X'$ implies that ![]() $X' \subset T_{\epsilon _3}(\alpha )$. This is a contradiction since
$X' \subset T_{\epsilon _3}(\alpha )$. This is a contradiction since ![]() $X'$ cannot be contained in a Margulis tube. If
$X'$ cannot be contained in a Margulis tube. If ![]() $p \in Y' \smallsetminus C$ then there is an essential closed curve
$p \in Y' \smallsetminus C$ then there is an essential closed curve ![]() $\beta$ through
$\beta$ through ![]() $p$ of length
$p$ of length ![]() $\le L$ that is not homotopic to
$\le L$ that is not homotopic to ![]() $\alpha$. Then the length bound implies that
$\alpha$. Then the length bound implies that ![]() $\beta \subset T_{\epsilon _3}(\alpha )$, which is again a contradiction. It follows that
$\beta \subset T_{\epsilon _3}(\alpha )$, which is again a contradiction. It follows that ![]() $T_{\delta }(\alpha ) \cap \partial C(M) \subseteq C$.
$T_{\delta }(\alpha ) \cap \partial C(M) \subseteq C$.
To finish the proof we show that ![]() $\partial T_{\delta }(\alpha )\cap C(M)$ is connected. We can assume that
$\partial T_{\delta }(\alpha )\cap C(M)$ is connected. We can assume that ![]() $\partial T_\delta (\alpha )$ and
$\partial T_\delta (\alpha )$ and ![]() $\partial C(M)$ are transverse. (If not, we can slightly decrease
$\partial C(M)$ are transverse. (If not, we can slightly decrease ![]() $\delta$.) On
$\delta$.) On ![]() $\partial T_\delta (\alpha )$ the intersection
$\partial T_\delta (\alpha )$ the intersection ![]() $\partial T_\delta (\alpha ) \cap \partial C(M)$ will be a collection of simple closed curves that either are homotopic to
$\partial T_\delta (\alpha ) \cap \partial C(M)$ will be a collection of simple closed curves that either are homotopic to ![]() $\alpha$ or are contractible and bound disks. These curves will bound the region of
$\alpha$ or are contractible and bound disks. These curves will bound the region of ![]() $\partial T_\delta (\alpha )$ that is contained in
$\partial T_\delta (\alpha )$ that is contained in ![]() $C(M)$. We will show that it is either a pair of parallel curves homotopic to
$C(M)$. We will show that it is either a pair of parallel curves homotopic to ![]() $\alpha$ or a collection of contractible curves bounding disks whose interiors are disjoint from
$\alpha$ or a collection of contractible curves bounding disks whose interiors are disjoint from ![]() $C(M)$.
$C(M)$.
First we assume that the intersection of ![]() $\alpha '$ with the bending lamination is zero. Then the collar
$\alpha '$ with the bending lamination is zero. Then the collar ![]() $C$ is totally geodesic outside of
$C$ is totally geodesic outside of ![]() $\alpha '$ where it is bent at some angle (possibly zero). This implies that for points in
$\alpha '$ where it is bent at some angle (possibly zero). This implies that for points in ![]() $C$ the injectivity radius on
$C$ the injectivity radius on ![]() $\partial C(M)$ agrees with the injectivity radius in the ambient hyperbolic
$\partial C(M)$ agrees with the injectivity radius in the ambient hyperbolic ![]() $3$-manifold
$3$-manifold ![]() $M$ and therefore the intersection of
$M$ and therefore the intersection of ![]() $\partial C(M)$ with
$\partial C(M)$ with ![]() $T_{\delta }(\alpha )$ is the
$T_{\delta }(\alpha )$ is the ![]() $\delta$-Margulis collar about
$\delta$-Margulis collar about ![]() $\alpha$. In particular,
$\alpha$. In particular, ![]() $\partial T_\delta (\alpha ) \cap \partial C(M)$ is a pair of parallel curves and
$\partial T_\delta (\alpha ) \cap \partial C(M)$ is a pair of parallel curves and ![]() $\partial T_\delta (\alpha ) \cap C(M)$ is an annulus bounded by these curves and therefore is connected. If
$\partial T_\delta (\alpha ) \cap C(M)$ is an annulus bounded by these curves and therefore is connected. If ![]() $\alpha '$ intersects the bending lamination then we can foliate
$\alpha '$ intersects the bending lamination then we can foliate ![]() $C$ with geodesic segments in
$C$ with geodesic segments in ![]() $M$ joining the boundary components of
$M$ joining the boundary components of ![]() $C$. Note that
$C$. Note that ![]() $C$ is contained in
$C$ is contained in ![]() $T_{\epsilon _3}(\alpha )$, and as any geodesic in
$T_{\epsilon _3}(\alpha )$, and as any geodesic in ![]() $T_{\epsilon _3}(\alpha )$ will intersect
$T_{\epsilon _3}(\alpha )$ will intersect ![]() $T_\delta (\alpha )$ in a connected set we have that each geodesic arc of the foliation has connected intersection with
$T_\delta (\alpha )$ in a connected set we have that each geodesic arc of the foliation has connected intersection with ![]() $T_\delta (\alpha )$. Thus, the intersection is either empty, a point, or a closed interval. By continuity of the foliation this implies that
$T_\delta (\alpha )$. Thus, the intersection is either empty, a point, or a closed interval. By continuity of the foliation this implies that ![]() $C\cap T_{\delta }(\alpha )$ is either a union of disks or an annulus. In the annulus case,
$C\cap T_{\delta }(\alpha )$ is either a union of disks or an annulus. In the annulus case, ![]() $\partial T_\delta (\alpha )\cap C(M)$ is also an annulus and therefore is connected. For the disk case,
$\partial T_\delta (\alpha )\cap C(M)$ is also an annulus and therefore is connected. For the disk case, ![]() $Y'$ intersects
$Y'$ intersects ![]() $T_\delta (\alpha )$ in a union of disjoint disks and
$T_\delta (\alpha )$ in a union of disjoint disks and ![]() $\partial T_\delta (\alpha )\cap C(M)$ is either a union of disks or the complement of a union of disks. As
$\partial T_\delta (\alpha )\cap C(M)$ is either a union of disks or the complement of a union of disks. As ![]() $T_\delta (\alpha )\cap C(M)$ is the intersection of two convex sets, it is connected. Therefore,
$T_\delta (\alpha )\cap C(M)$ is the intersection of two convex sets, it is connected. Therefore, ![]() $\partial T_\delta (\alpha )\cap C(M)$ must be the complement of a union of disks and therefore is connected.
$\partial T_\delta (\alpha )\cap C(M)$ must be the complement of a union of disks and therefore is connected.
5.4 Proof of Proposition 5.3
We now are ready to prove Proposition 5.3, which will complete the proof that the auxiliary components do not contribute to the limiting model flow. We restate it.
Proposition 5.3 There exists ![]() $\delta > 0$ such that the following assertion holds. Given
$\delta > 0$ such that the following assertion holds. Given ![]() $\eta,K>0$, there exists a
$\eta,K>0$, there exists a ![]() $\epsilon >0$ such that if
$\epsilon >0$ such that if ![]() $\operatorname {Re}{\mathcal {L}}_\alpha (M_Y) \le 2\delta$ and
$\operatorname {Re}{\mathcal {L}}_\alpha (M_Y) \le 2\delta$ and ![]() ${{\rm Vol}_C}(M_Y) \le K$ then
${{\rm Vol}_C}(M_Y) \le K$ then
Proof. The support of ![]() $\big (\mu ^{<\epsilon }\big )^{\rm aux}_{T}$ is contained in the union of
$\big (\mu ^{<\epsilon }\big )^{\rm aux}_{T}$ is contained in the union of ![]() $S_\epsilon ^\alpha (\beta )$ where
$S_\epsilon ^\alpha (\beta )$ where ![]() $\beta$ ranges over the closed geodesics of length
$\beta$ ranges over the closed geodesics of length ![]() $< 2\epsilon$ in
$< 2\epsilon$ in ![]() $Y$. There are at most
$Y$. There are at most ![]() $3g-3$ such curves, where
$3g-3$ such curves, where ![]() $g$ is the genus of
$g$ is the genus of ![]() $Y$, so it will be enough to bound the area of the individual
$Y$, so it will be enough to bound the area of the individual ![]() $S_\epsilon ^\alpha (\beta )$.
$S_\epsilon ^\alpha (\beta )$.
Fix ![]() $\delta >0$ as in Lemma 5.12 and choose
$\delta >0$ as in Lemma 5.12 and choose ![]() $\tilde x \in {{\mathbb {H}}^3}$ that maps to
$\tilde x \in {{\mathbb {H}}^3}$ that maps to ![]() $x \in M^{\ge \epsilon _3} \cap \partial C(M)$ under the covering map
$x \in M^{\ge \epsilon _3} \cap \partial C(M)$ under the covering map ![]() ${{\mathbb {H}}^3} \to M_Y$. Then by Lemmas 5.9 and 5.10 we have, for
${{\mathbb {H}}^3} \to M_Y$. Then by Lemmas 5.9 and 5.10 we have, for ![]() $\alpha,\beta$ of length less than
$\alpha,\beta$ of length less than ![]() $2\delta$,
$2\delta$,
where ![]() $D$ is a the diameter bound on
$D$ is a the diameter bound on ![]() $C(M_Y)^{<\delta }$ and
$C(M_Y)^{<\delta }$ and ![]() $N$ depends on
$N$ depends on ![]() $D$. By Lemma 5.11, the diameter of each component of
$D$. By Lemma 5.11, the diameter of each component of ![]() $C(M_Y)^{<\delta }$ is bounded by a constant only depending on the volume of
$C(M_Y)^{<\delta }$ is bounded by a constant only depending on the volume of ![]() $C(M_Y)$. By Lemma 5.12,
$C(M_Y)$. By Lemma 5.12, ![]() $C(M_Y)^{< \delta }$ is connected. Therefore,
$C(M_Y)^{< \delta }$ is connected. Therefore, ![]() $D$, and hence
$D$, and hence ![]() $N$, only depend on the volume of
$N$, only depend on the volume of ![]() $C(M_Y)$ and the sum only depends on the volume of
$C(M_Y)$ and the sum only depends on the volume of ![]() $C(M_Y)$. The result then follows from Corollary 5.7 by further choosing
$C(M_Y)$. The result then follows from Corollary 5.7 by further choosing ![]() $2\delta < \delta _0$ so that
$2\delta < \delta _0$ so that ![]() $\operatorname {Re}{\mathcal {L}}_\alpha (M_Y) <\delta _0$.
$\operatorname {Re}{\mathcal {L}}_\alpha (M_Y) <\delta _0$.
6. Vector field at infinity
We now return to our flowline ![]() $Y_t$ of the gradient vector field
$Y_t$ of the gradient vector field ![]() $V$ on
$V$ on ![]() $\operatorname {Teich}(S)$ and recall that by Theorem 3.2 we have
$\operatorname {Teich}(S)$ and recall that by Theorem 3.2 we have ![]() $Y_t \to \hat Y \in \operatorname {Teich}(S)$ and
$Y_t \to \hat Y \in \operatorname {Teich}(S)$ and ![]() $\|V(Y_t)\|_2 = \|\phi _{Y_t}\|_2 \to 0$. The surface
$\|V(Y_t)\|_2 = \|\phi _{Y_t}\|_2 \to 0$. The surface ![]() $\hat Y$ is a noded surface (with possibly empty nodal set). We can assume that
$\hat Y$ is a noded surface (with possibly empty nodal set). We can assume that ![]() $\alpha$ is one of the nodes and let
$\alpha$ is one of the nodes and let ![]() $c_\alpha (t) = \ell _\alpha (Y_t)/{\mathcal {L}}_\alpha (M_{Y_t}).$ Then, by Theorem 4.10, if
$c_\alpha (t) = \ell _\alpha (Y_t)/{\mathcal {L}}_\alpha (M_{Y_t}).$ Then, by Theorem 4.10, if ![]() $t_n\to \infty$ is a subsequence with
$t_n\to \infty$ is a subsequence with ![]() $c_\alpha (t_n)\to c$ for some
$c_\alpha (t_n)\to c$ for some ![]() $c \in \mathbb {C}$ we have
$c \in \mathbb {C}$ we have ![]() $c'_\alpha (t) \to v(c)$ where
$c'_\alpha (t) \to v(c)$ where ![]() $v$ is the vector field
$v$ is the vector field
shown in Figure 6.
Proposition 6.1 The critical points of the vector field ![]() $v(z)$ are
$v(z)$ are ![]() $z=0$ (unstable),
$z=0$ (unstable), ![]() $z= 1$ (stable),
$z= 1$ (stable), ![]() $z=2$ (saddle), and
$z=2$ (saddle), and ![]() $z=-1$ (saddle). The basin of attraction of
$z=-1$ (saddle). The basin of attraction of ![]() $z=1$ is the disk
$z=1$ is the disk ![]() $|z-1| < 1$, and the circle
$|z-1| < 1$, and the circle ![]() $|z-1| = 1$ consists of two trajectories from
$|z-1| = 1$ consists of two trajectories from ![]() $0$ to
$0$ to ![]() $2$.
$2$.

Figure 6. Vector field ![]() $v(z) =\tfrac {1}{4}\big (|z|^4-2z\operatorname {Re}(z^2)-z^2+2z\big )$.
$v(z) =\tfrac {1}{4}\big (|z|^4-2z\operatorname {Re}(z^2)-z^2+2z\big )$.
Proof. A direct computation shows that ![]() $v(-1)=v(0) = v(1) = v(2) = 0$ and that there are no other zeros. The linearization of each zero is non-trivial and gives that each zero of
$v(-1)=v(0) = v(1) = v(2) = 0$ and that there are no other zeros. The linearization of each zero is non-trivial and gives that each zero of ![]() $v$ is as described. Once we show that the circle
$v$ is as described. Once we show that the circle ![]() $|z-1| =1$ consists of two trajectories from
$|z-1| =1$ consists of two trajectories from ![]() $0$ to
$0$ to ![]() $2$ it will follow that
$2$ it will follow that ![]() $|z-1|<1$ is the basin of attraction for
$|z-1|<1$ is the basin of attraction for ![]() $z=1$ as there are exactly two trajectories limiting to the unstable fixed point at
$z=1$ as there are exactly two trajectories limiting to the unstable fixed point at ![]() $z=2$ and therefore all the other trajectories in the disk must limit to
$z=2$ and therefore all the other trajectories in the disk must limit to ![]() $z=1$ (since they cannot limit to the unstable fixed point at
$z=1$ (since they cannot limit to the unstable fixed point at ![]() $z=0$).
$z=0$).
If we let ![]() $w(z) = (z-1)/|z-1|$ be the radial vector field centered at
$w(z) = (z-1)/|z-1|$ be the radial vector field centered at ![]() $z=1$ then the Euclidean inner product of
$z=1$ then the Euclidean inner product of ![]() $v$ and
$v$ and ![]() $w$ is given by taking the real part of the product of
$w$ is given by taking the real part of the product of ![]() $v$ and the conjugate of
$v$ and the conjugate of ![]() $w$ (as functions). Points in the circle
$w$ (as functions). Points in the circle ![]() $|z-1| = 1$ are of the form
$|z-1| = 1$ are of the form ![]() $z = 1 + e^{i\theta }$ and on calculates to see that
$z = 1 + e^{i\theta }$ and on calculates to see that ![]() $\langle v(z), w(z) \rangle = 0$ for such points so
$\langle v(z), w(z) \rangle = 0$ for such points so ![]() $v$ is tangent to this circle.
$v$ is tangent to this circle.
On the other hand, if we let ![]() $h(z)= 1$ be the constant horizontal vector field then on the circle we have
$h(z)= 1$ be the constant horizontal vector field then on the circle we have
This is zero only when ![]() $z$ is
$z$ is ![]() $0$ or
$0$ or ![]() $2$ (and
$2$ (and ![]() $\theta$ is
$\theta$ is ![]() $\pi$ or
$\pi$ or ![]() $0$) and is positive otherwise. This implies that
$0$) and is positive otherwise. This implies that ![]() $z=0$ and
$z=0$ and ![]() $z=2$ are the only critical points on the circle and that the flowlines are from
$z=2$ are the only critical points on the circle and that the flowlines are from ![]() $0$ to
$0$ to ![]() $2$ as claimed.
$2$ as claimed.
We will use the next lemma to analyze the limiting behavior of the path ![]() $c_\alpha$.
$c_\alpha$.
Lemma 6.2 Let ![]() $v$ be a smooth vector field on
$v$ be a smooth vector field on ![]() $\mathbb {R}^n$ and
$\mathbb {R}^n$ and ![]() $\gamma \colon [0,\infty ) \to \mathbb {R}^n$ be a smooth path whose image lies in a compact subset. Also assume that
$\gamma \colon [0,\infty ) \to \mathbb {R}^n$ be a smooth path whose image lies in a compact subset. Also assume that ![]() $\gamma '(t_n) \to v(p)$ for all sequences
$\gamma '(t_n) \to v(p)$ for all sequences ![]() $t_n$ with
$t_n$ with ![]() $\gamma (t_n)$ converging to some
$\gamma (t_n)$ converging to some ![]() $p\in \mathbb {R}^n$.
$p\in \mathbb {R}^n$.
Let ![]() $\mathcal {A}$ be the accumulation set for
$\mathcal {A}$ be the accumulation set for ![]() $\gamma$. Then
$\gamma$. Then ![]() $\mathcal {A}$ is a union of trajectories of the flow of
$\mathcal {A}$ is a union of trajectories of the flow of ![]() $v$.
$v$.
If ![]() ${\mathcal {A}}$ contains distinct points
${\mathcal {A}}$ contains distinct points ![]() $p$ and
$p$ and ![]() $q$ then there exists an
$q$ then there exists an ![]() $\epsilon >0$ such that if
$\epsilon >0$ such that if ![]() $\delta <\epsilon$ then there is a trajectory
$\delta <\epsilon$ then there is a trajectory ![]() $\beta \in {\mathcal {A}}$ and a
$\beta \in {\mathcal {A}}$ and a ![]() $t \in \mathbb {R}$ such that
$t \in \mathbb {R}$ such that ![]() $|\beta (t) - p| = \delta$ and
$|\beta (t) - p| = \delta$ and ![]() $\langle w, \beta '(t) \rangle \ge 0$, and similarly a trajectory with
$\langle w, \beta '(t) \rangle \ge 0$, and similarly a trajectory with ![]() $\langle w, \beta '(t) \rangle \le 0$. In particular, if
$\langle w, \beta '(t) \rangle \le 0$. In particular, if ![]() $p \in {\mathcal {A}}$ is an attracting or repelling fixed point of
$p \in {\mathcal {A}}$ is an attracting or repelling fixed point of ![]() $v$ or
$v$ or ![]() $p$ is an isolated point of
$p$ is an isolated point of ![]() ${\mathcal {A}}$ then
${\mathcal {A}}$ then ![]() ${\mathcal {A}} = \{p\}$ and
${\mathcal {A}} = \{p\}$ and ![]() $\gamma (t) \to p$.
$\gamma (t) \to p$.
Proof. Since the image of ![]() $\gamma$ has compact support we can assume that
$\gamma$ has compact support we can assume that ![]() $v$ has compact support and
$v$ has compact support and ![]() $|v|$ is bounded. We first show that
$|v|$ is bounded. We first show that ![]() $|\gamma '(t) - v(\gamma (t))| \to 0$ as
$|\gamma '(t) - v(\gamma (t))| \to 0$ as ![]() $t\to \infty$. If not we can find a sequence
$t\to \infty$. If not we can find a sequence ![]() $t_n \to \infty$ such that
$t_n \to \infty$ such that ![]() $\gamma (t_n) \to p$ in
$\gamma (t_n) \to p$ in ![]() $M$ but
$M$ but ![]() $|\gamma '(t_n) - v(\gamma (t_n))|$ converges to some non-zero
$|\gamma '(t_n) - v(\gamma (t_n))|$ converges to some non-zero ![]() $s \in \mathbb {R}$. But by assumption
$s \in \mathbb {R}$. But by assumption ![]() $\gamma '(t_n) \to v(p)$ which implies
$\gamma '(t_n) \to v(p)$ which implies ![]() $|\gamma '(t_n) - v(\gamma (t_n))| \to 0$, a contradiction.
$|\gamma '(t_n) - v(\gamma (t_n))| \to 0$, a contradiction.
Therefore, ![]() $\gamma '(t)$ is bounded. Now let
$\gamma '(t)$ is bounded. Now let ![]() $\gamma _\tau (t) = \gamma (t+\tau )$ and for
$\gamma _\tau (t) = \gamma (t+\tau )$ and for ![]() $p\in \mathcal {A}$ choose a sequence
$p\in \mathcal {A}$ choose a sequence ![]() $\tau _i\to \infty$ with
$\tau _i\to \infty$ with ![]() $\gamma _{\tau _i}(0) \to p$. As the
$\gamma _{\tau _i}(0) \to p$. As the ![]() $\gamma '_\tau$ are also bounded, by Arzelà–Ascoli (after possibly passing to a subsequence), we have a locally uniform limit
$\gamma '_\tau$ are also bounded, by Arzelà–Ascoli (after possibly passing to a subsequence), we have a locally uniform limit ![]() $\gamma _i(t) = \gamma _{\tau _i} \to \beta$ and
$\gamma _i(t) = \gamma _{\tau _i} \to \beta$ and ![]() $\gamma '_{\tau _i}(t)$ limits locally uniformly to
$\gamma '_{\tau _i}(t)$ limits locally uniformly to ![]() $v(\beta (t))$. Note that
$v(\beta (t))$. Note that ![]() $\beta$ is defined on all of
$\beta$ is defined on all of ![]() $\mathbb {R}$. Therefore, we have
$\mathbb {R}$. Therefore, we have
 \begin{align*} \beta(0) + \int_0^t v(\beta(s))\,ds & = \gamma_i(t) - \left(\gamma_i(0) + \int_0^t \gamma'_i(s) \,ds\right) + \beta(0) + \int_0^t v(\beta(s))\,ds\\ & = \lim_{i\to \infty}\left(\gamma_i(t) +\big(\beta(0) -\gamma_i(0)\big) + \int_0^t \big(v(\beta(s)) - \gamma'_i(s)\big) \,ds\right)\\ & = \beta(t) \end{align*}
\begin{align*} \beta(0) + \int_0^t v(\beta(s))\,ds & = \gamma_i(t) - \left(\gamma_i(0) + \int_0^t \gamma'_i(s) \,ds\right) + \beta(0) + \int_0^t v(\beta(s))\,ds\\ & = \lim_{i\to \infty}\left(\gamma_i(t) +\big(\beta(0) -\gamma_i(0)\big) + \int_0^t \big(v(\beta(s)) - \gamma'_i(s)\big) \,ds\right)\\ & = \beta(t) \end{align*}
which implies that ![]() $\beta$ is a trajectory of
$\beta$ is a trajectory of ![]() $v$. Note that the image of
$v$. Note that the image of ![]() $\beta$ will be contained in
$\beta$ will be contained in ![]() $\mathcal {A}$, so we have shown that
$\mathcal {A}$, so we have shown that ![]() $\mathcal {A}$ is a union of trajectories.
$\mathcal {A}$ is a union of trajectories.
For the final statement let ![]() $\epsilon = |p-q|/3$. Then for any
$\epsilon = |p-q|/3$. Then for any ![]() $\delta >0$ the path
$\delta >0$ the path ![]() $\gamma$ must leave and enter any ball of radius
$\gamma$ must leave and enter any ball of radius ![]() $\delta <\epsilon$ centered at
$\delta <\epsilon$ centered at ![]() $p$ infinitely often. Therefore, we can find
$p$ infinitely often. Therefore, we can find ![]() $t_n\to \infty$ such that
$t_n\to \infty$ such that ![]() $|\gamma (t_n) - p| = \delta$ and
$|\gamma (t_n) - p| = \delta$ and ![]() $\langle w, \gamma '(t_n)\rangle \ge 0$. After possibly passing to a subsequence there is a trajectory
$\langle w, \gamma '(t_n)\rangle \ge 0$. After possibly passing to a subsequence there is a trajectory ![]() $\beta \in {\mathcal {A}}$ with
$\beta \in {\mathcal {A}}$ with ![]() $\gamma (t_n)\to \beta (t)$ and
$\gamma (t_n)\to \beta (t)$ and ![]() $\gamma '(t_n) \to \beta '(t)$. Continuity implies that
$\gamma '(t_n) \to \beta '(t)$. Continuity implies that ![]() $|\beta (t) - p| = \delta$ and
$|\beta (t) - p| = \delta$ and ![]() $\langle w, \beta '(t)\rangle \ge 0$ as claimed. The other inequality follows similarly.
$\langle w, \beta '(t)\rangle \ge 0$ as claimed. The other inequality follows similarly.
We can now show that ![]() $c_\alpha (t)$ converges to
$c_\alpha (t)$ converges to ![]() $1$.
$1$.
Proposition 6.3 As ![]() $t\to \infty$ we have
$t\to \infty$ we have ![]() $c_\alpha (t) \to 1$.
$c_\alpha (t) \to 1$.
Proof. Let ![]() ${\mathcal {C}}$ be the accumulation set of
${\mathcal {C}}$ be the accumulation set of ![]() $c_\alpha$. As
$c_\alpha$. As ![]() $c_\alpha (t)$ is contained in the disk
$c_\alpha (t)$ is contained in the disk ![]() $|z-1| \le 1$, we must have that all of the trajectories in
$|z-1| \le 1$, we must have that all of the trajectories in ![]() ${\mathcal {C}}$ are contained in this disk. Note that any non-constant trajectory in the disk contains either
${\mathcal {C}}$ are contained in this disk. Note that any non-constant trajectory in the disk contains either ![]() $0$ or
$0$ or ![]() $1$ (and often both) in its closure, so if
$1$ (and often both) in its closure, so if ![]() ${\mathcal {C}}$ contains a non-constant trajectory then it contains either
${\mathcal {C}}$ contains a non-constant trajectory then it contains either ![]() $0$ or
$0$ or ![]() $1$, and by the second part of Lemma 6.2 we then have
$1$, and by the second part of Lemma 6.2 we then have ![]() ${\mathcal {C}} = \{0\}$ or
${\mathcal {C}} = \{0\}$ or ![]() ${\mathcal {C}} = \{1\}$. In particular,
${\mathcal {C}} = \{1\}$. In particular, ![]() ${\mathcal {C}}$ cannot contain any non-constant trajectories and therefore, again by the second part of Lemma 6.2, must be equal to one of the zeros of
${\mathcal {C}}$ cannot contain any non-constant trajectories and therefore, again by the second part of Lemma 6.2, must be equal to one of the zeros of ![]() $v$ in the disk
$v$ in the disk ![]() $|z-1| \le 1$. We finish the proof by showing that
$|z-1| \le 1$. We finish the proof by showing that ![]() $c_\alpha (t)$ does not converge to
$c_\alpha (t)$ does not converge to ![]() $0$ or
$0$ or ![]() $2$.
$2$.
If as ![]() $t\to \infty$ we have
$t\to \infty$ we have ![]() $c_\alpha (t) \to 0$, then for
$c_\alpha (t) \to 0$, then for ![]() $f(t) = \operatorname {Re}(\log (c_\alpha (t))$ we have
$f(t) = \operatorname {Re}(\log (c_\alpha (t))$ we have ![]() $f(t) \to -\infty$. But by Theorem 4.10,
$f(t) \to -\infty$. But by Theorem 4.10,
As ![]() $f'(t) = \operatorname {Re}(c_\alpha '(t)/c_\alpha (t))$ it follows that
$f'(t) = \operatorname {Re}(c_\alpha '(t)/c_\alpha (t))$ it follows that ![]() $f(t)$ is increasing for
$f(t)$ is increasing for ![]() $t$, contradicting that
$t$, contradicting that ![]() $\lim _{t\rightarrow \infty }f(t)= -\infty$. Thus,
$\lim _{t\rightarrow \infty }f(t)= -\infty$. Thus, ![]() $\lim _{t\to \infty } c_\alpha (t) \neq 0$.
$\lim _{t\to \infty } c_\alpha (t) \neq 0$.
If ![]() $c_\alpha (t) \rightarrow 2$ as
$c_\alpha (t) \rightarrow 2$ as ![]() $t\rightarrow \infty$ then by (1) of Theorem 4.10 we have
$t\rightarrow \infty$ then by (1) of Theorem 4.10 we have
for all sequences ![]() $t_n\to \infty$. On the other hand, as
$t_n\to \infty$. On the other hand, as ![]() $\ell _\alpha (t)\to 0$ as
$\ell _\alpha (t)\to 0$ as ![]() $t\rightarrow \infty$, we can choose a subsequence such that
$t\rightarrow \infty$, we can choose a subsequence such that ![]() $\ell _\alpha '(t_n)\leq 0$ and therefore
$\ell _\alpha '(t_n)\leq 0$ and therefore
This is a contradiction, and therefore ![]() $\lim _{t\to \infty }c_\alpha (t) \neq 2$. It follows that
$\lim _{t\to \infty }c_\alpha (t) \neq 2$. It follows that ![]() $\lim _{t\to \infty }c_\alpha (t) = 1$.
$\lim _{t\to \infty }c_\alpha (t) = 1$.
7. Main theorem
Before we finish the proof of the main theorem, we will need the following bound on the ![]() $L^\infty$-norm of a harmonic Beltrami differential in terms of the
$L^\infty$-norm of a harmonic Beltrami differential in terms of the ![]() $L^2$-norm and the derivative of the length of short geodesics.
$L^2$-norm and the derivative of the length of short geodesics.
Lemma 7.1 (Wolpert [Reference WolpertWol17, Lemma 11])
There exists an ![]() $\epsilon _0$ satisfying the following assertion. Given
$\epsilon _0$ satisfying the following assertion. Given ![]() $\epsilon < \epsilon _0$, there exists
$\epsilon < \epsilon _0$, there exists ![]() $c >0$ such that if
$c >0$ such that if ![]() $\tau$ is the family of geodesics with
$\tau$ is the family of geodesics with ![]() $\ell _\alpha < \epsilon$ for
$\ell _\alpha < \epsilon$ for ![]() $\alpha \in \tau$ and
$\alpha \in \tau$ and ![]() $\mu$ is a harmonic Beltrami differential on
$\mu$ is a harmonic Beltrami differential on ![]() $Y$ then
$Y$ then
where ![]() $\mu _0$ is the component of
$\mu _0$ is the component of ![]() $\mu$ orthogonal (in the Weil–Petersson inner product) to the span of the of the gradients
$\mu$ orthogonal (in the Weil–Petersson inner product) to the span of the of the gradients ![]() $\nabla \ell _\alpha$.
$\nabla \ell _\alpha$.
Wolpert's original bound is in terms of the gradient of the root-length functions ![]() $\ell _{\alpha }^{1/2}$. One can translate his statement to the above statement via the chain rule.
$\ell _{\alpha }^{1/2}$. One can translate his statement to the above statement via the chain rule.
The above gives the following immediate corollary.
Corollary 7.2 Let ![]() $(N;S)$ be relatively acylindrical and
$(N;S)$ be relatively acylindrical and ![]() $M_t \in CC(N;S,X)$ be a flowline for
$M_t \in CC(N;S,X)$ be a flowline for ![]() $V$, with quadratic differential
$V$, with quadratic differential ![]() $\phi _t$. Then
$\phi _t$. Then
Proof. We have ![]() $Y_t \rightarrow Y_\tau$ where
$Y_t \rightarrow Y_\tau$ where ![]() $\tau$ is the collection of nodes. Then there is an
$\tau$ is the collection of nodes. Then there is an ![]() $\epsilon _1 >0$ such that if
$\epsilon _1 >0$ such that if ![]() $\ell _\beta (Y_t) < \epsilon _1$ then
$\ell _\beta (Y_t) < \epsilon _1$ then ![]() $\beta \in \tau$. We apply the above to
$\beta \in \tau$. We apply the above to ![]() $\mu = V_t = -\overline \phi _t/\rho _{Y_t}$ for
$\mu = V_t = -\overline \phi _t/\rho _{Y_t}$ for ![]() $\epsilon < \min (\epsilon _0,\epsilon _1)$. As
$\epsilon < \min (\epsilon _0,\epsilon _1)$. As ![]() $\|\mu _0\|_2 \leq \|\mu \|_2$, we have
$\|\mu _0\|_2 \leq \|\mu \|_2$, we have
By Proposition 6.3, ![]() $\lim _{t\rightarrow \infty } c_\alpha (t) = c_\alpha = 1$. Thus, by Theorem 4.10,
$\lim _{t\rightarrow \infty } c_\alpha (t) = c_\alpha = 1$. Thus, by Theorem 4.10,
Thus, as ![]() $\lim _{t\rightarrow \infty }\|\phi _t\|_2 = 0$ the result follows.
$\lim _{t\rightarrow \infty }\|\phi _t\|_2 = 0$ the result follows.
We now have everything in place to prove our main result.
Theorem 1.1 Let ![]() $(N;S)$ be relatively acylindrical and
$(N;S)$ be relatively acylindrical and ![]() $M_t \in CC(N;S,X)$ be a flowline for
$M_t \in CC(N;S,X)$ be a flowline for ![]() $V$. Then
$V$. Then ![]() $M_t$ converges to
$M_t$ converges to ![]() $M_{\rm geod}.$
$M_{\rm geod}.$
Proof. If ![]() $Y_t$ is the corresponding flowline of
$Y_t$ is the corresponding flowline of ![]() $V$ on
$V$ on ![]() $\operatorname {Teich}(S)$ we have that
$\operatorname {Teich}(S)$ we have that ![]() $M_t = M_{Y_t}$. We let
$M_t = M_{Y_t}$. We let ![]() $\phi _t$ be the quadratic differential given by the Schwarzian on
$\phi _t$ be the quadratic differential given by the Schwarzian on ![]() $Y_t$. Then by Theorem 3.2 we have that
$Y_t$. Then by Theorem 3.2 we have that ![]() $Y_t \rightarrow \hat Y$ where
$Y_t \rightarrow \hat Y$ where ![]() $\hat Y$ is a possibly noded surface in the Weil–Petersson completion
$\hat Y$ is a possibly noded surface in the Weil–Petersson completion ![]() $\overline {\operatorname {Teich}(S)}$. We will show that the set of nodes is empty as the
$\overline {\operatorname {Teich}(S)}$. We will show that the set of nodes is empty as the ![]() $\hat Y$ is actually contained in
$\hat Y$ is actually contained in ![]() $\operatorname {Teich}(S)$.
$\operatorname {Teich}(S)$.
We let ![]() $\sigma = \sigma _{(N;S)}:\operatorname {Teich}(S)\rightarrow \operatorname {Teich}(S)$ be the restriction of the skinning map to
$\sigma = \sigma _{(N;S)}:\operatorname {Teich}(S)\rightarrow \operatorname {Teich}(S)$ be the restriction of the skinning map to ![]() $S \subseteq \partial N$.
$S \subseteq \partial N$.
By McMullen, the skinning map is contracting in the Teichmüller metric ![]() $d_{\operatorname {Teich}}$ with contraction factor
$d_{\operatorname {Teich}}$ with contraction factor ![]() $c <1$ depending only on the topology of
$c <1$ depending only on the topology of ![]() $(N;S)$ (see [Reference McMullenMcM90, Theorem 6,1 and Corollary 6.2]). It follows that there is a unique fixed point of
$(N;S)$ (see [Reference McMullenMcM90, Theorem 6,1 and Corollary 6.2]). It follows that there is a unique fixed point of ![]() $\sigma$ which we label
$\sigma$ which we label ![]() $Y_{\rm geod}$ since
$Y_{\rm geod}$ since ![]() $M_{\rm geod} = M_{Y_{\rm geod}}$.
$M_{\rm geod} = M_{Y_{\rm geod}}$.
For any contraction mapping we can bound the distance from a point to the fixed point in terms of the distance between the point and its first iterate. In particular, for any ![]() $Y_t$ we have
$Y_t$ we have
By the Ahlfors–Weill quasiconformal reflection theorem (see [Reference Ahlfors and WeillAW62, Theorem A]) if ![]() $\|\phi _t\|_\infty <1/2$ then
$\|\phi _t\|_\infty <1/2$ then
By Corollary 7.2, ![]() $\lim _{t\rightarrow \infty }\|\phi _t\| \rightarrow 0$. so we can combine the two inequalities to get
$\lim _{t\rightarrow \infty }\|\phi _t\| \rightarrow 0$. so we can combine the two inequalities to get ![]() $\lim _{t\to \infty }d_{\operatorname {Teich}}(Y_t ,Y_{\rm geod}) =0$. Therefore,
$\lim _{t\to \infty }d_{\operatorname {Teich}}(Y_t ,Y_{\rm geod}) =0$. Therefore, ![]() $M_t \to M_{\rm geod}$ as claimed.
$M_t \to M_{\rm geod}$ as claimed.
Acknowledgements
We would like to thank MSRI for their hospitality while portions of this work were being completed. We also thank D. Dumas and C. McMullen for helpful conversations. Finally, we would like to especially thank the reviewer whose comments and suggestions greatly improved the paper.