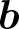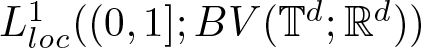1. Introduction
Consider a bounded, divergence-free vector field 
$\boldsymbol{b}:[0,1]\times\mathbb{T}^d\to \mathbb{R}^d$. The superposition principle (see Theorem 1.4) guarantees existence of a measure concentrated on integral curves of 
$\boldsymbol{b}$, whose 1-marginals at every time is the Lebesgue measure on 
$\mathbb{T}^d$.
Question 1. Is there a robust selection criterion amongst all such measures?
When 
$\boldsymbol{b}$ lies in 
$L^1((0,1);BV(\mathbb{T}^d;\mathbb{R}^d))$, Ambrosio [Reference Ambrosio2] following on DiPerna and Lions [Reference DiPerna and Lions9] proved that there exists a unique such measure, thereby answering the above question affirmatively. In this work, we give an affirmative answer to the above question for a class of bounded, divergence-free vector fields to which the work of Ambrosio does not apply. Let us introduce the main objects of study.
All vector fields 
$\boldsymbol{b}:[0,1]\times\mathbb{T}^d\to\mathbb{R}^d$ will be Borel, essentially bounded and divergence-free, meaning that
\begin{equation*}\operatorname{div}_x\boldsymbol{b} =0 \qquad\text{in the sense of distributions on }\; [0,1]\times\mathbb{T}^d.\end{equation*} Let us define integral curves of 
$\boldsymbol{b}$.
Definition 1.1. We shall say that a curve 
$\gamma:[0,1]\to \mathbb{T}^d$ is an integral curve of 
$\boldsymbol{b}$, if it is an absolutely continuous solution to the ODE
\begin{equation*}\dot{\gamma}(t)=\boldsymbol{b}(t,\gamma(t)),\end{equation*} which means explicitely that for every 
$s,t\in[0,1]$
\begin{equation*}
\gamma(t)-\gamma(s)=\int_s^t\boldsymbol{b}(\tau,\gamma(\tau))d\tau \qquad\text{and} \qquad \int_0^1|\boldsymbol{b}(\tau,\gamma(\tau))|d\tau \lt +\infty.
\end{equation*} We shall further say that 
$\gamma$ is an integral curve starting from 
$x$ at time 
$s$, if 
$\gamma(s)=x$ and we shall write 
$\gamma_{s,x}.$
Let 
$\Gamma$ denote the metric space 
$C([0,1];\mathbb{T}^d)$ of continuous paths endowed with the uniform metric, and let 
$\mathscr{M}$ denote the corresponding Borel 
$\sigma$-algebra. We recall that a selection of integral curves 
$\{\gamma_{s,x}:x\in\mathbb{T}^d\}$ is measurable, if the map 
$\mathbb{T}^d\ni x\longmapsto \gamma_{s,x}\in\Gamma$ is Borel. Ambrosio proposed the following definition in [Reference Ambrosio2].
Definition 1.2. A measurable selection 
$\{\gamma_{s,x}:x\in\mathbb{T}^d\}$ of integral curves of 
$\boldsymbol{b}$ is said to be a regular measurable selection, if there exists 
$C \gt 0$ such that
\begin{equation}
\Big|\int_{\mathbb{T}^d}\phi(\gamma_{s,x}(t))dx\Big|\leq C \Big|\int_{\mathbb{T}^d}\phi(y)dy\Big|\qquad\forall \phi\in C_c(\mathbb{T}^d),\;\forall t\in[0,1].
\end{equation} When 
$\boldsymbol{b}$ belongs to 
$ L^1((0,1);BV(\mathbb{T}^d;\mathbb{R}^d))$, and satisfies 
$\int_0^1\|[\operatorname{div}_x\boldsymbol{b}(s,\cdot)]_-\|_{L^\infty_x}ds \lt +\infty$, Ambrosio proved the existence of a regular measurable selection and the following essential uniqueness result: any two regular measurable selection 
$\{\gamma^1_{s,x}\}$ and 
$\{\gamma^2_{s,x}\}$Footnote 1 of integral curves of 
$\boldsymbol{b}$ must coincide up to a set of vanishing Lebesgue measure. Moreover, if 
$\boldsymbol{b}$ is divergence-free, the essentially unique regular measurable selection is measure-preserving in the sense that
\begin{equation}
\int_{\mathbb{T}^d}\phi(\gamma_{s,x}(t))dx=\int_{\mathbb{T}^d}\phi(y)dy\qquad\forall \phi\in C_c(\mathbb{T}^d),\;\forall t\in[0,1].
\end{equation} Recently, Pappalettera constructed in [Reference Pappaleterra12] a divergence-free vector field 
$\boldsymbol{b}$ for which there does not exist a measure-preserving selection of characteristics. This vector field does not belong to 
$L^1((0,1);BV(\mathbb{T}^d;\mathbb{R}^d))$. This, however does not exclude that for 
$\mathscr{L}^{d}$-a.e. 
$x\in\mathbb{T}^d$, a probability measure concentrated on integral curves of 
$\boldsymbol{b}$ starting from 
$x$ at time 
$0$ can be uniquely selected by some appropriate criterion. The present work investigates such a selection criterion for divergence-free vector fields in 
$L_{loc}^1((0,1];BV(\mathbb{T}^d;\mathbb{R}^d))$. For this class of vector fields, a selection criterion for solutions of the continuity equation using regularisation by convolution was already proved by the author in [Reference Pitcho13] (see also [Reference Mescolini, Pitcho and Sorella11]). We here give a Lagrangian counterpart to this previous result. We begin by defining the measures on integral curves we shall study.
1.1. Lagrangian representations
All measures are Radon measures in this work. We will denote by 
$e_t:\Gamma \ni \gamma \longmapsto\gamma(t)\in \mathbb{T}^d$ the evaluation map. We will also denote by 
$\rho:[0,1]\times\mathbb{T}^d\to \mathbb{R}^+$ a bounded density. It will always be assumed in 
$C([0,1];w^*-L^\infty(\mathbb{T}^d))$, which we may do without loss of generality, when the vector field 
$\rho(1,\boldsymbol{b})$ solves
\begin{equation}
\operatorname{div}_{t,x}\rho(1,\boldsymbol{b})=0\qquad \text{in the sense of distributions on}~[0,1]\times\mathbb{T}^d.
\end{equation}A proof of this fact is given in [Reference Pitcho13]. Let us now define the main object under consideration in this paper.
Definition 1.3. We shall say that a bounded, positive measure 
$\boldsymbol{\eta}$ on 
$\Gamma$ is a Lagrangian representation of the vector field 
$\rho(1,\boldsymbol{b})$, if the following conditions hold:
(1)
$\boldsymbol{\eta}$ is concentrated on the set
$\Gamma$ of integral curves of
$\boldsymbol{b}$, which explicitely means that for every
$s,t\in [0,1]$
\begin{equation*}
\int_\Gamma\Big|\gamma(t)-\gamma(s)-\int_s^t\boldsymbol{b}(\tau,\gamma(\tau))d\tau\Big|\boldsymbol{\eta}(d\gamma)=0;
\end{equation*}(2) for every
$t\in[0,1]$, we have
(1.3)\begin{equation}
\rho(t,\cdot)\mathscr{L}^{d}=(e_t)_\#\boldsymbol{\eta}.
\end{equation}
We now record the following general existence theorem for Lagrangian representations due to Smirnov [Reference Smirnov14] or Ambrosio and Crippa [Reference Ambrosio and Crippa3].
Theorem 1.4 (Superposition principle)
In the context of this paragraph, and assuming that 
$\rho(1,\boldsymbol{b})$ solves (PDE), there exists a Lagrangian representation of 
$\rho(1,\boldsymbol{b})$.
The above theorem is proved (see for instance [Reference Ambrosio and Crippa3]) by a regularisation and compactness argument, where the hypothesis that 
$\rho$ is non-negative plays an essential role. Let us now introduce the set of Lipschitz paths with constant 
$L \gt 0$
\begin{equation}
\Gamma_L:=\Big\{\gamma\in \Gamma\;:\;|\gamma(s)-\gamma(t)|\leq L|s-t| \quad\forall s,t\in [0,1]\Big\}.
\end{equation}Remark 1.5. 
$\Gamma_L$ is a compact, separable metric space with the metric induced from 
$\Gamma$.
For simplicity, we will now write 
$\Gamma_{\boldsymbol{b}}:= \Gamma_{\|\boldsymbol{b}\|_{L^\infty_{t,x}}}.$ We then have the following lemma.
Lemma 1.6. Any Lagrangian representation 
$\boldsymbol{\eta}$ of 
$(1,\boldsymbol{b})$ is concentrated on 
$\Gamma_{\boldsymbol{b}}$.
Proof. Let 
$\boldsymbol{\eta}$ be a Lagrangian representation of 
$(1,\boldsymbol{b})$. Let 
$D$ be a countable dense subset of 
$[0,1]$. Let 
$\phi\in C_c^\infty((0,1)\times (0,1)^d)$ be a standard mollifier. Define
\begin{equation*}\phi^\varepsilon(t,x):=\frac{1}{{\varepsilon^{d+1}}}\phi(\frac{t}{\varepsilon},\frac{x}{\varepsilon}),\end{equation*} and denote 
$\boldsymbol{b}^\varepsilon=\boldsymbol{b}\ast \phi^\varepsilon$. Let 
$s,t\in D$. Notice that for every 
$\varepsilon \gt 0$, we have
\begin{equation}
\begin{aligned}
&\int_\Gamma\Big|\gamma(t)-\gamma(s)-\int_s^t\boldsymbol{b}^\varepsilon(\tau,\gamma(\tau))d\tau\Big|\boldsymbol{\eta}(d\gamma)\\
&\quad \leq \int_\Gamma\Big|\gamma(t)-\gamma(s)\Big|\boldsymbol{\eta}(d\gamma)+\int_\Gamma\int_s^t|\boldsymbol{b}^\varepsilon(\tau,\gamma(\tau))d\tau|\boldsymbol{\eta}(d\gamma)\\
&\quad \leq\int_\Gamma\int_s^t|\boldsymbol{b}(\tau,\gamma(\tau))|d\tau\boldsymbol{\eta}(d\gamma)+\int_\Gamma\int_s^t|\boldsymbol{b}^\varepsilon(\tau,\gamma(\tau))|d\tau\boldsymbol{\eta}(d\gamma)\\
&\quad =\int_s^t\int_{\mathbb{T}^d} |\boldsymbol{b}(\tau,x)|dxd\tau + \int_s^t\int_{\mathbb{T}^d} |\boldsymbol{b}^\varepsilon(\tau,x)|dxd\tau \\
&\quad \leq 2|t-s|\|\boldsymbol{b}\|_{L^\infty_{t,x}},
\end{aligned}
\end{equation} where in the second to last line, we have used Fubini, as well as 
$(e_\tau)_\#\boldsymbol{\eta} = \mathscr{L}^{d}$, and in the last line we have used that 
$\|\boldsymbol{b}^\varepsilon\|_{L^\infty_{t,x}}\leq \|\boldsymbol{b}\|_{L^\infty_{t,x}}$ and Hölder’s inequality. Therefore, by the dominated convergence theorem, it holds that
\begin{equation}
\int_\Gamma\Big|\gamma(t)-\gamma(s)-\lim_{\varepsilon\downarrow 0}\int_s^t\boldsymbol{b}^\varepsilon(\tau,\gamma(\tau))d\tau\Big|\boldsymbol{\eta}(d\gamma)=0,
\end{equation} which implies that there exists a set 
$N_{s,t}\subset\Gamma$ of vanishing 
$\boldsymbol{\eta}$ measure such that for every 
$\gamma\in\Gamma-N_{s,t}$, we have
\begin{equation}
\gamma(t)-\gamma(s)=\lim_{\varepsilon\downarrow 0}\int_s^t\boldsymbol{b}^\varepsilon(\tau,\gamma(\tau))d\tau.
\end{equation} Since 
$\|\boldsymbol{b}^\varepsilon\|_{L^\infty_{t,x}}\leq \|\boldsymbol{b}\|_{L^\infty_{t,x}}$, it therefore holds that for every 
$\gamma\in\Gamma-N_{s,t}$
\begin{equation}
|\gamma(t)-\gamma(s)|\leq |t-s|\|\boldsymbol{b}\|_{L^\infty_{t,x}}.
\end{equation}Define
\begin{equation*}N:=\bigcup_{s,t\in D} N_{s,t},\end{equation*} which is a set of vanishing 
$\boldsymbol{\eta}$ measure since 
$D$ is countable. As 
$s,t$ were arbitrary in 
$D$, and by density of 
$D$ in 
$[0,1]$, we therefore have that for every 
$\gamma\in \Gamma-N$, it holds
\begin{equation*}
|\gamma(t)-\gamma(s)|\leq |t-s|\|\boldsymbol{b}\|_{L^\infty_{t,x}} \qquad\forall s,t\in[0,1].
\end{equation*}This proves the thesis.
Next we present our main tool: the disintegration of a measure with respect to a Borel map and a target measure. In the study of weak solutions of the continuity equation, disintegration has previously been used in [Reference Alberti, Bianchini and Crippa1] by Alberti, Bianchini and Crippa to establish the optimal uniqueness result for the continuity equation along a bounded, divergence-free, and autonomous vector field in the two-dimensional setting. In [Reference Bianchini and Bonicatto5], Bianchini and Bonicatto also used disintegration to prove a uniqueness result for nearly incompressible vector fields in 
$L^1_tBV_x$. In view of Lemma 1.6, we will identify a Lagrangian representation of 
$(1,\boldsymbol{b})$ with its restriction to the Borel 
$\sigma$-algebra of the compact set 
$\Gamma_{\boldsymbol{b}}$, and thanks to Remark 1.5, we will be able to perform a disintegration of this measure.
1.2. Disintegration of measures
Let 
$X$ and 
$Y$ be compact, separable metric spaces, 
${\boldsymbol{\mu}}$ a positive measure on 
$X$, 
$f:X\to Y$ a Borel map, 
${\boldsymbol{\nu}}$ a positive measure on 
$Y$ such that 
$f_\#{\boldsymbol{\mu}} \ll {\boldsymbol{\nu}}$. Then there exists a Borel family 
$\{{\boldsymbol{\mu}}_y : y\in Y\}$ of measures on 
$X$ such that
(1)
${\boldsymbol{\mu}}_y$ is supported on the level set
$E_y:=f^{-1}(y)$ for every
$y\in Y$;(2) the measure
${\boldsymbol{\mu}}$ can be decomposed as
${\boldsymbol{\mu}}=\int_Y{\boldsymbol{\mu}}_yd{\boldsymbol{\nu}}(y)$, which means that
(1.9)\begin{equation}
{\boldsymbol{\mu}}(A)=\int_Y{\boldsymbol{\mu}}_y(A)d{\boldsymbol{\nu}}(y)
\end{equation}for every Borel set
$A$ contained in
$X$.
If we further assume that 
$f_\#{\boldsymbol{\mu}}={\boldsymbol{\nu}}$, then there exists a Borel family 
$\{{\boldsymbol{\mu}}_y : y\in Y\}$ of probability measures on 
$X$ satisfying 
$(i)$ and 
$(ii)$.
Any family satisfying 
$(i)$ and 
$(ii)$ is called a disintegration of 
${\boldsymbol{\mu}}$ with respect to 
$f$ and 
${\boldsymbol{\nu}}$. The disintegration is essentially unique in the following sense: for any other disintegration 
$\{\tilde{{\boldsymbol{\mu}}}_y:y\in Y\}$ there holds 
${\boldsymbol{\mu}}_y=\tilde{\boldsymbol{\mu}}_y$ for 
${\boldsymbol{\nu}}$-a.e. 
$y\in Y$. The above facts are cited from [Reference Alberti, Bianchini and Crippa1], and are proven in Dellacherie and Meyer [Reference Dellacherie and Meyer7].
We now give a useful fact. Let 
$g:X\to X$ a Borel map such that:
(P) for every
$y\in Y$, we have
$g^{-1}((f^{-1}(y))^c)=(f^{-1}(y))^c$.
The following is true.
Lemma 1.7. In the context of this paragraph, if 
$\{{\boldsymbol{\mu}}_y : y\in Y\}$ is a disintegration of 
${\boldsymbol{\mu}}$ with respect to 
$ f$ and 
${\boldsymbol{\nu}}$, then 
$\{g_\# {\boldsymbol{\mu}}_y : y\in Y\}$ is a disintegration of 
$g_\#{\boldsymbol{\mu}}$ with respect to 
$ f $ and 
${\boldsymbol{\nu}}$.
Proof. Let 
$y\in Y$. Observe that 
$g_\#{\boldsymbol{\mu}}_y((f^{-1}(y))^c)=\mu_y(g^{-1}(f^{-1}(y))^c)=\mu_y((f^{-1}(y))^c)=0$ where we have used (P) in the second to last equality and that 
${\boldsymbol{\mu}}_y$ is concentrated on 
$f^{-1}(y)$ in the last equality. So 
$g_\#{\boldsymbol{\mu}}_y$ is supported on 
$f^{-1}(y)$, and since 
$y$ was arbitrary, this proves 
$(i)$.
Let 
$A$ a Borel set in 
$X$. Then, as 
$g^{-1}(A)$ is a Borel set in 
$X$, it follows that
\begin{equation}
g_\#{\boldsymbol{\mu}}(A)={\boldsymbol{\mu}}(g^{-1}(A))=\int_Y {\boldsymbol{\mu}}_y (g^{-1}(A))d{\boldsymbol{\nu}}(y)=\int_Y g_\#{\boldsymbol{\mu}}_y (A)d{\boldsymbol{\nu}}(y),
\end{equation} which gives 
$(ii)$.
We also have the following property of the disintegration, which we will use in this paper:
\begin{equation}
\int_X \phi d{\boldsymbol{\mu}}=\int_Y\Big[\int_{E_y}\phi d{\boldsymbol{\mu}}_y\Big]d{\boldsymbol{\nu}}(y),
\end{equation} for every Borel function 
$\phi:X\to [0,+\infty]$.
1.3. Uniqueness of regular measurable selection
Ambrosio [Reference Ambrosio2] proved the existence and essential uniqueness of regular measurable selections in the bounded variation setting, thereby extending the work of DiPerna and Lions [Reference DiPerna and Lions9]. The following can be extracted from Ambrosio [Reference Ambrosio2].
Theorem 1.8 Consider a divergence-free vector field 
$\boldsymbol{b}\in L^1((0,1);BV(\mathbb{T}^d;\mathbb{R}^d))$. Then for every 
$s\in[0,1]$, there exists an essentially unique regular measurable selection 
$\{\gamma_{s,x}\}$ of integral curves of 
$\boldsymbol{b}$ such that for every 
$\rho \in C([0,1];w^*-L^\infty (\mathbb{T}^d))$ for which 
$\rho(1,\boldsymbol{b})$ solves (PDE), the unique Lagrangian representation 
$\boldsymbol{\eta}$ of 
$\rho(1,\boldsymbol{b})$ satisfies
\begin{equation}
\boldsymbol{\eta}=\int_{\mathbb{T}^d}{{\boldsymbol{\delta}}}_{\gamma_{s,x}}\rho(s,x)dx.
\end{equation} The above theorem implies that, if two bounded vector fields 
$\rho(1,\boldsymbol{b})$ and 
$\tilde\rho(1,\boldsymbol{b})$ solve (PDE) and satisfy 
$\rho(s,x)=\tilde\rho(s,x)$ for 
$\mathscr{L}^{d}$-a.e. 
$x\in \mathbb{T}^d$, then 
$\rho=\tilde\rho$, which is the uniqueness result of Ambrosio for the Cauchy problem for the continuity equation with a vector field in 
$L^1_tBV_x$.
Given 
$\tau \gt 0,$ we define the truncated versions of 
$\boldsymbol{b}$
\begin{equation}
\boldsymbol{b}^\tau(t,x):=\left\{
\begin{aligned}
\boldsymbol{b}(t,x)\qquad &\text{if} \quad t\geq \tau,\\
0\qquad &\text{if}\quad t \lt \tau.
\end{aligned}
\right.
\end{equation} Given two positive real numbers 
$a$ and 
$b$, we will write 
$a\vee b =\max\{a,b\}.$ Under the assumption that the bounded variation norm of 
$\boldsymbol{b}$ is not integrable at time zero, the following essential uniqueness of regular measurable selections of integral curves still holds.
Proposition 1.9. Let 
$s\in(0,1]$. Assume that 
$\boldsymbol{b}$ belongs to 
$L_{loc}^1((0,1];BV(\mathbb{T}^d;\mathbb{R}^d)),$ and consider two regular measurable selections 
$\{\gamma^1_{s,x}\}$ and 
$\{\gamma^2_{s,x}\}$ of integral curves of 
$\boldsymbol{b}$ starting from 
$s$. Then 
$\gamma^1_{s,x}=\gamma^2_{s,x}$ for 
$\mathscr{L}^{d}$-a.e. 
$x\in\mathbb{T}^d.$
Proof. Let 
$k\in\mathbb{N}$. It can be verified directly that the two measurable selections 
$\{\gamma^1_{s,x}(1/k\vee \cdot)\}$ and 
$\{\gamma^2_{s,x}(1/k\vee \cdot)\}$ are regular measurable selections of integral curves of the vector field 
$\boldsymbol{b}^{1/k}$ defined in (1.13). Note that this vector field belongs to 
$L^1((0,1);BV(\mathbb{T}^d;\mathbb{R}^d))$, so in view of Theorem 1.8, we have 
$\gamma_{s,x}^1(1/k\vee\cdot)=\gamma^2_{s,x}(1/k\vee \cdot)$ for every 
$x\in \mathbb{T}^d-N_k$, where 
$N_k$ is a set of vanishing Lebesgue measure. Define
\begin{equation*}N:=\bigcup_{k\in\mathbb{N}} N_k,\end{equation*} which is of vanishing Lebesgue measure. Then, for every 
$k\in\mathbb{N}$, we have 
$\gamma_{s,x}^1(1/k\vee\cdot)=\gamma^2_{s,x}(1/k\vee \cdot)$ for every 
$x\in \mathbb{T}^d-N,$ which implies 
$\gamma_{s,x}^1=\gamma^2_{s,x}$ for every 
$x\in \mathbb{T}^d-N$ by continuity. The thesis follows.
1.4. Statement of results
In this paper, the vector field 
$\boldsymbol{b}$ will satisfy the hypothesis of Proposition 1.9. Accordingly, we fix for the rest of the paper 
$\{\gamma_{1,y}\}$ a (essentially unique) regular measurable selection of integral curves of 
$\boldsymbol{b}$ starting from time 
$1$. 
$\boldsymbol{b}_{DP}$ denotes the bounded, divergence-free vector field in 
$L_{loc}^1((0,1];BV(\mathbb{T}^2;\mathbb{R}^2))$ constructed by Depauw in [Reference Depauw8]. For completeness we give a construction of 
$\boldsymbol{b}_{DP}$ in the Appendix. We now state our main theorem.
Theorem 1.10 Consider a bounded, divergence-free vector field 
$\boldsymbol{b}:[0,1]\times\mathbb{T}^d\to\mathbb{R}^d$. Assume that 
$\boldsymbol{b}\in L_{loc}^1((0,1];BV(\mathbb{T}^d;\mathbb{R}^d))$. Then there exists a unique Lagrangian representation 
$\boldsymbol{\eta}$ of 
$(1,\boldsymbol{b})$, which furthermore has the following properties:
(i) the family of probability measures
$\{{{\boldsymbol{\delta}}}_{\gamma_{1,y}}\}$ is a disintegration of
$\boldsymbol{\eta}$ with respect to
$e_1$ and
$\mathscr{L}^{d}$;(ii) for every smooth sequence
$(\boldsymbol{b}^k)_{k\in\mathbb{N}}$ such that
$\boldsymbol{b}^k\rightarrow \boldsymbol{b}$ in
$L^1_{loc}$,
$\|\boldsymbol{b}^k\|_{L^\infty_{t,x}}\leq \|\boldsymbol{b}\|_{L^\infty_{t,x}}$, and
$\operatorname{div}_x\boldsymbol{b}^k=0$, the unique Lagrangian representation of
$(1,\boldsymbol{b}^k)$ converges narrowly to
$\boldsymbol{\eta}$ as
$k\to+\infty$;(iii) there exists a Borel family of probability measures
$\{\tilde{\boldsymbol{\nu}}_x\}$ on
$\mathbb{T}^d$ such that any disintegration
$\{\boldsymbol{\eta}_{0,x}\}$ of
$\boldsymbol{\eta}$ with respect to
$e_0$ and
$\mathscr{L}^{d}$ satisfies
(1.14)\begin{equation}
\boldsymbol{\eta}_{0,x}=\int_{\mathbb{T}^d}{{\boldsymbol{\delta}}}_{\gamma_{1,y}}\tilde{\boldsymbol{\nu}}_x(dy),
\end{equation}for
$\mathscr{L}^{d}$-a.e.
$x\in\mathbb{T}^d$.Moreover, for the vector field
$\boldsymbol{b}=\boldsymbol{b}_{DP}$, the measure
$\tilde{\boldsymbol{\nu}}_x$ is not a Dirac mass for
$\mathscr{L}^{2}$-a.e.
$x\in\mathbb{T}^2$.
Observe that a sequence satisfying the hypothesis of 
$(ii)$ can be generated by regularising 
$\boldsymbol{b}$ by convolution. We further ask the following question on the measures 
$\tilde{\boldsymbol{\nu}}_x$ of the above theorem, which capture the stochastic behaviour of the Lagrangian representation 
$\boldsymbol{\eta}$.
Question. Can one construct a bounded, divergence-free vector field in 
$L^1_{loc}((0,1];BV(\mathbb{T}^d;\mathbb{R}^d))$ such that the measures 
$\tilde{\boldsymbol{\nu}}_x$ are absolutely continuous with respect to 
$\mathscr{L}^{d}$ for 
$\mathscr{L}^{d}$-a.e. 
$x\in\mathbb{T}^d$?
We finally note that the class of vector field under study in this article has been previously investigated in [Reference Ambrosio, Crippa, Figalli and Spinolo4] and that stochastic selection has been investigated for a toy model in [Reference Mailybaev and Raibekas10].
1.5. Plan of the paper
In 
$\S$ 2, we prove that there exists a unique Lagrangian representation of 
$(1,\boldsymbol{b})$ under the hypothesis of Theorem 1.10, as well as 
$(i)$ and 
$(ii)$ of Theorem 1.10. In 
$\S$ 3, we prove 
$(iii)$ of Theorem 1.10. In the Appendix, we give for completeness a construction of 
$\boldsymbol{b}_{DP}$, the vector field constructed by Depauw in [Reference Depauw8].
2. Uniqueness of the Lagrangian representation
In this section, 
$\boldsymbol{b}:[0,1]\times\mathbb{T}^d\to\mathbb{R}^d$ is an essentially bounded, divergence-free Borel vector field satisfying the assumptions of Theorem 1.10, namely 
$\boldsymbol{b}\in L^1_{loc}((0,1];BV(\mathbb{T}^d;\mathbb{R}^d))$.
2.1. Backwards stopping of the Lagrangian representation
Let 
$\boldsymbol{\eta}$ be a Lagrangian representation of 
$(1,\boldsymbol{b})$, which exists by Theorem 1.4, and let 
$ \{\boldsymbol{\eta}_{1,y}\}$ be a disintegration with respect to 
$e_1$ and 
$\mathscr{L}^{d}$. Let 
$\{\gamma_{1,y}\}$ be a (essentially unique) regular measurable selection of integral curves of 
$\boldsymbol{b}$. Our goal is now to prove that for 
$\mathscr{L}^{d}$-a.e. 
$y\in\mathbb{T}^d$, we have
\begin{equation}
\boldsymbol{\eta}_{1,y}={{\boldsymbol{\delta}}}_{\gamma_{1,y}},
\end{equation}which will imply by definition of the disintegration that
\begin{equation*}\boldsymbol{\eta}=\int_{\mathbb{T}^d}{{\boldsymbol{\delta}}}_{\gamma_{1,y}}dy,\end{equation*} from which uniqueness of the Lagrangian representation of 
$(1,\boldsymbol{b}),$ as well as part 
$(i)$ of Theorem 1.10 will follow. Let 
$\tau \gt 0$ and consider the backward stopping map
\begin{equation*}S^\tau :\Gamma_{\boldsymbol{b}} \ni \gamma(\cdot) \longmapsto \gamma( \tau \vee\cdot)\in\Gamma_{\boldsymbol{b}}.\end{equation*} Note that 
$S^\tau$ clearly satisfies (P) of 
$\S$ 1.2 with 
$X= \Gamma_{\boldsymbol{b}}$, 
$Y=\mathbb{T}^d$, 
$f=e_1$, and 
$g=S^\tau$. Therefore, by Lemma 1.7, 
$ \{(S^\tau)_\#\boldsymbol{\eta}_{1,y}\}$ is a disintegration of 
$(S^\tau)_\#\boldsymbol{\eta}$ with respect to 
$e_1$ and 
$\mathscr{L}^{d}$. For simplicity, we will write 
$\boldsymbol{\eta}^\tau:=(S^\tau)_\#\boldsymbol{\eta}$ and 
$\boldsymbol{\eta}_{1,y}^\tau:=(S^\tau)_\#\boldsymbol{\eta}_{1,y}$. Recall that we have defined in (1.13) the truncated version 
$\boldsymbol{b}^\tau$ of 
$\boldsymbol{b}$. We then have the following lemma.
Lemma 2.1. For every 
$\tau \gt 0$, the family 
$\{{{\boldsymbol{\delta}}}_{\gamma_{1,y}(\tau\vee\cdot)}\}$ is a disintegration of 
$\boldsymbol{\eta}^\tau$ with respect to 
$e_1$ and 
$\mathscr{L}^{d}$.
Proof. As 
$\boldsymbol{b}^\tau$ belongs to 
$L^1((0,1);BV(\mathbb{T}^d;\mathbb{R}^d))$ is bounded, and divergence-free, there is an essentially unique regular measurable selection 
$\{\gamma^\tau_{1,y}\}$ of integral curves of 
$\boldsymbol{b}^\tau$ thanks to Theorem 1.8. Now, observe that 
$\{\gamma_{1,y}(\tau\vee \cdot)\}$ is a regular measurable selection of integral curves of 
$\boldsymbol{b}^\tau$, hence for 
$\mathscr{L}^{d}$-a.e. 
$y\in\mathbb{T}^d$, we have that 
$\gamma^\tau_{1,y}( \cdot)=\gamma_{1,y}(\tau\vee\cdot)$. It can be checked directly that 
$\boldsymbol{\eta}^\tau$ is a Lagrangian representation of 
$(1,\boldsymbol{b}^\tau)$. So by Theorem 1.8, 
$\{{{\boldsymbol{\delta}}}_{\gamma^\tau_{1,y}}\}$ is a disintegration of 
$\boldsymbol{\eta}^\tau$ with respect to 
$e_1$ and 
$\mathscr{L}^{d}$ so that
\begin{equation*}
\boldsymbol{\eta}^\tau=\int_{\mathbb{T}^d}{{\boldsymbol{\delta}}}_{\gamma^\tau_{1,y}}dy.
\end{equation*} Therefore, by essential uniqueness of the disintegration, 
$\{{{\boldsymbol{\delta}}}_{\gamma_{1,y}(\tau\vee \cdot)}\}$ is a disintegration of 
$\boldsymbol{\eta}^\tau$ with respect to 
$e_1$ and 
$\mathscr{L}^{d}$ so that
\begin{equation*}
\boldsymbol{\eta}^\tau=\int_{\mathbb{T}^d}{{\boldsymbol{\delta}}}_{\gamma_{1,y}(\tau\vee \cdot)}dy.
\end{equation*}We also have the following simple fact.
Lemma 2.2. Let 
${\boldsymbol{\mu}}$ be a probability measure on 
$\Gamma_{\boldsymbol{b}}$. Then 
$(S^\tau)_\#{\boldsymbol{\mu}}$ converges narrowly to 
${\boldsymbol{\mu}}$ as 
$\tau\downarrow 0$.
Proof. Let 
$\Phi \in C_c(\Gamma_{\boldsymbol{b}})$. For every 
$\gamma\in \Gamma_{\boldsymbol{b}}$, we have 
$\lim_{\tau\downarrow0} S^\tau\gamma=\gamma$. Then we have 
$\lim_{\tau\downarrow 0}\Phi(S^\tau\gamma)=\Phi(\gamma)$ by continuity of 
$\Phi$. Also, we clearly have
\begin{equation*}
{ | \Phi(S^\tau\gamma)|\leq \|\Phi\|_{C^0} \qquad\forall \tau \gt 0.}
\end{equation*}So, by dominated convergence, it holds that
\begin{equation*}
\lim_{\tau\downarrow 0} \int_{\Gamma_{\boldsymbol{b}}} \Phi(\gamma)(S^\tau)_\#{\boldsymbol{\mu}}(d\gamma)= \lim_{\tau\downarrow 0} \int_{\Gamma_{\boldsymbol{b}}} \Phi(S^\tau\gamma){\boldsymbol{\mu}}(d\gamma)=\int_{\Gamma_{\boldsymbol{b}}} \Phi(\gamma){\boldsymbol{\mu}}(d\gamma).
\end{equation*} Since 
$\Phi$ was arbitrary in 
$C_c(\Gamma_{\boldsymbol{b}})$, the thesis follows.
2.2. Proof of
$(i)$ of Theorem 1.10
Proof. Recall that 
$\boldsymbol{\eta}$ is a Lagrangian representation of 
$(1,\boldsymbol{b})$, which in view of Lemma 1.6 is a probability measure on 
$\Gamma_{\boldsymbol{b}}$. Recall also that 
$\{\boldsymbol{\eta}_{1,y}\}$ is a disintegration of 
$\boldsymbol{\eta}$ with respect to 
$e_1$ and 
$\mathscr{L}^{d}$. Recall also that 
$\{\gamma_{1,y}\}$ is a (essentially unique) regular measurable selection of integral curves of 
$\boldsymbol{b}$. Let us prove (2.1), which will yield both uniqueness of the Lagrangian representation of 
$(1,\boldsymbol{b})$ as well as 
$(i)$ of Theorem 1.10, namely it will show
\begin{equation}
\boldsymbol{\eta}=\int_{\mathbb{T}^d}{{\boldsymbol{\delta}}}_{\gamma_{1,y}}dy.
\end{equation} By separability, there exists a countable subset 
$\mathcal{N}$ of 
$C_c({\Gamma_{\boldsymbol{b}}})$, which is dense. Let 
$\tau \gt 0,$ and let 
$\{\boldsymbol{\eta}_{1,y}\}$ be a disintegration of 
$\boldsymbol{\eta}$ with respect to 
$e_1$ and 
$\mathscr{L}^{d}$. By Lemma 1.7, 
$\{\boldsymbol{\eta}_{1,y}^\tau\}$ is a disintegration of 
$\boldsymbol{\eta}^\tau$ with respect to 
$e_1$ and 
$\mathscr{L}^{d}$. By Lemma 2.1, and by essential uniqueness of the disintegration, we have 
${{\boldsymbol{\delta}}}_{\gamma_{1,y}(\tau\vee\cdot)}=\boldsymbol{\eta}_{1,y}^\tau$ for 
$\mathscr{L}^{d}$-a.e. 
$y\in \mathbb{T}^d$. Let 
$\Phi\in \mathcal{N}$, and let 
$B$ be a Borel set in 
$\mathbb{T}^d$. We then have that
\begin{equation}
\begin{aligned}
\int_B \int_{\Gamma_{\boldsymbol{b}}} \Phi(\gamma){{\boldsymbol{\delta}}}_{\gamma_{1,y}}(d\gamma)dy&=\int_{B}\lim_{\tau\downarrow 0}\int_{\Gamma_{\boldsymbol{b}}} \Phi(\gamma){{\boldsymbol{\delta}}}_{\gamma_{1,y}(\tau\vee \cdot)}(d\gamma)dy\\
&=\int_{B}\lim_{\tau\downarrow 0}\int_{\Gamma_{\boldsymbol{b}}} \Phi(\gamma)\boldsymbol{\eta}^{\tau}_{1,y}(d\gamma)dy\\
&=\int_{B}\int_{\Gamma_{\boldsymbol{b}}}\Phi(\gamma)\boldsymbol{\eta}_{1,y}(d\gamma)dy,
\end{aligned}
\end{equation} where in the first equality, we have used that 
${{\boldsymbol{\delta}}}_{\gamma_{1,y}(\tau\vee \cdot)}$ converges narrowly to 
${{\boldsymbol{\delta}}}_{\gamma_{1,y}}$ as 
$\tau\downarrow 0$ by Lemma 2.2. In the second to last equality, we have used that 
${{\boldsymbol{\delta}}}_{\gamma_{1,y}(\tau\vee\cdot)}=\boldsymbol{\eta}_{1,y}^\tau$ for 
$\mathscr{L}^{d}$-a.e. 
$y\in \mathbb{T}^d$, which follows from Lemma 2.1. In the last equality, we have used Lemma 2.2. As 
$B$ was an arbitrary Borel set of 
$\mathbb{T}^d$, we have that there exists a set 
$N_\Phi$ of vanishing Lebesgue measure such that for every 
$y\in \mathbb{T}^d-N_\Phi$, we have
\begin{equation*}\int_{\Gamma_{\boldsymbol{b}}} \Phi(\gamma){{\boldsymbol{\delta}}}_{\gamma_{1,y}}(d\gamma)=\int_{\Gamma_{\boldsymbol{b}}} \Phi(\gamma)\boldsymbol{\eta}_{1,y}(d\gamma).\end{equation*}Now, let
\begin{equation*}N:=\bigcup_{\Phi\in \mathcal{N}}N_\Phi.\end{equation*} It is a set of vanishing Lebesgue measure as 
$\mathcal{N}$ is countable, and for every 
$y\in \mathbb{T}^d-N$, we have
\begin{equation*}\int_{\Gamma_{\boldsymbol{b}}} \Phi(\gamma){{\boldsymbol{\delta}}}_{\gamma_{1,y}}(d\gamma)=\int_{\Gamma_{\boldsymbol{b}}} \Phi(\gamma)\boldsymbol{\eta}_{1,y}(d\gamma) \qquad\forall \Phi\in \mathcal{N}.\end{equation*} By density of 
$\mathcal{N}$ in 
$C_c(\Gamma_{\boldsymbol{b}})$, for every 
$y\in \mathbb{T}^d-N$, we have
\begin{equation*}\int_{\Gamma_{\boldsymbol{b}}} \Phi(\gamma){{\boldsymbol{\delta}}}_{\gamma_{1,y}}(d\gamma)=\int_{\Gamma_{\boldsymbol{b}}} \Phi(\gamma)\boldsymbol{\eta}_{1,y}(d\gamma) \qquad\forall \Phi\in C_c(\Gamma_{\boldsymbol{b}}).\end{equation*} This proves that for 
$\mathscr{L}^{d}$-a.e. 
$y\in \mathbb{T}^d$, we have 
$\boldsymbol{\eta}_{1,y}={{\boldsymbol{\delta}}}_{\gamma_{1,y}}$, which proves (2.2). As 
$\boldsymbol{\eta}$ was an arbitrary Lagrangian representation of 
$(1,\boldsymbol{b})$, this proves both that there exists a unique Lagrangian representation of 
$(1,\boldsymbol{b})$, and 
$(i)$ of Theorem 1.10.
We will now prove that the unique Lagrangian representation of 
$(1,\boldsymbol{b})$ can be obtained as the unique limit of Lagrangian representations of suitable regularisations of 
$(1,\boldsymbol{b})$.
2.3. Proof of
$(ii)$ of Theorem 1.10
Proof. Let 
$(\boldsymbol{b}^k)_{k\in\mathbb{N}}$ be a smooth sequence such that 
$\boldsymbol{b}^k\to\boldsymbol{b}$ in 
$L^1_{loc}$ and such that, for every 
$k\in\mathbb{N}$, we have
\begin{equation}
\sup_{(t,x)\in [0,1]\times \mathbb{T}^d} |\boldsymbol{b}^k(t,x)|\leq \|\boldsymbol{b}\|_{L^\infty_{t,x}},
\end{equation} and such that 
$\operatorname{div}_x\boldsymbol{b}^k=0$. Let 
${{\boldsymbol{X}}}^k:[0,1]\times \mathbb{T}^d\to\mathbb{T}^d$ be the unique flow along 
$\boldsymbol{b}^k$, namely 
${{\boldsymbol{X}}}^k$ solves
\begin{equation}
\left\{
\begin{aligned}
\partial_t {{\boldsymbol{X}}}^k(t,x)&=\boldsymbol{b}^k({{\boldsymbol{X}}}^k(t,x)),\\
{{\boldsymbol{X}}}^k(0,x)&=x.
\end{aligned}
\right.
\end{equation}The measure defined by
\begin{equation*}\boldsymbol{\eta}^k(A)=\int_{\mathbb{T}^d}{{\boldsymbol{\delta}}}_{{{\boldsymbol{X}}}^k(\cdot,x)}(A)dx,\end{equation*} for every Borel set 
$A$ in 
$\Gamma$ is then the unique Lagrangian representation of 
$(1,\boldsymbol{b}^k)$, as we clearly have 
$(e_t)_\#\boldsymbol{\eta}^k={{\boldsymbol{X}}}^k(t,\cdot)_\#\mathscr{L}^{d}=\mathscr{L}^{d},$ since 
$\boldsymbol{b}^k$ is divergence-free, and also that 
$\boldsymbol{\eta}^k$ is clearly concentrated on integral curves of 
$\boldsymbol{b}^k$.
Step 1. Compactness. Recall that 
$\Gamma_{\boldsymbol{b}}$ is the space Lipchitz paths with Lipschitz constant 
$\|\boldsymbol{b}\|_{L^\infty_{t,x}}$ defined in (1.4). In view of Lemma 1.6, we have that 
$\boldsymbol{\eta}^k(\Gamma_{\boldsymbol{b}})=1$ for every 
$k\in\mathbb{N}$. As 
$\Gamma_{\boldsymbol{b}}$ is compact by Remark 1.5, it follows by Prokhorov theorem, that there exists an increasing map 
$\xi :\mathbb{N}\to\mathbb{N}$ such that 
$\boldsymbol{\eta}^{\xi(k)}$ converges narrowly to some probability measure 
$\boldsymbol{\eta}$ on 
$\Gamma_{\boldsymbol{b}}$ as 
$k\to+\infty.$
Step 2. Let us prove that 
$\boldsymbol{\eta}$ is a Lagrangian representation of 
$(1,\boldsymbol{b})$. Let 
$\phi\in C(\mathbb{T}^d)$ and 
$t\in [0,1]$. We have that 
$\Gamma_{\boldsymbol{b}}\ni \gamma \longmapsto \phi(e_t(\gamma))$ is in 
$C_c(\Gamma_{\boldsymbol{b}})$. Therefore,
\begin{equation*}
\int_{\Gamma_{\boldsymbol{b}}} \phi(e_t(\gamma))\boldsymbol{\eta}(d\gamma)=\lim_{k\to+\infty}\int_{\Gamma_{\boldsymbol{b}}} \phi(e_t(\gamma))\boldsymbol{\eta}^{\xi(k)}(d\gamma)=\int_{\mathbb{T}^d}\phi(x)dx.
\end{equation*} As 
$\phi$ and 
$t$ were arbitrary, this implies that 
$(e_t)_\#\boldsymbol{\eta}=\mathscr{L}^{d}$ for every 
$t\in[0,1]$. We still need to prove that 
$\boldsymbol{\eta}$ is concentrated on integral curves of 
$\boldsymbol{b}.$ Let 
$s,t\in[0,1]$. We have to check that
\begin{equation}
\int_{\Gamma_{\boldsymbol{b}}} \Big|\gamma(t)-\gamma(s)-\int_s^t\boldsymbol{b}(\tau,\gamma(\tau))d\tau\Big|\boldsymbol{\eta}(d\gamma)=0.
\end{equation}We know that
\begin{equation*}
\int_{\Gamma_{\boldsymbol{b}}} \Big|\gamma(t)-\gamma(s)-\int_s^t\boldsymbol{b}(\tau,\gamma(\tau))d\tau\Big|\boldsymbol{\eta}^{\xi(k)}(d\gamma)=0,
\end{equation*} however we cannot pass into the limit 
$k\to +\infty$ in the above equation because the functional
\begin{equation}
\Gamma_{\boldsymbol{b}} \ni \gamma \longmapsto \Big|\gamma(t)-\gamma(s)-\int_s^t\boldsymbol{b}(\tau,\gamma(\tau))d\tau\Big|\in\mathbb{R},
\end{equation} need not be continuous since 
$\boldsymbol{b}$ is not continuous. To circumvent this problem, let 
$\varepsilon \gt 0$ and let 
${{\boldsymbol{c}}}:[0,1]\times \mathbb{T}^d\to \mathbb{R}^d$ be a continuous vector field such that 
$\int_s^t|{{\boldsymbol{c}}}(\tau,x)-\boldsymbol{b}(\tau,x)|d\tau dx \lt \varepsilon$. We then have
\begin{equation*}
\begin{aligned}
&\int_{\Gamma_{\boldsymbol{b}}} \Big|\gamma(t)-\gamma(s)-\int_s^t\boldsymbol{b}(\tau,\gamma(\tau))d\tau\Big|\boldsymbol{\eta}(d\gamma)\\
&\overset{1}{\leq} \int_{\Gamma_{\boldsymbol{b}}}\Big|\gamma(t)-\gamma(s)-\int_s^t{{\boldsymbol{c}}}(\tau,\gamma(\tau))d\tau\Big|\boldsymbol{\eta}(d\gamma)+\int_{\Gamma_{\boldsymbol{b}}} \Big|\int_s^t{{\boldsymbol{c}}}(\tau,\gamma(\tau))-\boldsymbol{b}(\tau,\gamma(\tau))\Big|\boldsymbol{\eta}(d\gamma)\\
&\overset{2}{\leq} \limsup_{k\to +\infty} \int_{\Gamma_{\boldsymbol{b}}}\Big|\gamma(t)-\gamma(s)-\int_s^t{{\boldsymbol{c}}}(\tau,\gamma(\tau))d\tau\Big|\boldsymbol{\eta}^k(d\gamma) \\
&\quad +\int_{\Gamma_{\boldsymbol{b}}} \Big|\int_s^t{{\boldsymbol{c}}}(\tau,\gamma(\tau))-\boldsymbol{b}(\tau,\gamma(\tau))\Big|\boldsymbol{\eta}(d\gamma)\\
&\overset{3}{=} \limsup_{k\to +\infty} \int_{\Gamma_{\boldsymbol{b}}}\Big|\int_s^t(\boldsymbol{b}^k(\tau,\gamma(\tau))-{{\boldsymbol{c}}}(\tau,\gamma(\tau)))d\tau\Big|\boldsymbol{\eta}^k(d\gamma) \\
&\quad +\int_{\Gamma_{\boldsymbol{b}}} \Big|\int_s^t({{\boldsymbol{c}}}(\tau,\gamma(\tau))-\boldsymbol{b}(\tau,\gamma(\tau)))d\tau\Big|\boldsymbol{\eta}(d\gamma)\\
&\overset{4}{\leq} \limsup_{k\to +\infty} \int_{\Gamma_{\boldsymbol{b}}}\int_s^t\Big|\boldsymbol{b}^k(\tau,\gamma(\tau))-{{\boldsymbol{c}}}(\tau,\gamma(\tau))\Big|d\tau\boldsymbol{\eta}^k(d\gamma) \\
&\quad +\int_{\Gamma_{\boldsymbol{b}}} \int_s^t\Big|{{\boldsymbol{c}}}(\tau,\gamma(\tau))-\boldsymbol{b}(\tau,\gamma(\tau))\Big|d\tau\boldsymbol{\eta}(d\gamma)\\
&\overset{5}{=} \limsup_{k\to +\infty} \int_{\Gamma_{\boldsymbol{b}}}\int_s^t\Big|\boldsymbol{b}^k(\tau,x)-{{\boldsymbol{c}}}(\tau,x)\Big|d\tau dx +\int_{\Gamma_{\boldsymbol{b}}} \int_s^t\Big|{{\boldsymbol{c}}}(\tau,x)-\boldsymbol{b}(\tau,x)\Big|d\tau dx\\
&\overset{6}{\leq} \limsup_{k\to +\infty} \int_{\mathbb{T}^d}\int_s^t\Big|\boldsymbol{b}^k(\tau,x)-\boldsymbol{b}(\tau,x)\Big|d\tau dx +2\int_{\mathbb{T}^d} \int_s^t\Big|{{\boldsymbol{c}}}(\tau,x)-\boldsymbol{b}(\tau,x)\Big|d\tau dx\\
&\overset{7}{=}2\int_{\mathbb{T}^d} \int_s^t\Big|{{\boldsymbol{c}}}(\tau,x)-\boldsymbol{b}(\tau,x)\Big|d\tau dx \lt 2\varepsilon.
\end{aligned}
\end{equation*}1 follows by a triangular inequality, 2 follows because the functional
\begin{equation*}
\Gamma_{\boldsymbol{b}} \ni \gamma \longmapsto \Big|\gamma(t)-\gamma(s)-\int_s^t{{\boldsymbol{c}}}(\tau,\gamma(\tau))d\tau\Big|\in \mathbb{R}
\end{equation*} is continuous, 3 follows because 
$\boldsymbol{\eta}^k$ is concentrated on integral curves of 
$\boldsymbol{b}^k$, 4 follows by bringing the absolute value inside the integral, 5 follows because 
$(e_\tau)_\#\boldsymbol{\eta}^k=\mathscr{L}^{d}=(e_\tau)_\#\boldsymbol{\eta},$ 6 follows by a triangular inequality, and 7 follows since 
$\boldsymbol{b}^k\to \boldsymbol{b}$ in 
$L^1_{loc}$. As 
$\varepsilon$ was arbitrary, (2.6) follows. Therefore 
$\boldsymbol{\eta}$ is a Lagrangian representation of 
$(1,\boldsymbol{b})$. By the first part of Theorem 1.10 we have already proved, we know that there exists a unique Lagrangian representation 
$\boldsymbol{\eta}$ of 
$(1,\boldsymbol{b})$. Therefore, the whole sequence 
$\boldsymbol{\eta}^k$ converges narrowly to 
$\boldsymbol{\eta}$ as 
$k\to+\infty$. This proves the thesis.
3. Stochasticity
We will now prove part 
$(iii)$ of Theorem 1.10. Throughout this section, 
$\boldsymbol{\eta}$ is the unique Lagrangian representation of 
$(1,\boldsymbol{b})$ from the first part of Theorem 1.10. Recall that we have fixed a regular measurable selection 
$\{\gamma_{1,y}\}$ of integral curves of 
$\boldsymbol{b}$ starting from 
$1$ and that
\begin{equation*}\boldsymbol{\eta}=\int_{\mathbb{T}^d}{{\boldsymbol{\delta}}}_{\gamma_{1,y}}dy.\end{equation*} We also define the measure 
${\boldsymbol{\nu}} =(e_0,e_1)_\#\boldsymbol{\eta}$ on 
$\mathbb{T}^d\times\mathbb{T}^d$. For every 
$x\in \mathbb{T}^d,$ we define the family of measures on 
$\Gamma_{\boldsymbol{b}}$
\begin{equation}
{{\boldsymbol{\delta}}}_{x,\gamma_{1,y}}:=\left\{
\begin{aligned}
{{\boldsymbol{\delta}}}_{\gamma_{1,y}}\qquad &\text{if} \quad \gamma_{1,y}(0)=x,\\
0\qquad &\text{if}\quad \gamma_{1,y}(0)\neq x.
\end{aligned}
\right.
\end{equation}Define the projection maps
\begin{equation*}\pi_0 :\mathbb{T}^d\times\mathbb{T}^d\ni (x,y)\longmapsto x\in \mathbb{T}^d,\end{equation*}and
\begin{equation*}\pi_1 :\mathbb{T}^d\times\mathbb{T}^d\ni (x,y)\longmapsto y\in \mathbb{T}^d.\end{equation*} Let 
$\{{\boldsymbol{\nu}}_x\}$ be a disintegration of 
${\boldsymbol{\nu}}$ with respect to 
$\pi_0$ and 
$\mathscr{L}^{d}$.
3.1. Disintegration of
$\mathbf{\eta}$ with respect to
$\mathbf{{\nu}}$
We will now give an expression for disintegrations of 
${\boldsymbol{\eta}}$ with respect to 
$e_{0}$ and 
$\mathscr{L}^{d}$ in terms of 
$\{\boldsymbol{\nu}_{x}\}$. Throughout this section, 
$\{\boldsymbol{\eta}_{0,x}\}$ is a disintegration of 
$\boldsymbol{\eta}$ with respect to 
$e_0$ and 
$\mathscr{L}^{d}$. We then define 
$\tilde{\boldsymbol{\nu}}_{x} :=(\pi_1)_\#{\boldsymbol{\nu}}_{x}$ for every 
$x\in \mathbb{T}^d$. We also define the probability measure
\begin{equation}
{\boldsymbol{\mu}}_y:={{\boldsymbol{\delta}}}_{(\gamma_{1,y}(0),y)},
\end{equation} on 
$\mathbb{T}^d\times \mathbb{T}^d$ for every 
$y\in \mathbb{T}^d$.
Lemma 3.1. The family 
$\{{\boldsymbol{\mu}}_y\}$ is a disintegration of 
${\boldsymbol{\nu}}$ with respect to 
$\pi_1$ and 
$\mathscr{L}^{d}.$
Proof. It is clear that 
${\boldsymbol{\mu}}_y$ is supported on 
$\pi_1^{-1}(y)$. By part 
$(i)$ of Theorem 1.10, we know also that 
$\{{{\boldsymbol{\delta}}}_{\gamma_{1,y}} \}$ is a disintegration of 
$\boldsymbol{\eta}$ with respect to 
$e_1$ and 
$\mathscr{L}^{d}$. Therefore, for every Borel set 
$A$ in 
$\mathbb{T}^d\times \mathbb{T}^d$, we have
\begin{equation*}{\boldsymbol{\nu}}(A)=(e_0,e_1)_\#\boldsymbol{\eta}(A)= \int_{\mathbb{T}^d} (e_0,e_1)_\#{{\boldsymbol{\delta}}}_{\gamma_{1,y}} (A)dy=\int_{\mathbb{T}^d} {{\boldsymbol{\delta}}}_{(\gamma_{1,y}(0),y)}(A)dy=\int_{\mathbb{T}^d}{\boldsymbol{\mu}}_y(A)dy,\end{equation*}which proves the thesis.
Lemma 3.2. The family 
$\{{{\boldsymbol{\delta}}}_{x,\gamma_{1,y}}: x,y\in \mathbb{T}^d\}$ is a disintegration of 
$\boldsymbol{\eta}$ with respect to 
$(e_{0},e_1)$ and 
${\boldsymbol{\nu}}$.
Proof. It is clear that 
${{\boldsymbol{\delta}}}_{x,\gamma_{1,y}}$ is supported on 
$(e_0,e_1)^{-1} (x,y)$. For every Borel set 
$A$ contained in 
$\Gamma_{\boldsymbol{b}}$, we have
\begin{equation}
\begin{aligned}
\int_{\mathbb{T}^d\times\mathbb{T}^d}{{\boldsymbol{\delta}}}_{x,\gamma_{1,y}}(A) {\boldsymbol{\nu}}(dx,dy)&=\int_{\mathbb{T}^d}\int_{\mathbb{T}^d\times \{y\}} {{\boldsymbol{\delta}}}_{x,\gamma_{1,y}}(A) d{\boldsymbol{\mu}}_ydy\\
&=\int_{\mathbb{T}^d} {{\boldsymbol{\delta}}}_{\gamma_{1,y}}(A)dy\\
&=\boldsymbol{\eta}(A),
\end{aligned}
\end{equation} where in the first equality we have used Lemma 3.1, as well as (1.11). In the second equality we have used the definition (3.2) of 
${\boldsymbol{\mu}}_y$ and the definition (3.1) of 
${{\boldsymbol{\delta}}}_{x,\gamma_{1,y}}$, and in the last equality we have used that 
$\{{{\boldsymbol{\delta}}}_{\gamma_{1,y}}\}$ is a disintegration of 
$\boldsymbol{\eta}$ with respect to 
$e_1$ and 
$\mathscr{L}^{d}$, which follows from 
$(i)$ of Theorem 1.10, which we have already proved. This proves the claim.
Lemma 3.3. For 
$\mathscr{L}^{d}$-a.e. 
$x\in \mathbb{T}^d$, we have
\begin{equation}
\boldsymbol{\eta}_{0,x}=\int_{\mathbb{T}^d}{{\boldsymbol{\delta}}}_{\gamma_{1,y}}d\tilde{\boldsymbol{\nu}}_x.
\end{equation}Proof. Let 
$B$ be a Borel set contained in 
$\mathbb{T}^d$. As 
$\Gamma_{\boldsymbol{b}}$ is separable, its Borel 
$\sigma$-algebra is generated by a countable family 
$\mathscr{G}$. Let 
$A\in \mathscr{G}$. We then have
\begin{equation}
\begin{aligned}\int_B \boldsymbol{\eta}_{0,x}(A)dx
&\overset{1}{=}\int_{\mathbb{T}^d} \boldsymbol{\eta}_{0,x}(A\cap\{\gamma(0)\in B\})dx\\
&\overset{2}{=}\boldsymbol{\eta}(A\cap\{\gamma(0)\in B\})\\
&\overset{3}{=}\int_{\mathbb{T}^d\times\mathbb{T}^d} {{\boldsymbol{\delta}}}_{x,\gamma_{1,y}}(A\cap\{\gamma(0)\in B\}){\boldsymbol{\nu}}(dx,dy)\\
&\overset{4}{=}\int_B\Big[ \int_{\{x\}\times\mathbb{T}^d} {{\boldsymbol{\delta}}}_{x,\gamma_{1,y}}(A) d{\boldsymbol{\nu}}_x\Big]dx \\
&\overset{5}{=}\int_B\Big[\int_{\mathbb{T}^d}{{\boldsymbol{\delta}}}_{\gamma_{1,y}}(A)\tilde{\boldsymbol{\nu}}_x(dy)\Big]dx.
\end{aligned}
\end{equation} In equality 
$1$, we have used that 
$\boldsymbol{\eta}_{0,x}$ is supported on 
$\{\gamma(0)=x\}$ for every 
$x\in\mathbb{T}^d$. In equality 
$2$, we have used that 
$\{\boldsymbol{\eta}_{0,x}\}$ is a disintegration of of 
$\boldsymbol{\eta}$ with respect to 
$e_0$ and 
$\mathscr{L}^{d}$. In equality 
$3$, we have used Lemma 3.2. In equality 
$4$, we have used that 
$\{{\boldsymbol{\nu}}_x\}$ is a disintegration of 
${\boldsymbol{\nu}}$ with respect to 
$\pi_0$ and 
$\mathscr{L}^{d}$, equation (1.11), as well as the fact that 
${{\boldsymbol{\delta}}}_{x,\gamma_{1,y}}(A\cap \{\gamma(0)\in B\})=0$ if 
$x\notin B$ by definition. In equality 
$5$, we have used the definition of 
${{\boldsymbol{\delta}}}_{x,\gamma_{1,y}}$ as well as the definition of 
$\{\tilde{\boldsymbol{\nu}}_x\}$. As 
$B$ was an arbitrary Borel set in 
$\mathbb{T}^d$, there exists a set 
$N_A$ of vanishing Lebesgue measure such that for every 
$x\in \mathbb{T}^d-N_A$, we have
\begin{equation*}\boldsymbol{\eta}_{0,x}(A)=\int_{\mathbb{T}^d}{{\boldsymbol{\delta}}}_{\gamma_{1,y}}(A)\tilde{\boldsymbol{\nu}}_x(dy).\end{equation*}Now define
\begin{equation*}N:=\bigcup_{A\in \mathscr{G}}N_A,\end{equation*} which is a set of vanishing Lebesgue measure. Then, for every 
$A\in \mathscr{G}$ and every 
$x\in \mathbb{T}^d- N$, we have
\begin{equation}
\boldsymbol{\eta}_{0,x}(A)=\int_{\mathbb{T}^d}{{\boldsymbol{\delta}}}_{\gamma_{1,y}}(A)\tilde{\boldsymbol{\nu}}_x(dy).
\end{equation} As 
$\mathscr{G}$ generates the Borel 
$\sigma$-algebra of 
$\Gamma_{\boldsymbol{b}}$, the thesis is proved.
3.2. Proof of
$(iii)$ of Theorem 1.10
We now conclude the proof of Theorem 1.10.
Proof. Recall that 
$\boldsymbol{\eta}$ is the unique Lagrangian representation of 
$(1,\boldsymbol{b})$ from the first part of Theorem 1.10, and that we have fixed a regular measurable selection 
$\{\gamma_{1,y}\}$ of integral curves of 
$\boldsymbol{b}$. In view of Lemma 3.3, there exists a Borel family of probability measures 
$\{\tilde{\boldsymbol{\nu}}_x\}$ defined in 
$\S$ 3.1 such that
\begin{equation}
\boldsymbol{\eta}_{0,x}=\int_{\mathbb{T}^d}{{\boldsymbol{\delta}}}_{\gamma_{1,y}}\tilde{\boldsymbol{\nu}}_x(dy),
\end{equation} for 
$\mathscr{L}^{d}$-a.e. 
$x\in \mathbb{T}^d$, which is the first part the statement of part 
$(iii)$ of Theorem 1.10.
Let us now show that for the vector field 
$\boldsymbol{b}_{DP}:[0,1]\times \mathbb{T}^2\to \mathbb{R}^2$ constructed by Depauw, the family probability measures 
$\tilde{\boldsymbol{\nu}}_x$ are not Dirac masses for 
$\mathscr{L}^{2}$-a.e. 
$x\in \mathbb{T}^2$. From the Appendix, we have that 
$\rho^B, \;\rho^W:[0,1]\times \mathbb{T}^2\to \mathbb{R}^+$ are two bounded densities in 
$C([0,1];w^*-L^\infty(\mathbb{T}^2))$ such that:
(i)
$\rho^B(1,\boldsymbol{b}_{DP})$ and
$\rho^W(1,\boldsymbol{b}_{DP})$ solve (PDE);(ii)
$\rho^B(0,\cdot)=1/2=\rho^W(0,\cdot)$;(iii)
$\rho^B(t,\cdot)+\rho^W(t,\cdot)=1$ for every
$t\in[0,1]$;(iv)
$\operatorname{supp}\rho^B(1,\cdot)\cup \operatorname{supp}\rho^W(1,\cdot)=\mathbb{T}^2$;(v)
$\operatorname{supp}\rho^B(1,\cdot)\cap \operatorname{supp}\rho^W(1,\cdot)$ is of vanishing Lebesgue measure.
Let 
$\boldsymbol{\eta}^B$ and 
$\boldsymbol{\eta}^W$ be two Lagrangian representations of 
$\rho^B(1,\boldsymbol{b}_{DP})$ and 
$\rho^W(1,\boldsymbol{b}_{DP})$ respectively, whose existence follows from the superposition principle. Let 
${\boldsymbol{\nu}}^B$ and 
${\boldsymbol{\nu}}^W$ be two probability measures given by 
${\boldsymbol{\nu}}^B=(e_0,e_1)_\#\boldsymbol{\eta}^B$ and 
${\boldsymbol{\nu}}^W=(e_0,e_1)_\#\boldsymbol{\eta}^W$. Let 
$\{\boldsymbol{\eta}_{0,x}^B\}$ be a disintegration of 
$\boldsymbol{\eta}^B$ with respect to 
$e_0$ and 
$\mathscr{L}^{2}$, and let 
$\{{\boldsymbol{\nu}}_x^B\}$ be a disintegration of 
${\boldsymbol{\nu}}^B$ with respect to 
$\pi_0$ and 
$\mathscr{L}^{2}$. Similarly, let 
$\{\boldsymbol{\eta}_{0,x}^W\}$ be a disintegration of 
$\boldsymbol{\eta}^W$ with respect to 
$e_0$ and 
$\mathscr{L}^{2}$, and let 
$\{{\boldsymbol{\nu}}_x^W\}$ be a disintegration of 
${\boldsymbol{\nu}}^W$ with respect to 
$\pi_0$ and 
$\mathscr{L}^{2}$. Note that by definition of 
${\boldsymbol{\nu}}^B$ and 
${\boldsymbol{\nu}}^W$, we have
\begin{equation*}(\pi_1)_\#{\boldsymbol{\nu}}^B=(e_1)_\#\boldsymbol{\eta}^B\qquad\text{and}\qquad (\pi_1)_\#{\boldsymbol{\nu}}^W=(e_1)_\#\boldsymbol{\eta}^W.\end{equation*} This clearly implies that for 
$\mathscr{L}^{2}$-a.e. 
$x\in\mathbb{T}^2$, we have
\begin{equation}
(\pi_1)_\#{\boldsymbol{\nu}}^B_x=(e_1)_\#\boldsymbol{\eta}_{0,x}^B \qquad\text{and} \qquad (\pi_1)_\#{\boldsymbol{\nu}}^W_x=(e_1)_\#\boldsymbol{\eta}_{0,x}^W.
\end{equation}Therefore, we have
\begin{equation*}
\begin{aligned}
\int_{\mathbb{T}^2}(\pi_1)_\#{\boldsymbol{\nu}}^B_x(\operatorname{supp} \rho^W(1,\cdot))dx&=\int_{\mathbb{T}^2}(e_1)_\#\boldsymbol{\eta}^B_x(\operatorname{supp}\rho^W(1,\cdot))dx\\
&=(e_1)_\#\boldsymbol{\eta}^B(\operatorname{supp} \rho^W(1,\cdot))\\
&=\int_{\operatorname{supp}\rho^W(1,\cdot)}\rho^B(1,x)dx\\
&=0.
\end{aligned}
\end{equation*}Similarly, we have
\begin{equation*}
\int_{\mathbb{T}^2}(\pi_1)_\#{\boldsymbol{\nu}}^W_x(\operatorname{supp} \rho^B(1,\cdot))dx=0.
\end{equation*} Therefore, for 
$\mathscr{L}^{2}$-a.e. 
$x\in\mathbb{T}^2$, in view of property (iv) above, the probability measures 
$(\pi_1)_\#{\boldsymbol{\nu}}^W_x$ and 
$(\pi_1)_\#{\boldsymbol{\nu}}^B_x$ are mutually singular. Also, by property (iii) above, and by uniqueness of the Lagrangian representation of 
$(1,\boldsymbol{b})$, we have that
\begin{equation}
\boldsymbol{\eta}=\frac{1}{2}(\boldsymbol{\eta}^B+\boldsymbol{\eta}^W).
\end{equation} By essential uniqueness of the disintegration, we therefore have for 
$\mathscr{L}^{2}$-a.e. 
$x\in \mathbb{T}^2$
\begin{equation*}
{\boldsymbol{\nu}}_x=\frac{1}{2}({\boldsymbol{\nu}}^W_x+{\boldsymbol{\nu}}^B_x).
\end{equation*} Therefore, for 
$\mathscr{L}^{2}$-a.e. 
$x\in\mathbb{T}^2$, we have
\begin{equation*}
\tilde{\boldsymbol{\nu}}_x=(\pi_1)_\#{\boldsymbol{\nu}}_x=\frac{1}{2}(((\pi_1)_\#{\boldsymbol{\nu}}^W_x+(\pi_1)_\#{\boldsymbol{\nu}}^B_x).
\end{equation*} whereby for 
$\mathscr{L}^{2}$-a.e. 
$x\in \mathbb{T}^2$ the probability measure 
$\tilde{\boldsymbol{\nu}}_x$ is not a Dirac mass. This concludes the proof of 
$(iii)$ of Theorem 1.10.
Appendix
We construct the bounded, divergence-free vector field 
$\boldsymbol{b}_{DP}:[0,1]\times\mathbb{T}^2\to \mathbb{R}^2$ of Depauw from [Reference Depauw8], as well as two densities 
$\rho^W,\rho^B:[0,1]\times \mathbb{T}^2\to \mathbb{R}^+$ such that the vector fields 
$\rho^W(1,\boldsymbol{b}_{DP})$ and 
$\rho^B(1,\boldsymbol{b}_{DP}) $ solve (PDE), and have the following properties:
(1)
$\rho^B(1,\boldsymbol{b}_{DP})$ and
$\rho^W(1,\boldsymbol{b}_{DP})$ solve (PDE);(2)
$\rho^B(0,\cdot)=1/2=\rho^W(0,\cdot)$;(3)
$\rho^B(t,\cdot)+\rho^W(t,\cdot)=1$ for every
$t\in[0,1]$;(4)
$\operatorname{supp}\rho^B(1,\cdot)\cup \operatorname{supp}\rho^W(1,\cdot)=\mathbb{T}^2$;(5)
$\operatorname{supp}\rho^B(1,\cdot)\cap \operatorname{supp}\rho^W(1,\cdot)$ is of vanishing Lebesgue measure.
We follow closely the construction of a similar vector field given in [Reference De Lellis and Giri6].
Introduce the following two lattices on 
$\mathbb R^2$, namely 
$\mathcal{L}^1 := \mathbb Z^2\subset \mathbb R^2$ and 
$\mathcal{L}^2:=\mathbb Z^2 + (\frac{1}{2}, \frac{1}{2})\subset \mathbb R^2$. To each lattice, associate a subdivision of the plane into squares, which have vertices lying in the corresponding lattices, which we denote by 
$\mathcal{S}^1$ and 
$\mathcal{S}^2$. Then consider the rescaled lattices 
$\mathcal{L}^1_k:= 2^{-k} \mathbb{Z}^2$ and 
$\mathcal{L}^2_k := (2^{-k-1},2^{-k-1})+2^{-k} \mathbb Z^2$ and the corresponding square subdivision of 
$\mathbb Z^2$, respectively 
$\mathcal{S}^1_k$ and 
$\mathcal{S}^2_k$. Observe that the centres of the squares 
$\mathcal{S}^1_k$ are elements of 
$\mathcal{L}^2_k$ and viceversa.
Next, define the following 
$2$-dimensional autonomous vector field:
\begin{equation*}
{{\boldsymbol{w}}}(x) =
\begin{cases}
(0, 4x_1)^t\text{, if }1/2 \gt |x_1| \gt |x_2| \\
(-4x_2, 0)^t\text{, if }1/2 \gt |x_2| \gt |x_1| \\
(0, 0)^t\text{, otherwise.} \\
\end{cases}
\end{equation*} 
${{\boldsymbol{w}}}$ is a bounded, divergence-free vector field, whose derivative is a finite matrix-valued Radon measure given by
\begin{equation*}
\begin{aligned}
D{{\boldsymbol{w}}}(x_1,x_2) =
&\begin{pmatrix}
0 & 0 \\
4{\rm sgn}(x_1) & 0
\end{pmatrix}
\mathscr{L}^{2}\lfloor_{\{|x_2| \lt |x_1| \lt 1/2\}} +
\begin{pmatrix}
0 & -4{\rm sgn}(x_2) \\
0 & 0
\end{pmatrix}
\mathscr{L}^{2}\lfloor_{\{|x_1| \lt |x_2| \lt 1/2\}}\\
&+\begin{pmatrix}
4x_2{\rm sgn}(x_1) & -4x_2{\rm sgn}(x_2) \\
4x_1{\rm sgn}(x_1) & -4x_1{\rm sgn}(x_2)
\end{pmatrix}
\mathscr{H}^{1}\lfloor_{\{x_1=x_2,0 \lt |x_1|,|x_2|\leq 1/2\}}.\\
\end{aligned}
\end{equation*} Periodise 
${{\boldsymbol{w}}}$ by defining 
$\Lambda = \{(y_1, y_2) \in \mathbb{Z}^2 : y_1 + y_2 \;\text{is even}\}$ and setting
\begin{equation*}
{{\boldsymbol{u}}}(x) = \sum_{y \in \Lambda} {{\boldsymbol{w}}}(x-y).
\end{equation*} Even though 
${{\boldsymbol{u}}}$ is non-smooth (see Figure 1), it is in 
$BV_{loc}(\mathbb{R}^2;\mathbb{R}^2)$. By the theory of regular Lagrangian flows (see for instance [Reference Ambrosio and Crippa3]), there exists a unique incompressible almost everywhere defined flow 
${{\boldsymbol{X}}}$ along 
${{\boldsymbol{u}}}$ can be described explicitely.
(R) The map
${{\boldsymbol{X}}} (t,0 ,\cdot)$ is Lipschitz on each square
$S$ of
$\mathcal{S}^2$ and
${{\boldsymbol{X}}} (1/2,0, \cdot)$ is a clockwise rotation of
$\pi/2$ radians of the “filled”
$S$, while it is the identity on the “empty ones”. In particular for every
$j\geq 1,$
${{\boldsymbol{X}}} (1/2,0, \cdot)$ maps an element of
$\mathcal{S}^1_j$ rigidly onto another element of
$\mathcal{S}^1_j$. For
$j=1$ we can be more specific. Each
$S\in \mathcal{S}^2$ is formed precisely by
$4$ squares of
$\mathcal{S}^1_1$: in the case of “filled”
$S$ the
$4$ squares are permuted in a
$4$-cycle clockwise, while in the case of “empty”
$S$ the
$4$ squares are kept fixed.
Figure 1. Action of the flow of 
${{\boldsymbol{u}}}$ from 
$t=0$ to 
$t=1/2$. The shaded region denotes the set 
$\{\rho^B=1\}$. The figure is from [Reference De Lellis and Giri6].
Let 
$\rho^B:[1/2,1]\times \mathbb{R}^2\to \mathbb{R}^+$ be the unique density such that 
$\rho^B(1,{{\boldsymbol{u}}})$ solves (PDE) and 
$\rho^B(1,\cdot)=\lfloor{x_1}\rfloor /2+ \lfloor{x_2}\rfloor/2 \ mod \ 2=:\bar\rho^B$. Then, we have the following formula 
${{\boldsymbol{X}}}(t,0,\cdot)_\#\bar\rho^B\mathscr{L}^{d}=\rho^B(t,x)\mathscr{L}^{d}$. Using property (R), we have
\begin{equation}
\rho^B(1/2, x) = 1 - \bar\rho^B(2x).
\end{equation} We define 
$\boldsymbol{b}_{DP}:[0,1]\times\mathbb{R}^2\to\mathbb{R}^2$ as follows. Set 
$\boldsymbol{b}_{DP}(t, x) = {{\boldsymbol{u}}}(x)$ for 
$1/2 \lt t\leq1$ and 
$\boldsymbol{b}_{DP}(t, x) = {{\boldsymbol{u}}}(2^k x)$ for 
$1/2^{k+1} \lt t\leq1/2^{k}$. Let 
$\rho^B:[0,1]\times \mathbb{R}^2\to \mathbb{R}^+$ be the unique density such that 
$\rho^B(1,{{\boldsymbol{u}}})$ solves (PDE) with 
$\rho^B(0,\cdot)=\lfloor{x_1}\rfloor/2 + \lfloor{x_2}\rfloor/2 \ mod \ 2=:\bar\rho^B$ Moreover, using recursively the appropriately scaled version of (3.10), we can check that
\begin{equation*}
\rho^B(1/2^{k}, x) = \bar\rho^B (2^{k} x) \quad\text{for k even,}\qquad \rho^B (1/2^{k}, x) =1- \bar\rho^B (2^{k} x)\quad\text{for k odd. }
\end{equation*}Define the density 
$\rho^W(t,x):=1-\rho^B(t,x)$. Then 
$\rho^W(1,\boldsymbol{b}_{DP})$ also solves (PDE), by linearity. As the construction we have performed is 
$\mathbb{Z}^2$-periodic, we may consider 
$\boldsymbol{b}_{DP}$, 
$\rho^W,$ and 
$\rho^B$ to be defined on 
$[0,1]\times \mathbb{T}^2$. Properties (i)-(v) follow directly from the construction.
Acknowledgements
The author is thankful to his advisor Nikolay Tzvetkov for his support. The author is thankful to Stefano Bianchini for enlightening discussions on measure theory and on the disintegration of a measure. The author acknowledges the hospitality of the Pitcho Centre for Scientific Studies where this work was done. The author is thankful to the anonymous referee for useful suggestions.
Open access
