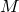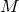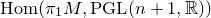A properly convex domain is a convex open set in real-projective space whose closure contains no projective line. The quotient of such a domain by a discrete torsion-free group of projective transformations that preserve the domain is a properly convex manifold. If, in addition, the frontier of the domain contains no segment of a projective line bigger than one point, then the manifold is strictly convex. A hyperbolic manifold is a strictly convex projective manifold.
The case of dimension
![]() $2$
had been much studied. This is the simplest case of higher Teichmüller theory. A basic result is that a strictly convex structure on a closed manifold is uniquely determined by the conjugacy class of the holonomy homomorphism into the projective general linear group. Moreover, if the dimension of the manifold is at least
$2$
had been much studied. This is the simplest case of higher Teichmüller theory. A basic result is that a strictly convex structure on a closed manifold is uniquely determined by the conjugacy class of the holonomy homomorphism into the projective general linear group. Moreover, if the dimension of the manifold is at least
![]() $2$
, then the holonomies that arise are precisely those in certain topological components of the representation variety. The goal of this paper is to provide self-contained proofs of these results.
$2$
, then the holonomies that arise are precisely those in certain topological components of the representation variety. The goal of this paper is to provide self-contained proofs of these results.
If
![]() $G$
is a Lie group, and
$G$
is a Lie group, and
![]() $X$
is a manifold on which
$X$
is a manifold on which
![]() $G$
acts analytically and transitively, then a
$G$
acts analytically and transitively, then a
![]() $(G,X)$
-structure on a manifold is a maximal collection of charts which take values in
$(G,X)$
-structure on a manifold is a maximal collection of charts which take values in
![]() $X$
and such that the transition functions are in
$X$
and such that the transition functions are in
![]() $G$
. For such structures, the Ehresmann–Thurston principle says that when
$G$
. For such structures, the Ehresmann–Thurston principle says that when
![]() $M$
is closed (compact without boundary), then the set of holonomies of
$M$
is closed (compact without boundary), then the set of holonomies of
![]() $(G,X)$
-structures is an open subset of the representation variety. However, properly convex structures do not fit into this scheme. The basic issue is that the convex open set in projective space varies. The set of such holonomies is often not closed. For example, the space of hyperbolic structures on the circle is not closed in
$(G,X)$
-structures is an open subset of the representation variety. However, properly convex structures do not fit into this scheme. The basic issue is that the convex open set in projective space varies. The set of such holonomies is often not closed. For example, the space of hyperbolic structures on the circle is not closed in
![]() $\textrm {PO}(1,1)$
. In general, the space of all projective structures on a manifold of dimension larger than
$\textrm {PO}(1,1)$
. In general, the space of all projective structures on a manifold of dimension larger than
![]() $2$
is mysterious.
$2$
is mysterious.
If
![]() $M$
is a compact
$M$
is a compact
![]() $n$
-manifold, then
$n$
-manifold, then
![]() $\textrm {Rep}(M)={\textrm {Hom}}(\pi _1M,\textrm {PGL}(n+1,{\mathbb{R}}))$
is a real algebraic variety. Let
$\textrm {Rep}(M)={\textrm {Hom}}(\pi _1M,\textrm {PGL}(n+1,{\mathbb{R}}))$
is a real algebraic variety. Let
![]() $\textrm {Rep}_{P}(M)$
and
$\textrm {Rep}_{P}(M)$
and
![]() $\textrm {Rep}_{S}(M)$
be, respectively, the subsets of
$\textrm {Rep}_{S}(M)$
be, respectively, the subsets of
![]() $\textrm {Rep}(M)$
of holonomies of properly convex, and of strictly convex structures on
$\textrm {Rep}(M)$
of holonomies of properly convex, and of strictly convex structures on
![]() $M$
. Then
$M$
. Then
![]() $\textrm {Rep}_S(M)\subseteq \textrm {Rep}_P(M)$
. Throughout this paper we use the Euclidean topology everywhere, and not the Zariski topology. In the following,
$\textrm {Rep}_S(M)\subseteq \textrm {Rep}_P(M)$
. Throughout this paper we use the Euclidean topology everywhere, and not the Zariski topology. In the following,
![]() $M$
is closed and
$M$
is closed and
![]() $n\geqslant 2$
.
$n\geqslant 2$
.
1. Open Theorem.
![]() $\textrm {Rep}_{P}(M)$
is open in
$\textrm {Rep}_{P}(M)$
is open in
![]() $\textrm {Rep}(M)$
.
$\textrm {Rep}(M)$
.
2. Closed Theorem.
![]() $\textrm {Rep}_{S}(M)$
is closed in
$\textrm {Rep}_{S}(M)$
is closed in
![]() $\textrm {Rep}(M)$
.
$\textrm {Rep}(M)$
.
3. Clopen Theorem. Then
![]() $\textrm {Rep}_S(M)$
is a union of connected components of
$\textrm {Rep}_S(M)$
is a union of connected components of
![]() $\textrm {Rep}(M)$
.
$\textrm {Rep}(M)$
.
It follows from (1.15) that the holonomy of a strictly convex structure uniquely determines a projective manifold up to projective isomorphism. The Open Theorem is due to Koszul [Reference KoszulKos65, Reference KoszulKos68]. Our proof is distilled from his. There is an affine manifold that is the tautological line bundle over a projective manifold,
![]() $M$
. Then
$M$
. Then
![]() $M$
is properly convex if and only if there is an outwards-convex section of this bundle such that every connected flat subset of the section is contained in a simplex. This type of convexity is easily shown to be preserved by small deformations.
$M$
is properly convex if and only if there is an outwards-convex section of this bundle such that every connected flat subset of the section is contained in a simplex. This type of convexity is easily shown to be preserved by small deformations.
The Closed Theorem when
![]() $n=2$
is due to Choi and Goldman [Reference Choi and GoldmanCG93, Reference Choi and GoldmanCG05], to Kim [Reference KimKim01] when
$n=2$
is due to Choi and Goldman [Reference Choi and GoldmanCG93, Reference Choi and GoldmanCG05], to Kim [Reference KimKim01] when
![]() $n=3$
and to Benoist [Reference BenoistBen05] in general. Our proof is new, and based on a geometric argument called the box estimate (4.3). Given a sequence of strictly convex projective structures whose holonomies converge, the associated domains might degenerate. Benzécri’s compactness theorem [Reference BenzécriBen60] implies one may apply projective transformations so that the domains converge to a properly convex domain, but then the holonomies might diverge. The box estimate implies that if one chooses the conjugacies carefully, then the holonomies also converge. This involves an elementary geometric fact (2.8) about an analogue of centroids for subsets of the sphere.
$n=3$
and to Benoist [Reference BenoistBen05] in general. Our proof is new, and based on a geometric argument called the box estimate (4.3). Given a sequence of strictly convex projective structures whose holonomies converge, the associated domains might degenerate. Benzécri’s compactness theorem [Reference BenzécriBen60] implies one may apply projective transformations so that the domains converge to a properly convex domain, but then the holonomies might diverge. The box estimate implies that if one chooses the conjugacies carefully, then the holonomies also converge. This involves an elementary geometric fact (2.8) about an analogue of centroids for subsets of the sphere.
The Clopen Theorem follows from the Open Theorem and the fact, due to Benoist, that a properly convex manifold that is homeomorphic to a strictly convex manifold is also strictly convex (1.11). We have made an effort to make the paper self-contained by including proofs of all the foundational results needed in Sections 1 and 2. We have endeavoured to simplify these proofs as much as possible. See [Reference BenoistBen08] for an excellent survey.
There are extensions of the Open and Closed Theorems when
![]() $M$
is the interior of a compact manifold with boundary, see [Reference Cooper, Long and TillmannCLT18] and forthcoming work. Indeed, the techniques in this paper were developed to handle this more general situation for which the pre-existing methods do not suffice. But it seems useful to present some of the main ideas in the simplest setting.
$M$
is the interior of a compact manifold with boundary, see [Reference Cooper, Long and TillmannCLT18] and forthcoming work. Indeed, the techniques in this paper were developed to handle this more general situation for which the pre-existing methods do not suffice. But it seems useful to present some of the main ideas in the simplest setting.
1. Properly and strictly convex
This section and the next review some well-known results concerning properly and strictly convex projective manifolds that are needed to prove the theorems. The results needed subsequently are (1.13)–(1.11) at the end of this section. The only mild innovation is that, to avoid appealing to results about word-hyperbolic groups, a more direct approach was taken to the proof of (1.11). The early sections of [Reference Cooper, Long and TillmannCLT15] greatly expand on the background in this section.
If
![]() $M$
is a manifold, the universal cover is
$M$
is a manifold, the universal cover is
![]() $\pi _{M}:\widetilde M \to M$
, and if
$\pi _{M}:\widetilde M \to M$
, and if
![]() $g\in \pi _1M$
, then
$g\in \pi _1M$
, then
![]() $\tau _g:\widetilde M\to \widetilde M$
is the covering transformation corresponding to
$\tau _g:\widetilde M\to \widetilde M$
is the covering transformation corresponding to
![]() $g$
. A geometry is a pair
$g$
. A geometry is a pair
![]() $(G,X)$
, where
$(G,X)$
, where
![]() $G$
is a group that acts analytically and transitively on a manifold
$G$
is a group that acts analytically and transitively on a manifold
![]() $X$
. A
$X$
. A
![]() $(G,X)$
-structure on a manifold
$(G,X)$
-structure on a manifold
![]() $M$
is determined by a development pair
$M$
is determined by a development pair
![]() $(\textrm {dev},\rho )$
that consists of the holonomy
$(\textrm {dev},\rho )$
that consists of the holonomy
![]() $\rho \in {\textrm {Hom}}(\pi _1M,G)$
and the developing map
$\rho \in {\textrm {Hom}}(\pi _1M,G)$
and the developing map
![]() $\textrm {dev}:\widetilde M\to X$
which is a local homeomorphism. The pair satisfies for all
$\textrm {dev}:\widetilde M\to X$
which is a local homeomorphism. The pair satisfies for all
![]() $x\in \widetilde M$
and
$x\in \widetilde M$
and
![]() $g\in \pi _1M$
that
$g\in \pi _1M$
that
![]() $\textrm {dev}(\tau _{g}x)=(\rho g)\textrm {dev} x$
.
$\textrm {dev}(\tau _{g}x)=(\rho g)\textrm {dev} x$
.
In what follows
![]() $V={\mathbb{R}}^{n+1}$
, its dual vector space is
$V={\mathbb{R}}^{n+1}$
, its dual vector space is
![]() $V^*={\textrm {Hom}}(V,{\mathbb{R}})$
, and
$V^*={\textrm {Hom}}(V,{\mathbb{R}})$
, and
![]() ${\mathbb{R}}^{n+1}_0=V_0=V\setminus \{0\}$
. Projective space is
${\mathbb{R}}^{n+1}_0=V_0=V\setminus \{0\}$
. Projective space is
![]() ${\mathbb{P}} V=V_0/{\mathbb{R}}_0$
, and
${\mathbb{P}} V=V_0/{\mathbb{R}}_0$
, and
![]() $[A]\in {\textrm {Aut}}({\mathbb{P}} V)=\textrm {PGL}(V)$
acts on
$[A]\in {\textrm {Aut}}({\mathbb{P}} V)=\textrm {PGL}(V)$
acts on
![]() ${\mathbb{P}} V$
by
${\mathbb{P}} V$
by
![]() $[A][x]=[Ax]$
. Projective geometry is
$[A][x]=[Ax]$
. Projective geometry is
![]() $({\textrm {Aut}}({\mathbb{P}} V),{\mathbb{P}} V)$
and is also written
$({\textrm {Aut}}({\mathbb{P}} V),{\mathbb{P}} V)$
and is also written
![]() $({\textrm {Aut}}(\mathbb{RP}^n),\mathbb{RP}^n)$
. Radiant-affine geometry is
$({\textrm {Aut}}(\mathbb{RP}^n),\mathbb{RP}^n)$
. Radiant-affine geometry is
![]() $(\textrm {GL}(V),V_0)$
.
$(\textrm {GL}(V),V_0)$
.
We use the notation
![]() ${\mathbb{R}}^+=(0,\infty )$
. Positive projective space is
${\mathbb{R}}^+=(0,\infty )$
. Positive projective space is
![]() $\mathbb{RP}^n_+={\mathbb{P}}_+V=V_0/{\mathbb{R}}^+$
and
$\mathbb{RP}^n_+={\mathbb{P}}_+V=V_0/{\mathbb{R}}^+$
and
![]() $[x]_+=\{\lambda x:\lambda \gt 0\}$
for
$[x]_+=\{\lambda x:\lambda \gt 0\}$
for
![]() $x\in V_0$
. Sometimes we identify
$x\in V_0$
. Sometimes we identify
![]() ${\mathbb{P}}_+V$
with the unit sphere
${\mathbb{P}}_+V$
with the unit sphere
![]() $S^n\subset {\mathbb{R}}^{n+1}$
via
$S^n\subset {\mathbb{R}}^{n+1}$
via
![]() $[x]_+\equiv x/\|x\|$
. The group
$[x]_+\equiv x/\|x\|$
. The group
![]() ${\textrm {Aut}}({\mathbb{P}}_+V):=\textrm {SL}_{\pm }(V)\subset \textrm {GL}(V)$
is the subgroup with
${\textrm {Aut}}({\mathbb{P}}_+V):=\textrm {SL}_{\pm }(V)\subset \textrm {GL}(V)$
is the subgroup with
![]() $\det =\pm 1$
. Positive projective geometry
$\det =\pm 1$
. Positive projective geometry
![]() $({\textrm {Aut}}({\mathbb{P}}_+V),{\mathbb{P}}_+V)$
is the double cover of projective geometry. We will pass back and forth between projective geometry and positive projective geometry without mention, often omitting the term positive.
$({\textrm {Aut}}({\mathbb{P}}_+V),{\mathbb{P}}_+V)$
is the double cover of projective geometry. We will pass back and forth between projective geometry and positive projective geometry without mention, often omitting the term positive.
If
![]() $U$
is a vector subspace of
$U$
is a vector subspace of
![]() $V$
, then
$V$
, then
![]() ${\mathbb{P}} U$
is a projective subspace of
${\mathbb{P}} U$
is a projective subspace of
![]() ${\mathbb{P}} V$
. This is a (projective) line if
${\mathbb{P}} V$
. This is a (projective) line if
![]() $\dim U=2$
and a (projective) hyperplane if
$\dim U=2$
and a (projective) hyperplane if
![]() $\dim U=\dim V-1$
. The (projective) dual of
$\dim U=\dim V-1$
. The (projective) dual of
![]() $U$
is the projective subspace
$U$
is the projective subspace
![]() ${\mathbb{P}} U^0\subset {\mathbb{P}} V^*$
where
${\mathbb{P}} U^0\subset {\mathbb{P}} V^*$
where
![]() $U^0=\{\phi \in V^* :\phi (U)=0\}$
. We use the same terminology in positive projective geometry. By lifting developing maps one obtains the following.
$U^0=\{\phi \in V^* :\phi (U)=0\}$
. We use the same terminology in positive projective geometry. By lifting developing maps one obtains the following.
Proposition 1.1.
Every projective structure on
![]() $M$
lifts to a positive projective structure.
$M$
lifts to a positive projective structure.
The frontier of a subset
![]() $X\subset Y$
is
$X\subset Y$
is
![]() $\textrm {Fr} X=\textrm {cl}(X)\setminus \textrm {int}(X)$
, and the boundary is
$\textrm {Fr} X=\textrm {cl}(X)\setminus \textrm {int}(X)$
, and the boundary is
![]() $\partial X=X\cap \textrm {Fr} X$
. A segment is a connected, proper subset of a projective line that contains more than one point. In what follows
$\partial X=X\cap \textrm {Fr} X$
. A segment is a connected, proper subset of a projective line that contains more than one point. In what follows
![]() $\Omega \subset \mathbb{RP}^n$
. If
$\Omega \subset \mathbb{RP}^n$
. If
![]() $H$
is a hyperplane and
$H$
is a hyperplane and
![]() $x\in H\cap \textrm {Fr}\Omega$
and
$x\in H\cap \textrm {Fr}\Omega$
and
![]() $H\cap \textrm {int}\Omega =\emptyset$
, then
$H\cap \textrm {int}\Omega =\emptyset$
, then
![]() $H$
is called a supporting hyperplane (to
$H$
is called a supporting hyperplane (to
![]() $\Omega$
) at
$\Omega$
) at
![]() $x$
. The set
$x$
. The set
![]() $\Omega$
:
$\Omega$
:
-
• is convex if every pair of points in
 $\Omega$
is contained in a segment in
$\Omega$
is contained in a segment in
 $\Omega$
;
$\Omega$
; -
• is properly convex if it is convex, and
 $\textrm {cl}\Omega$
does not contain a projective line;
$\textrm {cl}\Omega$
does not contain a projective line; -
• is strictly convex if it is properly convex and
 $\textrm {Fr}\Omega$
does not contain a segment;
$\textrm {Fr}\Omega$
does not contain a segment; -
• is flat if it is convex and
 $\dim \Omega \lt n$
;
$\dim \Omega \lt n$
; -
• is a convex domain if it is a properly convex open set;
-
• is
 $C^1$
if for each
$C^1$
if for each
 $x\in \textrm {Fr}\Omega$
there is a unique supporting hyperplane at
$x\in \textrm {Fr}\Omega$
there is a unique supporting hyperplane at
 $x$
.
$x$
.
The same terms will be applied to a lift of
![]() $\Omega$
to
$\Omega$
to
![]() ${\mathbb{R}\textrm {P}_+}^n$
. If
${\mathbb{R}\textrm {P}_+}^n$
. If
![]() $V=U\oplus W$
, then projection from
$V=U\oplus W$
, then projection from
![]() ${\mathbb{P}} W$
onto
${\mathbb{P}} W$
onto
![]() ${\mathbb{P}} U$
is
${\mathbb{P}} U$
is
![]() $\pi :{\mathbb{P}} V\setminus {\mathbb{P}} W\longrightarrow {\mathbb{P}} U$
given by
$\pi :{\mathbb{P}} V\setminus {\mathbb{P}} W\longrightarrow {\mathbb{P}} U$
given by
![]() $\pi [u+w]=[u]$
. Duality is the map that sends each point
$\pi [u+w]=[u]$
. Duality is the map that sends each point
![]() $\theta =[\phi ]\in {\mathbb{P}} V^*$
to the hyperplane
$\theta =[\phi ]\in {\mathbb{P}} V^*$
to the hyperplane
![]() $H_{\theta }={\mathbb{P}}\ker \phi \subset {\mathbb{P}} V$
. If
$H_{\theta }={\mathbb{P}}\ker \phi \subset {\mathbb{P}} V$
. If
![]() $L$
is a line in
$L$
is a line in
![]() ${\mathbb{P}} V^*$
the hyperplanes
${\mathbb{P}} V^*$
the hyperplanes
![]() $H_{\theta }$
dual to the points
$H_{\theta }$
dual to the points
![]() $\theta \in L$
are called a pencil of hyperplanes. Then
$\theta \in L$
are called a pencil of hyperplanes. Then
![]() $Q=\cap H_{\theta }$
is the projective dual of
$Q=\cap H_{\theta }$
is the projective dual of
![]() $L$
and is called the core of the pencil. It is a codimension
$L$
and is called the core of the pencil. It is a codimension
![]() $2$
projective subspace.
$2$
projective subspace.
Lemma 1.2.
A convex set
![]() $\Omega$
is properly convex if and only if
$\Omega$
is properly convex if and only if
![]() $\textrm {cl}\Omega$
is disjoint from some hyperplane.
$\textrm {cl}\Omega$
is disjoint from some hyperplane.
Proof.
Without loss of generality, suppose
![]() $\Omega$
is closed. The reverse implication is immediate since the complement of a hyperplane contains no line.
$\Omega$
is closed. The reverse implication is immediate since the complement of a hyperplane contains no line.
Hence, assume
![]() $\Omega$
is properly convex. The result is immediate if
$\Omega$
is properly convex. The result is immediate if
![]() $n=1$
, so assume
$n=1$
, so assume
![]() $n\gt 1$
. Since
$n\gt 1$
. Since
![]() $\Omega$
is convex and contains no projective line, it is simply connected, and so lifts to
$\Omega$
is convex and contains no projective line, it is simply connected, and so lifts to
![]() $\Omega ^{\prime}\subset {\mathbb{R}\textrm {P}_+}^n$
. Let
$\Omega ^{\prime}\subset {\mathbb{R}\textrm {P}_+}^n$
. Let
![]() $H\subset {\mathbb{R}\textrm {P}_+}^n$
be a hyperplane. Then
$H\subset {\mathbb{R}\textrm {P}_+}^n$
be a hyperplane. Then
![]() $H\cap \Omega ^{\prime}$
is empty or properly convex. By induction on dimension,
$H\cap \Omega ^{\prime}$
is empty or properly convex. By induction on dimension,
![]() $H$
contains a projective subspace
$H$
contains a projective subspace
![]() $Q$
with
$Q$
with
![]() $\dim Q=n-2$
that is disjoint from
$\dim Q=n-2$
that is disjoint from
![]() $H\cap \Omega ^{\prime}$
. There is a pencil of hyperplanes
$H\cap \Omega ^{\prime}$
. There is a pencil of hyperplanes
![]() $H_{\theta }$
with core
$H_{\theta }$
with core
![]() $Q$
. Now
$Q$
. Now
![]() $\Omega ^{\prime}\cap H_{\theta }$
is contained in one of the two components of
$\Omega ^{\prime}\cap H_{\theta }$
is contained in one of the two components of
![]() $H_{\theta }\setminus Q$
. As
$H_{\theta }\setminus Q$
. As
![]() $\theta$
moves half way around
$\theta$
moves half way around
![]() ${\mathbb{R}\textrm {P}_+}^1$
the component must change. Thus for some
${\mathbb{R}\textrm {P}_+}^1$
the component must change. Thus for some
![]() $\theta$
the intersection is empty.
$\theta$
the intersection is empty.
In what follows
![]() $\Omega \subset \mathbb{RP}^n$
is a properly convex domain, and
$\Omega \subset \mathbb{RP}^n$
is a properly convex domain, and
![]() ${\textrm {Aut}}(\Omega )\subset {\textrm {Aut}}(\mathbb{RP}^n)$
is the subgroup that preserves
${\textrm {Aut}}(\Omega )\subset {\textrm {Aut}}(\mathbb{RP}^n)$
is the subgroup that preserves
![]() $\Omega$
. The Hilbert metric
$\Omega$
. The Hilbert metric
![]() $d_{\Omega }$
on
$d_{\Omega }$
on
![]() $\Omega$
is defined as follows. If
$\Omega$
is defined as follows. If
![]() $\ell \subset \mathbb{RP}^n$
is a line and
$\ell \subset \mathbb{RP}^n$
is a line and
![]() $\alpha =\Omega \cap \ell \ne \emptyset$
, then
$\alpha =\Omega \cap \ell \ne \emptyset$
, then
![]() $\alpha$
is a proper segment in
$\alpha$
is a proper segment in
![]() $\Omega$
and
$\Omega$
and
![]() $\alpha =(a_-,a_+)$
with
$\alpha =(a_-,a_+)$
with
![]() $a_{\pm }\in \textrm {Fr}\Omega$
. There is a projective isomorphism
$a_{\pm }\in \textrm {Fr}\Omega$
. There is a projective isomorphism
![]() $f:\alpha \rightarrow {\mathbb{R}}^+$
and
$f:\alpha \rightarrow {\mathbb{R}}^+$
and
for
![]() $x,y\in \alpha$
. It follows from the next result that
$x,y\in \alpha$
. It follows from the next result that
![]() $d_{\Omega }$
satisfies the triangle inequality, and thus is a metric. It is a Finsler metric: given by a norm on the tangent space. The factor of
$d_{\Omega }$
satisfies the triangle inequality, and thus is a metric. It is a Finsler metric: given by a norm on the tangent space. The factor of
![]() $1/2$
ensures that this gives the hyperbolic metric when
$1/2$
ensures that this gives the hyperbolic metric when
![]() $\Omega$
is a round disc. A geodesic in
$\Omega$
is a round disc. A geodesic in
![]() $\Omega$
is a curve whose length is the distance between its endpoints. It is immediate that
$\Omega$
is a curve whose length is the distance between its endpoints. It is immediate that
![]() ${\textrm {Aut}}(\Omega )$
acts by isometries of
${\textrm {Aut}}(\Omega )$
acts by isometries of
![]() $d_{\Omega }$
.
$d_{\Omega }$
.
The interior of a triangle in the projective plane is a properly convex domain that is projectively equivalent to the positive quadrant in an affine patch
![]() ${\mathbb{R}}^2$
. A metric ball in this domain with center
${\mathbb{R}}^2$
. A metric ball in this domain with center
![]() $p$
is a hexagon. The vertices of the hexagon lie on the lines through
$p$
is a hexagon. The vertices of the hexagon lie on the lines through
![]() $p$
that contain a vertex of the triangle. A smooth curve in the interior of a triangle is a geodesic for the Hilbert metric if, and only if, the tangent line at each point on the curve intersects the same pair of sides of the triangle. Thus, in a properly convex domain, there may be many geodesics with the same endpoints.
$p$
that contain a vertex of the triangle. A smooth curve in the interior of a triangle is a geodesic for the Hilbert metric if, and only if, the tangent line at each point on the curve intersects the same pair of sides of the triangle. Thus, in a properly convex domain, there may be many geodesics with the same endpoints.
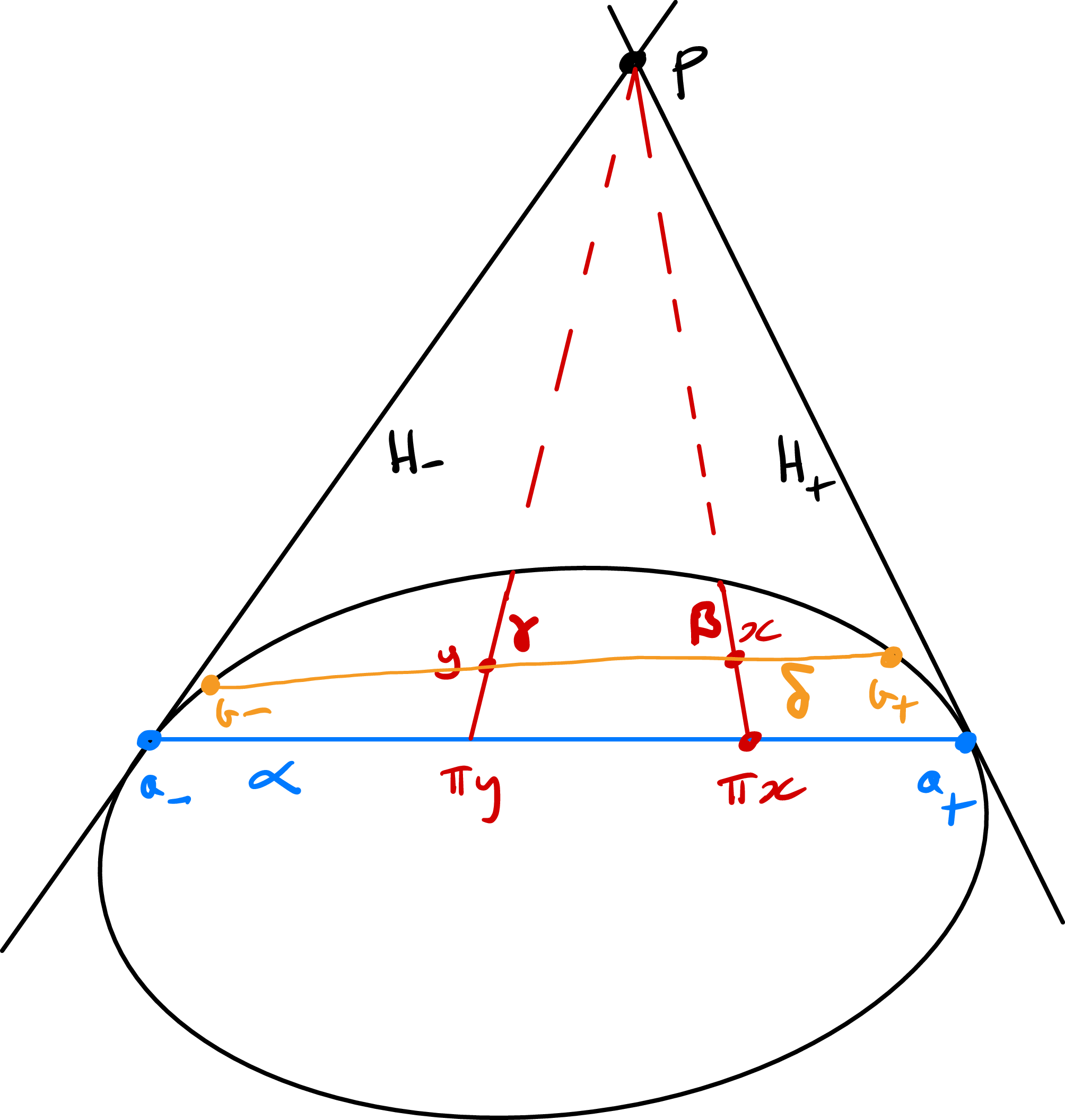
Let
![]() $H_{\pm }$
be supporting hyperplanes for
$H_{\pm }$
be supporting hyperplanes for
![]() $\Omega$
at
$\Omega$
at
![]() $a_{\pm }\in \textrm {Fr}\Omega$
, and
$a_{\pm }\in \textrm {Fr}\Omega$
, and
![]() $P=H_+\cap H_-$
. Projection from
$P=H_+\cap H_-$
. Projection from
![]() $P$
onto
$P$
onto
![]() $\alpha$
is the map
$\alpha$
is the map
![]() $\pi :\Omega \to \alpha =(a_-,a_+)$
given by
$\pi :\Omega \to \alpha =(a_-,a_+)$
given by
![]() $\pi [u+v]=[v]$
where
$\pi [u+v]=[v]$
where
![]() $[u]\in P$
and
$[u]\in P$
and
![]() $[v]\in \alpha$
. The choice of
$[v]\in \alpha$
. The choice of
![]() $H_{\pm }$
is unique only if
$H_{\pm }$
is unique only if
![]() $a_{\pm }$
are
$a_{\pm }$
are
![]() $C^1$
points. If
$C^1$
points. If
![]() $\Omega$
is strictly convex, then for each
$\Omega$
is strictly convex, then for each
![]() $x\in \Omega$
by (1.3)(iii) there is a unique point
$x\in \Omega$
by (1.3)(iii) there is a unique point
![]() $\Pi (x)\in \alpha$
closest to
$\Pi (x)\in \alpha$
closest to
![]() $x$
, and
$x$
, and
![]() $\Pi :\Omega \rightarrow \alpha$
is continuous and called the nearest point retraction. In general
$\Pi :\Omega \rightarrow \alpha$
is continuous and called the nearest point retraction. In general
![]() $\pi \ne \Pi$
.
$\pi \ne \Pi$
.
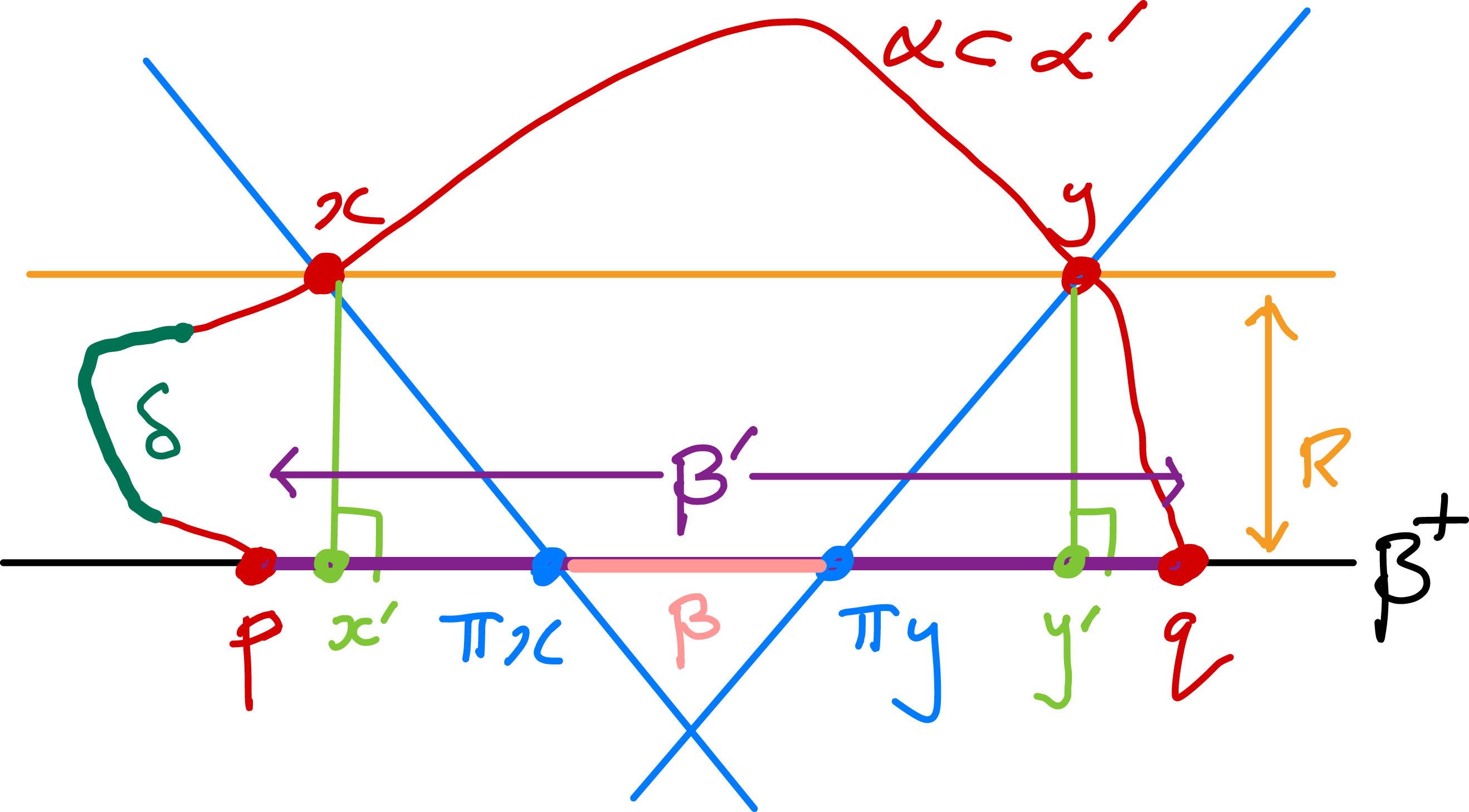
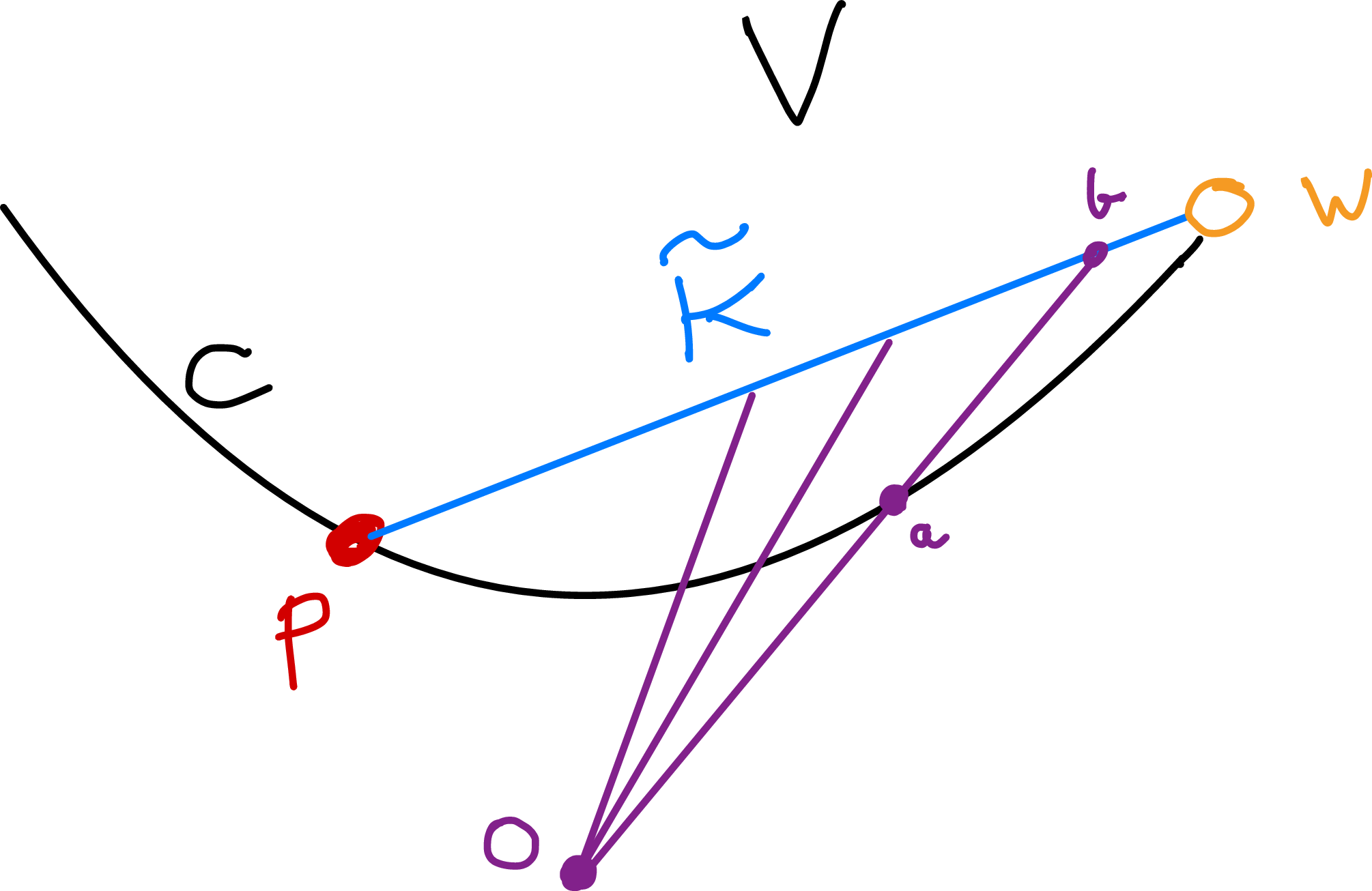
Lemma 1.3. With the preceding notation we have the following:
-
(i)
 $d_{\Omega }(x,y)\geqslant d_{\Omega }(\pi x,\pi y)$
;
$d_{\Omega }(x,y)\geqslant d_{\Omega }(\pi x,\pi y)$
;
Figure 1. Projecting onto a line.
-
(ii) If
 $\Omega$
is strictly convex, then geodesics are segments of lines;
$\Omega$
is strictly convex, then geodesics are segments of lines;
-
(iii) If
 $\Omega$
is strictly convex, then
$\Omega$
is strictly convex, then
 $\forall \ y\in \Omega \ \ \{x\in \Omega : d_{\Omega }(x,y)\leqslant 1\}$
is strictly convex.
$\forall \ y\in \Omega \ \ \{x\in \Omega : d_{\Omega }(x,y)\leqslant 1\}$
is strictly convex.
Proof.
Figure 1 represents two or more dimensions. Let
![]() $\delta =(b_-,b_+)$
be the proper segment in
$\delta =(b_-,b_+)$
be the proper segment in
![]() $\Omega$
containing
$\Omega$
containing
![]() $x$
and
$x$
and
![]() $y$
, and
$y$
, and
![]() $\pi :\Omega \rightarrow \alpha$
as above. Then
$\pi :\Omega \rightarrow \alpha$
as above. Then
![]() $d_{\Omega }(x,y)=d_{\delta }(x,y)$
. Since
$d_{\Omega }(x,y)=d_{\delta }(x,y)$
. Since
![]() $(\pi |\delta ):\delta \to \alpha$
is a projective embedding
$(\pi |\delta ):\delta \to \alpha$
is a projective embedding
![]() $d_{\delta }(x,y)=d_{\pi \delta }(\pi x,\pi y)$
. Also
$d_{\delta }(x,y)=d_{\pi \delta }(\pi x,\pi y)$
. Also
![]() $d_{\pi \delta }(\pi x,\pi y)\geqslant d_{\alpha }(\pi x,\pi y)$
because
$d_{\pi \delta }(\pi x,\pi y)\geqslant d_{\alpha }(\pi x,\pi y)$
because
![]() $\pi \delta \subset \alpha$
. Finally
$\pi \delta \subset \alpha$
. Finally
![]() $d_{\alpha }(\pi x,\pi y)=d_{\Omega }(\pi x,\pi y)$
, which proves (i).
$d_{\alpha }(\pi x,\pi y)=d_{\Omega }(\pi x,\pi y)$
, which proves (i).
Equality implies
![]() $\alpha =\pi \delta$
. Thus, after relabelling if needed,
$\alpha =\pi \delta$
. Thus, after relabelling if needed,
![]() $b_{\pm }\in H_{\pm }$
. Thus
$b_{\pm }\in H_{\pm }$
. Thus
![]() $[a_{\pm },b_{\pm }]\subset H_{\pm }\cap \textrm {Fr}\Omega$
. If
$[a_{\pm },b_{\pm }]\subset H_{\pm }\cap \textrm {Fr}\Omega$
. If
![]() $\Omega$
is strictly convex it follows that
$\Omega$
is strictly convex it follows that
![]() $b_{\pm }=a_{\pm }$
. This gives (ii). For (iii) see [Reference Cooper, Long and TillmannCLT15, (1.7)].
$b_{\pm }=a_{\pm }$
. This gives (ii). For (iii) see [Reference Cooper, Long and TillmannCLT15, (1.7)].
A line in a projective manifold is flat connected
![]() $1$
-manifold. A projective manifold
$1$
-manifold. A projective manifold
![]() $M$
is convex if every pair of points in
$M$
is convex if every pair of points in
![]() $M$
are contained in a line. The developing map might not be injective on a lift of a line. For example, every covering space of
$M$
are contained in a line. The developing map might not be injective on a lift of a line. For example, every covering space of
![]() $\mathbb{RP}^1$
is convex. It is easy to see (cf. Figure 2) the following.
$\mathbb{RP}^1$
is convex. It is easy to see (cf. Figure 2) the following.
Proposition 1.4.
Suppose that
![]() $\Omega$
is properly convex and
$\Omega$
is properly convex and
![]() $\gamma _1,\gamma _2:[0,1)\to \Omega$
are two lines that are both contained in the same projective plane, and
$\gamma _1,\gamma _2:[0,1)\to \Omega$
are two lines that are both contained in the same projective plane, and
![]() $p_i=\lim _{t\to 1}\gamma _i(t)\in \textrm {Fr}\Omega$
. Let
$p_i=\lim _{t\to 1}\gamma _i(t)\in \textrm {Fr}\Omega$
. Let
![]() $f(t)=d_{\Omega }(\gamma _1(t),\gamma _2)$
.
$f(t)=d_{\Omega }(\gamma _1(t),\gamma _2)$
.
-
(i) If
 $p_1=p_2$
, then
$p_1=p_2$
, then
 $f$
is a non-increasing function. Moreover,
$f$
is a non-increasing function. Moreover,
 $f(t)\to 0$
if and only if
$f(t)\to 0$
if and only if
 $\Omega$
is
$\Omega$
is
 $C^1$
at
$C^1$
at
 $p_1$
.
$p_1$
. -
(ii) If
 $p_1\ne p_2$
, then
$p_1\ne p_2$
, then
 $f$
is bounded if and only if there is a segment in
$f$
is bounded if and only if there is a segment in
 $\textrm {Fr}\Omega$
that contains both
$\textrm {Fr}\Omega$
that contains both
 $p_1$
and
$p_1$
and
 $p_2$
in its interior.
$p_2$
in its interior.

Figure 2. Distance between two lines near infinity.
A subset
![]() $\mathcal{C}\subset V_0$
is a cone if
$\mathcal{C}\subset V_0$
is a cone if
![]() $t\cdot \mathcal{C}=\mathcal{C}$
for all
$t\cdot \mathcal{C}=\mathcal{C}$
for all
![]() $t\gt 0$
. The dual cone
$t\gt 0$
. The dual cone
![]() $\mathcal{C}^*=\textrm {int}\left (\{\phi \in V^*:\ \phi (\mathcal{C})\geqslant 0\}\right )$
is convex. If
$\mathcal{C}^*=\textrm {int}\left (\{\phi \in V^*:\ \phi (\mathcal{C})\geqslant 0\}\right )$
is convex. If
![]() $\Omega \subset {\mathbb{P}}_+ V$
, then
$\Omega \subset {\mathbb{P}}_+ V$
, then
![]() $\mathcal{C}\Omega$
is the cone
$\mathcal{C}\Omega$
is the cone
![]() $\{v\in V_0:\ [v]_+\in \Omega \}$
. If
$\{v\in V_0:\ [v]_+\in \Omega \}$
. If
![]() $\Omega$
is open and properly convex, then the dual domain
$\Omega$
is open and properly convex, then the dual domain
![]() $\Omega ^*={\mathbb{P}}(\mathcal{C}\Omega ^*)$
is open, and properly convex. Using the natural identification
$\Omega ^*={\mathbb{P}}(\mathcal{C}\Omega ^*)$
is open, and properly convex. Using the natural identification
![]() $V\cong V^{**}$
it is immediate that
$V\cong V^{**}$
it is immediate that
![]() $(\Omega ^*)^*=\Omega$
.
$(\Omega ^*)^*=\Omega$
.
Corollary 1.5.
If
![]() $\Omega$
is open and properly convex, then
$\Omega$
is open and properly convex, then
![]() $\Omega$
is
$\Omega$
is
![]() $C^1$
(respectively strictly convex) if and only if
$C^1$
(respectively strictly convex) if and only if
![]() $\Omega ^*$
is strictly convex (respectively
$\Omega ^*$
is strictly convex (respectively
![]() $C^1$
).
$C^1$
).
Proof.
We have
![]() $[\phi ]\in \textrm {Fr}\Omega ^*$
if and only if the dual hyperplane
$[\phi ]\in \textrm {Fr}\Omega ^*$
if and only if the dual hyperplane
![]() $H={\mathbb{P}}\ker \phi$
supports
$H={\mathbb{P}}\ker \phi$
supports
![]() $\Omega$
. In this case we will always assume that
$\Omega$
. In this case we will always assume that
![]() $\phi (\Omega )\geqslant 0$
. If
$\phi (\Omega )\geqslant 0$
. If
![]() $p\in \textrm {Fr}\Omega$
, then there are two distinct supporting hyperplanes
$p\in \textrm {Fr}\Omega$
, then there are two distinct supporting hyperplanes
![]() $H_0={\mathbb{P}}\ker \phi _0$
and
$H_0={\mathbb{P}}\ker \phi _0$
and
![]() $H_1={\mathbb{P}}\ker \phi _1$
for
$H_1={\mathbb{P}}\ker \phi _1$
for
![]() $\Omega$
at
$\Omega$
at
![]() $p$
if and only if all the hyperplanes
$p$
if and only if all the hyperplanes
![]() $H_t={\mathbb{P}}\ker \phi _t$
contain
$H_t={\mathbb{P}}\ker \phi _t$
contain
![]() $p$
and support
$p$
and support
![]() $\Omega$
, where
$\Omega$
, where
![]() $\phi _t=(1-t)\phi _0+t\phi _1$
and
$\phi _t=(1-t)\phi _0+t\phi _1$
and
![]() $0\leqslant t\leqslant 1.$
This happens if and only if the segment
$0\leqslant t\leqslant 1.$
This happens if and only if the segment
![]() $\sigma =\{[\phi _t]:\ 0\leqslant t\leqslant 1\}$
is in
$\sigma =\{[\phi _t]:\ 0\leqslant t\leqslant 1\}$
is in
![]() $\textrm {Fr}\Omega ^*$
. Hence,
$\textrm {Fr}\Omega ^*$
. Hence,
![]() $\Omega$
is
$\Omega$
is
![]() $C^1$
if and only if
$C^1$
if and only if
![]() $\Omega ^*$
is strictly convex. Replacing
$\Omega ^*$
is strictly convex. Replacing
![]() $\Omega$
by
$\Omega$
by
![]() $\Omega ^*$
and using
$\Omega ^*$
and using
![]() $\Omega ^{**}=\Omega$
gives the other result.
$\Omega ^{**}=\Omega$
gives the other result.
If
![]() $\Gamma \subset {\textrm {Aut}}(\Omega )$
is a discrete and torsion-free subgroup, then
$\Gamma \subset {\textrm {Aut}}(\Omega )$
is a discrete and torsion-free subgroup, then
![]() $M=\Omega /\Gamma$
is a properly (respectively strictly) convex manifold if
$M=\Omega /\Gamma$
is a properly (respectively strictly) convex manifold if
![]() $\Omega$
is properly (respectively strictly) convex. Then
$\Omega$
is properly (respectively strictly) convex. Then
![]() $\widetilde M=\Omega$
and there is a development pair
$\widetilde M=\Omega$
and there is a development pair
![]() $(\textrm {dev},\rho )$
, where
$(\textrm {dev},\rho )$
, where
![]() $\textrm {dev}$
is the identity map, and the holonomy
$\textrm {dev}$
is the identity map, and the holonomy
![]() $\rho :\pi _1M\to \Gamma$
is an isomorphism.
$\rho :\pi _1M\to \Gamma$
is an isomorphism.
The tautological line bundle is the quotient map
![]() $\pi :V_0\rightarrow {\mathbb{P}} V$
. If
$\pi :V_0\rightarrow {\mathbb{P}} V$
. If
![]() $M$
is a projective manifold modelled on
$M$
is a projective manifold modelled on
![]() ${\mathbb{P}} V$
, then the pull-back of this line bundle by the developing map
${\mathbb{P}} V$
, then the pull-back of this line bundle by the developing map
![]() $\textrm {dev}:\widetilde M\rightarrow {\mathbb{P}} V$
is a line bundle over
$\textrm {dev}:\widetilde M\rightarrow {\mathbb{P}} V$
is a line bundle over
![]() $\widetilde M$
. Covering transformations induce bundle isomorphisms, and the quotient is a line bundle over
$\widetilde M$
. Covering transformations induce bundle isomorphisms, and the quotient is a line bundle over
![]() $M$
called the tautological line bundle. It is a trivial bundle, since the lines can be oriented to point away from
$M$
called the tautological line bundle. It is a trivial bundle, since the lines can be oriented to point away from
![]() $0$
.
$0$
.
This bundle has a natural structure as a radiant-affine manifold. In the case that
![]() $M=\Omega /\Gamma$
is properly convex, the holonomy lifts to
$M=\Omega /\Gamma$
is properly convex, the holonomy lifts to
![]() $\widetilde \Gamma \subset \textrm {SL}_{\pm } V$
. Then this bundle over
$\widetilde \Gamma \subset \textrm {SL}_{\pm } V$
. Then this bundle over
![]() $\widetilde M$
is naturally identified with
$\widetilde M$
is naturally identified with
![]() $\mathcal{C}\Omega$
and the quotient
$\mathcal{C}\Omega$
and the quotient
![]() $\mathcal{C}\Omega /\widetilde \Gamma$
is a radiant-affine manifold (3.3) that can be naturally identified with the tautological line bundle over
$\mathcal{C}\Omega /\widetilde \Gamma$
is a radiant-affine manifold (3.3) that can be naturally identified with the tautological line bundle over
![]() $M$
. This plays a key role in the proof of the Open Theorem. If
$M$
. This plays a key role in the proof of the Open Theorem. If
![]() $X$
is a subset of a metric space
$X$
is a subset of a metric space
![]() $Y$
, the
$Y$
, the
![]() $r$
-neighborhood of
$r$
-neighborhood of
![]() $X$
is
$X$
is
We now use a compactness argument to show that if
![]() $\Omega$
is the universal cover of a closed strictly convex manifold, then projection from a projective subspace onto a geodesic in
$\Omega$
is the universal cover of a closed strictly convex manifold, then projection from a projective subspace onto a geodesic in
![]() $\Omega$
is uniformly distance decreasing in the following sense.
$\Omega$
is uniformly distance decreasing in the following sense.
Lemma 1.6.
Suppose
![]() $M=\Omega /\Gamma$
is a strictly convex closed manifold. Given
$M=\Omega /\Gamma$
is a strictly convex closed manifold. Given
![]() $b\gt 1$
there is
$b\gt 1$
there is
![]() $R=R(b)\gt 0$
so the following holds. Suppose
$R=R(b)\gt 0$
so the following holds. Suppose
![]() $\pi :\Omega \to \alpha$
is a projection onto a geodesic
$\pi :\Omega \to \alpha$
is a projection onto a geodesic
![]() $\alpha$
. Suppose that
$\alpha$
. Suppose that
![]() $\eta$
is a rectifiable arc in
$\eta$
is a rectifiable arc in
![]() $\Omega \setminus N_R(\alpha )$
of length
$\Omega \setminus N_R(\alpha )$
of length
![]() $\ell$
with endpoints
$\ell$
with endpoints
![]() $x$
and
$x$
and
![]() $y$
. Then
$y$
. Then
![]() $d_{\Omega }(\pi x,\pi y)\lt 1+(\ell /b)$
.
$d_{\Omega }(\pi x,\pi y)\lt 1+(\ell /b)$
.
Proof.
By decomposing
![]() $\eta$
into finitely many subarcs, with one of length at most
$\eta$
into finitely many subarcs, with one of length at most
![]() $b$
, and
$b$
, and
![]() $\lfloor \ell /b \rfloor$
of length
$\lfloor \ell /b \rfloor$
of length
![]() $b$
, it suffices to prove if
$b$
, it suffices to prove if
![]() ${\textrm {length}}(\eta )\leqslant b$
, then
${\textrm {length}}(\eta )\leqslant b$
, then
![]() $d_{\Omega }(\pi x,\pi y)\leqslant 1$
.
$d_{\Omega }(\pi x,\pi y)\leqslant 1$
.
Write
![]() $d=d_{\Omega }$
. If no such
$d=d_{\Omega }$
. If no such
![]() $R$
exists, then there are sequences
$R$
exists, then there are sequences
![]() $x_k,y_k\in \Omega$
and projections
$x_k,y_k\in \Omega$
and projections
![]() $\pi _{_k}:\Omega \to \alpha _k$
with
$\pi _{_k}:\Omega \to \alpha _k$
with
![]() $d(x_k,y_k)\leqslant b$
and
$d(x_k,y_k)\leqslant b$
and
![]() $d(x_k,\alpha _k)\geqslant k$
and
$d(x_k,\alpha _k)\geqslant k$
and
![]() $1\leqslant d(\pi _{_k} x_k,\pi _{_k} y_k)\leqslant b$
. Then
$1\leqslant d(\pi _{_k} x_k,\pi _{_k} y_k)\leqslant b$
. Then
![]() $\beta _k=[\pi _k x_k,x_k]$
and
$\beta _k=[\pi _k x_k,x_k]$
and
![]() $\gamma _k=[\pi _{_k} y_k,y_k]$
are geodesic segments and
$\gamma _k=[\pi _{_k} y_k,y_k]$
are geodesic segments and
![]() $\pi _{_k}\beta _k=\pi _{_k} x_k$
and
$\pi _{_k}\beta _k=\pi _{_k} x_k$
and
![]() $\pi _{_k}\gamma _k=\pi _{_k}y_k$
.
$\pi _{_k}\gamma _k=\pi _{_k}y_k$
.
There is a compact subset
![]() $W\subset \Omega$
such that
$W\subset \Omega$
such that
![]() $\Gamma \cdot W=\Omega$
. By applying an element of
$\Gamma \cdot W=\Omega$
. By applying an element of
![]() $\Gamma$
we may assume that
$\Gamma$
we may assume that
![]() $\pi _{_k}x_k\in W$
. After subsequencing we may assume
$\pi _{_k}x_k\in W$
. After subsequencing we may assume
![]() $\beta =\lim \beta _k$
,
$\beta =\lim \beta _k$
,
![]() $\gamma =\lim \gamma _k$
,
$\gamma =\lim \gamma _k$
,
![]() $\alpha =\lim \alpha _k$
and
$\alpha =\lim \alpha _k$
and
![]() $\pi =\lim \pi _{_k}$
all exist and
$\pi =\lim \pi _{_k}$
all exist and
![]() $\pi :\Omega \to \alpha$
is projection. Refer to Figure 1. Thus
$\pi :\Omega \to \alpha$
is projection. Refer to Figure 1. Thus
![]() $\beta$
are
$\beta$
are
![]() $\gamma$
are geodesic rays in
$\gamma$
are geodesic rays in
![]() $\Omega$
that start on
$\Omega$
that start on
![]() $\alpha$
, and end on
$\alpha$
, and end on
![]() $\textrm {Fr}\Omega$
, with
$\textrm {Fr}\Omega$
, with
![]() $\pi (\beta )=\alpha \cap \beta \ne \alpha \cap \gamma =\pi (\gamma )$
.
$\pi (\beta )=\alpha \cap \beta \ne \alpha \cap \gamma =\pi (\gamma )$
.
Since
![]() $\Omega$
is strictly convex, and
$\Omega$
is strictly convex, and
![]() $d(x_k,y_k)\leqslant b$
, it follows from (1.4) that
$d(x_k,y_k)\leqslant b$
, it follows from (1.4) that
![]() $x_k$
and
$x_k$
and
![]() $y_k$
limit on the same point
$y_k$
limit on the same point
![]() $p\in \textrm {Fr}\Omega$
. Hence
$p\in \textrm {Fr}\Omega$
. Hence
![]() $p$
is the endpoint of both
$p$
is the endpoint of both
![]() $\beta$
and
$\beta$
and
![]() $\gamma$
on
$\gamma$
on
![]() $\textrm {Fr}\Omega$
. Also
$\textrm {Fr}\Omega$
. Also
![]() $p\in P=H_-\cap H_+$
, where
$p\in P=H_-\cap H_+$
, where
![]() $H_{\pm }$
are the supporting hyperplanes to
$H_{\pm }$
are the supporting hyperplanes to
![]() $\Omega$
at the endpoints of
$\Omega$
at the endpoints of
![]() $\alpha$
. Since
$\alpha$
. Since
![]() $\Omega$
is strictly convex,
$\Omega$
is strictly convex,
![]() $p\notin P$
. It follows that
$p\notin P$
. It follows that
![]() $\pi (\beta )=\pi (p)=\pi (\gamma )$
which is a contradiction.
$\pi (\beta )=\pi (p)=\pi (\gamma )$
which is a contradiction.
The following is due to Benoist [Reference BenoistBen04]. A triangle is a disc
![]() $\Delta$
in a projective plane bounded by three segments. If
$\Delta$
in a projective plane bounded by three segments. If
![]() $\Delta \subset \textrm {cl}\Omega$
and
$\Delta \subset \textrm {cl}\Omega$
and
![]() $\Delta \cap \textrm {Fr}\Omega =\partial \Delta$
, then
$\Delta \cap \textrm {Fr}\Omega =\partial \Delta$
, then
![]() $\Delta$
is called a properly embedded triangle, or PET. A properly convex set
$\Delta$
is called a properly embedded triangle, or PET. A properly convex set
![]() $\Omega$
has thin triangles if there is
$\Omega$
has thin triangles if there is
![]() $\delta \gt 0$
such that for every triangle
$\delta \gt 0$
such that for every triangle
![]() $T$
in
$T$
in
![]() $\Omega$
, each side of
$\Omega$
, each side of
![]() $T$
is contained in a
$T$
is contained in a
![]() $\delta$
-neighborhood of the union of the other two sides with respect to the Hilbert metric.
$\delta$
-neighborhood of the union of the other two sides with respect to the Hilbert metric.
Proposition 1.7.
If
![]() $M=\Omega /\Gamma$
is a properly convex closed manifold, then the following are equivalent:
$M=\Omega /\Gamma$
is a properly convex closed manifold, then the following are equivalent:
-
(i)
 $M$
is strictly convex;
$M$
is strictly convex;
-
(ii)
 $\Omega$
does not contain a PET;
$\Omega$
does not contain a PET;
-
(iii)
 $\Omega$
has thin triangles.
$\Omega$
has thin triangles.
Proof.
![]() $(ii)\Rightarrow (i)$
: if
$(ii)\Rightarrow (i)$
: if
![]() $\Omega$
is not strictly convex, there is a maximal segment
$\Omega$
is not strictly convex, there is a maximal segment
![]() $\ell \subset \textrm {Fr}\Omega$
. Choose
$\ell \subset \textrm {Fr}\Omega$
. Choose
![]() $x\in \Omega$
and let
$x\in \Omega$
and let
![]() $P\subset \Omega$
be the interior of the triangle that is the convex hull of
$P\subset \Omega$
be the interior of the triangle that is the convex hull of
![]() $x$
and
$x$
and
![]() $\ell$
. Choose a sequence
$\ell$
. Choose a sequence
![]() $x_n$
in
$x_n$
in
![]() $P$
that limits on the midpoint of
$P$
that limits on the midpoint of
![]() $\ell$
. By (1.4)
$\ell$
. By (1.4)
![]() $d_{\Omega }(x_n,\textrm {Fr} P)\to \infty$
because
$d_{\Omega }(x_n,\textrm {Fr} P)\to \infty$
because
![]() $\ell$
is maximal. Since
$\ell$
is maximal. Since
![]() $M$
is compact there is compact set
$M$
is compact there is compact set
![]() $W\subset \Omega$
such that
$W\subset \Omega$
such that
![]() $\Gamma \cdot W=\Omega$
. Thus there is
$\Gamma \cdot W=\Omega$
. Thus there is
![]() $\gamma _n\in \Gamma$
with
$\gamma _n\in \Gamma$
with
![]() $\gamma _nx_n\in W$
. After choosing a subsequence
$\gamma _nx_n\in W$
. After choosing a subsequence
![]() $\gamma _nx_n\to y\in W$
, and
$\gamma _nx_n\to y\in W$
, and
![]() $\gamma _n P$
converges to the interior of a PET
$\gamma _n P$
converges to the interior of a PET
![]() $\Delta \subset \Omega$
that contains
$\Delta \subset \Omega$
that contains
![]() $y$
.
$y$
.
![]() $(iii)\Rightarrow (ii)$
: if
$(iii)\Rightarrow (ii)$
: if
![]() $\Omega$
contains a PET
$\Omega$
contains a PET
![]() $\Delta$
, then
$\Delta$
, then
![]() $d_{\Omega }|\Delta =d_{\Delta }.$
Now
$d_{\Omega }|\Delta =d_{\Delta }.$
Now
![]() $\textrm {PGL}(\Delta )$
contains a subgroup
$\textrm {PGL}(\Delta )$
contains a subgroup
![]() $G\cong {\mathbb{R}}^2$
that acts transitively on
$G\cong {\mathbb{R}}^2$
that acts transitively on
![]() $\Delta$
. Therefore
$\Delta$
. Therefore
![]() $(\Delta ,d_{\Delta })$
is isometric to a normed vector-space, thus does not have thin triangles.
$(\Delta ,d_{\Delta })$
is isometric to a normed vector-space, thus does not have thin triangles.
![]() $(i)\Rightarrow (iii)$
: if
$(i)\Rightarrow (iii)$
: if
![]() $\Omega$
does not have thin triangles, then there is a sequence of triangles
$\Omega$
does not have thin triangles, then there is a sequence of triangles
![]() $T_k$
in
$T_k$
in
![]() $\Omega$
and points
$\Omega$
and points
![]() $x_k$
in
$x_k$
in
![]() $T_k$
with
$T_k$
with
![]() $d_{\Omega }(x_k,\partial T_k)\gt k$
. As above, after applying elements of
$d_{\Omega }(x_k,\partial T_k)\gt k$
. As above, after applying elements of
![]() $\Gamma$
, we may assume
$\Gamma$
, we may assume
![]() $T_k$
converges to a PET, so
$T_k$
converges to a PET, so
![]() $\Omega$
is not strictly convex.
$\Omega$
is not strictly convex.
It follows that in dimension
![]() $2$
either
$2$
either
![]() $\Omega$
is a triangle (and
$\Omega$
is a triangle (and
![]() $M$
is a torus or Klein bottle) or else is strictly convex. Using a basic fact from geometric group theory, it follows that a properly convex manifold (of any dimension) is strictly convex if and only if
$M$
is a torus or Klein bottle) or else is strictly convex. Using a basic fact from geometric group theory, it follows that a properly convex manifold (of any dimension) is strictly convex if and only if
![]() $\pi _1M$
has thin triangles. This is an algebraic characterization of strictly convex. However, we will give a direct geometric argument.
$\pi _1M$
has thin triangles. This is an algebraic characterization of strictly convex. However, we will give a direct geometric argument.
Given
![]() $K\geqslant 1$
and
$K\geqslant 1$
and
![]() $L\geqslant 0$
, a
$L\geqslant 0$
, a
![]() $(K,L)$
-quasi-isometric embedding is a map
$(K,L)$
-quasi-isometric embedding is a map
![]() $f:X\to Y$
between metric spaces
$f:X\to Y$
between metric spaces
![]() $(X,d_X)$
and
$(X,d_X)$
and
![]() $(Y,d_Y)$
such that
$(Y,d_Y)$
such that
for all
![]() $x,x^{\prime}\in X.$
If
$x,x^{\prime}\in X.$
If
![]() $X=[a,b]\subset {\mathbb{R}}$
, then
$X=[a,b]\subset {\mathbb{R}}$
, then
![]() $f$
is a quasi-geodesic. The map
$f$
is a quasi-geodesic. The map
![]() $f$
is a quasi-isometry, or QI, if also
$f$
is a quasi-isometry, or QI, if also
![]() $Y\subset N(fX,L)$
.
$Y\subset N(fX,L)$
.
If
![]() $g:Y\to Z$
is a
$g:Y\to Z$
is a
![]() $(K^{\prime},L^{\prime})$
-QI, then
$(K^{\prime},L^{\prime})$
-QI, then
![]() $g\circ f$
is a
$g\circ f$
is a
![]() $(KK^{\prime},K^{\prime}L+L^{\prime})$
-QI. In particular, if
$(KK^{\prime},K^{\prime}L+L^{\prime})$
-QI. In particular, if
![]() $g$
is a QI and
$g$
is a QI and
![]() $f$
is a quasi-geodesic, then
$f$
is a quasi-geodesic, then
![]() $g\circ f$
is a quasi-geodesic with QI constants that only depend on those of
$g\circ f$
is a quasi-geodesic with QI constants that only depend on those of
![]() $f$
and
$f$
and
![]() $g$
.
$g$
.
If
![]() $G$
is a finitely generated group, then a choice of finite generating set gives a word metric on
$G$
is a finitely generated group, then a choice of finite generating set gives a word metric on
![]() $G$
. A different choice of generating set gives a bi-Lipschitz equivalent metric. The Švarc–Milnor lemma in this setting is
$G$
. A different choice of generating set gives a bi-Lipschitz equivalent metric. The Švarc–Milnor lemma in this setting is
Proposition 1.8.
If
![]() $M=\Omega /\Gamma$
is a closed and properly convex manifold, then
$M=\Omega /\Gamma$
is a closed and properly convex manifold, then
![]() $(\Omega ,d_{\Omega })$
is QI to
$(\Omega ,d_{\Omega })$
is QI to
![]() $\pi _1M$
.
$\pi _1M$
.
Proof.
Fix
![]() $x\in \widetilde M=\Omega$
. Then
$x\in \widetilde M=\Omega$
. Then
![]() $f:\pi _1M\rightarrow \widetilde M$
given by
$f:\pi _1M\rightarrow \widetilde M$
given by
![]() $f(g)=\tau _g(x)$
is a QI.
$f(g)=\tau _g(x)$
is a QI.
A metric space
![]() $(Y,d_Y)$
is ML if it satisfies the Morse Lemma, i.e. for all
$(Y,d_Y)$
is ML if it satisfies the Morse Lemma, i.e. for all
![]() $(K,L)$
there is
$(K,L)$
there is
![]() $S=S(K,L)\gt 0$
, called a tracking constant, such that if
$S=S(K,L)\gt 0$
, called a tracking constant, such that if
![]() $\alpha$
and
$\alpha$
and
![]() $\beta$
are
$\beta$
are
![]() $(K,L)$
-quasi-geodesics in
$(K,L)$
-quasi-geodesics in
![]() $Y$
with the same endpoints, then
$Y$
with the same endpoints, then
![]() $\alpha \subset N_{S}(\beta )$
and
$\alpha \subset N_{S}(\beta )$
and
![]() $\beta \subset N_{S}(\alpha )$
. Since quasi-geodesics are sent to quasi-geodesics by quasi-isometries, it follows that the property of ML is preserved by QI.
$\beta \subset N_{S}(\alpha )$
. Since quasi-geodesics are sent to quasi-geodesics by quasi-isometries, it follows that the property of ML is preserved by QI.
Clearly
![]() ${\mathbb{R}}^2$
is not ML, and any norm on
${\mathbb{R}}^2$
is not ML, and any norm on
![]() ${\mathbb{R}}^2$
is QI to the standard norm, so
${\mathbb{R}}^2$
is QI to the standard norm, so
![]() ${\mathbb{R}}^2$
with any norm is not ML. A geodesic in the Cayley graph of
${\mathbb{R}}^2$
with any norm is not ML. A geodesic in the Cayley graph of
![]() $G$
picks out a sequence in
$G$
picks out a sequence in
![]() $G$
that is a quasi-geodesic. It follows from (1.8) that whether or not a closed properly convex manifold is ML only depends on
$G$
that is a quasi-geodesic. It follows from (1.8) that whether or not a closed properly convex manifold is ML only depends on
![]() $\pi _1M$
.
$\pi _1M$
.
Proposition 1.9.
If
![]() $M=\Omega /\Gamma$
is a properly convex closed manifold, then
$M=\Omega /\Gamma$
is a properly convex closed manifold, then
![]() $M$
is strictly convex if and only if
$M$
is strictly convex if and only if
![]() $(\Omega ,d_{\Omega })$
is ML.
$(\Omega ,d_{\Omega })$
is ML.
Proof.
If
![]() $\Omega$
is not strictly convex, then by (1.7) it contains a PET
$\Omega$
is not strictly convex, then by (1.7) it contains a PET
![]() $\Delta$
. The metric
$\Delta$
. The metric
![]() $d_{\Omega }$
restricted to
$d_{\Omega }$
restricted to
![]() $\Delta$
is isometric to a norm on
$\Delta$
is isometric to a norm on
![]() ${\mathbb{R}}^2$
. Hence,
${\mathbb{R}}^2$
. Hence,
![]() $(\Omega ,d_{\Omega })$
is not ML.
$(\Omega ,d_{\Omega })$
is not ML.

Figure 3. Quasi-geodesics.
Now suppose
![]() $\Omega$
is strictly convex. A quasi-geodesic is nice if the image consists of finitely many line segments and each line segment is parameterized by arc length. Every
$\Omega$
is strictly convex. A quasi-geodesic is nice if the image consists of finitely many line segments and each line segment is parameterized by arc length. Every
![]() $(K,L)$
-quasi-geodesic
$(K,L)$
-quasi-geodesic
![]() $\alpha$
in
$\alpha$
in
![]() $\Omega$
is approximated by a nice
$\Omega$
is approximated by a nice
![]() $(K^{\prime},L^{\prime})$
-quasi-geodesic
$(K^{\prime},L^{\prime})$
-quasi-geodesic
![]() $\overline {\alpha }$
in the sense that
$\overline {\alpha }$
in the sense that
![]() $\alpha \subset N(\overline {\alpha },D)$
and
$\alpha \subset N(\overline {\alpha },D)$
and
![]() $\overline {\alpha }\subset N(\alpha ,D)$
and
$\overline {\alpha }\subset N(\alpha ,D)$
and
![]() $(D, K^{\prime},L^{\prime})$
only depends on
$(D, K^{\prime},L^{\prime})$
only depends on
![]() $(K,L)$
. Thus it suffices to prove there is a tracking constant for nice quasi-geodesics.
$(K,L)$
. Thus it suffices to prove there is a tracking constant for nice quasi-geodesics.
Refer to Figure 3. Let
![]() $\alpha ^{\prime}$
be a nice
$\alpha ^{\prime}$
be a nice
![]() $(K,L)$
-quasi-geodesic with endpoints
$(K,L)$
-quasi-geodesic with endpoints
![]() $p$
and
$p$
and
![]() $q$
. Let
$q$
. Let
![]() $\beta ^{\prime}$
be the line segment with the same endpoints as
$\beta ^{\prime}$
be the line segment with the same endpoints as
![]() $\alpha ^{\prime}$
. Let
$\alpha ^{\prime}$
. Let
![]() $R=R(2K)$
be given by (1.6) and set
$R=R(2K)$
be given by (1.6) and set
![]() $S^{\prime}=R+4RK+K+L$
. We show that
$S^{\prime}=R+4RK+K+L$
. We show that
![]() $S=2KS^{\prime}+2L+2S^{\prime}$
is a tracking constant. Let
$S=2KS^{\prime}+2L+2S^{\prime}$
is a tracking constant. Let
![]() $\beta ^+$
be the geodesic in
$\beta ^+$
be the geodesic in
![]() $\Omega$
that contains
$\Omega$
that contains
![]() $\beta ^{\prime}$
and
$\beta ^{\prime}$
and
![]() $\pi :\Omega \rightarrow \beta ^+$
be a projection.
$\pi :\Omega \rightarrow \beta ^+$
be a projection.
Claim 1:
![]() $\alpha ^{\prime}\subset N(\beta ^+,S^{\prime})$
.
$\alpha ^{\prime}\subset N(\beta ^+,S^{\prime})$
.
Claim 2:
![]() $\alpha ^{\prime}\subset N(\beta ^{\prime},S/2)$
and
$\alpha ^{\prime}\subset N(\beta ^{\prime},S/2)$
and
![]() $\beta ^{\prime}\subset N(\alpha ^{\prime},S/2)$
.
$\beta ^{\prime}\subset N(\alpha ^{\prime},S/2)$
.
Assuming the claims, if
![]() $\gamma ^{\prime}$
is another nice
$\gamma ^{\prime}$
is another nice
![]() $(K,L)$
-quasi-geodesic with endpoints
$(K,L)$
-quasi-geodesic with endpoints
![]() $p$
and
$p$
and
![]() $q$
, then
$q$
, then
which proves that
![]() $S$
is a tracking constant. Hence,
$S$
is a tracking constant. Hence,
![]() $(\Omega ,d_{\Omega })$
is ML.
$(\Omega ,d_{\Omega })$
is ML.
For Claim 1, suppose that
![]() $\alpha$
is the closure of a component of
$\alpha$
is the closure of a component of
![]() $\alpha ^{\prime}\setminus N(\beta ^+,R)$
. The endpoints
$\alpha ^{\prime}\setminus N(\beta ^+,R)$
. The endpoints
![]() $x$
and
$x$
and
![]() $y$
of
$y$
of
![]() $\alpha$
satisfy
$\alpha$
satisfy
![]() $d(x,\beta ^+)=d(y,\beta ^+)=R$
. Let
$d(x,\beta ^+)=d(y,\beta ^+)=R$
. Let
![]() $x^{\prime},y^{\prime}\in \beta ^+$
be chosen so that
$x^{\prime},y^{\prime}\in \beta ^+$
be chosen so that
![]() $d(x,x^{\prime})=R=d(y,y^{\prime})$
and let
$d(x,x^{\prime})=R=d(y,y^{\prime})$
and let
![]() $\beta =[\pi x,\pi y]\subset \beta ^+$
. By (1.6),
$\beta =[\pi x,\pi y]\subset \beta ^+$
. By (1.6),
by definition of
![]() $R$
. Since
$R$
. Since
![]() $\pi$
is distance non-increasing
$\pi$
is distance non-increasing
![]() $d(x^{\prime},\pi x)=d(\pi x^{\prime},\pi x)\leqslant d(x^{\prime}, x)=R$
, and similarly
$d(x^{\prime},\pi x)=d(\pi x^{\prime},\pi x)\leqslant d(x^{\prime}, x)=R$
, and similarly
![]() $d(y^{\prime},\pi y)\leqslant R$
. Thus
$d(y^{\prime},\pi y)\leqslant R$
. Thus
Since
![]() $\alpha$
is parametrized by arc length, the domain of
$\alpha$
is parametrized by arc length, the domain of
![]() $\alpha$
is
$\alpha$
is
![]() ${\textrm {length}}(\alpha )$
, Since
${\textrm {length}}(\alpha )$
, Since
![]() $\alpha$
is a
$\alpha$
is a
![]() $(K,L)$
-quasi-geodesic, we have
$(K,L)$
-quasi-geodesic, we have
 \begin{equation*}\begin{array}{lrcl} & K^{-1}({\textrm {length}}(\alpha )-L)& \leqslant & d(x,y)\\ \Rightarrow & {\textrm {length}}(\alpha ) &\leqslant & K\cdot d(x,y)+L \\ & & \leqslant & K(4R +{\textrm {length}}(\beta ))+L\\ & & \leqslant & K(4R+1+{\textrm {length}}(\alpha )/2K)+L\\ & & = &4RK+K+L+{\textrm {length}}(\alpha )/2\\ \Rightarrow & (1/2){\textrm {length}}(\alpha )&\leqslant & 4RK+K+L. \end{array}\end{equation*}
\begin{equation*}\begin{array}{lrcl} & K^{-1}({\textrm {length}}(\alpha )-L)& \leqslant & d(x,y)\\ \Rightarrow & {\textrm {length}}(\alpha ) &\leqslant & K\cdot d(x,y)+L \\ & & \leqslant & K(4R +{\textrm {length}}(\beta ))+L\\ & & \leqslant & K(4R+1+{\textrm {length}}(\alpha )/2K)+L\\ & & = &4RK+K+L+{\textrm {length}}(\alpha )/2\\ \Rightarrow & (1/2){\textrm {length}}(\alpha )&\leqslant & 4RK+K+L. \end{array}\end{equation*}
Since the endpoints of
![]() $\alpha$
are in
$\alpha$
are in
![]() $N(\beta ^+,R)$
, it follows that
$N(\beta ^+,R)$
, it follows that
Now
This proves Claim 1.
For Claim 2, let
![]() $\Pi :\alpha ^{\prime}\rightarrow \beta ^+$
be the nearest point retraction. This map is continuous, and
$\Pi :\alpha ^{\prime}\rightarrow \beta ^+$
be the nearest point retraction. This map is continuous, and
![]() $p,q$
are both in the image, so the image of
$p,q$
are both in the image, so the image of
![]() $\Pi \circ \alpha ^{\prime}$
contains
$\Pi \circ \alpha ^{\prime}$
contains
![]() $\beta ^{\prime}$
. If
$\beta ^{\prime}$
. If
![]() $x^{\prime}\in \beta ^{\prime}$
there is
$x^{\prime}\in \beta ^{\prime}$
there is
![]() $y^{\prime}\in \alpha ^{\prime}$
with
$y^{\prime}\in \alpha ^{\prime}$
with
![]() $\Pi y^{\prime}=x^{\prime}$
. Then
$\Pi y^{\prime}=x^{\prime}$
. Then
![]() $d(\beta ^+,y^{\prime})=d(x^{\prime},y^{\prime})$
, and by Claim 1
$d(\beta ^+,y^{\prime})=d(x^{\prime},y^{\prime})$
, and by Claim 1
![]() $d(\beta ^+,y^{\prime})\leqslant S^{\prime}$
so
$d(\beta ^+,y^{\prime})\leqslant S^{\prime}$
so
![]() $d(x^{\prime},y^{\prime})\leqslant S^{\prime}$
thus
$d(x^{\prime},y^{\prime})\leqslant S^{\prime}$
thus
Let
![]() $\delta \subset \alpha ^{\prime}$
be the closure of a component of
$\delta \subset \alpha ^{\prime}$
be the closure of a component of
![]() $\alpha ^{\prime}\setminus \eta$
, thus
$\alpha ^{\prime}\setminus \eta$
, thus
![]() $\delta$
is an arc in the interior of
$\delta$
is an arc in the interior of
![]() $\alpha ^{\prime}$
. Let
$\alpha ^{\prime}$
. Let
![]() $r,s$
be the endpoints of
$r,s$
be the endpoints of
![]() $\delta$
. Then
$\delta$
. Then
![]() $\Pi (r)=\Pi (s)\in \{p,q\}$
. By Claim 1,
$\Pi (r)=\Pi (s)\in \{p,q\}$
. By Claim 1,
Since
![]() $\delta$
is a nice
$\delta$
is a nice
![]() $(K,L)$
-quasi-geodesic,
$(K,L)$
-quasi-geodesic,
By Claim 1, the endpoints of
![]() $\delta$
are distance at most
$\delta$
are distance at most
![]() $S^{\prime}$
from
$S^{\prime}$
from
![]() $\beta ^{\prime}$
so
$\beta ^{\prime}$
so
Since
![]() $\delta \cup \eta \subset N(\beta ^{\prime},S/2)$
it follows that
$\delta \cup \eta \subset N(\beta ^{\prime},S/2)$
it follows that
![]() $\alpha ^{\prime}\subset N(\beta ^{\prime},S/2)$
, proving Claim 2.
$\alpha ^{\prime}\subset N(\beta ^{\prime},S/2)$
, proving Claim 2.
In the proof of the Closed Theorem, we construct a properly convex manifold with the correct holonomy. In order to know this manifold is closed and strictly convex we use the pair of results (1.10) and (1.11). A properly convex manifold has contractible universal cover. Whitehead’s theorem (that a weak homotopy equivalence between CW complexes is a homotopy equivalence) implies that if
![]() $M$
and
$M$
and
![]() $M^{\prime}$
are properly convex and
$M^{\prime}$
are properly convex and
![]() $\pi _1M\cong \pi _1M^{\prime}$
, then
$\pi _1M\cong \pi _1M^{\prime}$
, then
![]() $M$
and
$M$
and
![]() $M^{\prime}$
are homotopy equivalent. This is key in the following result.
$M^{\prime}$
are homotopy equivalent. This is key in the following result.
Lemma 1.10.
Suppose
![]() $M$
and
$M$
and
![]() $M^{\prime}$
are properly convex manifolds and
$M^{\prime}$
are properly convex manifolds and
![]() $\pi _1M\cong \pi _1M^{\prime}$
. If
$\pi _1M\cong \pi _1M^{\prime}$
. If
![]() $M$
is closed, then
$M$
is closed, then
![]() $M^{\prime}$
is closed.
$M^{\prime}$
is closed.
Proof.
Let
![]() $\pi :\Omega \to M$
be the projection. This is the universal covering space of
$\pi :\Omega \to M$
be the projection. This is the universal covering space of
![]() $M$
, so
$M$
, so
![]() $M$
is a
$M$
is a
![]() $K(\pi _1M,1)$
. The same holds for
$K(\pi _1M,1)$
. The same holds for
![]() $M^{\prime}$
. Hence
$M^{\prime}$
. Hence
![]() $M$
and
$M$
and
![]() $M^{\prime}$
are homotopy equivalent. If
$M^{\prime}$
are homotopy equivalent. If
![]() $n=\dim M$
, then
$n=\dim M$
, then
![]() $M$
is closed if and only if
$M$
is closed if and only if
![]() $H_n(M;{\mathbb{Z}}_2)\cong {\mathbb{Z}}_2$
. Since homology is an invariant of homotopy type the result follows.
$H_n(M;{\mathbb{Z}}_2)\cong {\mathbb{Z}}_2$
. Since homology is an invariant of homotopy type the result follows.
Corollary 1.11.
Suppose
![]() $M$
and
$M$
and
![]() $N$
are closed and properly convex, and that
$N$
are closed and properly convex, and that
![]() $\pi _1M\cong \pi _1N$
. If
$\pi _1M\cong \pi _1N$
. If
![]() $M$
is strictly convex, then
$M$
is strictly convex, then
![]() $N$
is strictly convex.
$N$
is strictly convex.
Proof.
Since ML is preserved by QI, it follows from (1.9) and (1.8) that
![]() $M$
is strictly convex if and only if
$M$
is strictly convex if and only if
![]() $\pi _1M$
is ML, and this is determined by
$\pi _1M$
is ML, and this is determined by
![]() $\pi _1M$
.
$\pi _1M$
.
The remaining discussion in this sections comes logically after Section 2 since it depends on (2.6), but it fits better into the narrative here. We let the reader choose their preferred order.
The displacement distance of
![]() $\gamma \in {\textrm {Aut}}(\Omega )$
is
$\gamma \in {\textrm {Aut}}(\Omega )$
is
![]() $t(\gamma )=\inf \{d_{\Omega }(x,\gamma x): x\in \Omega \}$
. The element
$t(\gamma )=\inf \{d_{\Omega }(x,\gamma x): x\in \Omega \}$
. The element
![]() $\gamma$
is called hyperbolic if
$\gamma$
is called hyperbolic if
![]() $t(\gamma )\gt 0$
. It is elliptic if it fixes a point in
$t(\gamma )\gt 0$
. It is elliptic if it fixes a point in
![]() $\Omega$
and parabolic if it has no fixed point in
$\Omega$
and parabolic if it has no fixed point in
![]() $\Omega$
but
$\Omega$
but
![]() $t(\gamma )=0$
. By [Reference Cooper, Long and TillmannCLT15, Proposition 2.1] we have that
$t(\gamma )=0$
. By [Reference Cooper, Long and TillmannCLT15, Proposition 2.1] we have that
![]() $t(\gamma )=\log |\lambda /\mu |$
, where
$t(\gamma )=\log |\lambda /\mu |$
, where
![]() $\lambda$
and
$\lambda$
and
![]() $\mu$
are the eigenvalues of
$\mu$
are the eigenvalues of
![]() $t(\gamma )$
of largest and smallest modulus. We will not make use of elliptics or parabolics in this paper.
$t(\gamma )$
of largest and smallest modulus. We will not make use of elliptics or parabolics in this paper.
Lemma 1.12 (Hyperbolics). Suppose
![]() $\Omega \subset {\mathbb{P}} V$
and
$\Omega \subset {\mathbb{P}} V$
and
![]() $M=\Omega /\Gamma$
is a strictly convex closed manifold and
$M=\Omega /\Gamma$
is a strictly convex closed manifold and
![]() $1\ne \gamma \in \Gamma$
. Then
$1\ne \gamma \in \Gamma$
. Then
![]() $\gamma$
is hyperbolic and there are
$\gamma$
is hyperbolic and there are
![]() $a_{\pm }\in \textrm {Fr}(\Omega )$
such that for all
$a_{\pm }\in \textrm {Fr}(\Omega )$
such that for all
![]() $x\in {\mathbb{P}} V\setminus (H_+\cup H_-)$
we have
$x\in {\mathbb{P}} V\setminus (H_+\cup H_-)$
we have
where
![]() $H_{\pm }$
is the supporting hyperplane to
$H_{\pm }$
is the supporting hyperplane to
![]() $\Omega$
at
$\Omega$
at
![]() $a_{\pm }$
.
$a_{\pm }$
.
Proof.
Since
![]() $M$
is compact, the Arzela–Ascoli Theorem implies there is a closed geodesic
$M$
is compact, the Arzela–Ascoli Theorem implies there is a closed geodesic
![]() $C$
in
$C$
in
![]() $M$
that is conjugate to
$M$
that is conjugate to
![]() $\gamma$
in
$\gamma$
in
![]() $\pi _1M$
and
$\pi _1M$
and
![]() $t(\gamma )={\textrm {length}}(C)\gt 0$
. Hence,
$t(\gamma )={\textrm {length}}(C)\gt 0$
. Hence,
![]() $\gamma$
is hyperbolic. By (1.3),
$\gamma$
is hyperbolic. By (1.3),
![]() $C$
is covered by a proper segment
$C$
is covered by a proper segment
![]() $\alpha =(a_-,a_+)$
in
$\alpha =(a_-,a_+)$
in
![]() $\Omega$
that is preserved by
$\Omega$
that is preserved by
![]() $\gamma$
. By (2.6),
$\gamma$
. By (2.6),
![]() $M$
is
$M$
is
![]() $C^1$
so there are unique supporting hyperplanes
$C^1$
so there are unique supporting hyperplanes
![]() $H_{\pm }$
to
$H_{\pm }$
to
![]() $\textrm {cl}\Omega$
that contain
$\textrm {cl}\Omega$
that contain
![]() $a_{\pm }$
, respectively. Then
$a_{\pm }$
, respectively. Then
![]() $Q=H_+\cap H_-$
is a codimension-2 subspace, and it is disjoint from
$Q=H_+\cap H_-$
is a codimension-2 subspace, and it is disjoint from
![]() $\Omega$
by strict convexity. Moreover
$\Omega$
by strict convexity. Moreover
![]() $Q$
is preserved by
$Q$
is preserved by
![]() $\gamma$
.
$\gamma$
.
The pencil of hyperplanes
![]() $\{H_t:t\in L\}$
in
$\{H_t:t\in L\}$
in
![]() ${\mathbb{P}} V$
that contain
${\mathbb{P}} V$
that contain
![]() $Q$
is dual to a line
$Q$
is dual to a line
![]() $L\subset {\mathbb{P}}(V^*)$
. Since the dual of
$L\subset {\mathbb{P}}(V^*)$
. Since the dual of
![]() $\gamma$
acts on
$\gamma$
acts on
![]() $L\cong \mathbb{RP}^1$
projectively and non-trivially, it only fixes the two points
$L\cong \mathbb{RP}^1$
projectively and non-trivially, it only fixes the two points
![]() $[H_{\pm }]\in L$
. The other hyperplanes
$[H_{\pm }]\in L$
. The other hyperplanes
![]() $[H_t]$
are moved by
$[H_t]$
are moved by
![]() $\gamma$
away from
$\gamma$
away from
![]() $[H_-]$
and towards
$[H_-]$
and towards
![]() $[H_+]$
. Since
$[H_+]$
. Since
![]() $\Omega$
is strictly convex,
$\Omega$
is strictly convex,
![]() $\gamma$
moves all points in
$\gamma$
moves all points in
![]() $\Omega$
towards
$\Omega$
towards
![]() $a_+$
. Suppose
$a_+$
. Suppose
![]() $\ell$
is a projective line that contains
$\ell$
is a projective line that contains
![]() $a_-$
. If
$a_-$
. If
![]() $\ell$
is not contained in
$\ell$
is not contained in
![]() $H_-$
, then, since
$H_-$
, then, since
![]() $H_-$
is the unique supporting hyperplane at
$H_-$
is the unique supporting hyperplane at
![]() $a_-$
, it follows that
$a_-$
, it follows that
![]() $\Omega \cap \ell \ne \emptyset$
. Thus
$\Omega \cap \ell \ne \emptyset$
. Thus
![]() $\gamma ^k\ell \to \ell ^{\prime}$
where
$\gamma ^k\ell \to \ell ^{\prime}$
where
![]() $\ell ^{\prime}$
is the projective line containing
$\ell ^{\prime}$
is the projective line containing
![]() $\alpha$
. Hence
$\alpha$
. Hence
![]() $\gamma ^k(\ell \setminus a_-)\to a_+$
as
$\gamma ^k(\ell \setminus a_-)\to a_+$
as
![]() $k\to \infty$
. This reasoning applied to
$k\to \infty$
. This reasoning applied to
![]() $\gamma ^{-1}$
gives the corresponding statements for
$\gamma ^{-1}$
gives the corresponding statements for
![]() $a_-$
, and gives the second conclusion.
$a_-$
, and gives the second conclusion.
The point
![]() $a_+$
is called the attracting, and
$a_+$
is called the attracting, and
![]() $a_-$
is the repelling, fixed point of
$a_-$
is the repelling, fixed point of
![]() $\gamma$
, and
$\gamma$
, and
![]() $(a_-,a_+)\subset \Omega$
is called the axis of
$(a_-,a_+)\subset \Omega$
is called the axis of
![]() $\gamma$
. This axis is the only proper segment in
$\gamma$
. This axis is the only proper segment in
![]() $\Omega$
preserved by
$\Omega$
preserved by
![]() $\gamma$
. The attracting fixed point of
$\gamma$
. The attracting fixed point of
![]() $\gamma ^{-1}$
is the repelling fixed point of
$\gamma ^{-1}$
is the repelling fixed point of
![]() $\gamma$
. The following result is used in our proof of Chuckrow’s theorem, that is needed for the Closed Theorem.
$\gamma$
. The following result is used in our proof of Chuckrow’s theorem, that is needed for the Closed Theorem.
Corollary 1.13 (nilpotent subgroups). If
![]() $M=\Omega /\Gamma$
is a closed, strictly convex, projective manifold, then every nilpotent subgroup of
$M=\Omega /\Gamma$
is a closed, strictly convex, projective manifold, then every nilpotent subgroup of
![]() $\Gamma$
is cyclic.
$\Gamma$
is cyclic.
Proof.
By (1.12) every element of
![]() $\Gamma$
is hyperbolic, and the axis is the only segment preserved by a non-trivial hyperbolic in
$\Gamma$
is hyperbolic, and the axis is the only segment preserved by a non-trivial hyperbolic in
![]() $\Gamma$
. If
$\Gamma$
. If
![]() $\Gamma ^{\prime}\subset \Gamma$
is nilpotent then
$\Gamma ^{\prime}\subset \Gamma$
is nilpotent then
![]() $\Gamma ^{\prime}$
has a non-trivial center. Let
$\Gamma ^{\prime}$
has a non-trivial center. Let
![]() $\beta$
be a non-trivial element of this center, and let
$\beta$
be a non-trivial element of this center, and let
![]() $\ell$
be the axis of
$\ell$
be the axis of
![]() $\beta$
. Since every element of
$\beta$
. Since every element of
![]() $\Gamma ^{\prime}$
commutes with
$\Gamma ^{\prime}$
commutes with
![]() $\beta$
it follows that
$\beta$
it follows that
![]() $\Gamma ^{\prime}$
preserves the axis of
$\Gamma ^{\prime}$
preserves the axis of
![]() $\ell$
. The action of
$\ell$
. The action of
![]() $\Gamma$
on
$\Gamma$
on
![]() $\Omega$
is free, so
$\Omega$
is free, so
![]() $\Gamma ^{\prime}$
acts freely on
$\Gamma ^{\prime}$
acts freely on
![]() $\ell$
. A discrete group acting freely by homeomorphisms on
$\ell$
. A discrete group acting freely by homeomorphisms on
![]() $\mathbb{R}$
is cyclic.
$\mathbb{R}$
is cyclic.
Two projective structures on the same manifold are equivalent if there is a projective isomorphism of one onto the other that is homotopic to the identity (rather than isotopic to the identity). For closed hyperbolic manifolds of dimension at most
![]() $3$
, homotopy implies isotopy [Reference EpsteinEps66, Reference GabaiGab01]. The next two results imply that the holonomy of a strictly convex manifold determines the domain
$3$
, homotopy implies isotopy [Reference EpsteinEps66, Reference GabaiGab01]. The next two results imply that the holonomy of a strictly convex manifold determines the domain
![]() $\Omega$
, and hence determines the projective structure, up to equivalence. However, given the holonomy, there may be two developing maps that are homotopic but not isotopic. Thus the space of equivalence classes of strictly convex projective structures on a closed manifold can be identified with a subset of the space of representations modulo conjugacy.
$\Omega$
, and hence determines the projective structure, up to equivalence. However, given the holonomy, there may be two developing maps that are homotopic but not isotopic. Thus the space of equivalence classes of strictly convex projective structures on a closed manifold can be identified with a subset of the space of representations modulo conjugacy.
Lemma 1.14.
If
![]() $M=\Omega /\Gamma$
is a closed properly convex manifold and
$M=\Omega /\Gamma$
is a closed properly convex manifold and
![]() $\Omega ^{\prime}\subset \Omega$
is a non-empty properly convex subset that is preserved by
$\Omega ^{\prime}\subset \Omega$
is a non-empty properly convex subset that is preserved by
![]() $\Gamma$
, then
$\Gamma$
, then
![]() $\Omega ^{\prime}=\Omega$
.
$\Omega ^{\prime}=\Omega$
.
Proof.
Otherwise the function
![]() $F:\Omega \to {\mathbb{R}}$
given by
$F:\Omega \to {\mathbb{R}}$
given by
![]() $F(x)=d_{\Omega }(x,\Omega ^{\prime})$
is continuous, unbounded and
$F(x)=d_{\Omega }(x,\Omega ^{\prime})$
is continuous, unbounded and
![]() $\Gamma$
-invariant. Thus it covers a continuous unbounded function
$\Gamma$
-invariant. Thus it covers a continuous unbounded function
![]() $f:M\to {\mathbb{R}}$
, contradicting the compactness of
$f:M\to {\mathbb{R}}$
, contradicting the compactness of
![]() $M$
.
$M$
.
Proposition 1.15 (Unique domain). Let
![]() $n\geqslant 2.$
Suppose
$n\geqslant 2.$
Suppose
![]() $\Omega \subset \mathbb{RP}^n$
and
$\Omega \subset \mathbb{RP}^n$
and
![]() $M=\Omega /\Gamma$
is a strictly convex, closed
$M=\Omega /\Gamma$
is a strictly convex, closed
![]() $n$
-manifold. If
$n$
-manifold. If
![]() $\Omega ^{\prime}$
is open and properly convex and preserved by
$\Omega ^{\prime}$
is open and properly convex and preserved by
![]() $\Gamma$
, then
$\Gamma$
, then
![]() $\Omega ^{\prime}=\Omega$
.
$\Omega ^{\prime}=\Omega$
.
Proof.
Let
![]() $X$
be union, over all
$X$
be union, over all
![]() $1\ne \gamma \in \Gamma$
, of attracting fixed points of
$1\ne \gamma \in \Gamma$
, of attracting fixed points of
![]() $\gamma$
. Then
$\gamma$
. Then
![]() $X\subset \textrm {Fr}\Omega$
by (1.12). Let
$X\subset \textrm {Fr}\Omega$
by (1.12). Let
![]() $W$
be the convex hull of
$W$
be the convex hull of
![]() $X$
in
$X$
in
![]() $\textrm {cl}\Omega$
. Then
$\textrm {cl}\Omega$
. Then
![]() $U=W\cap \Omega$
contains the axis of each hyperbolic in
$U=W\cap \Omega$
contains the axis of each hyperbolic in
![]() $\Gamma$
, so
$\Gamma$
, so
![]() $U$
is non-empty, convex,
$U$
is non-empty, convex,
![]() $\Gamma$
-invariant. Since
$\Gamma$
-invariant. Since
![]() $U\subset \Omega$
, we have
$U\subset \Omega$
, we have
![]() $\Omega =U$
by (1.14). Since
$\Omega =U$
by (1.14). Since
![]() $\Omega$
is strictly convex it follows
$\Omega$
is strictly convex it follows
![]() $\textrm {Fr}\Omega =\textrm {cl} X$
.
$\textrm {Fr}\Omega =\textrm {cl} X$
.
Since
![]() $\Omega ^{\prime}$
is preserved by
$\Omega ^{\prime}$
is preserved by
![]() $\Gamma$
it follows that
$\Gamma$
it follows that
![]() $\textrm {cl}\Omega ^{\prime}\supset \textrm {cl} X$
. Now
$\textrm {cl}\Omega ^{\prime}\supset \textrm {cl} X$
. Now
![]() $\textrm {Fr}\Omega$
is a convex hypersurface of dimension
$\textrm {Fr}\Omega$
is a convex hypersurface of dimension
![]() $n-1\gt 0$
. Only one side of
$n-1\gt 0$
. Only one side of
![]() $\textrm {Fr}\Omega$
is locally convex. Hence
$\textrm {Fr}\Omega$
is locally convex. Hence
![]() $\Omega ^{\prime}$
contains points on the same side of
$\Omega ^{\prime}$
contains points on the same side of
![]() $\textrm {Fr}\Omega$
as
$\textrm {Fr}\Omega$
as
![]() $\Omega$
. Thus
$\Omega$
. Thus
![]() $U^{\prime}=\Omega ^{\prime}\cap \Omega \ne \emptyset$
is properly convex and is preserved by
$U^{\prime}=\Omega ^{\prime}\cap \Omega \ne \emptyset$
is properly convex and is preserved by
![]() $\Gamma$
. By (1.14)
$\Gamma$
. By (1.14)
![]() $\Omega =U^{\prime}=\Omega ^{\prime}$
.
$\Omega =U^{\prime}=\Omega ^{\prime}$
.
2. Convex cones
This section is based on work of Vinberg, as simplified by Goldman. Write
![]() $V={\mathbb{R}}^{n+1}$
. If
$V={\mathbb{R}}^{n+1}$
. If
![]() $\Omega$
is properly convex there is a nice convex hypersurface in the cone
$\Omega$
is properly convex there is a nice convex hypersurface in the cone
![]() $\mathcal{C}\Omega$
that is preserved by every projective automorphism of
$\mathcal{C}\Omega$
that is preserved by every projective automorphism of
![]() $\mathcal{C}\Omega$
. This is a generalization of the hyperboloid model of hyperbolic space that sits inside the lightcone. In general there is a choice of such surfaces. One is Vinberg’s characteristic surface, and another is an affine sphere. The characteristic surface is defined below using a simple geometric condition. One consequence of this is (2.8), which provides an analogue of the centroid for properly convex subsets of the sphere. The purpose of this section is to prove the following and derive some consequences.
$\mathcal{C}\Omega$
. This is a generalization of the hyperboloid model of hyperbolic space that sits inside the lightcone. In general there is a choice of such surfaces. One is Vinberg’s characteristic surface, and another is an affine sphere. The characteristic surface is defined below using a simple geometric condition. One consequence of this is (2.8), which provides an analogue of the centroid for properly convex subsets of the sphere. The purpose of this section is to prove the following and derive some consequences.
Theorem 2.1.
Suppose
![]() $\mathcal{C}$
is a properly convex cone in
$\mathcal{C}$
is a properly convex cone in
![]() $V$
. Let
$V$
. Let
![]() $\mathcal{D}$
be the intersection of all closed affine half-spaces
$\mathcal{D}$
be the intersection of all closed affine half-spaces
![]() $H\subset V$
such that
$H\subset V$
such that
![]() $\textrm {vol}(\mathcal{C}\setminus H)=1$
. Then we have the following:
$\textrm {vol}(\mathcal{C}\setminus H)=1$
. Then we have the following:
-
(i)
 $\mathcal{D}\subset \mathcal{C}$
;
$\mathcal{D}\subset \mathcal{C}$
; -
(ii)
 $\partial \mathcal{D}$
is a strictly convex hypersurface;
$\partial \mathcal{D}$
is a strictly convex hypersurface;
-
(iii)
 $\partial \mathcal{D}$
meets every ray in
$\partial \mathcal{D}$
meets every ray in
 $\mathcal{C}$
once;
$\mathcal{C}$
once;
-
(iv)
 $\partial \mathcal{D}$
is preserved by
$\partial \mathcal{D}$
is preserved by
 $\textrm {SL}_{\pm }(\mathcal{C})$
;
$\textrm {SL}_{\pm }(\mathcal{C})$
; -
(v) if
 $T$
is a supporting hyperplane to
$T$
is a supporting hyperplane to
 $\mathcal{D}$
, then
$\mathcal{D}$
, then
 $T\cap \mathcal{D}$
is the centroid of
$T\cap \mathcal{D}$
is the centroid of
 $T\cap \mathcal{C}$
(see Figure
4
);
$T\cap \mathcal{C}$
(see Figure
4
);
-
(vi)
 $\partial \mathcal{D}$
is
$\partial \mathcal{D}$
is
 $C^1$
.
$C^1$
.
In the special case that
![]() $\mathcal{C}$
is the cone on a round ball, then
$\mathcal{C}$
is the cone on a round ball, then
![]() $\partial \mathcal{D}$
is the hyperboloid model of hyperbolic space. Fix an inner product
$\partial \mathcal{D}$
is the hyperboloid model of hyperbolic space. Fix an inner product
![]() $\langle \;\cdot \;,\;\cdot \;\rangle$
on
$\langle \;\cdot \;,\;\cdot \;\rangle$
on
![]() $V$
. This determines a norm on
$V$
. This determines a norm on
![]() $V$
, and induces a Riemannian metric and associated volume form on every smooth submanifold of
$V$
, and induces a Riemannian metric and associated volume form on every smooth submanifold of
![]() $V$
.
$V$
.
The centroid of a bounded convex set
![]() $K$
in
$K$
in
![]() $V$
is the point
$V$
is the point
![]() $\mu (K)$
in
$\mu (K)$
in
![]() $K$
given by
$K$
given by
Here,
![]() $\dim K\leqslant \dim V$
and
$\dim K\leqslant \dim V$
and
![]() $\textrm {dvol}_K$
is the induced volume form on
$\textrm {dvol}_K$
is the induced volume form on
![]() $K$
. The centroid is independent of the inner product.
$K$
. The centroid is independent of the inner product.

Figure 4. Here,
![]() $T\cap \mathcal{D}$
is the centroid of
$T\cap \mathcal{D}$
is the centroid of
![]() $T\cap \mathcal{C}$
.
$T\cap \mathcal{C}$
.
Let
![]() $S^n=\{x\in V:\ \|x\|^2=1\}$
. Suppose
$S^n=\{x\in V:\ \|x\|^2=1\}$
. Suppose
![]() $\Omega$
is an open, properly convex subset of
$\Omega$
is an open, properly convex subset of
![]() $S^n$
and
$S^n$
and
![]() $\mathcal{C}=\mathcal{C}\Omega$
is the corresponding cone in
$\mathcal{C}=\mathcal{C}\Omega$
is the corresponding cone in
![]() $V$
. Given
$V$
. Given
![]() $0\ne \phi \in V^*$
, the set
$0\ne \phi \in V^*$
, the set
![]() $\phi ^{-1}(1)$
is an affine hyperplane in
$\phi ^{-1}(1)$
is an affine hyperplane in
![]() $V$
. If
$V$
. If
![]() $\phi \in \mathcal{C}^*$
, then
$\phi \in \mathcal{C}^*$
, then
![]() $\phi (\mathcal{C})\gt 0$
, so
$\phi (\mathcal{C})\gt 0$
, so
![]() $\mathcal{C}_{\phi }=\{x\in \mathcal{C}: \phi (x)=1\}$
is a bounded subset of this hyperplane that separates
$\mathcal{C}_{\phi }=\{x\in \mathcal{C}: \phi (x)=1\}$
is a bounded subset of this hyperplane that separates
![]() $\mathcal{C}$
. The subset of
$\mathcal{C}$
. The subset of
![]() $\mathcal{C}$
below this hyperplane is
$\mathcal{C}$
below this hyperplane is
![]() $\mathcal{C}\cap \phi ^{-1}(0,1]$
, and has finite volume and boundary
$\mathcal{C}\cap \phi ^{-1}(0,1]$
, and has finite volume and boundary
![]() $\mathcal{C}_{\phi }$
. The centroid of
$\mathcal{C}_{\phi }$
. The centroid of
![]() $\mathcal{C}_{\phi }$
is a point
$\mathcal{C}_{\phi }$
is a point
![]() $\mu (\mathcal{C}_{\phi })\in \mathcal{C}$
. Define
$\mu (\mathcal{C}_{\phi })\in \mathcal{C}$
. Define
![]() $\Theta (\phi )=\mu (\mathcal{C}_{\phi })$
. We will show this is a homeomorphism
$\Theta (\phi )=\mu (\mathcal{C}_{\phi })$
. We will show this is a homeomorphism
![]() $\Theta :\mathcal{C}^*\rightarrow \mathcal{C}$
.
$\Theta :\mathcal{C}^*\rightarrow \mathcal{C}$
.
The volume function
![]() $\mathcal{V}:\mathcal{C}^*\to {\mathbb{R}}$
is defined by
$\mathcal{V}:\mathcal{C}^*\to {\mathbb{R}}$
is defined by
Let
![]() $\pi :\mathcal{C}_{\phi }\to \Omega =S^n\cap \mathcal{C}$
be the radial projection
$\pi :\mathcal{C}_{\phi }\to \Omega =S^n\cap \mathcal{C}$
be the radial projection
![]() $\pi (x)=x/\|x\|$
. Let
$\pi (x)=x/\|x\|$
. Let
![]() $\textrm {dB}$
be the induced volume form on
$\textrm {dB}$
be the induced volume form on
![]() $S^n$
. We compute this integral in polar coordinates, so
$S^n$
. We compute this integral in polar coordinates, so
![]() $\textrm {dvol}=r^{n} \textrm {dr}\wedge \pi ^*\textrm {dB}$
.
$\textrm {dvol}=r^{n} \textrm {dr}\wedge \pi ^*\textrm {dB}$
.
Given
![]() $\phi \in \mathcal{C}^*$
, there is
$\phi \in \mathcal{C}^*$
, there is
![]() $v\in V$
such that
$v\in V$
such that
![]() $\phi (x)=\langle x,v\rangle$
for all
$\phi (x)=\langle x,v\rangle$
for all
![]() $x\in V$
. Let
$x\in V$
. Let
![]() $y=\pi (x)$
. If
$y=\pi (x)$
. If
![]() $\phi (x)=1$
, then
$\phi (x)=1$
, then
Using polar coordinates
 \begin{align} \mathcal{V}(\phi )=\int _{C_{\phi }\cap \phi ^{-1}(0,1]}r^n\textrm {dr}\wedge \pi ^*\textrm {dB}= \int _{\Omega }\left (\int _0^{\langle y,v\rangle ^{-1}} r^n \textrm {dr}\right )\textrm {dB}_y =(n+1)^{-1}\int _{\Omega }\langle y,v\rangle ^{-n-1}\; \textrm {dB}_y. \end{align}
\begin{align} \mathcal{V}(\phi )=\int _{C_{\phi }\cap \phi ^{-1}(0,1]}r^n\textrm {dr}\wedge \pi ^*\textrm {dB}= \int _{\Omega }\left (\int _0^{\langle y,v\rangle ^{-1}} r^n \textrm {dr}\right )\textrm {dB}_y =(n+1)^{-1}\int _{\Omega }\langle y,v\rangle ^{-n-1}\; \textrm {dB}_y. \end{align}
For
![]() $q\in \mathcal{C}$
, the set
$q\in \mathcal{C}$
, the set
![]() $\mathcal{C}^*_q=\{\phi \in \mathcal{C}^*:\ \phi (q)=1\ \}$
is the intersection of a hyperplane in
$\mathcal{C}^*_q=\{\phi \in \mathcal{C}^*:\ \phi (q)=1\ \}$
is the intersection of a hyperplane in
![]() $V^*$
with
$V^*$
with
![]() $\mathcal{C}^*$
, and has compact closure. Elements of
$\mathcal{C}^*$
, and has compact closure. Elements of
![]() $\mathcal{C}^*_q$
correspond to hyperplanes in
$\mathcal{C}^*_q$
correspond to hyperplanes in
![]() $V_0$
that contain
$V_0$
that contain
![]() $q$
and separate
$q$
and separate
![]() $\mathcal{C}$
.
$\mathcal{C}$
.
Proposition 2.2. The volume function has the following properties:
-
(i)
 $\mathcal{V}$
is smooth and strictly convex;
$\mathcal{V}$
is smooth and strictly convex;
-
(ii)
 $\mathcal{V}(\phi )\to \infty$
as
$\mathcal{V}(\phi )\to \infty$
as
 $\phi \to \textrm {Fr}\mathcal{C}^*$
;
$\phi \to \textrm {Fr}\mathcal{C}^*$
; -
(iii)
 $\mathcal{V}(t\cdot \phi )=t^{-n-1}\mathcal{V}(\phi )$
for all
$\mathcal{V}(t\cdot \phi )=t^{-n-1}\mathcal{V}(\phi )$
for all
 $t\gt 0$
;
$t\gt 0$
; -
(iv) there is a unique
 $\phi \in \mathcal{C}^*_q$
at which
$\phi \in \mathcal{C}^*_q$
at which
 $\mathcal{V}|\mathcal{C}^*_q$
attains a minimum and
$\mathcal{V}|\mathcal{C}^*_q$
attains a minimum and
 $q=\mu (\mathcal{C}_{\phi })$
.
$q=\mu (\mathcal{C}_{\phi })$
.
Proof.
We use the inner product to identify
![]() $V$
with
$V$
with
![]() $V^*$
so that
$V^*$
so that
![]() $\mathcal{C}^*$
is a subset of
$\mathcal{C}^*$
is a subset of
![]() $V$
and
$V$
and
We also regard
![]() $\mathcal{V}(\phi )$
as the function
$\mathcal{V}(\phi )$
as the function
![]() $\mathcal{W}(v)$
given by the right-hand side of (3) and prove corresponding statements for
$\mathcal{W}(v)$
given by the right-hand side of (3) and prove corresponding statements for
![]() $\mathcal{W}$
.
$\mathcal{W}$
.
For fixed
![]() $y$
, the integrand
$y$
, the integrand
![]() $f(v)=\langle y,v\rangle ^{-n-1}$
in (3) is a smooth and convex function of
$f(v)=\langle y,v\rangle ^{-n-1}$
in (3) is a smooth and convex function of
![]() $v$
. It follows that
$v$
. It follows that
![]() $\mathcal{W}(v)$
is a smooth, strictly convex function of
$\mathcal{W}(v)$
is a smooth, strictly convex function of
![]() $v$
. This proves (i).
$v$
. This proves (i).
If
![]() $0\ne \psi \in \textrm {Fr}\mathcal{C}^*$
, then there is
$0\ne \psi \in \textrm {Fr}\mathcal{C}^*$
, then there is
![]() $0\ne x\in \textrm {Fr}\mathcal{C}$
with
$0\ne x\in \textrm {Fr}\mathcal{C}$
with
![]() $\psi (x)=0$
. Thus
$\psi (x)=0$
. Thus
![]() ${\mathbb{R}}^+\cdot x\subset \textrm {cl}\mathcal{C}_{\psi }$
, so
${\mathbb{R}}^+\cdot x\subset \textrm {cl}\mathcal{C}_{\psi }$
, so
![]() $\mathcal{C}_{\psi }$
is not compact. Moreover
$\mathcal{C}_{\psi }$
is not compact. Moreover
![]() $\mathcal{C}_{\psi }$
is convex and has non-empty interior, so
$\mathcal{C}_{\psi }$
is convex and has non-empty interior, so
![]() $\textrm {vol}(\mathcal{C}_{\psi })=\infty$
. It easily follows that
$\textrm {vol}(\mathcal{C}_{\psi })=\infty$
. It easily follows that
![]() $\mathcal{V}(\phi )\to \infty$
as
$\mathcal{V}(\phi )\to \infty$
as
![]() $\phi \to \psi$
. This proves (ii), and (iii) follows from (3). It follows from convexity and (ii) that
$\phi \to \psi$
. This proves (ii), and (iii) follows from (3). It follows from convexity and (ii) that
![]() $\mathcal{V}|\mathcal{C}^*_q$
has a unique critical point, and it is a minimum.
$\mathcal{V}|\mathcal{C}^*_q$
has a unique critical point, and it is a minimum.
The gradient of
![]() $\mathcal{W}(v)$
is
$\mathcal{W}(v)$
is
From the definition of
![]() $\mathcal{C}^*_q$
it follows that the condition for a critical point is that
$\mathcal{C}^*_q$
it follows that the condition for a critical point is that
![]() $\nabla \mathcal{W}\in {\mathbb{R}}\cdot q$
. We use radial projection
$\nabla \mathcal{W}\in {\mathbb{R}}\cdot q$
. We use radial projection
![]() $\pi$
to change variables in (4) to obtain (6).
$\pi$
to change variables in (4) to obtain (6).
Refer to Figure 5. Let
![]() $v\in V$
be dual to
$v\in V$
be dual to
![]() $\phi$
, so
$\phi$
, so
![]() $\phi (x)=\langle x,v\rangle$
. Thus
$\phi (x)=\langle x,v\rangle$
. Thus
![]() $\phi (v\|v\|^{-2})=1$
and
$\phi (v\|v\|^{-2})=1$
and
![]() $v\|v\|^{-2}$
is the point on
$v\|v\|^{-2}$
is the point on
![]() $\phi ^{-1}(1)$
closest to
$\phi ^{-1}(1)$
closest to
![]() $0$
. Thus the distance of
$0$
. Thus the distance of
![]() $\phi ^{-1}(1)$
from
$\phi ^{-1}(1)$
from
![]() $0$
is
$0$
is
![]() $\|v\|^{-1}$
. Given
$\|v\|^{-1}$
. Given
![]() $x\in \mathcal{C}_{\phi }$
, then
$x\in \mathcal{C}_{\phi }$
, then
![]() $1=\phi (x)=\langle x,v\rangle$
. Set
$1=\phi (x)=\langle x,v\rangle$
. Set
![]() $y=\pi (x)$
, then
$y=\pi (x)$
, then
![]() $\|y\|=1$
, and define
$\|y\|=1$
, and define
![]() $\cos \theta =\langle y,v\rangle /\|v\|$
. Since
$\cos \theta =\langle y,v\rangle /\|v\|$
. Since
![]() $\langle x,v\rangle=1$
it follows that
$\langle x,v\rangle=1$
it follows that
![]() $x=y/\langle y,v\rangle$
and so
$x=y/\langle y,v\rangle$
and so
![]() $\|x\|=1/\langle y,v\rangle$
.
$\|x\|=1/\langle y,v\rangle$
.
Let
![]() $S_x\subset {\mathbb{R}}^{n+1}$
denote the sphere with center
$S_x\subset {\mathbb{R}}^{n+1}$
denote the sphere with center
![]() $0$
and radius
$0$
and radius
![]() $\|x\|$
. The volume form on
$\|x\|$
. The volume form on
![]() $S_x$
is
$S_x$
is
![]() $d_{S_x}=\|x\|^{n}\pi _1^*dB_y$
, where
$d_{S_x}=\|x\|^{n}\pi _1^*dB_y$
, where
![]() $\pi _1:S_x\rightarrow S^n$
is radial projection. Let
$\pi _1:S_x\rightarrow S^n$
is radial projection. Let
![]() $d A_x$
be the volume element on
$d A_x$
be the volume element on
![]() $\mathcal{C}_{\phi }$
. Then
$\mathcal{C}_{\phi }$
. Then
![]() $dA_x=(\cos \theta )^{-1}\pi _2^*d_{S_x}$
, where
$dA_x=(\cos \theta )^{-1}\pi _2^*d_{S_x}$
, where
![]() $\pi _2:\mathcal{C}_{\phi }\rightarrow S_x$
is radial projection. Then
$\pi _2:\mathcal{C}_{\phi }\rightarrow S_x$
is radial projection. Then
![]() $\pi =\pi _1\circ \pi _2:\mathcal{C}_{\phi }\rightarrow S^n$
is radial projection, and combining gives
$\pi =\pi _1\circ \pi _2:\mathcal{C}_{\phi }\rightarrow S^n$
is radial projection, and combining gives
It follows from (4) and (5) that
Since the condition for a critical point is
![]() $\nabla \mathcal{W}\in {\mathbb{R}}\cdot q$
, this happens when
$\nabla \mathcal{W}\in {\mathbb{R}}\cdot q$
, this happens when
The centroid
![]() $\mu (\mathcal{C}_{\phi })$
is in
$\mu (\mathcal{C}_{\phi })$
is in
![]() $\mathcal{C}_{\phi }$
, and
$\mathcal{C}_{\phi }$
, and
![]() $q\in \mathcal{C}_{\phi }$
. Hence at the minimum we have
$q\in \mathcal{C}_{\phi }$
. Hence at the minimum we have
![]() $\mu (\mathcal{C}_{\phi })=q$
, proving (iv).
$\mu (\mathcal{C}_{\phi })=q$
, proving (iv).

Figure 5. Volume forms on
![]() $\Omega \subset S^n$
and
$\Omega \subset S^n$
and
![]() $\mathcal{C}_{\phi }$
.
$\mathcal{C}_{\phi }$
.
Proof of Theorem 2.1. Clearly
![]() $\mathcal{D}$
is a closed convex subset of
$\mathcal{D}$
is a closed convex subset of
![]() $V$
. Given
$V$
. Given
![]() $q\in \mathcal{C}$
, there is
$q\in \mathcal{C}$
, there is
![]() $\phi \in \mathcal{C}^*$
given by (2.2)(iv). Then by (2.2)(iii) there is
$\phi \in \mathcal{C}^*$
given by (2.2)(iv). Then by (2.2)(iii) there is
![]() $t\gt 0$
such that
$t\gt 0$
such that
![]() $\mathcal{V}(t\cdot \phi )=1$
. Replace
$\mathcal{V}(t\cdot \phi )=1$
. Replace
![]() $\phi$
by
$\phi$
by
![]() $t\cdot \phi$
and replace
$t\cdot \phi$
and replace
![]() $q$
by
$q$
by
![]() $t^{-1}q$
. Then
$t^{-1}q$
. Then
![]() $\mathcal{V}(\phi )=1$
and the hyperplane
$\mathcal{V}(\phi )=1$
and the hyperplane
![]() $T_{\phi }=\phi ^{-1}(1)$
contains
$T_{\phi }=\phi ^{-1}(1)$
contains
![]() $q$
. The half-space
$q$
. The half-space
![]() $H={\phi }^{-1}[1,\infty )$
has the property that
$H={\phi }^{-1}[1,\infty )$
has the property that
![]() $\textrm {vol}(\mathcal{C}\setminus H)=1$
, so
$\textrm {vol}(\mathcal{C}\setminus H)=1$
, so
![]() $\mathcal{D}\subset H$
.
$\mathcal{D}\subset H$
.
Suppose that
![]() $\mathcal{V}(\psi )=1$
and
$\mathcal{V}(\psi )=1$
and
![]() $\psi \ne \phi$
, then
$\psi \ne \phi$
, then
![]() $\lambda =\psi (q)\gt 1$
since otherwise if
$\lambda =\psi (q)\gt 1$
since otherwise if
![]() $\psi ^{\prime}=\lambda ^{-1}\psi \in \mathcal{C}^*_q$
and
$\psi ^{\prime}=\lambda ^{-1}\psi \in \mathcal{C}^*_q$
and
![]() $\mathcal{V}(\psi ^{\prime})=\lambda ^{n+1}\leqslant 1$
. This contradicts that
$\mathcal{V}(\psi ^{\prime})=\lambda ^{n+1}\leqslant 1$
. This contradicts that
![]() $\phi$
is the unique minimum of
$\phi$
is the unique minimum of
![]() $\mathcal{V}|\mathcal{C}^*$
. Hence
$\mathcal{V}|\mathcal{C}^*$
. Hence
![]() ${\psi }(q)\gt 1$
so
${\psi }(q)\gt 1$
so
![]() $q\in \partial \mathcal{D}$
and
$q\in \partial \mathcal{D}$
and
![]() $T_{\phi }$
is a supporting hyperplane to
$T_{\phi }$
is a supporting hyperplane to
![]() $\mathcal{D}$
at
$\mathcal{D}$
at
![]() $q$
. Also
$q$
. Also
![]() $q=T_{\phi }\cap \mathcal{D}$
is the centroid of
$q=T_{\phi }\cap \mathcal{D}$
is the centroid of
![]() $\mathcal{C}_{\phi }$
by (iv). This proves (2) and (5). It also follows that
$\mathcal{C}_{\phi }$
by (iv). This proves (2) and (5). It also follows that
![]() $\mathcal{D}\cap ({\mathbb{R}}^+\cdot q)=[1,\infty )\cdot q$
, which proves (3).
$\mathcal{D}\cap ({\mathbb{R}}^+\cdot q)=[1,\infty )\cdot q$
, which proves (3).

Figure 6. Approaching the frontier.
Suppose that
![]() $T$
is any supporting hyperplane at
$T$
is any supporting hyperplane at
![]() $q$
. Then there is
$q$
. Then there is
![]() $\psi \in V^*$
with
$\psi \in V^*$
with
![]() $T=\psi ^{-1}(1)$
and
$T=\psi ^{-1}(1)$
and
![]() $\psi (\mathcal{D})\geqslant 1$
. The same reasoning shows that
$\psi (\mathcal{D})\geqslant 1$
. The same reasoning shows that
![]() $\phi =\psi$
, thus
$\phi =\psi$
, thus
![]() $T_{\phi }$
is the unique supporting hyperplane at
$T_{\phi }$
is the unique supporting hyperplane at
![]() $q$
, which proves (6). Now (4) follows from the fact that
$q$
, which proves (6). Now (4) follows from the fact that
![]() $\textrm {SL}(\mathcal{C})$
preserves volume.
$\textrm {SL}(\mathcal{C})$
preserves volume.
It only remains to prove (1). Refer to Figure 6. Since
![]() $\mathcal{D}$
is convex, it suffices to prove
$\mathcal{D}$
is convex, it suffices to prove
![]() $\mathcal{D}$
contains no point in the frontier of
$\mathcal{D}$
contains no point in the frontier of
![]() $\mathcal{C}$
. Suppose
$\mathcal{C}$
. Suppose
![]() $x\in \mathcal{D}\cap \textrm {Fr}\mathcal{C}$
. Then
$x\in \mathcal{D}\cap \textrm {Fr}\mathcal{C}$
. Then
![]() $x\ne 0$
by definition of
$x\ne 0$
by definition of
![]() $\mathcal{D}$
. Choose
$\mathcal{D}$
. Choose
![]() $y\in \mathcal{C}$
and let
$y\in \mathcal{C}$
and let
![]() $U\subset V$
be the two-dimensional vector subspace that contains both
$U\subset V$
be the two-dimensional vector subspace that contains both
![]() $x$
and
$x$
and
![]() $y$
. Let
$y$
. Let
![]() $x_n$
be a sequence in
$x_n$
be a sequence in
![]() $(x,y)$
that converges to
$(x,y)$
that converges to
![]() $x$
. When
$x$
. When
![]() $x_n$
is close to
$x_n$
is close to
![]() $x$
, there is a half-space
$x$
, there is a half-space
![]() $H^{\prime}_n$
with
$H^{\prime}_n$
with
![]() $x_n\in \partial H^{\prime}_n$
and
$x_n\in \partial H^{\prime}_n$
and
![]() $\textrm {vol}(\mathcal{C}\setminus H^{\prime}_n)$
is very small. Thus if
$\textrm {vol}(\mathcal{C}\setminus H^{\prime}_n)$
is very small. Thus if
![]() $\phi _n\in \mathcal{C}^*_{x_n}$
is as given by (iv), then
$\phi _n\in \mathcal{C}^*_{x_n}$
is as given by (iv), then
![]() $\epsilon _n=\mathcal{V}(\phi _n)\to 0$
as
$\epsilon _n=\mathcal{V}(\phi _n)\to 0$
as
![]() $n\to \infty$
. Since
$n\to \infty$
. Since
![]() $x$
is above
$x$
is above
![]() $\partial H_n=\phi _n^{-1}(1)$
it follows that
$\partial H_n=\phi _n^{-1}(1)$
it follows that
![]() $y$
is below
$y$
is below
![]() $y_n=({\mathbb{R}}\cdot y)\cap \partial H_n$
.
$y_n=({\mathbb{R}}\cdot y)\cap \partial H_n$
.
Let
![]() $\psi _n=\epsilon _n^{1/(n+1)}\phi _n$
, then by (2.2)(iii), we have
$\psi _n=\epsilon _n^{1/(n+1)}\phi _n$
, then by (2.2)(iii), we have
![]() $\mathcal{V}(\psi _n)=1$
. Then
$\mathcal{V}(\psi _n)=1$
. Then
![]() $\mathcal{D}\subset \psi _n^{-1}[1,\infty )$
. The hyperplane
$\mathcal{D}\subset \psi _n^{-1}[1,\infty )$
. The hyperplane
![]() $T_n=\psi _n^{-1}(1)$
intersects
$T_n=\psi _n^{-1}(1)$
intersects
![]() ${\mathbb{R}}\cdot y$
at
${\mathbb{R}}\cdot y$
at
![]() $z_n=\epsilon _n^{-1/(n+1)}y_n$
. Since
$z_n=\epsilon _n^{-1/(n+1)}y_n$
. Since
![]() $\|y_n\|\gt \|y\|$
it follows that
$\|y_n\|\gt \|y\|$
it follows that
![]() $z_n\to \infty$
as
$z_n\to \infty$
as
![]() $n\to \infty$
. Let
$n\to \infty$
. Let
![]() $r_n$
be the distance of
$r_n$
be the distance of
![]() $z_n$
from
$z_n$
from
![]() $\partial \mathcal{C}$
. Then
$\partial \mathcal{C}$
. Then
![]() $r_n\to \infty$
. Half the ball of radius
$r_n\to \infty$
. Half the ball of radius
![]() $r_n$
center at
$r_n$
center at
![]() $z_n$
is below
$z_n$
is below
![]() $T_n$
and in
$T_n$
and in
![]() $\mathcal{C}$
. But this volume is at most
$\mathcal{C}$
. But this volume is at most
![]() $1$
. This contradicts the existence of
$1$
. This contradicts the existence of
![]() $x$
, proving (1).
$x$
, proving (1).
Corollary 2.3.
If
![]() $\Omega$
is properly convex, then
$\Omega$
is properly convex, then
![]() $\Theta :\mathcal{C}\Omega ^*\rightarrow \mathcal{C}\Omega$
is a homeomorphism that maps rays to rays, and
$\Theta :\mathcal{C}\Omega ^*\rightarrow \mathcal{C}\Omega$
is a homeomorphism that maps rays to rays, and
![]() $[\Theta ]:\Omega ^*\rightarrow \Omega$
is a homeomorphism.
$[\Theta ]:\Omega ^*\rightarrow \Omega$
is a homeomorphism.
Proof.
Given
![]() $p\in \Omega$
there is a unique
$p\in \Omega$
there is a unique
![]() $x\in \partial \mathcal{D}$
with
$x\in \partial \mathcal{D}$
with
![]() $p=[x]$
. By (2.2)(iv) there is a unique
$p=[x]$
. By (2.2)(iv) there is a unique
![]() $\phi \in \mathcal{C}^*$
with
$\phi \in \mathcal{C}^*$
with
![]() $\phi (x)=1$
and
$\phi (x)=1$
and
![]() $\mathcal{V}(\phi )=1$
. Moreover
$\mathcal{V}(\phi )=1$
. Moreover
![]() $\mu (\mathcal{C}_{\phi })=x$
and so
$\mu (\mathcal{C}_{\phi })=x$
and so
![]() $[\Theta ][\phi ]=p$
. Hence
$[\Theta ][\phi ]=p$
. Hence
![]() $[\Theta ]$
is a bijection. Clearly
$[\Theta ]$
is a bijection. Clearly
![]() $\Theta$
is continuous. By (2.2)(ii)
$\Theta$
is continuous. By (2.2)(ii)
![]() $[\Theta ]$
is proper, and thus a homeomorphism. Since
$[\Theta ]$
is proper, and thus a homeomorphism. Since
![]() $\Theta (t x)=t^{-n-1}\Theta (x)$
, rays are mapped to rays. It follows that
$\Theta (t x)=t^{-n-1}\Theta (x)$
, rays are mapped to rays. It follows that
![]() $\Theta$
is also a homeomorphism.
$\Theta$
is also a homeomorphism.
The dual action of
![]() $A\in \textrm {SL} _{\pm }V$
on
$A\in \textrm {SL} _{\pm }V$
on
![]() ${\mathbb{P}} V^*$
is given by
${\mathbb{P}} V^*$
is given by
![]() $A[\phi ]=[\phi \circ A^{-1}]$
. If
$A[\phi ]=[\phi \circ A^{-1}]$
. If
![]() $\Gamma \subset \textrm {SL}_{\pm } V$
and preserves
$\Gamma \subset \textrm {SL}_{\pm } V$
and preserves
![]() $\Omega$
, then the dual action of
$\Omega$
, then the dual action of
![]() $\Gamma$
preserves
$\Gamma$
preserves
![]() $\Omega ^*$
. It is clear that
$\Omega ^*$
. It is clear that
![]() $\Theta$
is equivariant with respect to these actions. The following directly follows from (1.5) and (2.3).
$\Theta$
is equivariant with respect to these actions. The following directly follows from (1.5) and (2.3).
Corollary 2.4 (Vinberg). If
![]() $M=\Omega /\Gamma$
is a closed, properly convex manifold, then
$M=\Omega /\Gamma$
is a closed, properly convex manifold, then
![]() $M^*=\Omega ^*/\Gamma$
is a properly convex manifold that is homeomorphic to
$M^*=\Omega ^*/\Gamma$
is a properly convex manifold that is homeomorphic to
![]() $M$
. Thus
$M$
. Thus
![]() $\pi _1M\cong \pi _1M^*$
.
$\pi _1M\cong \pi _1M^*$
.
If
![]() $M=\Omega /\Gamma$
, then
$M=\Omega /\Gamma$
, then
![]() $M$
is called
$M$
is called
![]() $C^1$
if
$C^1$
if
![]() $\Omega$
is
$\Omega$
is
![]() $C^1$
. From (1.5) we have the following.
$C^1$
. From (1.5) we have the following.
Corollary 2.5. The parameter
![]() $M$
is strictly convex if and only if
$M$
is strictly convex if and only if
![]() $M^*$
is
$M^*$
is
![]() $C^1$
.
$C^1$
.
Corollary 2.6.
If
![]() $M=\Omega /\Gamma$
is a closed, strictly convex manifold, then
$M=\Omega /\Gamma$
is a closed, strictly convex manifold, then
![]() $M^*=\Omega ^*/\Gamma$
is a closed, strictly convex manifold. We have
$M^*=\Omega ^*/\Gamma$
is a closed, strictly convex manifold. We have
![]() $\pi _1M\cong \pi _1M^*$
and call
$\pi _1M\cong \pi _1M^*$
and call
![]() $M^*$
the dual of
$M^*$
the dual of
![]() $M$
. Moreover,
$M$
. Moreover,
![]() $M$
is
$M$
is
![]() $C^1$
.
$C^1$
.
Proof.
Since
![]() $M$
is strictly convex, it is properly convex, so
$M$
is strictly convex, it is properly convex, so
![]() $M^*$
is a properly convex manifold, and
$M^*$
is a properly convex manifold, and
![]() $\pi _1M\cong \pi _1M^*$
. By (1.10) and (1.11)
$\pi _1M\cong \pi _1M^*$
. By (1.10) and (1.11)
![]() $M^*$
is closed, and strictly convex. Thus
$M^*$
is closed, and strictly convex. Thus
![]() $M=(M^*)^*$
is
$M=(M^*)^*$
is
![]() $C^1$
by (1.5).
$C^1$
by (1.5).
The centroid of a bounded open convex set
![]() $\Omega \subset {\mathbb R}^n$
is a distinguished point in
$\Omega \subset {\mathbb R}^n$
is a distinguished point in
![]() $\Omega$
. We wish to define something similar for certain subsets of the sphere
$\Omega$
. We wish to define something similar for certain subsets of the sphere
![]() $S^n=\{x\in {\mathbb{R}}^{n+1}:\|x\|=1\}$
. Imagine a room that contains a transparent globe close to one wall, with a light source at the center of the globe. The shadow of Belgium appears on the wall. You can rotate the globe so that the centroid of this shadow is the point
$S^n=\{x\in {\mathbb{R}}^{n+1}:\|x\|=1\}$
. Imagine a room that contains a transparent globe close to one wall, with a light source at the center of the globe. The shadow of Belgium appears on the wall. You can rotate the globe so that the centroid of this shadow is the point
![]() $p$
on the wall closest to the center of the globe. The point on the globe that projects to
$p$
on the wall closest to the center of the globe. The point on the globe that projects to
![]() $p$
is called the (spherical) center of Belgium.
$p$
is called the (spherical) center of Belgium.
The open hemisphere that is the
![]() $\pi /2$
neighborhood of
$\pi /2$
neighborhood of
![]() $y\in S^n$
is
$y\in S^n$
is
![]() $U_y=\{x\in S^n: \langle x,y\rangle \gt 0\}$
. Radial projection
$U_y=\{x\in S^n: \langle x,y\rangle \gt 0\}$
. Radial projection
![]() $\pi _y:U_y\longrightarrow {\textrm {T}_y}S^n$
from the origin onto the tangent space to
$\pi _y:U_y\longrightarrow {\textrm {T}_y}S^n$
from the origin onto the tangent space to
![]() ${\mathbb{R}\textrm {P}_+}^n$
at
${\mathbb{R}\textrm {P}_+}^n$
at
![]() $y$
is given by
$y$
is given by
where we identify
![]() $S^n$
with
$S^n$
with
![]() ${\mathbb{R}\textrm {P}_+}^n$
.
${\mathbb{R}\textrm {P}_+}^n$
.
Definition 2.7.
If
![]() $\Omega \subset {\mathbb{R}\textrm {P}_+}^n$
is properly convex and
$\Omega \subset {\mathbb{R}\textrm {P}_+}^n$
is properly convex and
![]() $\Omega ^*=\{y\in S^n:\ \langle x,y\rangle \gt 0\ \textrm {\ for \ all \ } x\in \textrm {cl}(\Omega )\}$
, then
$\Omega ^*=\{y\in S^n:\ \langle x,y\rangle \gt 0\ \textrm {\ for \ all \ } x\in \textrm {cl}(\Omega )\}$
, then
![]() $y\in \Omega ^*$
is called a (spherical) center of
$y\in \Omega ^*$
is called a (spherical) center of
![]() $\Omega$
if
$\Omega$
if
![]() $\hat {\mu }(\pi _y(\Omega ))=\pi _y(y)$
.
$\hat {\mu }(\pi _y(\Omega ))=\pi _y(y)$
.
If
![]() $A\in {\textrm {O}}(n+1),$
then
$A\in {\textrm {O}}(n+1),$
then
![]() $A$
is an isometry of the inner product and so
$A$
is an isometry of the inner product and so
![]() $(A\Omega )^*=A(\Omega ^*)$
, and
$(A\Omega )^*=A(\Omega ^*)$
, and
![]() $Ay$
is a center of
$Ay$
is a center of
![]() $A\Omega$
if
$A\Omega$
if
![]() $y$
is a center of
$y$
is a center of
![]() $\Omega$
. The following property of
$\Omega$
. The following property of
![]() $\partial \mathcal{D}$
is important for the proof of the Closed Theorem.
$\partial \mathcal{D}$
is important for the proof of the Closed Theorem.
Theorem 2.8.
If
![]() $\Omega \subset S^n$
is properly convex, then it has a unique spherical center
$\Omega \subset S^n$
is properly convex, then it has a unique spherical center
![]() $[x]$
. Moreover
$[x]$
. Moreover
![]() $x$
is the point on
$x$
is the point on
![]() $\partial \mathcal{D}$
that minimizes
$\partial \mathcal{D}$
that minimizes
![]() $\|x\|$
.
$\|x\|$
.
Proof.
Let
![]() $\phi \in V^*$
be given by
$\phi \in V^*$
be given by
![]() $\phi (y)=\langle y,x\rangle$
. The tangent plane to
$\phi (y)=\langle y,x\rangle$
. The tangent plane to
![]() $\partial \mathcal{D}$
at
$\partial \mathcal{D}$
at
![]() $x$
is
$x$
is
![]() $\phi ^{-1}(1)$
and is orthogonal to
$\phi ^{-1}(1)$
and is orthogonal to
![]() $x$
. Thus
$x$
. Thus
![]() $\pi _x(\Omega )=\mathcal{C}_{\phi }$
and
$\pi _x(\Omega )=\mathcal{C}_{\phi }$
and
![]() $\mu (\mathcal{C}_{\phi })=x$
.
$\mu (\mathcal{C}_{\phi })=x$
.
Corollary 2.9.
If
![]() $\Omega \subset \mathbb{RP}^n$
is properly convex and
$\Omega \subset \mathbb{RP}^n$
is properly convex and
![]() $p\in \Omega$
, then there is an affine patch
$p\in \Omega$
, then there is an affine patch
![]() ${\mathbb{R}}^n\subset \mathbb{RP}^n$
such that
${\mathbb{R}}^n\subset \mathbb{RP}^n$
such that
![]() $p$
is the centroid of
$p$
is the centroid of
![]() $\Omega$
in
$\Omega$
in
![]() ${\mathbb{R}}^n$
.
${\mathbb{R}}^n$
.
Proof.
There is a unique
![]() $x\in \partial \mathcal{D}$
with
$x\in \partial \mathcal{D}$
with
![]() $p=[x]$
. Choose an inner product on
$p=[x]$
. Choose an inner product on
![]() $V$
so that
$V$
so that
![]() $x$
is the closest point to
$x$
is the closest point to
![]() $0$
on
$0$
on
![]() $\partial \mathcal{D}$
. The required affine patch is
$\partial \mathcal{D}$
. The required affine patch is
![]() $\mathbb{RP}^n\setminus {\mathbb{P}}(x^{\perp })$
.
$\mathbb{RP}^n\setminus {\mathbb{P}}(x^{\perp })$
.
3. Open
If
![]() $M$
is a closed
$M$
is a closed
![]() $(n-1)$
-manifold, then
$(n-1)$
-manifold, then
![]() $\pi _1M$
is finitely generated by some set of elements
$\pi _1M$
is finitely generated by some set of elements
![]() $g_1,\cdots ,g_k$
. Now,
$g_1,\cdots ,g_k$
. Now,
![]() $\rho \in \textrm {Rep}(M)$
is uniquely determined by the
$\rho \in \textrm {Rep}(M)$
is uniquely determined by the
![]() $k$
elements
$k$
elements
![]() $\rho (g_i)\in \textrm {PGL}(n,{\mathbb{R}})$
. The Veronese embedding embeds real-projective space (and thus
$\rho (g_i)\in \textrm {PGL}(n,{\mathbb{R}})$
. The Veronese embedding embeds real-projective space (and thus
![]() $\textrm {PGL}(n,{\mathbb{R}})$
) into a Euclidean space. This collection of elements can then be thought of as one point in a finite-dimensional real vector space
$\textrm {PGL}(n,{\mathbb{R}})$
) into a Euclidean space. This collection of elements can then be thought of as one point in a finite-dimensional real vector space
![]() $V$
. This gives an injective map of
$V$
. This gives an injective map of
![]() $\textrm {Rep}(M)$
into
$\textrm {Rep}(M)$
into
![]() $V$
. The Euclidean topology on
$V$
. The Euclidean topology on
![]() $\textrm {Rep}(M)$
is the subspace topology (of the standard topology on
$\textrm {Rep}(M)$
is the subspace topology (of the standard topology on
![]() $V$
) on the image of this map. In this topology
$V$
) on the image of this map. In this topology
![]() $\rho$
and
$\rho$
and
![]() $\rho ^{\prime}$
are close if there are matrix representatives of
$\rho ^{\prime}$
are close if there are matrix representatives of
![]() $\rho (g_i)$
and
$\rho (g_i)$
and
![]() $\rho ^{\prime}(g_i)$
that are close.
$\rho ^{\prime}(g_i)$
that are close.
Theorem 3.1 (Ehresmann–Thurston principle [Reference Bergeron and GelanderBG04]). Suppose that
![]() $M$
is a closed manifold of dimension
$M$
is a closed manifold of dimension
![]() $n$
. Then the subset of
$n$
. Then the subset of
![]() $\textrm {Rep}(M)$
consisting of the holonomies of real-projective structures on
$\textrm {Rep}(M)$
consisting of the holonomies of real-projective structures on
![]() $M$
is open in the Euclidean topology.
$M$
is open in the Euclidean topology.
Proof.
Let
![]() $\widetilde {M}$
be the universal cover of
$\widetilde {M}$
be the universal cover of
![]() $M$
. We identify
$M$
. We identify
![]() $\pi _1M$
with the group of covering transformations of
$\pi _1M$
with the group of covering transformations of
![]() $\widetilde M$
. Choose a triangulation
$\widetilde M$
. Choose a triangulation
![]() $\mathcal{T}_M$
of
$\mathcal{T}_M$
of
![]() $M$
. Let
$M$
. Let
![]() $\mathcal{T}$
be the lifted triangulation on
$\mathcal{T}$
be the lifted triangulation on
![]() $\widetilde M$
.
$\widetilde M$
.
Suppose that
![]() $\rho \in \textrm {Rep}(M)$
and there is a collection of maps
$\rho \in \textrm {Rep}(M)$
and there is a collection of maps
one for each simplex
![]() $\sigma$
in
$\sigma$
in
![]() $\mathcal{T}$
, satisfying the following properties.
$\mathcal{T}$
, satisfying the following properties.
-
(i) Equivariance. If
 $\sigma ^{\prime}=g\cdot \sigma$
for some
$\sigma ^{\prime}=g\cdot \sigma$
for some
 $g\in \pi _1M$
, then
$g\in \pi _1M$
, then \begin{equation*}f_{\sigma ^{\prime}}=\rho (g)\circ f_{\sigma }.\end{equation*}
\begin{equation*}f_{\sigma ^{\prime}}=\rho (g)\circ f_{\sigma }.\end{equation*}
-
(ii) Compatibility. If
 $\tau$
is a face of
$\tau$
is a face of
 $\sigma$
, then
$\sigma$
, then \begin{equation*}f_{\tau }=f_{\sigma }|\tau .\end{equation*}
\begin{equation*}f_{\tau }=f_{\sigma }|\tau .\end{equation*}
Compatibility implies there is a map
![]() $F:\widetilde {M}\longrightarrow \mathbb{RP}^n$
such that
$F:\widetilde {M}\longrightarrow \mathbb{RP}^n$
such that
![]() $F|\sigma =f_{\sigma }$
. Equivariance implies
$F|\sigma =f_{\sigma }$
. Equivariance implies
Suppose that
![]() $\textrm {dev}_0:\widetilde {M}\rightarrow \mathbb{RP}^n$
is the developing map, and
$\textrm {dev}_0:\widetilde {M}\rightarrow \mathbb{RP}^n$
is the developing map, and
![]() $\rho _0\in \textrm {Rep}(M)$
is the holonomy of some real-projective structure on
$\rho _0\in \textrm {Rep}(M)$
is the holonomy of some real-projective structure on
![]() $M$
. If
$M$
. If
![]() $\rho =\rho _0$
, then the collection
$\rho =\rho _0$
, then the collection
![]() $f_{\sigma }=\textrm {dev}_0|\sigma$
satisfies the required properties and
$f_{\sigma }=\textrm {dev}_0|\sigma$
satisfies the required properties and
![]() $F=\textrm {dev}_0$
.
$F=\textrm {dev}_0$
.
Choose the triangulation
![]() $\mathcal{T}_M$
of
$\mathcal{T}_M$
of
![]() $M$
to be by projective simplices. We show below that if
$M$
to be by projective simplices. We show below that if
![]() $\rho$
is close enough to
$\rho$
is close enough to
![]() $\rho _0$
, then the maps
$\rho _0$
, then the maps
![]() $f_{\sigma }$
may be chosen to be close to
$f_{\sigma }$
may be chosen to be close to
![]() $\textrm {dev}_0|\sigma$
on any finite set of simplices. If this finite collection contains a neighborhood,
$\textrm {dev}_0|\sigma$
on any finite set of simplices. If this finite collection contains a neighborhood,
![]() $U$
, of a fundamental domain
$U$
, of a fundamental domain
![]() $D$
, this will ensure
$D$
, this will ensure
![]() $F|U$
is a local homeomorphism. By equivariance
$F|U$
is a local homeomorphism. By equivariance
![]() $F$
is a local homeomorphism everywhere. Then
$F$
is a local homeomorphism everywhere. Then
![]() $F$
is a developing map for
$F$
is a developing map for
![]() $\rho$
, and this defines a projective structure on
$\rho$
, and this defines a projective structure on
![]() $M$
with holonomy
$M$
with holonomy
![]() $\rho$
,
$\rho$
,
It suffices to define
![]() $f_{\sigma }$
on one simplex in each
$f_{\sigma }$
on one simplex in each
![]() $\pi _1M$
orbit. Then the equivariance property defines the maps on the rest of the orbit. In order to ensure compatibility, we define the maps in order of increasing dimension of simplices. At each stage we have a well-defined equivariant map
$\pi _1M$
orbit. Then the equivariance property defines the maps on the rest of the orbit. In order to ensure compatibility, we define the maps in order of increasing dimension of simplices. At each stage we have a well-defined equivariant map
![]() $F_k:\mathcal{T}^k\rightarrow \mathbb{RP}^n$
defined on the
$F_k:\mathcal{T}^k\rightarrow \mathbb{RP}^n$
defined on the
![]() $k$
-skeleton
$k$
-skeleton
![]() $\mathcal{T}^k$
of
$\mathcal{T}^k$
of
![]() $\mathcal{T}$
. The extension process is to choose one
$\mathcal{T}$
. The extension process is to choose one
![]() $(k+1)$
-simplex
$(k+1)$
-simplex
![]() $\sigma$
in each
$\sigma$
in each
![]() $\pi _1M$
orbit, and define
$\pi _1M$
orbit, and define
![]() $f_{\sigma }$
to be a homeomorphism onto a projective simplex that has boundary
$f_{\sigma }$
to be a homeomorphism onto a projective simplex that has boundary
![]() $F_k(\partial \sigma )$
. By choosing
$F_k(\partial \sigma )$
. By choosing
![]() $\rho$
close enough to
$\rho$
close enough to
![]() $\rho _0$
we can arrange that the projective simplex
$\rho _0$
we can arrange that the projective simplex
![]() $f_{\sigma }(\sigma )$
is non-degenerate and close to
$f_{\sigma }(\sigma )$
is non-degenerate and close to
![]() $\textrm {dev}_0(\sigma )$
. The induction starts by choosing one vertex
$\textrm {dev}_0(\sigma )$
. The induction starts by choosing one vertex
![]() $v$
in each
$v$
in each
![]() $\pi _1M$
orbit and defining
$\pi _1M$
orbit and defining
![]() $f_v(v)=\textrm {dev}_0(v)$
.
$f_v(v)=\textrm {dev}_0(v)$
.
The next goal is to characterize properly convex manifolds in such a way that the above proof applies. A set is locally convex if every point has a convex neighborhood. There is a basic local-to-global principle for convexity.
Proposition 3.2.
If
![]() $K$
is a closed, connected, locally convex subset of
$K$
is a closed, connected, locally convex subset of
![]() ${\mathbb{R}}^n$
that is the closure of its interior, then
${\mathbb{R}}^n$
that is the closure of its interior, then
![]() $K$
is convex.
$K$
is convex.
Proof.
Suppose that
![]() $[x,y]$
is a segment in
$[x,y]$
is a segment in
![]() $K$
. Then
$K$
. Then
![]() $[x,y]\cap \partial K$
is closed. If
$[x,y]\cap \partial K$
is closed. If
![]() $(x,y)$
contains a point in
$(x,y)$
contains a point in
![]() $\partial K$
, then by local convexity
$\partial K$
, then by local convexity
![]() $[x,y]\cap \partial K$
is open in
$[x,y]\cap \partial K$
is open in
![]() $[x,y]$
. Thus
$[x,y]$
. Thus
![]() $[x,y]\subset \partial K$
. It follows that the union of the segments in
$[x,y]\subset \partial K$
. It follows that the union of the segments in
![]() $K$
with one endpoint
$K$
with one endpoint
![]() $x$
is open in
$x$
is open in
![]() $K$
. Since
$K$
. Since
![]() $K$
is closed, and the limit of segments is a segment, this subset is also closed. Since
$K$
is closed, and the limit of segments is a segment, this subset is also closed. Since
![]() $K$
is connected this set equals
$K$
is connected this set equals
![]() $K$
.
$K$
.
Local convexity only needs to be checked at points in
![]() $\partial K$
. Suppose that
$\partial K$
. Suppose that
![]() $K$
is contained in the upper half-space
$K$
is contained in the upper half-space
![]() $x_1\geqslant 0$
in
$x_1\geqslant 0$
in
![]() ${\mathbb{R}}^{n+1}$
. Then
${\mathbb{R}}^{n+1}$
. Then
![]() $K\cap (0\times {\mathbb{R}}^{n})$
is a convex subset of
$K\cap (0\times {\mathbb{R}}^{n})$
is a convex subset of
![]() ${\mathbb{R}}^n$
if the subset
${\mathbb{R}}^n$
if the subset
![]() $S\subset \partial K$
where
$S\subset \partial K$
where
![]() $x_1\gt 0$
is a locally convex hypersurface in
$x_1\gt 0$
is a locally convex hypersurface in
![]() ${\mathbb{R}}^{n+1}$
. Informally: a mountain with a convex surface has a convex base. We now extend this to show that a manifold is properly convex.
${\mathbb{R}}^{n+1}$
. Informally: a mountain with a convex surface has a convex base. We now extend this to show that a manifold is properly convex.
A projective manifold is convex if every pair of points is contained in a segment. If
![]() $M$
is a closed projective manifold, the argument in (3.2), that the union of the segments starting at a point is closed, fails. For example, consider the projective torus
$M$
is a closed projective manifold, the argument in (3.2), that the union of the segments starting at a point is closed, fails. For example, consider the projective torus
![]() $T$
that is the quotient of
$T$
that is the quotient of
![]() ${\mathbb{R}}^2_0$
by a cyclic group generated by a homothety. Then
${\mathbb{R}}^2_0$
by a cyclic group generated by a homothety. Then
![]() $T$
is not convex. Let
$T$
is not convex. Let
![]() $\pi :{\mathbb{R}}_0^2\rightarrow T$
be the projection. If
$\pi :{\mathbb{R}}_0^2\rightarrow T$
be the projection. If
![]() $x\in {\mathbb{R}}^2_0$
and
$x\in {\mathbb{R}}^2_0$
and
![]() $y_n\in {\mathbb{R}}^2_0$
is a sequence that converge to
$y_n\in {\mathbb{R}}^2_0$
is a sequence that converge to
![]() $-x$
then the Hausdorff limit of the segments
$-x$
then the Hausdorff limit of the segments
![]() $\pi [x,y_n]$
in
$\pi [x,y_n]$
in
![]() $T$
is not connected. It is the pair of rays,
$T$
is not connected. It is the pair of rays,
![]() $\pi [x,0)\cup \pi (0,-x]$
. Each ray maps into in one of the pair of circles
$\pi [x,0)\cup \pi (0,-x]$
. Each ray maps into in one of the pair of circles
![]() $\pi ({\mathbb{R}}_0\cdot x)\subset T$
.
$\pi ({\mathbb{R}}_0\cdot x)\subset T$
.
A smooth hypersurface
![]() $S\subset {\mathbb{R}}^n$
is Hessian convex if the surface is locally the zero-set of a smooth, real-valued function with positive–definite Hessian. Suppose
$S\subset {\mathbb{R}}^n$
is Hessian convex if the surface is locally the zero-set of a smooth, real-valued function with positive–definite Hessian. Suppose
![]() $\Omega \subset {\mathbb{RP}}^n_+$
is properly convex and
$\Omega \subset {\mathbb{RP}}^n_+$
is properly convex and
![]() $\mathcal{C}\Omega =\{v\in {\mathbb{R}}^{n+1}_0:[v]\in \Omega \}$
is the corresponding convex cone. Suppose
$\mathcal{C}\Omega =\{v\in {\mathbb{R}}^{n+1}_0:[v]\in \Omega \}$
is the corresponding convex cone. Suppose
![]() $M=\Omega /\Gamma$
is a compact, and properly convex,
$M=\Omega /\Gamma$
is a compact, and properly convex,
![]() $n$
-manifold. Then
$n$
-manifold. Then
![]() $\widetilde W=\mathcal{C}\Omega /\Gamma \cong M\times (0,\infty )$
is a properly convex affine
$\widetilde W=\mathcal{C}\Omega /\Gamma \cong M\times (0,\infty )$
is a properly convex affine
![]() $(n+1)$
-manifold. We may quotient out by a homothety to obtain a compact affine
$(n+1)$
-manifold. We may quotient out by a homothety to obtain a compact affine
![]() $(n+1)$
-manifold
$(n+1)$
-manifold
![]() $W\cong M\times S^1$
.
$W\cong M\times S^1$
.
By (2.1) there is a hypersurface
![]() $\partial \mathcal{D}\subset \mathcal{C}\Omega$
that is
$\partial \mathcal{D}\subset \mathcal{C}\Omega$
that is
![]() $\Gamma$
-invariant and Hessian convex away from
$\Gamma$
-invariant and Hessian convex away from
![]() $0$
. Then
$0$
. Then
![]() $Q=\partial \mathcal{D}/\Gamma$
is a compact, Hessian-convex, codimension-1 submanifold of
$Q=\partial \mathcal{D}/\Gamma$
is a compact, Hessian-convex, codimension-1 submanifold of
![]() $W$
. Let
$W$
. Let
![]() $K\subset \mathbb{RP}^{n+1}$
be the closure of
$K\subset \mathbb{RP}^{n+1}$
be the closure of
![]() $\mathcal{D}$
and regard
$\mathcal{D}$
and regard
![]() $\mathbb{RP}^{n+1}={\mathbb{R}}^{n+1}\sqcup \mathbb{RP}^n_{\infty }$
. The interior of
$\mathbb{RP}^{n+1}={\mathbb{R}}^{n+1}\sqcup \mathbb{RP}^n_{\infty }$
. The interior of
![]() $K\cap \mathbb{RP}^n_{\infty }$
can be identified with
$K\cap \mathbb{RP}^n_{\infty }$
can be identified with
![]() $\Omega$
. The existence of the hypersurface
$\Omega$
. The existence of the hypersurface
![]() $Q$
in
$Q$
in
![]() $W$
implies the existence of
$W$
implies the existence of
![]() $\mathcal{D}\subset {\mathbb{R}}^{n+1}$
, which implies
$\mathcal{D}\subset {\mathbb{R}}^{n+1}$
, which implies
![]() $\Omega$
is properly convex, by the reasoning above.
$\Omega$
is properly convex, by the reasoning above.
By the Ehresmann–Thurston principle, deforming
![]() $\Gamma$
a small amount to
$\Gamma$
a small amount to
![]() $\Gamma ^{\prime}$
gives a new projective
$\Gamma ^{\prime}$
gives a new projective
![]() $n$
-manifold
$n$
-manifold
![]() $M^{\prime}\cong M$
, and a new affine
$M^{\prime}\cong M$
, and a new affine
![]() $(n+1)$
-manifold
$(n+1)$
-manifold
![]() $W^{\prime}\cong M\times S^1$
. Now
$W^{\prime}\cong M\times S^1$
. Now
![]() $W^{\prime}$
contains a hypersurface
$W^{\prime}$
contains a hypersurface
![]() $Q^{\prime}$
that is Hessian convex, provided the deformation of the developing map is small enough in
$Q^{\prime}$
that is Hessian convex, provided the deformation of the developing map is small enough in
![]() $C^2$
. It then follows that
$C^2$
. It then follows that
![]() $M^{\prime}$
is properly convex. This is the approach taken in [Reference Cooper, Long and TillmannCLT18] for non-compact manifolds.
$M^{\prime}$
is properly convex. This is the approach taken in [Reference Cooper, Long and TillmannCLT18] for non-compact manifolds.
Here, we choose to work with a piecewise linear submanifold
![]() $Q$
in place of a smooth one. Hessian convexity is replaced by the condition that at each vertex of the triangulation the determinants, of certain matrices formed by the relative positions of vertices, are strictly positive. This ensures local convexity near the vertex. This version of convexity is preserved by small
$Q$
in place of a smooth one. Hessian convexity is replaced by the condition that at each vertex of the triangulation the determinants, of certain matrices formed by the relative positions of vertices, are strictly positive. This ensures local convexity near the vertex. This version of convexity is preserved by small
![]() $C^0$
-deformations of the developing map. Thus it is easier to apply. We start by reviewing these ideas for hyperbolic manifolds.
$C^0$
-deformations of the developing map. Thus it is easier to apply. We start by reviewing these ideas for hyperbolic manifolds.
The hyperboloid model of the hyperbolic plane is the action of
![]() ${\textrm {O}}(2,1)$
on the surface
${\textrm {O}}(2,1)$
on the surface
![]() $S\subset {\mathbb{R}}^3$
given by
$S\subset {\mathbb{R}}^3$
given by
![]() $x^2+y^2-z^2=-1$
. If we identify
$x^2+y^2-z^2=-1$
. If we identify
![]() ${\mathbb{R}}^3$
with
${\mathbb{R}}^3$
with
![]() $\mathbb{RP}^3\setminus \mathbb{RP}^2_{\infty }$
, then we can regard this as an affine action on
$\mathbb{RP}^3\setminus \mathbb{RP}^2_{\infty }$
, then we can regard this as an affine action on
![]() $\mathbb{RP}^3$
by using the affine subgroup
$\mathbb{RP}^3$
by using the affine subgroup
![]() ${\textrm {O}}(2,1)\oplus (1)\subset \textrm {SL}(4,{\mathbb{R}})$
. The open disc
${\textrm {O}}(2,1)\oplus (1)\subset \textrm {SL}(4,{\mathbb{R}})$
. The open disc
has the same frontier as
![]() $S$
, and
$S$
, and
![]() $({\textrm {O}}(2,1),D)$
is the projective (Klein) model of the hyperbolic plane. See Figure 7.
$({\textrm {O}}(2,1),D)$
is the projective (Klein) model of the hyperbolic plane. See Figure 7.

Figure 7. The hyperboloid and Klein models of
![]() ${\mathbb{H}}^2$
.
${\mathbb{H}}^2$
.
The surface
![]() $\textrm {cl}(S\cup D)\subset \mathbb{RP}^3$
bounds a closed
$\textrm {cl}(S\cup D)\subset \mathbb{RP}^3$
bounds a closed
![]() $3$
-ball
$3$
-ball
![]() $B\subset \mathbb{RP}^3$
. Let
$B\subset \mathbb{RP}^3$
. Let
![]() $\Omega =B\setminus \textrm {Fr} D\cong D\times I$
. The fact that
$\Omega =B\setminus \textrm {Fr} D\cong D\times I$
. The fact that
![]() $S$
is a strictly convex surface implies
$S$
is a strictly convex surface implies
![]() $\textrm {cl}(S\cup D)$
is a convex surface in some affine patch which implies
$\textrm {cl}(S\cup D)$
is a convex surface in some affine patch which implies
![]() $\Omega$
is properly convex, and this implies
$\Omega$
is properly convex, and this implies
![]() $D$
is properly convex. If one thinks of
$D$
is properly convex. If one thinks of
![]() $B$
as an upside down mountain, then the convexity of the surface
$B$
as an upside down mountain, then the convexity of the surface
![]() $S$
implies the convexity of
$S$
implies the convexity of
![]() $D$
.
$D$
.
The action of
![]() ${\textrm {O}}(2,1)\oplus (1)$
preserves
${\textrm {O}}(2,1)\oplus (1)$
preserves
![]() $\Omega$
. Suppose
$\Omega$
. Suppose
![]() $\Gamma \subset {\textrm {O}}(2,1)$
and
$\Gamma \subset {\textrm {O}}(2,1)$
and
![]() $\Sigma =D/\Gamma$
is a hyperbolic surface. Let
$\Sigma =D/\Gamma$
is a hyperbolic surface. Let
![]() $\Gamma ^{\prime}=\Gamma \oplus (1)$
, then
$\Gamma ^{\prime}=\Gamma \oplus (1)$
, then
![]() $N=\Omega /\Gamma ^{\prime}\cong \Sigma \times [0,1]$
is a properly convex 3-manifold with one flat boundary component
$N=\Omega /\Gamma ^{\prime}\cong \Sigma \times [0,1]$
is a properly convex 3-manifold with one flat boundary component
![]() $\Sigma =D/\Gamma$
and one strictly convex boundary component
$\Sigma =D/\Gamma$
and one strictly convex boundary component
![]() $M=S/\Gamma$
. The fact that
$M=S/\Gamma$
. The fact that
![]() $M$
is a strictly convex surface implies
$M$
is a strictly convex surface implies
![]() $\Sigma$
is properly convex. We will generalize this construction to arbitrary properly convex manifolds in place of
$\Sigma$
is properly convex. We will generalize this construction to arbitrary properly convex manifolds in place of
![]() $\Sigma$
. But first we divide out by a homothety.
$\Sigma$
. But first we divide out by a homothety.
Consider the cone
![]() $\mathcal{C}=\{\lambda \cdot x:x\in S,\ \ \lambda \gt 0\}$
. There is a product structure
$\mathcal{C}=\{\lambda \cdot x:x\in S,\ \ \lambda \gt 0\}$
. There is a product structure
![]() $\widetilde \phi :S\times {\mathbb{R}}^+ \to \mathcal{C}$
given by
$\widetilde \phi :S\times {\mathbb{R}}^+ \to \mathcal{C}$
given by
![]() $\widetilde \phi (x,\lambda )=\lambda \cdot x$
on
$\widetilde \phi (x,\lambda )=\lambda \cdot x$
on
![]() $\mathcal{C}$
that is preserved by
$\mathcal{C}$
that is preserved by
![]() $\Gamma ^{\prime}$
. Let
$\Gamma ^{\prime}$
. Let
![]() $H\subset \textrm {GL}(4,{\mathbb{R}})$
be the cyclic group generated by
$H\subset \textrm {GL}(4,{\mathbb{R}})$
be the cyclic group generated by
![]() $\textrm {Diag}(2,2,2,1)$
. Then
$\textrm {Diag}(2,2,2,1)$
. Then
![]() $\Gamma ^{\prime}$
centralizes
$\Gamma ^{\prime}$
centralizes
![]() $H$
and the group
$H$
and the group
![]() $\Gamma ^+\subset \textrm {GL}(4,{\mathbb{R}})$
generated by
$\Gamma ^+\subset \textrm {GL}(4,{\mathbb{R}})$
generated by
![]() $\Gamma ^{\prime}$
and
$\Gamma ^{\prime}$
and
![]() $H$
preserves
$H$
preserves
![]() $\mathcal{C}$
and
$\mathcal{C}$
and
![]() $W:=\mathcal{C}/\Gamma ^+$
is a closed
$W:=\mathcal{C}/\Gamma ^+$
is a closed
![]() $3$
-manifold homeomorphic to
$3$
-manifold homeomorphic to
![]() $\Sigma \times S^1$
.
$\Sigma \times S^1$
.
In what follows
![]() ${\mathbb{R}}^+=\{x\in {\mathbb{R}}:x\gt 0\}$
, and
${\mathbb{R}}^+=\{x\in {\mathbb{R}}:x\gt 0\}$
, and
![]() $S^1={\mathbb{R}}^+/\exp ({\mathbb{Z}})$
, has universal cover
$S^1={\mathbb{R}}^+/\exp ({\mathbb{Z}})$
, has universal cover
![]() ${\mathbb{R}}^+$
. There is a product structure
${\mathbb{R}}^+$
. There is a product structure
![]() $\phi :\Sigma \times S^1\to W$
covered by
$\phi :\Sigma \times S^1\to W$
covered by
![]() $\widetilde \phi$
, and the surfaces
$\widetilde \phi$
, and the surfaces
![]() $\phi (\Sigma ,\theta )$
are convex. The reader might contemplate all this in the case of one dimension lower, where
$\phi (\Sigma ,\theta )$
are convex. The reader might contemplate all this in the case of one dimension lower, where
![]() $\Gamma \subset {\textrm {SO}}(1,1)$
is generated by a hyperbolic and
$\Gamma \subset {\textrm {SO}}(1,1)$
is generated by a hyperbolic and
![]() $\mathcal{C}/\Gamma ^+$
is an affine structure on
$\mathcal{C}/\Gamma ^+$
is an affine structure on
![]() $S^1\times S^1$
.
$S^1\times S^1$
.
We now return to the general setting. The radiant-affine group is the subgroup of the affine group acting on
![]() ${\mathbb{R}}^n$
that fixes the origin
${\mathbb{R}}^n$
that fixes the origin
Radiant-affine geometry is
![]() $(\textrm {RA}(n),{\mathbb{R}}^n_0)$
and is a subgeometry of affine geometry, so we may use affine notions. It is also isomorphic to a subgeometry of projective geometry under the embedding
$(\textrm {RA}(n),{\mathbb{R}}^n_0)$
and is a subgeometry of affine geometry, so we may use affine notions. It is also isomorphic to a subgeometry of projective geometry under the embedding
The subgroup
![]() $t {\textrm {I}}_n\oplus 1$
with
$t {\textrm {I}}_n\oplus 1$
with
![]() $t\gt 0$
is called the homothety flow. This subgroup acts on
$t\gt 0$
is called the homothety flow. This subgroup acts on
![]() ${\mathbb{R}}^n_0$
by homotheties:
${\mathbb{R}}^n_0$
by homotheties:
![]() $x\mapsto t\cdot x$
. The quotient of the tautological line bundle by a cyclic group of homotheties is the tautological circle bundle over
$x\mapsto t\cdot x$
. The quotient of the tautological line bundle by a cyclic group of homotheties is the tautological circle bundle over
![]() $M$
.
$M$
.
Definition 3.3.
If
![]() $M$
is a closed
$M$
is a closed
![]() $(n-1)$
-manifold, then a tautological circle bundle structure on
$(n-1)$
-manifold, then a tautological circle bundle structure on
![]() $M\times S^1$
is a radiant-affine geometry structure
$M\times S^1$
is a radiant-affine geometry structure
![]() $(\textrm {dev},\rho )$
such that:
$(\textrm {dev},\rho )$
such that:
-
(i) the generator of
 $\pi _1(*\times S^1)$
acts on
$\pi _1(*\times S^1)$
acts on
 ${\mathbb{R}}^n_0$
by
${\mathbb{R}}^n_0$
by
 $x\mapsto 2 x$
;
$x\mapsto 2 x$
; -
(ii)
 $\det (\rho \pi _1(M\times 1))\subset \{\pm 1\}$
.
$\det (\rho \pi _1(M\times 1))\subset \{\pm 1\}$
.
Let
![]() $\pi :{\mathbb{R}}^n_0\rightarrow S^{n-1}$
be radial projection
$\pi :{\mathbb{R}}^n_0\rightarrow S^{n-1}$
be radial projection
![]() $\pi (x)=x/\|x\|$
. The second condition implies that
$\pi (x)=x/\|x\|$
. The second condition implies that
is a positive projective structure on
![]() $M$
. Conversely a positive projective structure on
$M$
. Conversely a positive projective structure on
![]() $M$
determines a radiant-affine geometry structure on
$M$
determines a radiant-affine geometry structure on
![]() $M\times S^1$
. Multiplication by
$M\times S^1$
. Multiplication by
![]() $S^1$
on the right factor of
$S^1$
on the right factor of
![]() $W=M\times S^1$
corresponds by the developing map to homotheties. We call all of these actions homothety or the radial flow.
$W=M\times S^1$
corresponds by the developing map to homotheties. We call all of these actions homothety or the radial flow.
Suppose
![]() $W$
is an affine
$W$
is an affine
![]() $n$
-manifold, and
$n$
-manifold, and
![]() $S$
is a hypersurface in
$S$
is a hypersurface in
![]() $W$
. Then
$W$
. Then
![]() $S$
is a convex hypersurface, and it is locally convex, if for every point
$S$
is a convex hypersurface, and it is locally convex, if for every point
![]() $p\in S$
there is an
$p\in S$
there is an
![]() $n$
-dimensional submanifold
$n$
-dimensional submanifold
![]() $Q\subset W$
with
$Q\subset W$
with
![]() $Q\cong \partial Q\times [0,1)$
and
$Q\cong \partial Q\times [0,1)$
and
![]() $\partial Q\subset S$
, and
$\partial Q\subset S$
, and
![]() $\partial Q$
is a neighborhood of
$\partial Q$
is a neighborhood of
![]() $p$
in
$p$
in
![]() $S$
and
$S$
and
![]() $\textrm {dev}(U)\subset {\mathbb{R}}^n$
is convex. If
$\textrm {dev}(U)\subset {\mathbb{R}}^n$
is convex. If
![]() $W=M\times S^1$
is a tautological circle bundle, then such
$W=M\times S^1$
is a tautological circle bundle, then such
![]() $S$
is outwards convex if, in addition,
$S$
is outwards convex if, in addition,
![]() $t\cdot \partial Q\cap Q\ne \emptyset$
for some
$t\cdot \partial Q\cap Q\ne \emptyset$
for some
![]() $t\gt 1$
. In other words
$t\gt 1$
. In other words
![]() $\textrm {dev}\widetilde S$
is locally convex away from
$\textrm {dev}\widetilde S$
is locally convex away from
![]() $0$
in
$0$
in
![]() ${\mathbb{R}}^{n+1}$
.
${\mathbb{R}}^{n+1}$
.
A locally convex hypersurface
![]() $S$
is strictly convex if every connected flat subset of
$S$
is strictly convex if every connected flat subset of
![]() $S$
is a single point. If, instead, every connected flat subset of
$S$
is a single point. If, instead, every connected flat subset of
![]() $\widetilde S$
is contained in a compact set, then
$\widetilde S$
is contained in a compact set, then
![]() $S$
is called strongly convex. We will make use of strongly convex when
$S$
is called strongly convex. We will make use of strongly convex when
![]() $S$
has a triangulation by flat simplices, no two of which are in the same hyperplane. In this case
$S$
has a triangulation by flat simplices, no two of which are in the same hyperplane. In this case
![]() $S$
is called simplicial convex.
$S$
is called simplicial convex.
Definition 3.4.
A tautological circle bundle structure on
![]() $M\times S^1$
is radial convex if
$M\times S^1$
is radial convex if
![]() $M\times \theta$
is an outwards strongly-convex hypersurface in
$M\times \theta$
is an outwards strongly-convex hypersurface in
![]() $M\times S^1$
for some (and hence all)
$M\times S^1$
for some (and hence all)
![]() $\theta \in S^1$
.
$\theta \in S^1$
.
Theorem 3.5.
If
![]() $M\times S^1$
is compact and radial convex, then the associated projective structure on
$M\times S^1$
is compact and radial convex, then the associated projective structure on
![]() $M$
is properly convex.
$M$
is properly convex.
Proof.
Let
![]() $n=\dim M$
. In this proof we consider the image of several sets under the developing map and use the notation
$n=\dim M$
. In this proof we consider the image of several sets under the developing map and use the notation
![]() $X=\textrm {dev}(X^{\prime})$
.
$X=\textrm {dev}(X^{\prime})$
.
Let
![]() $N=M\times S^1$
and
$N=M\times S^1$
and
![]() $\pi _{_{N^{\prime}}}:\widetilde N^{\prime}=\widetilde M\times {\mathbb{R}}^+\rightarrow N$
be the universal cover, and
$\pi _{_{N^{\prime}}}:\widetilde N^{\prime}=\widetilde M\times {\mathbb{R}}^+\rightarrow N$
be the universal cover, and
![]() $\textrm {dev}:\widetilde N^{\prime}\rightarrow {\mathbb{R}}^{n+1}_0$
the developing map for
$\textrm {dev}:\widetilde N^{\prime}\rightarrow {\mathbb{R}}^{n+1}_0$
the developing map for
![]() $N$
. Let
$N$
. Let
![]() $R^{\prime}=\widetilde M\times t$
for some
$R^{\prime}=\widetilde M\times t$
for some
![]() $t\gt 0$
, and choose a basepoint
$t\gt 0$
, and choose a basepoint
![]() $p^{\prime}\in R^{\prime}$
. Let
$p^{\prime}\in R^{\prime}$
. Let
![]() $V\subset {\mathbb{R}}^{n+1}$
be a two-dimensional vector subspace that contains
$V\subset {\mathbb{R}}^{n+1}$
be a two-dimensional vector subspace that contains
![]() $p=\textrm {dev}(p^{\prime})$
. Since
$p=\textrm {dev}(p^{\prime})$
. Since
![]() $V$
is preserved by homothety,
$V$
is preserved by homothety,
![]() $\textrm {dev}^{-1}V = X\times {\mathbb{R}}^+$
for some
$\textrm {dev}^{-1}V = X\times {\mathbb{R}}^+$
for some
![]() $1$
-submanifold
$1$
-submanifold
![]() $X\subset \widetilde M$
. Let
$X\subset \widetilde M$
. Let
![]() $C^{\prime}$
be the component of
$C^{\prime}$
be the component of
![]() $R^{\prime}\cap \textrm {dev}^{-1}V$
that contains
$R^{\prime}\cap \textrm {dev}^{-1}V$
that contains
![]() $p^{\prime}$
. Then
$p^{\prime}$
. Then
![]() $C^{\prime}$
is a connected curve in
$C^{\prime}$
is a connected curve in
![]() $\textrm {dev}^{-1}V$
without endpoints that is transverse to the homothety flow and convex outwards.
$\textrm {dev}^{-1}V$
without endpoints that is transverse to the homothety flow and convex outwards.
The curve
![]() $C=\textrm {dev}(C^{\prime})$
is immersed in
$C=\textrm {dev}(C^{\prime})$
is immersed in
![]() $V_0$
, contains
$V_0$
, contains
![]() $p$
, is everywhere transverse to the radial direction, and convex outwards: radially away from
$p$
, is everywhere transverse to the radial direction, and convex outwards: radially away from
![]() $0$
.
$0$
.
Claim 1:
![]() $\textrm {dev}|C^{\prime}$
is injective.
$\textrm {dev}|C^{\prime}$
is injective.
Let
![]() $\pi :V_0\to S^1$
be radial projection
$\pi :V_0\to S^1$
be radial projection
![]() $\pi (x)=x/\|x\|$
. We show that
$\pi (x)=x/\|x\|$
. We show that
![]() $\theta =\pi \circ \textrm {dev}:C^{\prime}\to S^1$
is injective. Since
$\theta =\pi \circ \textrm {dev}:C^{\prime}\to S^1$
is injective. Since
![]() $C^{\prime}$
is transverse to the radial direction in
$C^{\prime}$
is transverse to the radial direction in
![]() $\widetilde N^{\prime}$
, it follows that
$\widetilde N^{\prime}$
, it follows that
![]() $\theta$
is an immersion. Let
$\theta$
is an immersion. Let
![]() $\ell \subset V$
be the tangent line to
$\ell \subset V$
be the tangent line to
![]() $C$
at
$C$
at
![]() $p$
. Suppose
$p$
. Suppose
![]() $q\in C\cap \ell$
is distinct from
$q\in C\cap \ell$
is distinct from
![]() $p$
. Then at some point
$p$
. Then at some point
![]() $r$
in
$r$
in
![]() $C$
between
$C$
between
![]() $p$
and
$p$
and
![]() $q$
, the distance of
$q$
, the distance of
![]() $r$
from
$r$
from
![]() $\ell$
is a maximum. This contradicts that
$\ell$
is a maximum. This contradicts that
![]() $C$
is convex outwards at
$C$
is convex outwards at
![]() $r$
. Hence
$r$
. Hence
![]() $\pi (\ell )$
is an open semi-circle in
$\pi (\ell )$
is an open semi-circle in
![]() $S^1$
that contains
$S^1$
that contains
![]() $\pi (C)$
. Thus
$\pi (C)$
. Thus
![]() $\theta$
is an immersion of
$\theta$
is an immersion of
![]() $C^{\prime}$
into this arc, therefore
$C^{\prime}$
into this arc, therefore
![]() $\theta$
is injective, and it follows that
$\theta$
is injective, and it follows that
![]() $\pi$
is injective. This proves Claim 1.
$\pi$
is injective. This proves Claim 1.
Claim 2:
![]() $C$
is a closed subset of
$C$
is a closed subset of
![]() $V$
.
$V$
.
Otherwise
![]() $C$
limits on a point
$C$
limits on a point
![]() $w$
in
$w$
in
![]() $V$
. Let
$V$
. Let
![]() $\widetilde \kappa :[0,1)\rightarrow V$
be an affine map with image
$\widetilde \kappa :[0,1)\rightarrow V$
be an affine map with image
![]() $[p,w)$
. Refer to Figure 8. Now
$[p,w)$
. Refer to Figure 8. Now
![]() $C^{\prime}\times {\mathbb{R}}^+\subset \widetilde N^{\prime}$
so there is an affine ray
$C^{\prime}\times {\mathbb{R}}^+\subset \widetilde N^{\prime}$
so there is an affine ray
![]() $\widetilde \kappa ^{\prime}:[0,1)\rightarrow C^{\prime}\times {\mathbb{R}}^+$
with
$\widetilde \kappa ^{\prime}:[0,1)\rightarrow C^{\prime}\times {\mathbb{R}}^+$
with
![]() $\kappa =\textrm {dev}\circ \widetilde \kappa ^{\prime}$
that starts at
$\kappa =\textrm {dev}\circ \widetilde \kappa ^{\prime}$
that starts at
![]() $\widetilde \kappa ^{\prime}(0)=p^{\prime}$
. This ray leaves every compact set in
$\widetilde \kappa ^{\prime}(0)=p^{\prime}$
. This ray leaves every compact set in
![]() $\widetilde N^{\prime}$
, since otherwise it can be extended, and this would extend
$\widetilde N^{\prime}$
, since otherwise it can be extended, and this would extend
![]() $C^{\prime}$
. Thus
$C^{\prime}$
. Thus
![]() $\kappa ^{\prime}=\pi _{_{N^{\prime}}}\circ \widetilde \kappa ^{\prime}:[0,1)\rightarrow N$
spirals in towards, and accumulates on, some subset
$\kappa ^{\prime}=\pi _{_{N^{\prime}}}\circ \widetilde \kappa ^{\prime}:[0,1)\rightarrow N$
spirals in towards, and accumulates on, some subset
![]() $F$
of
$F$
of
![]() $M\times t\subset N$
. In other words
$M\times t\subset N$
. In other words
![]() $F$
is the forward limit set of
$F$
is the forward limit set of
![]() $\kappa ^{\prime}$
. To justify this, in Figure 8 the ray
$\kappa ^{\prime}$
. To justify this, in Figure 8 the ray
![]() $\widetilde \kappa$
approaches
$\widetilde \kappa$
approaches
![]() $C$
in
$C$
in
![]() $V$
. However in
$V$
. However in
![]() $N$
the ray
$N$
the ray
![]() $\kappa ^{\prime}$
has infinite length. Choose a product metric on
$\kappa ^{\prime}$
has infinite length. Choose a product metric on
![]() $N=M\times S^1$
. The universal cover of
$N=M\times S^1$
. The universal cover of
![]() $S^1$
is
$S^1$
is
![]() ${\mathbb{R}}^+$
and we use the metric on
${\mathbb{R}}^+$
and we use the metric on
![]() ${\mathbb{R}}^+$
given by
${\mathbb{R}}^+$
given by
![]() $d(a,b)=|\log (a/b)|$
. From Figure 8 one can see the distance in
$d(a,b)=|\log (a/b)|$
. From Figure 8 one can see the distance in
![]() $N$
of points on
$N$
of points on
![]() $\kappa ^{\prime}$
from
$\kappa ^{\prime}$
from
![]() $M\times t$
in the
$M\times t$
in the
![]() $S^1$
direction goes to
$S^1$
direction goes to
![]() $0$
.
$0$
.
Now
![]() $F$
is flat because
$F$
is flat because
![]() $\kappa ^{\prime}$
is affine. The closure of some component of
$\kappa ^{\prime}$
is affine. The closure of some component of
![]() $\pi _{_{N^{\prime}}}^{-1}(F)$
in
$\pi _{_{N^{\prime}}}^{-1}(F)$
in
![]() $\widetilde N^{\prime}$
is not compact, otherwise
$\widetilde N^{\prime}$
is not compact, otherwise
![]() $\kappa ^{\prime}$
converges to a limit point in
$\kappa ^{\prime}$
converges to a limit point in
![]() $F$
that maps to
$F$
that maps to
![]() $w$
. This contradicts that
$w$
. This contradicts that
![]() $M\times t$
is strongly locally convex, and thus contradicts that
$M\times t$
is strongly locally convex, and thus contradicts that
![]() $M\times S^1$
is radial convex. This proves Claim 2.
$M\times S^1$
is radial convex. This proves Claim 2.
Thus every point in
![]() $R^{\prime}$
is connected to
$R^{\prime}$
is connected to
![]() $p^{\prime}$
by some segment in
$p^{\prime}$
by some segment in
![]() $\widetilde N^{\prime}$
. Using the radial flow it follows that
$\widetilde N^{\prime}$
. Using the radial flow it follows that
![]() $\widetilde N^{\prime}$
is starshaped from
$\widetilde N^{\prime}$
is starshaped from
![]() $p^{\prime}$
. But
$p^{\prime}$
. But
![]() $p^{\prime}$
was arbitrary, so
$p^{\prime}$
was arbitrary, so
![]() $\widetilde N^{\prime}$
is convex. Hence
$\widetilde N^{\prime}$
is convex. Hence
![]() $\textrm {dev}:\widetilde N^{\prime}\rightarrow {\mathbb{R}}^{n+1}_0$
is injective. Moreover since
$\textrm {dev}:\widetilde N^{\prime}\rightarrow {\mathbb{R}}^{n+1}_0$
is injective. Moreover since
![]() $\kappa$
lies above
$\kappa$
lies above
![]() $C$
it follows that
$C$
it follows that
![]() $\ X=\textrm {dev}(\widetilde M\times [1,\infty ))$
is convex. Now
$\ X=\textrm {dev}(\widetilde M\times [1,\infty ))$
is convex. Now
![]() $\partial X=\textrm {dev}(\widetilde M\times 1)$
is a properly embedded convex hypersurface in
$\partial X=\textrm {dev}(\widetilde M\times 1)$
is a properly embedded convex hypersurface in
![]() ${\mathbb{R}}^{n+1}$
. Thus
${\mathbb{R}}^{n+1}$
. Thus
![]() $X$
is properly convex in
$X$
is properly convex in
![]() $\mathbb{RP}^{n+1}$
. Let
$\mathbb{RP}^{n+1}$
. Let
![]() $Y$
be the closure of
$Y$
be the closure of
![]() $X$
in
$X$
in
![]() $\mathbb{RP}^{n+1}$
. Then
$\mathbb{RP}^{n+1}$
. Then
![]() $Y$
is properly convex and it follows that
$Y$
is properly convex and it follows that
![]() $\mathbb{RP}^n_{\infty }\cap Y$
is properly convex. Now
$\mathbb{RP}^n_{\infty }\cap Y$
is properly convex. Now
![]() $Y$
is the image of the projective structure on
$Y$
is the image of the projective structure on
![]() $M$
under the developing map into
$M$
under the developing map into
![]() $\mathbb{RP}^n_{\infty }$
. Hence
$\mathbb{RP}^n_{\infty }$
. Hence
![]() $M$
is properly convex.
$M$
is properly convex.

Figure 8. The case of
![]() $\widetilde \kappa$
in
$\widetilde \kappa$
in
![]() $V$
.
$V$
.
If
![]() $W$
is affine, then a hypersurface,
$W$
is affine, then a hypersurface,
![]() $S\subset W$
, is simplicial if it has a triangulation by flat simplices. If
$S\subset W$
, is simplicial if it has a triangulation by flat simplices. If
![]() $S$
is locally convex and simplicial, and every connected flat subset of
$S$
is locally convex and simplicial, and every connected flat subset of
![]() $S$
is contained in a simplex in
$S$
is contained in a simplex in
![]() $S$
, then
$S$
, then
![]() $S$
is called simplicial convex. These are a substitute for strictly convex. Observe that a locally convex simplicial surface is simplicial convex if and only if adjacent simplices the same dimension as
$S$
is called simplicial convex. These are a substitute for strictly convex. Observe that a locally convex simplicial surface is simplicial convex if and only if adjacent simplices the same dimension as
![]() $S$
are never in the same hyperplane.
$S$
are never in the same hyperplane.
Lemma 3.6.
Suppose that
![]() $S$
is a simplicial convex hypersurface in an affine
$S$
is a simplicial convex hypersurface in an affine
![]() $n$
-manifold
$n$
-manifold
![]() $W$
. Then for each vertex
$W$
. Then for each vertex
![]() $v$
of
$v$
of
![]() $S$
, there is a neighborhood
$S$
, there is a neighborhood
![]() $U(v)$
, such that the hypersurface
$U(v)$
, such that the hypersurface
![]() $S^{\prime}$
obtained by moving each vertex
$S^{\prime}$
obtained by moving each vertex
![]() $v$
inside
$v$
inside
![]() $U(v)$
is simplicial convex.
$U(v)$
is simplicial convex.
Proof.
This is a local question, so we assume
![]() $W={\mathbb{R}}^n$
. The general case follows using the developing map. The simplicial convex condition at the vertex
$W={\mathbb{R}}^n$
. The general case follows using the developing map. The simplicial convex condition at the vertex
![]() $v$
is equivalent to the positivity of the determinants of certain
$v$
is equivalent to the positivity of the determinants of certain
![]() $n\times n$
matrices formed by vectors of the form
$n\times n$
matrices formed by vectors of the form
![]() $u-v$
for certain vertices,
$u-v$
for certain vertices,
![]() $u$
, that are adjacent to
$u$
, that are adjacent to
![]() $v$
in
$v$
in
![]() $S$
. If the vertices of
$S$
. If the vertices of
![]() $S$
are moved a small enough distance, these determinants remain positive. Thus
$S$
are moved a small enough distance, these determinants remain positive. Thus
![]() $S^{\prime}$
is simplicial convex. Now we explain the determinant condition.
$S^{\prime}$
is simplicial convex. Now we explain the determinant condition.
Let
![]() $K$
be the union of the simplices in
$K$
be the union of the simplices in
![]() $S$
that contain
$S$
that contain
![]() $v$
. Suppose
$v$
. Suppose
![]() $\sigma$
is a simplex in
$\sigma$
is a simplex in
![]() $K$
of dimension
$K$
of dimension
![]() $(n-1)$
. Then
$(n-1)$
. Then
![]() $\sigma$
is contained in a hyperplane
$\sigma$
is contained in a hyperplane
![]() $H$
. If
$H$
. If
![]() $K$
is simplicial convex, then all of
$K$
is simplicial convex, then all of
![]() $K$
is on one side of
$K$
is on one side of
![]() $H$
.
$H$
.
Conversely,
![]() $S$
is simplicial convex at
$S$
is simplicial convex at
![]() $v$
if this condition holds for each such
$v$
if this condition holds for each such
![]() $\sigma$
. Let
$\sigma$
. Let
![]() $\{v_0,\cdots ,v_{n-1}\}$
be the vertices of
$\{v_0,\cdots ,v_{n-1}\}$
be the vertices of
![]() $\sigma$
. Let
$\sigma$
. Let
![]() $f(u)=\det (v_0-u:v_1-u:\cdots :v_{n-1}-u)$
. The condition for simplicial convexity is that the sign of
$f(u)=\det (v_0-u:v_1-u:\cdots :v_{n-1}-u)$
. The condition for simplicial convexity is that the sign of
![]() $f(u)$
is constant as
$f(u)$
is constant as
![]() $u$
ranges over all vertices in
$u$
ranges over all vertices in
![]() $K$
that are connected by an edge to
$K$
that are connected by an edge to
![]() $\sigma$
and that are not in
$\sigma$
and that are not in
![]() $\sigma$
. This ensures the simplices adjacent to
$\sigma$
. This ensures the simplices adjacent to
![]() $\sigma$
in
$\sigma$
in
![]() $K$
all lie on the same side of the hyperplane that contains
$K$
all lie on the same side of the hyperplane that contains
![]() $\sigma$
.
$\sigma$
.
The convex hull,
![]() $\textrm {CH}(Y)$
, of
$\textrm {CH}(Y)$
, of
![]() $Y\subset {\mathbb{R}}^n$
is the intersection of all the closed convex sets that contain
$Y\subset {\mathbb{R}}^n$
is the intersection of all the closed convex sets that contain
![]() $Y$
. Let
$Y$
. Let
![]() $\pi _{\xi }:V_0\to {\mathbb{P}}_+(V)$
be the projection
$\pi _{\xi }:V_0\to {\mathbb{P}}_+(V)$
be the projection
![]() $\pi _{\xi }(x)=[x]_+$
. The next result can also be proven by using the existence of an affine sphere [Reference Cheng and YauCY77, Reference LoftinLof10].
$\pi _{\xi }(x)=[x]_+$
. The next result can also be proven by using the existence of an affine sphere [Reference Cheng and YauCY77, Reference LoftinLof10].
Theorem 3.7.
Suppose
![]() $\mathcal{C}\subset {\mathbb{R}}^{n+1}$
is a convex cone,
$\mathcal{C}\subset {\mathbb{R}}^{n+1}$
is a convex cone,
![]() $\Omega =\pi _{\xi }(\mathcal{C})\subset \mathbb{RP}_+^n$
and
$\Omega =\pi _{\xi }(\mathcal{C})\subset \mathbb{RP}_+^n$
and
![]() $M=\Omega /\Gamma$
is a properly convex closed manifold.
$M=\Omega /\Gamma$
is a properly convex closed manifold.
Then there is a convex proper submanifold
![]() $P\subset \mathcal{C}$
with
$P\subset \mathcal{C}$
with
![]() $t\cdot P\subset P$
for all
$t\cdot P\subset P$
for all
![]() $t\geqslant 1$
, and
$t\geqslant 1$
, and
![]() $(\pi _{\xi }|\partial P):\partial P\to \Omega$
is a homeomorphism. Moreover,
$(\pi _{\xi }|\partial P):\partial P\to \Omega$
is a homeomorphism. Moreover,
![]() $P$
can be chosen such that
$P$
can be chosen such that
![]() $\partial P/\Gamma \subset \mathcal{C}/\Gamma$
is a compact, simplicial convex, simplicial hypersurface.
$\partial P/\Gamma \subset \mathcal{C}/\Gamma$
is a compact, simplicial convex, simplicial hypersurface.
Proof.
Let
![]() $\mathcal{D}\subset \mathcal{C}$
be the closed convex subset given by (2.1). Then
$\mathcal{D}\subset \mathcal{C}$
be the closed convex subset given by (2.1). Then
![]() $N=\mathcal{D}/\Gamma$
is a convex submanifold of
$N=\mathcal{D}/\Gamma$
is a convex submanifold of
![]() $\mathcal{C}/\Gamma$
with boundary a strictly convex hypersurface. Let
$\mathcal{C}/\Gamma$
with boundary a strictly convex hypersurface. Let
![]() $H\subset {\mathbb{R}}^{n+1}$
be an affine hyperplane that separates
$H\subset {\mathbb{R}}^{n+1}$
be an affine hyperplane that separates
![]() $\mathcal{D}$
into two components, such that the bounded component,
$\mathcal{D}$
into two components, such that the bounded component,
![]() $Y$
, projects to a subset
$Y$
, projects to a subset
![]() $\pi (Y)\subset N$
that is contained in a small ball in
$\pi (Y)\subset N$
that is contained in a small ball in
![]() $N$
. Replace
$N$
. Replace
![]() $N$
by
$N$
by
![]() $N\setminus \pi (Y)$
. This produces a flat part in the boundary. This can be done finitely many times, to produce a submanifold
$N\setminus \pi (Y)$
. This produces a flat part in the boundary. This can be done finitely many times, to produce a submanifold
![]() $Q\subset N$
with simplicial boundary. The preimage of
$Q\subset N$
with simplicial boundary. The preimage of
![]() $Q$
in
$Q$
in
![]() $\mathcal{C}$
is the required submanifold
$\mathcal{C}$
is the required submanifold
![]() $P$
.
$P$
.
Corollary 3.8.
A closed manifold
![]() $M$
is properly convex if and only if the tautological circle bundle
$M$
is properly convex if and only if the tautological circle bundle
![]() $M\times S^1$
is radial convex.
$M\times S^1$
is radial convex.
Corollary 3.9 [Reference LeeLee16]. A closed properly convex manifold
![]() $\Omega /\Gamma$
has a convex polyhedral fundamental domain in
$\Omega /\Gamma$
has a convex polyhedral fundamental domain in
![]() $\Omega$
.
$\Omega$
.
Proof.
Use the notation in the proof of (3.7). Let
![]() $H$
be a closed half-space that contains
$H$
be a closed half-space that contains
![]() $\mathcal{D}$
and such that
$\mathcal{D}$
and such that
![]() $(\partial \mathcal{D})\cap \partial H$
is a single point. Let
$(\partial \mathcal{D})\cap \partial H$
is a single point. Let
![]() $Y=\cap (\gamma \cdot H)$
where the intersection is over all
$Y=\cap (\gamma \cdot H)$
where the intersection is over all
![]() $\gamma \in \Gamma$
. Then
$\gamma \in \Gamma$
. Then
![]() $\mathcal{D}\subset Y\subset \mathcal{C}\Omega$
, and
$\mathcal{D}\subset Y\subset \mathcal{C}\Omega$
, and
![]() $Q=Y\cap \partial H$
is a convex polytope. Moreover
$Q=Y\cap \partial H$
is a convex polytope. Moreover
![]() $\partial Y=\Gamma \cdot Q$
is a locally finite union of images of
$\partial Y=\Gamma \cdot Q$
is a locally finite union of images of
![]() $Q$
. It follows that
$Q$
. It follows that
![]() $\pi _{\xi }(Q)$
is a convex polyhedral fundamental domain.
$\pi _{\xi }(Q)$
is a convex polyhedral fundamental domain.
Proof of Open Theorem 1. Suppose
![]() $\rho _0\in \textrm {Rep}_P(M)$
. This has a tautological circle bundle
$\rho _0\in \textrm {Rep}_P(M)$
. This has a tautological circle bundle
![]() $M\times S^1$
. Choose a triangulation of
$M\times S^1$
. Choose a triangulation of
![]() $M\times S^1$
so that
$M\times S^1$
so that
![]() $M\times 1$
is a simplicial convex hypersurface. If
$M\times 1$
is a simplicial convex hypersurface. If
![]() $\rho \in \textrm {Rep}_P(M)$
is close enough to
$\rho \in \textrm {Rep}_P(M)$
is close enough to
![]() $\rho _0$
, then (3.1) gives a nearby projective structure
$\rho _0$
, then (3.1) gives a nearby projective structure
![]() $M_{\rho }$
with holonomy
$M_{\rho }$
with holonomy
![]() $\rho$
so there is a nearby tautological circle bundle
$\rho$
so there is a nearby tautological circle bundle
![]() $M_{\rho }\times S^1$
for this projective structure. Moreover since the vertices have only been moved a small amount, (3.6) implies that
$M_{\rho }\times S^1$
for this projective structure. Moreover since the vertices have only been moved a small amount, (3.6) implies that
![]() $M_{\rho }\times 1$
is simplicial convex in this structure, so
$M_{\rho }\times 1$
is simplicial convex in this structure, so
![]() $M_{\rho }\times S^1$
is radial convex. By (3.5) the projective structure
$M_{\rho }\times S^1$
is radial convex. By (3.5) the projective structure
![]() $M_{\rho }$
is a properly convex structure. Thus
$M_{\rho }$
is a properly convex structure. Thus
![]() $\rho \in \textrm {Rep}_P(M)$
.
$\rho \in \textrm {Rep}_P(M)$
.
4. Closed
Here is an outline of the proof of the Closed Theorem. Suppose
![]() $\rho _k$
is a sequence of holonomies of properly convex real-projective structures on
$\rho _k$
is a sequence of holonomies of properly convex real-projective structures on
![]() $M$
, so that
$M$
, so that
![]() $M\cong \Omega _k/\rho _k(\pi _1M)$
with
$M\cong \Omega _k/\rho _k(\pi _1M)$
with
![]() $\Omega _k$
properly convex. Suppose the holonomies converge pointwise to
$\Omega _k$
properly convex. Suppose the holonomies converge pointwise to
![]() $\lim \rho _k=\rho _{\infty }$
. If
$\lim \rho _k=\rho _{\infty }$
. If
![]() $M$
is strictly convex, a special case of Chuckrow’s theorem (4.2) implies
$M$
is strictly convex, a special case of Chuckrow’s theorem (4.2) implies
![]() $\rho _{\infty }$
is discrete and faithful; in general
$\rho _{\infty }$
is discrete and faithful; in general
![]() $\rho _{\infty }$
is neither. After taking a subsequence we may assume
$\rho _{\infty }$
is neither. After taking a subsequence we may assume
![]() $\Omega _{\infty }=\lim \Omega _k\subset {\mathbb{RP}}^n$
exists. If
$\Omega _{\infty }=\lim \Omega _k\subset {\mathbb{RP}}^n$
exists. If
![]() $\Omega _{\infty }$
is properly convex, then
$\Omega _{\infty }$
is properly convex, then
![]() $\Omega _{\infty }/\rho _{\infty }(\pi _1M)$
is a properly convex structure on
$\Omega _{\infty }/\rho _{\infty }(\pi _1M)$
is a properly convex structure on
![]() $M$
. But
$M$
. But
![]() $\Omega _{\infty }$
might have smaller dimension, or it might not be properly convex. We describe this by saying the domain has degenerated.
$\Omega _{\infty }$
might have smaller dimension, or it might not be properly convex. We describe this by saying the domain has degenerated.
An example of this is provided by a sequence of properly convex projective structures on a torus given by
![]() $\Delta /\Gamma _n$
, where
$\Delta /\Gamma _n$
, where
![]() $\Delta$
is the interior of a triangle and
$\Delta$
is the interior of a triangle and
![]() $\Gamma _n\cong {\mathbb{Z}}^2$
is a discrete group of diagonal matrices (using a basis given by the vertices of
$\Gamma _n\cong {\mathbb{Z}}^2$
is a discrete group of diagonal matrices (using a basis given by the vertices of
![]() $\Delta$
) generated by
$\Delta$
) generated by
![]() $\alpha _n$
and
$\alpha _n$
and
![]() $\beta _n$
and
$\beta _n$
and
![]() $\alpha _n,\beta _n\to {\textrm {I}}$
. There are conjugates of these groups that converge to a discrete group acting on the plane, and the quotient is a Euclidean torus that is not properly convex.
$\alpha _n,\beta _n\to {\textrm {I}}$
. There are conjugates of these groups that converge to a discrete group acting on the plane, and the quotient is a Euclidean torus that is not properly convex.
The box estimate (4.3) implies that one may replace the original sequence
![]() $\rho _k$
by conjugates
$\rho _k$
by conjugates
![]() $\rho ^{\prime}_k$
which preserve domains
$\rho ^{\prime}_k$
which preserve domains
![]() $\Omega ^{\prime}_k$
and
$\Omega ^{\prime}_k$
and
![]() $\lim \rho _k^{\prime}=\sigma$
, and
$\lim \rho _k^{\prime}=\sigma$
, and
![]() $\lim \Omega ^{\prime}_k=\Omega$
is properly convex. Then
$\lim \Omega ^{\prime}_k=\Omega$
is properly convex. Then
![]() $N=\Omega /\sigma (\pi _1M)$
is a properly convex manifold homotopy equivalent to
$N=\Omega /\sigma (\pi _1M)$
is a properly convex manifold homotopy equivalent to
![]() $M$
. Hence
$M$
. Hence
![]() $N$
is closed and
$N$
is closed and
![]() $\pi _1M\cong \pi _1N$
. Also
$\pi _1M\cong \pi _1N$
. Also
![]() $N$
is strictly convex by (1.11). Finally,
$N$
is strictly convex by (1.11). Finally,
![]() $\sigma$
is irreducible by (4.1), which implies that, in fact, the original domains
$\sigma$
is irreducible by (4.1), which implies that, in fact, the original domains
![]() $\Omega _k$
did not degenerate. Thus
$\Omega _k$
did not degenerate. Thus
![]() $\rho _{\infty }$
is the holonomy of a strictly convex structure on
$\rho _{\infty }$
is the holonomy of a strictly convex structure on
![]() $M$
.
$M$
.
We supply the missing details, starting with the algebraic preliminaries.
Theorem 4.1 (Irreducible). Suppose
![]() $M=\Omega /\Gamma$
is a strictly convex closed manifold and
$M=\Omega /\Gamma$
is a strictly convex closed manifold and
![]() $\dim M\geqslant 2$
. Then
$\dim M\geqslant 2$
. Then
![]() $\Gamma$
does not preserve any proper projective subspace.
$\Gamma$
does not preserve any proper projective subspace.
Proof.
Suppose
![]() ${\mathbb{R}}^{n+1}=U\oplus V$
with
${\mathbb{R}}^{n+1}=U\oplus V$
with
![]() $U\ne 0\ne V$
and
$U\ne 0\ne V$
and
![]() $\Gamma \subset \textrm {GL}(n+1,{\mathbb{R}})$
preserves
$\Gamma \subset \textrm {GL}(n+1,{\mathbb{R}})$
preserves
![]() $U$
. Then
$U$
. Then
![]() $\Gamma$
preserves
$\Gamma$
preserves
![]() $Y=\textrm {cl}\Omega \cap {\mathbb{P}}_+ U$
. Now
$Y=\textrm {cl}\Omega \cap {\mathbb{P}}_+ U$
. Now
![]() $Y\cap \Omega = \emptyset$
by (1.14). Suppose
$Y\cap \Omega = \emptyset$
by (1.14). Suppose
![]() $Y=\emptyset$
. By the hyperplane separation theorem, there is
$Y=\emptyset$
. By the hyperplane separation theorem, there is
![]() $\phi \in ({\mathbb{R}}^{n+1})^*$
such that
$\phi \in ({\mathbb{R}}^{n+1})^*$
such that
![]() $\ker \phi$
contains
$\ker \phi$
contains
![]() $U$
, and
$U$
, and
![]() $\phi (\textrm {cl}\Omega )\gt 0$
. Thus
$\phi (\textrm {cl}\Omega )\gt 0$
. Thus
![]() $[\phi ]\in ({\mathbb{P}}_+ U^0)\cap \Omega ^*$
. By (2.6) the dual manifold
$[\phi ]\in ({\mathbb{P}}_+ U^0)\cap \Omega ^*$
. By (2.6) the dual manifold
![]() $M^*=\Omega ^*/\Gamma$
is compact and strictly convex, and the dual action of
$M^*=\Omega ^*/\Gamma$
is compact and strictly convex, and the dual action of
![]() $\Gamma$
preserves
$\Gamma$
preserves
![]() $U^0$
, which contradicts (1.14). Thus
$U^0$
, which contradicts (1.14). Thus
![]() $Y\ne \emptyset$
, so
$Y\ne \emptyset$
, so
![]() $Y\subset \textrm {Fr}\Omega$
. Since
$Y\subset \textrm {Fr}\Omega$
. Since
![]() $M$
is strictly convex,
$M$
is strictly convex,
![]() $Y=c$
is a single point that is fixed by
$Y=c$
is a single point that is fixed by
![]() $\Gamma$
.
$\Gamma$
.
Thus every non-trivial element of
![]() $\Gamma$
has an axis with one endpoint at
$\Gamma$
has an axis with one endpoint at
![]() $c$
. If
$c$
. If
![]() $\ell$
and
$\ell$
and
![]() $\ell ^{\prime}$
are the axes of
$\ell ^{\prime}$
are the axes of
![]() $\gamma ,\gamma ^{\prime}\in \Gamma$
, then they limit on
$\gamma ,\gamma ^{\prime}\in \Gamma$
, then they limit on
![]() $c$
. Now
$c$
. Now
![]() $\Omega$
is
$\Omega$
is
![]() $C^1$
at
$C^1$
at
![]() $c$
by (2.5) so
$c$
by (2.5) so
![]() $d_{\Omega }(p,\ell ^{\prime})\to 0$
as the point
$d_{\Omega }(p,\ell ^{\prime})\to 0$
as the point
![]() $p$
on
$p$
on
![]() $\ell$
approaches
$\ell$
approaches
![]() $c$
. Let
$c$
. Let
![]() $\pi :\Omega \to M$
be the projection. Then
$\pi :\Omega \to M$
be the projection. Then
![]() $C=\pi (\ell )$
and
$C=\pi (\ell )$
and
![]() $C^{\prime}=\pi (\ell ^{\prime})$
are closed geodesics in
$C^{\prime}=\pi (\ell ^{\prime})$
are closed geodesics in
![]() $M$
that become arbitrarily close to each other. It follows that
$M$
that become arbitrarily close to each other. It follows that
![]() $C=C^{\prime}$
, so
$C=C^{\prime}$
, so
![]() $\ell =\ell ^{\prime}$
. Thus
$\ell =\ell ^{\prime}$
. Thus
![]() $\Gamma$
preserves
$\Gamma$
preserves
![]() $\ell$
which contradicts (1.14) unless
$\ell$
which contradicts (1.14) unless
![]() $\Omega =\ell$
, but then
$\Omega =\ell$
, but then
![]() $\dim M=1$
.
$\dim M=1$
.
The following is a special case of Chuckrow’s theorem (see [Reference ChuckrowChu67] or [Reference KapovichKap09](8.4)).
Lemma 4.2.
If
![]() $M$
is a closed, strictly convex, projective manifold and
$M$
is a closed, strictly convex, projective manifold and
![]() $\dim M\geqslant 2$
, then the closure of
$\dim M\geqslant 2$
, then the closure of
![]() $\textrm {Rep}_S(M)$
in
$\textrm {Rep}_S(M)$
in
![]() $\textrm {Rep}(M)$
consists of discrete and faithful representations.
$\textrm {Rep}(M)$
consists of discrete and faithful representations.
Proof.
Let
![]() $d$
be the metric on
$d$
be the metric on
![]() $G=\textrm {GL}(m+1,{\mathbb{R}})$
given by
$G=\textrm {GL}(m+1,{\mathbb{R}})$
given by
![]() $d(g,h)=\max |(g-h)_{ij}|$
and set
$d(g,h)=\max |(g-h)_{ij}|$
and set
![]() $\|g\|=d(I,g)$
. Let
$\|g\|=d(I,g)$
. Let
![]() $\mathcal{W}\subset \pi _1M$
be a finite generating set. Suppose the sequence
$\mathcal{W}\subset \pi _1M$
be a finite generating set. Suppose the sequence
![]() $\rho _n\in \textrm {Rep}_S(M)$
converges to
$\rho _n\in \textrm {Rep}_S(M)$
converges to
![]() $\rho _{\infty }\in \textrm {Rep}(M)$
. Then there is a compact set
$\rho _{\infty }\in \textrm {Rep}(M)$
. Then there is a compact set
![]() $K\subset G$
such that
$K\subset G$
such that
![]() $\rho _n(\mathcal{W})\subset K$
for all
$\rho _n(\mathcal{W})\subset K$
for all
![]() $n$
.
$n$
.
The map
![]() $\theta :G\times G\to G$
given by
$\theta :G\times G\to G$
given by
![]() $\theta (g,h)=[[g,h],h]$
has zero derivative on
$\theta (g,h)=[[g,h],h]$
has zero derivative on
![]() $G\times {\textrm {I}}$
. Thus there is a neighborhood
$G\times {\textrm {I}}$
. Thus there is a neighborhood
![]() $U\subset G$
of the identity such that if
$U\subset G$
of the identity such that if
![]() $k\in K$
and
$k\in K$
and
![]() $u\in U$
, then
$u\in U$
, then
![]() $\|\; [[k,u],u]\;\|\leqslant \|\;u\;\|/2$
.
$\|\; [[k,u],u]\;\|\leqslant \|\;u\;\|/2$
.
Since
![]() $\rho =\rho _n$
is discrete, there is
$\rho =\rho _n$
is discrete, there is
![]() $1\ne \alpha \in \pi _1M$
that minimizes
$1\ne \alpha \in \pi _1M$
that minimizes
![]() $\|\rho (\alpha )\|$
. Suppose that
$\|\rho (\alpha )\|$
. Suppose that
![]() $\rho (\alpha )\in U$
. If
$\rho (\alpha )\in U$
. If
![]() $\beta \in \mathcal{W}$
, then
$\beta \in \mathcal{W}$
, then
![]() $\rho (\beta )\in K$
, so
$\rho (\beta )\in K$
, so
![]() $\|\;\rho [[\beta ,\alpha ],\alpha ]\;\|\leqslant \|\;\rho \alpha \;\|/2$
. By minimality,
$\|\;\rho [[\beta ,\alpha ],\alpha ]\;\|\leqslant \|\;\rho \alpha \;\|/2$
. By minimality,
![]() $\rho [[\beta ,\alpha ],\alpha ]={\textrm {I}}$
, and since
$\rho [[\beta ,\alpha ],\alpha ]={\textrm {I}}$
, and since
![]() $\rho$
is injective,
$\rho$
is injective,
![]() $[[\beta ,\alpha ],\alpha ]={\textrm {I}}$
. By (1.13)
$[[\beta ,\alpha ],\alpha ]={\textrm {I}}$
. By (1.13)
![]() $\alpha$
and
$\alpha$
and
![]() $\beta$
commute. Since
$\beta$
commute. Since
![]() $\mathcal{W}$
is a generating set,
$\mathcal{W}$
is a generating set,
![]() $\alpha$
is central in
$\alpha$
is central in
![]() $\pi _1M$
. Thus the entire group preserves the axis of
$\pi _1M$
. Thus the entire group preserves the axis of
![]() $\alpha$
. This contradicts (1.14) because
$\alpha$
. This contradicts (1.14) because
![]() $\dim M \geqslant 2$
. Thus
$\dim M \geqslant 2$
. Thus
![]() $\rho (\alpha )\notin U.$
Since
$\rho (\alpha )\notin U.$
Since
![]() $U$
is an open neighborhood of the identity, it contains an open metric ball
$U$
is an open neighborhood of the identity, it contains an open metric ball
![]() $U^{\prime}$
, and since
$U^{\prime}$
, and since
![]() $\rho (\alpha )$
is of minimal norm, we have
$\rho (\alpha )$
is of minimal norm, we have
![]() $\rho (\gamma )\notin U^{\prime}$
for all
$\rho (\gamma )\notin U^{\prime}$
for all
![]() $1\neq \gamma \in \pi _1M.$
This implies that
$1\neq \gamma \in \pi _1M.$
This implies that
![]() $\rho _{\infty }$
is discrete and faithful.
$\rho _{\infty }$
is discrete and faithful.
Let
![]() $\mathfrak{B}=\prod _{i=1}^n[-1,1]\subset {\mathbb{R}}^n\subset \mathbb{RP}^n$
. For each
$\mathfrak{B}=\prod _{i=1}^n[-1,1]\subset {\mathbb{R}}^n\subset \mathbb{RP}^n$
. For each
![]() $K\gt 0$
, the set
$K\gt 0$
, the set
![]() $K\cdot \mathfrak{B}=\prod _{i=1}^n[-K,K]$
is called a box.
$K\cdot \mathfrak{B}=\prod _{i=1}^n[-K,K]$
is called a box.
Lemma 4.3 (Box estimate). If
![]() $A=(A_{ij})\in \textrm {GL}(n+1,{\mathbb R})$
and
$A=(A_{ij})\in \textrm {GL}(n+1,{\mathbb R})$
and
![]() $K\geqslant 1$
and
$K\geqslant 1$
and
![]() $[A](\mathfrak{B})\subset K.\mathfrak{B}$
, then
$[A](\mathfrak{B})\subset K.\mathfrak{B}$
, then
Proof.
Set
![]() $\alpha =A_{n+1,n+1}$
. Using the standard basis we have
$\alpha =A_{n+1,n+1}$
. Using the standard basis we have
First consider the entries
![]() $A_{i,n+1}$
in the last column of
$A_{i,n+1}$
in the last column of
![]() $A$
. Since
$A$
. Since
![]() $[e_{n+1}]=0\in \mathfrak{B}$
we have
$[e_{n+1}]=0\in \mathfrak{B}$
we have
It follows that
![]() $|A_{i,n+1}/\alpha |\leqslant K$
. This establishes the bound when
$|A_{i,n+1}/\alpha |\leqslant K$
. This establishes the bound when
![]() $j=n+1$
and
$j=n+1$
and
![]() $i\leqslant n$
.
$i\leqslant n$
.
Next consider the entries
![]() $A_{n+1,j}$
in the bottom row with
$A_{n+1,j}$
in the bottom row with
![]() $j\leqslant n$
. Observe that
$j\leqslant n$
. Observe that
Then
![]() $[A]p=[A(te_j+e_{n+1})]\in K\cdot \mathfrak{B}$
. This is in
$[A]p=[A(te_j+e_{n+1})]\in K\cdot \mathfrak{B}$
. This is in
![]() ${\mathbb R}^n$
so the
${\mathbb R}^n$
so the
![]() $e_{n+1}$
component is not zero. Hence,
$e_{n+1}$
component is not zero. Hence,
![]() $t A_{n+1,j}+\alpha \ne 0$
whenever
$t A_{n+1,j}+\alpha \ne 0$
whenever
![]() $|\;t\;|\leqslant 1$
and it follows that
$|\;t\;|\leqslant 1$
and it follows that
![]() $|A_{n+1,j}| \lt |\alpha |$
. Since
$|A_{n+1,j}| \lt |\alpha |$
. Since
![]() $K\geqslant 1$
the required bound follows when
$K\geqslant 1$
the required bound follows when
![]() $i=n+1$
and
$i=n+1$
and
![]() $j\leqslant n$
.
$j\leqslant n$
.
The remaining entries are
![]() $1\leqslant i,j\leqslant n$
. Since
$1\leqslant i,j\leqslant n$
. Since
![]() $p=[p_1:\cdots :p_{n+1}]=[A(te_j+e_{n+1})]\in K\cdot \mathfrak{B}$
it follows that
$p=[p_1:\cdots :p_{n+1}]=[A(te_j+e_{n+1})]\in K\cdot \mathfrak{B}$
it follows that
For all
![]() $|t|\leqslant 1$
the denominator is not zero hence
$|t|\leqslant 1$
the denominator is not zero hence
![]() $|A_{n+1,j}|\lt |\alpha |$
. It follows that
$|A_{n+1,j}|\lt |\alpha |$
. It follows that
Thus
We may choose the sign of
![]() $t=\pm 1$
so that
$t=\pm 1$
so that
![]() $A_{i,n+1}$
and
$A_{i,n+1}$
and
![]() $t A_{i,j}$
have the same sign. Then
$t A_{i,j}$
have the same sign. Then
This gives the result
![]() $ \left | A_{i,j}\right |\leqslant 2|\alpha |\cdot K$
in this remaining case.
$ \left | A_{i,j}\right |\leqslant 2|\alpha |\cdot K$
in this remaining case.
If
![]() $\Omega \subset {\mathbb{R}}^n$
has finite positive Lebesgue measure and the centroid of
$\Omega \subset {\mathbb{R}}^n$
has finite positive Lebesgue measure and the centroid of
![]() $\Omega$
is
$\Omega$
is
![]() $\mu (\Omega )=0$
, then
$\mu (\Omega )=0$
, then
is a positive-–definite quadratic form on
![]() ${\mathbb{R}}^n$
called the inertia tensor.
${\mathbb{R}}^n$
called the inertia tensor.
Lemma 4.4 (Uniform estimate). For each dimension
![]() $n$
there is
$n$
there is
![]() $K=K(n)\gt 1$
such that if
$K=K(n)\gt 1$
such that if
![]() $\Omega \subset {\mathbb R}^n$
is an open bounded convex set with inertia tensor
$\Omega \subset {\mathbb R}^n$
is an open bounded convex set with inertia tensor
![]() $Q_{_{\Omega }}=x_1^2+\cdots +x_n^2$
and centroid at the origin, then
$Q_{_{\Omega }}=x_1^2+\cdots +x_n^2$
and centroid at the origin, then
![]() $K^{-1}\mathfrak{B}\subset \Omega \subset K\cdot \mathfrak{B}$
. Moreover, if
$K^{-1}\mathfrak{B}\subset \Omega \subset K\cdot \mathfrak{B}$
. Moreover, if
![]() $A\in \textrm {GL}(\Omega )$
, then
$A\in \textrm {GL}(\Omega )$
, then
![]() $|A_{ij}|\leqslant K\cdot |A_{n+1,n+1}|$
.
$|A_{ij}|\leqslant K\cdot |A_{n+1,n+1}|$
.
Proof.
The first conclusion follows from the theorem of Fritz John [Reference JohnJoh48], see also [Reference BallBal92]. Let
![]() $D\in \textrm {GL}(n+1,{\mathbb{R}})$
be the diagonal matrix
$D\in \textrm {GL}(n+1,{\mathbb{R}})$
be the diagonal matrix
![]() $\textrm {Diag}(K,\cdots ,K,1)$
, then
$\textrm {Diag}(K,\cdots ,K,1)$
, then
![]() $\mathfrak{B}\subset D(\Omega )\subset K^2\mathfrak{B}$
. Set
$\mathfrak{B}\subset D(\Omega )\subset K^2\mathfrak{B}$
. Set
![]() $A^{\prime}=D\cdot A\cdot D^{-1}$
, then
$A^{\prime}=D\cdot A\cdot D^{-1}$
, then
![]() $A^{\prime}\in \textrm {GL}(D(\Omega ))$
, thus
$A^{\prime}\in \textrm {GL}(D(\Omega ))$
, thus
![]() $|A^{\prime}_{ij}|\leqslant 2K\cdot |A^{\prime}_{n+1,n+1}|$
by (4.3). Now
$|A^{\prime}_{ij}|\leqslant 2K\cdot |A^{\prime}_{n+1,n+1}|$
by (4.3). Now
![]() $|A^{\prime}_{n+1,n+1}|=|A_{n+1,n+1}|$
and
$|A^{\prime}_{n+1,n+1}|=|A_{n+1,n+1}|$
and
![]() $|A_{i,j}|\leqslant K |A^{\prime}_{i,j}|$
thus
$|A_{i,j}|\leqslant K |A^{\prime}_{i,j}|$
thus
![]() $|A_{ij}|\leqslant 2K^3\cdot |A_{n+1,n+1}|$
. The result now holds using the constant
$|A_{ij}|\leqslant 2K^3\cdot |A_{n+1,n+1}|$
. The result now holds using the constant
![]() $2K^3$
.
$2K^3$
.
Proof of Closed Theorem 2. Suppose
![]() $\rho \in \textrm {Rep}(M)$
is the limit of the sequence
$\rho \in \textrm {Rep}(M)$
is the limit of the sequence
![]() $\rho _k\in \textrm {Rep}_s(M)$
. Let
$\rho _k\in \textrm {Rep}_s(M)$
. Let
![]() $\Omega _k\subset \mathbb{RP}^n$
be the properly convex open set preserved by
$\Omega _k\subset \mathbb{RP}^n$
be the properly convex open set preserved by
![]() $\Gamma _k=\rho _k(\pi _1M)$
, then
$\Gamma _k=\rho _k(\pi _1M)$
, then
![]() $M\cong M_k=\Omega _k/\Gamma _k$
. Choose an affine patch
$M\cong M_k=\Omega _k/\Gamma _k$
. Choose an affine patch
![]() ${\mathbb R}^n\subset {\mathbb R}P^n$
. Then by (2.8) there is
${\mathbb R}^n\subset {\mathbb R}P^n$
. Then by (2.8) there is
![]() $\alpha _k\in \textrm {PO}(n+1)$
such that
$\alpha _k\in \textrm {PO}(n+1)$
such that
![]() $\alpha _k(\Omega _k)\subset {\mathbb R}^n$
and has center
$\alpha _k(\Omega _k)\subset {\mathbb R}^n$
and has center
![]() $0\in {\mathbb R}^n$
. We may choose
$0\in {\mathbb R}^n$
. We may choose
![]() $\alpha _k$
so that the interia tensor
$\alpha _k$
so that the interia tensor
![]() $Q_k=Q_{\alpha _k(\Omega _k)}$
is diagonal in the standard coordinates on
$Q_k=Q_{\alpha _k(\Omega _k)}$
is diagonal in the standard coordinates on
![]() ${\mathbb R}^n$
, and the entries on the main diagonal of
${\mathbb R}^n$
, and the entries on the main diagonal of
![]() $Q_k$
are non-increasing going down the diagonal. Since
$Q_k$
are non-increasing going down the diagonal. Since
![]() $\textrm {PO}(n+1)$
is compact, after subsequencing we may assume the conjugates of
$\textrm {PO}(n+1)$
is compact, after subsequencing we may assume the conjugates of
![]() $\rho _k$
by
$\rho _k$
by
![]() $\alpha _k$
converge. We now replace the original sequence of representations and domains by this new sequence.
$\alpha _k$
converge. We now replace the original sequence of representations and domains by this new sequence.
Let
![]() $K=K(n)$
be given by (4.4). There is a unique positive diagonal matrix
$K=K(n)$
be given by (4.4). There is a unique positive diagonal matrix
![]() $D_k$
such that
$D_k$
such that
![]() $Q_k=D_k^{-2}$
. Set
$Q_k=D_k^{-2}$
. Set
![]() $\Omega ^{\prime}_k=D_k\Omega _k$
, then
$\Omega ^{\prime}_k=D_k\Omega _k$
, then
![]() $Q_{\Omega ^{\prime}_k}=x_1^2+\cdots +x_n^2$
. By (4.4), there is
$Q_{\Omega ^{\prime}_k}=x_1^2+\cdots +x_n^2$
. By (4.4), there is
![]() $K\gt 1$
depending only on
$K\gt 1$
depending only on
![]() $n$
, such that
$n$
, such that
Given
![]() $g\in \pi _1M$
, then
$g\in \pi _1M$
, then
![]() $A=A(k,g)=\rho _k(g)\in \textrm {SL}(n+1,{\mathbb R})$
preserves
$A=A(k,g)=\rho _k(g)\in \textrm {SL}(n+1,{\mathbb R})$
preserves
![]() $\Omega _k$
. The matrix
$\Omega _k$
. The matrix
preserves
![]() $\Omega ^{\prime}_k$
. By (4.4)
$\Omega ^{\prime}_k$
. By (4.4)
Since
![]() $D_k$
is diagonal it follows that
$D_k$
is diagonal it follows that
Now
![]() $A_{n+1,n+1}=A(k,g)_{n+1,n+1}$
converges as
$A_{n+1,n+1}=A(k,g)_{n+1,n+1}$
converges as
![]() $k\to \infty$
for each
$k\to \infty$
for each
![]() $g$
. Hence the entries of
$g$
. Hence the entries of
![]() $B(k,g)$
are uniformly bounded for fixed
$B(k,g)$
are uniformly bounded for fixed
![]() $g$
as
$g$
as
![]() $k\to \infty$
. Thus we may pass to a subsequence where
$k\to \infty$
. Thus we may pass to a subsequence where
![]() $B(k,g)=D_k\rho _k(g)D_k^{-1}$
converges for every
$B(k,g)=D_k\rho _k(g)D_k^{-1}$
converges for every
![]() $g\in \pi _1M$
, and this gives a limiting representation
$g\in \pi _1M$
, and this gives a limiting representation
![]() $\sigma =\lim D_k\rho _kD_k^{-1}$
.
$\sigma =\lim D_k\rho _kD_k^{-1}$
.
The space consisting of properly convex open sets
![]() $\Omega$
with
$\Omega$
with
![]() $K^{-1}\cdot \mathcal{B}_1\subset \Omega \subset K\cdot \mathcal{B}_1$
is compact. Therefore there is a subsequence so that
$K^{-1}\cdot \mathcal{B}_1\subset \Omega \subset K\cdot \mathcal{B}_1$
is compact. Therefore there is a subsequence so that
![]() $\Omega =\lim \Omega _k^{\prime}$
exists. Then
$\Omega =\lim \Omega _k^{\prime}$
exists. Then
![]() $K^{-1}\cdot \mathfrak{B}_1\subset \Omega \subset K\cdot \mathfrak{B}_1$
, hence
$K^{-1}\cdot \mathfrak{B}_1\subset \Omega \subset K\cdot \mathfrak{B}_1$
, hence
![]() $\Omega$
is open and properly convex. Then
$\Omega$
is open and properly convex. Then
![]() $\sigma$
is discrete and faithful by (4.2), and
$\sigma$
is discrete and faithful by (4.2), and
![]() $\Gamma =\sigma (\pi _1M)$
preserves
$\Gamma =\sigma (\pi _1M)$
preserves
![]() $\Omega$
, so
$\Omega$
, so
![]() $N=\Omega /\Gamma$
is a properly convex manifold. Since
$N=\Omega /\Gamma$
is a properly convex manifold. Since
![]() $M$
is closed and
$M$
is closed and
![]() $\pi _1M\cong \pi _1N$
, then by (1.10)
$\pi _1M\cong \pi _1N$
, then by (1.10)
![]() $N$
is also closed. Since
$N$
is also closed. Since
![]() $M$
is strictly convex, (1.11) implies
$M$
is strictly convex, (1.11) implies
![]() $N$
is strictly convex.
$N$
is strictly convex.
Since
![]() $\textrm {Rep}_P(N)$
is open, for
$\textrm {Rep}_P(N)$
is open, for
![]() $D_k\rho _kD_k^{-1}$
close enough to
$D_k\rho _kD_k^{-1}$
close enough to
![]() $\sigma$
, there is a properly convex open set
$\sigma$
, there is a properly convex open set
![]() $\Omega ^{\prime\prime}_k\subset \mathbb{RP}^n$
that is preserved by
$\Omega ^{\prime\prime}_k\subset \mathbb{RP}^n$
that is preserved by
![]() $\Gamma _k$
and
$\Gamma _k$
and
![]() $N_k=\Omega ^{\prime\prime}_k/\Gamma _k$
is homeomorphic to
$N_k=\Omega ^{\prime\prime}_k/\Gamma _k$
is homeomorphic to
![]() $N$
. By (1.11)
$N$
. By (1.11)
![]() $N_k$
is strictly convex. By (1.15)
$N_k$
is strictly convex. By (1.15)
![]() $\Omega ^{\prime\prime}_k=\Omega _k$
so
$\Omega ^{\prime\prime}_k=\Omega _k$
so
![]() $N\cong N_k=M_k\cong M$
. Thus
$N\cong N_k=M_k\cong M$
. Thus
![]() $\sigma \in \textrm {Rep}_S(M)$
.
$\sigma \in \textrm {Rep}_S(M)$
.
If
![]() $D_k$
does not remain bounded, since the entries are non-increasing going down the diagonal, and
$D_k$
does not remain bounded, since the entries are non-increasing going down the diagonal, and
![]() $\rho _k(g)$
remains bounded,
$\rho _k(g)$
remains bounded,
![]() $\sigma (g)$
is block upper triangular and therefore
$\sigma (g)$
is block upper triangular and therefore
![]() $\sigma$
is reducible. Since
$\sigma$
is reducible. Since
![]() $N$
is strictly convex, (4.1) implies
$N$
is strictly convex, (4.1) implies
![]() $\sigma$
is irreducible, therefore
$\sigma$
is irreducible, therefore
![]() $D_k$
stays bounded. Hence we may subsequence the
$D_k$
stays bounded. Hence we may subsequence the
![]() $D_k$
so they converge to
$D_k$
so they converge to
![]() $D$
. Then
$D$
. Then
![]() $\rho =D^{-1}\sigma D$
, so
$\rho =D^{-1}\sigma D$
, so
![]() $\rho \in \textrm {Rep}_S(M)$
.
$\rho \in \textrm {Rep}_S(M)$
.
Acknowledgements
The first author thanks the Sydney Mathematical Research Institute (SMRI) for partial support and hospitality while writing this paper. He also thanks the audience at SMRI that participated in a presentation of this material. We thank the referee for a splendid job and a shorter proof of (1.13).
Funding statement
Research of the second author is supported in part under the Australian Research Council’s ARC Future Fellowship FT170100316.
Conflicts of interest
None.
Journal information
Moduli is published as a joint venture of the Foundation Compositio Mathematica and the London Mathematical Society. As not-for-profit organisations, the Foundation and Society reinvest
![]() $100\%$
of any surplus generated from their publications back into mathematics through their charitable activities.
$100\%$
of any surplus generated from their publications back into mathematics through their charitable activities.