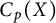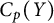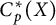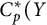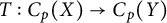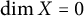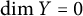1 Introduction
All spaces in this article, if not said otherwise, are Tychonoff spaces and all maps are continuous. By
![]() $C(X)$
(resp.,
$C(X)$
(resp.,
![]() $C^*(X)$
), we denote the set of all continuous (resp., continuous and bounded) real-valued functions on a space X. We write
$C^*(X)$
), we denote the set of all continuous (resp., continuous and bounded) real-valued functions on a space X. We write
![]() $C_p(X)$
(resp.,
$C_p(X)$
(resp.,
![]() $C_p^*(X)$
) for the spaces
$C_p^*(X)$
) for the spaces
![]() $C(X)$
(resp.,
$C(X)$
(resp.,
![]() $C^*(X)$
) endowed with the pointwise topology. More information about the spaces
$C^*(X)$
) endowed with the pointwise topology. More information about the spaces
![]() $C_p(X)$
can be found in [Reference Tkachuk20]. By dimension, we mean the covering dimension
$C_p(X)$
can be found in [Reference Tkachuk20]. By dimension, we mean the covering dimension
![]() $\dim $
defined by finite functionally open covers (see [Reference Engelking2]). According to that definition, we have
$\dim $
defined by finite functionally open covers (see [Reference Engelking2]). According to that definition, we have
![]() $\dim X=\dim \beta X$
, where
$\dim X=\dim \beta X$
, where
![]() $\beta X$
is the Čech–Stone compactification of X.
$\beta X$
is the Čech–Stone compactification of X.
After the striking result of Pestov [Reference Pestov18] that
![]() $\dim X=\dim Y$
provided that
$\dim X=\dim Y$
provided that
![]() $C_p(X)$
and
$C_p(X)$
and
![]() $C_p(Y)$
are linearly homeomorphic, and Gul’ko’s [Reference Gul’ko7] generalization of Pestov’s theorem that the same is true for uniformly continuous homeomorphisms, a question arose whether
$C_p(Y)$
are linearly homeomorphic, and Gul’ko’s [Reference Gul’ko7] generalization of Pestov’s theorem that the same is true for uniformly continuous homeomorphisms, a question arose whether
![]() $\dim Y\leq \dim X$
if there is continuous linear surjection from
$\dim Y\leq \dim X$
if there is continuous linear surjection from
![]() $C_p(X)$
onto
$C_p(X)$
onto
![]() $C_p(Y)$
(see [Reference Arkhangel’skii, van Mill and Reed1]). This was answered negatively by Leiderman–Levin–Pestov [Reference Leiderman, Levin and Pestov14] and Leiderman–Morris–Pestov [Reference Leiderman, Morris and Pestov15]. On the other hand, it was shown in [Reference Leiderman, Levin and Pestov14] that if there is a linear continuous surjection
$C_p(Y)$
(see [Reference Arkhangel’skii, van Mill and Reed1]). This was answered negatively by Leiderman–Levin–Pestov [Reference Leiderman, Levin and Pestov14] and Leiderman–Morris–Pestov [Reference Leiderman, Morris and Pestov15]. On the other hand, it was shown in [Reference Leiderman, Levin and Pestov14] that if there is a linear continuous surjection
![]() $C_p(X)\to C_p(Y)$
such that X and Y are compact metrizable spaces and
$C_p(X)\to C_p(Y)$
such that X and Y are compact metrizable spaces and
![]() $\dim X=0$
, then
$\dim X=0$
, then
![]() $\dim Y=0$
. The last result was extended for arbitrary compact spaces by Kawamura–Leiderman [Reference Kawamura and Leiderman10] who also raised the question whether this is true for any Tychonoff spaces X and Y. In this article, we provide a positive answer to that question and discuss the situation when the surjection
$\dim Y=0$
. The last result was extended for arbitrary compact spaces by Kawamura–Leiderman [Reference Kawamura and Leiderman10] who also raised the question whether this is true for any Tychonoff spaces X and Y. In this article, we provide a positive answer to that question and discuss the situation when the surjection
![]() $T:C_p(X)\to C_p(Y)$
is uniformly continuous. Let us note that the preservation of dimension under linear homeomorphisms doesn’t hold for function spaces with the uniform norm topology. Indeed, according to the classical result of Milutin [Reference Milutin17] if X and Y are any uncountable metrizable compacta, then there is a linear homeomorphism between the Banach spaces
$T:C_p(X)\to C_p(Y)$
is uniformly continuous. Let us note that the preservation of dimension under linear homeomorphisms doesn’t hold for function spaces with the uniform norm topology. Indeed, according to the classical result of Milutin [Reference Milutin17] if X and Y are any uncountable metrizable compacta, then there is a linear homeomorphism between the Banach spaces
![]() $C(X)$
and
$C(X)$
and
![]() $C(Y)$
.
$C(Y)$
.
Suppose
![]() $E_p(X)\subset C_p(X)$
and
$E_p(X)\subset C_p(X)$
and
![]() $E_p(Y)\subset C_p(Y)$
are subspaces containing the zero functions on X and Y, respectively. Recall that a map
$E_p(Y)\subset C_p(Y)$
are subspaces containing the zero functions on X and Y, respectively. Recall that a map
![]() $\varphi : E_p(X)\to E_p(Y)$
is uniformly continuous, if for every neighborhood U of the zero function in
$\varphi : E_p(X)\to E_p(Y)$
is uniformly continuous, if for every neighborhood U of the zero function in
![]() $E_p(Y),$
there is a neighborhood V of the zero function in
$E_p(Y),$
there is a neighborhood V of the zero function in
![]() $E_p(X)$
such that
$E_p(X)$
such that
![]() $f,g\in E_p(X)$
and
$f,g\in E_p(X)$
and
![]() $f-g\in V$
implies
$f-g\in V$
implies
![]() $\varphi (f)-\varphi (g)\in U$
. Evidently, if
$\varphi (f)-\varphi (g)\in U$
. Evidently, if
![]() $E_p(X)$
and
$E_p(X)$
and
![]() $E_p(Y)$
are linear spaces, then every linear continuous map between
$E_p(Y)$
are linear spaces, then every linear continuous map between
![]() $E_p(X)$
and
$E_p(X)$
and
![]() $E_p(Y)$
is uniformly continuous. If
$E_p(Y)$
is uniformly continuous. If
![]() ${f\in C_p(X)}$
is a bounded function, then
${f\in C_p(X)}$
is a bounded function, then
![]() $||f||$
stands for the supremum norm of f. The notion of c-good maps was introduced in [Reference Gorak, Krupski and Marciszewski6] (see also [Reference Gartside and Feng5]), where c is a positive number. A map
$||f||$
stands for the supremum norm of f. The notion of c-good maps was introduced in [Reference Gorak, Krupski and Marciszewski6] (see also [Reference Gartside and Feng5]), where c is a positive number. A map
![]() $\varphi : E_p(X)\to E_p(Y)$
is c-good if for every bounded function
$\varphi : E_p(X)\to E_p(Y)$
is c-good if for every bounded function
![]() $g\in E_p(Y)$
there exists a bounded function
$g\in E_p(Y)$
there exists a bounded function
![]() $f\in E_p(X)$
such that
$f\in E_p(X)$
such that
![]() $\varphi (f)=g$
and
$\varphi (f)=g$
and
![]() $||f||\leq c||g||$
.
$||f||\leq c||g||$
.
Everywhere below, by
![]() $D(X),$
we denote either
$D(X),$
we denote either
![]() $C^*(X)$
or
$C^*(X)$
or
![]() $C(X)$
. Here is one of our main results.
$C(X)$
. Here is one of our main results.
Theorem 1.1 Let
![]() $T:D_p(X)\to D_p(Y)$
be a c-good uniformly continuous surjection for some
$T:D_p(X)\to D_p(Y)$
be a c-good uniformly continuous surjection for some
![]() $c>0$
. Then ,Y is zero-dimensional provided so is X.
$c>0$
. Then ,Y is zero-dimensional provided so is X.
Corollary 1.2 Suppose there is a linear continuous surjection from
![]() $C_p^*(X)$
onto
$C_p^*(X)$
onto
![]() $C_p^*(Y)$
. Then, Y is zero-dimensional provided that so is X.
$C_p^*(Y)$
. Then, Y is zero-dimensional provided that so is X.
Corollary 1.2 follows from Theorem 1.1 because every linear continuous surjection between
![]() $C_p^*(X)$
and
$C_p^*(X)$
and
![]() $C_p^*(Y)$
is c-good for some
$C_p^*(Y)$
is c-good for some
![]() $c>0$
(see Proposition 3.3). Moreover, as one of the referees observed, it is not always possible to have a continuous linear surjection
$c>0$
(see Proposition 3.3). Moreover, as one of the referees observed, it is not always possible to have a continuous linear surjection
![]() $T:C_p^*(X)\to C_p(Y)$
with
$T:C_p^*(X)\to C_p(Y)$
with
![]() $C_p(Y)\neq C_p^*(Y)$
. Indeed, we consider the composition
$C_p(Y)\neq C_p^*(Y)$
. Indeed, we consider the composition
![]() $T\circ i$
, where
$T\circ i$
, where
![]() $i:C_p(\beta X)\to C_p^*(X)$
is the restriction map. Then, according to [Reference Uspenskii21, Proposition 2], Y is pseudocompact and
$i:C_p(\beta X)\to C_p^*(X)$
is the restriction map. Then, according to [Reference Uspenskii21, Proposition 2], Y is pseudocompact and
![]() $C_p(Y)=C_p^*(Y)$
.
$C_p(Y)=C_p^*(Y)$
.
We consider properties
![]() $\mathcal P$
of
$\mathcal P$
of
![]() $\sigma $
-compact metrizable spaces such that:
$\sigma $
-compact metrizable spaces such that:
-
(a) if
 $X\in \mathcal P$
and
$X\in \mathcal P$
and
 $F\subset X$
is closed, then
$F\subset X$
is closed, then
 $F\in \mathcal P$
;
$F\in \mathcal P$
; -
(b) if X is a countable union of closed subsets each having the property
 $\mathcal P$
, then
$\mathcal P$
, then
 $X\in \mathcal P$
;
$X\in \mathcal P$
; -
(c) if
 $f:X\to Y$
is a perfect map with countable fibers and
$f:X\to Y$
is a perfect map with countable fibers and
 $Y\in \mathcal P$
, then
$Y\in \mathcal P$
, then
 $X\in \mathcal P$
.
$X\in \mathcal P$
.
For example, zero-dimensionality, strongly countable-dimensionality, and C-space property are finitely multiplicative properties satisfying conditions (a)–(c). Another two properties of this type, but not finitely multiplicative, are weakly infinite-dimensionality, or
![]() $(m-C)$
-spaces in the sense of Fedorchuk [Reference Fedorchuk4]. The definition of all dimension-like properties mentioned above, and explanations that they satisfy conditions (a)–(c) can be found at the end of Section 2.
$(m-C)$
-spaces in the sense of Fedorchuk [Reference Fedorchuk4]. The definition of all dimension-like properties mentioned above, and explanations that they satisfy conditions (a)–(c) can be found at the end of Section 2.
For
![]() $\sigma $
-compact metrizable spaces, we have the following version of Theorem 1.1 (actually Theorem 1.3 below is true for any topological property
$\sigma $
-compact metrizable spaces, we have the following version of Theorem 1.1 (actually Theorem 1.3 below is true for any topological property
![]() $\mathcal P$
satisfying conditions (a)–(c)).
$\mathcal P$
satisfying conditions (a)–(c)).
Theorem 1.3 Suppose X and Y are
![]() $\sigma $
-compact metrizable spaces and let
$\sigma $
-compact metrizable spaces and let
![]() $T:D_p(X)\to D_p(Y)$
be a c-good uniformly continuous surjection for some
$T:D_p(X)\to D_p(Y)$
be a c-good uniformly continuous surjection for some
![]() $c>0$
. If all finite powers of X are weakly infinite-dimensional or
$c>0$
. If all finite powers of X are weakly infinite-dimensional or
![]() $(m-C)$
-spaces, then all finite powers of Y are also weakly infinite-dimensional or
$(m-C)$
-spaces, then all finite powers of Y are also weakly infinite-dimensional or
![]() $(m-C)$
-spaces.
$(m-C)$
-spaces.
Krupski [Reference Krupski11] proved similar result for
![]() $\sigma $
-compact metrizable spaces: if
$\sigma $
-compact metrizable spaces: if
![]() $T:C_p(X)\to C_p(Y)$
is a continuous open surjection and all powers of X are weakly infinite-dimensional or
$T:C_p(X)\to C_p(Y)$
is a continuous open surjection and all powers of X are weakly infinite-dimensional or
![]() $(m-C)$
-spaces, then Y is also weakly infinite-dimensional of has the property
$(m-C)$
-spaces, then Y is also weakly infinite-dimensional of has the property
![]() $m-C$
. Theorem 1.3 was established in [Reference Gorak, Krupski and Marciszewski6] in the special case when
$m-C$
. Theorem 1.3 was established in [Reference Gorak, Krupski and Marciszewski6] in the special case when
![]() $X,Y$
are compact metrizable spaces and the property is either zero-dimensionality or strong countable-dimensionality.
$X,Y$
are compact metrizable spaces and the property is either zero-dimensionality or strong countable-dimensionality.
The notion of c-good maps is crucial in the proof of the above results. One of the referees observed that if
![]() $X=Y$
is the space of natural numbers, then the continuous linear surjection
$X=Y$
is the space of natural numbers, then the continuous linear surjection
![]() $T:C_p(X)\to C_p(Y)$
,
$T:C_p(X)\to C_p(Y)$
,
![]() $T(f)(n)=\frac {1}{n+1}f(n)$
, is not c-good for any c. Therefore, as the referee suggested, the more interesting question is whether the existence of a linear continuous surjection
$T(f)(n)=\frac {1}{n+1}f(n)$
, is not c-good for any c. Therefore, as the referee suggested, the more interesting question is whether the existence of a linear continuous surjection
![]() $T:C_p(X)\to C_p(Y)$
implies the existence of another linear continuous surjection
$T:C_p(X)\to C_p(Y)$
implies the existence of another linear continuous surjection
![]() $S:C_p(X)\to C_p(Y)$
which is c-good for some
$S:C_p(X)\to C_p(Y)$
which is c-good for some
![]() $c>0$
. In that connection, let us note that more general notion was considered in our recent paper [Reference Eysen, Leiderman and Valov3]:
$c>0$
. In that connection, let us note that more general notion was considered in our recent paper [Reference Eysen, Leiderman and Valov3]:
![]() $T:D_p(X)\to D_p(Y)$
is inversely bounded if for every norm bounded sequence
$T:D_p(X)\to D_p(Y)$
is inversely bounded if for every norm bounded sequence
![]() $\{g_n\}\subset C^*(Y)$
there exists a norm bounded sequence
$\{g_n\}\subset C^*(Y)$
there exists a norm bounded sequence
![]() $\{f_n\}\subset C^*(X)$
with
$\{f_n\}\subset C^*(X)$
with
![]() $T(f_n)=g_n$
for all n. Evidently, every c-good map is inversely bounded. It was established in [Reference Eysen, Leiderman and Valov3] that uniformly continuous inversely bounded surjections
$T(f_n)=g_n$
for all n. Evidently, every c-good map is inversely bounded. It was established in [Reference Eysen, Leiderman and Valov3] that uniformly continuous inversely bounded surjections
![]() $T:D_p(X)\to D_p(Y)$
, where X and Y are metrizable, preserve any one of the properties zero-dimensionality, countable-dimensionality, or strong countable-dimensionality. Most probably Theorem 1.1 remains true if the surjection T is uniformly continuous and inversely bounded.
$T:D_p(X)\to D_p(Y)$
, where X and Y are metrizable, preserve any one of the properties zero-dimensionality, countable-dimensionality, or strong countable-dimensionality. Most probably Theorem 1.1 remains true if the surjection T is uniformly continuous and inversely bounded.
Finally, here is the theorem which provides a positive answer to the question of Kawamura–Leiderman [Reference Kawamura and Leiderman10, Problem 3.1] mentioned above.
Theorem 1.4 Let
![]() $T:C_p(X)\to C_p(Y)$
be a linear continuous surjection. If
$T:C_p(X)\to C_p(Y)$
be a linear continuous surjection. If
![]() $\dim X=0$
, then
$\dim X=0$
, then
![]() $\dim Y=0$
.
$\dim Y=0$
.
2 Preliminary results
In this section, we prove Proposition 2.1 which is used in the proofs of Theorems 1.1 and 1.3. Our proof is based on the idea of support introduced by Gul’ko [Reference Gul’ko7] and the extension of this notion introduced by Krupski [Reference Krupski12].
Let
![]() $\mathbb Q$
be the set of rational numbers. A subspace
$\mathbb Q$
be the set of rational numbers. A subspace
![]() $E(X)\subset C(X)$
is called a
$E(X)\subset C(X)$
is called a
![]() $QS$
-algebra [Reference Gul’ko7] if it satisfies the following conditions: (i) if
$QS$
-algebra [Reference Gul’ko7] if it satisfies the following conditions: (i) if
![]() $f,g\in E(X)$
and
$f,g\in E(X)$
and
![]() $\lambda \in \mathbb Q$
, then all functions
$\lambda \in \mathbb Q$
, then all functions
![]() $f+g$
,
$f+g$
,
![]() $f\cdot g$
, and
$f\cdot g$
, and
![]() $\lambda f$
belong to
$\lambda f$
belong to
![]() $E(X)$
and (ii) for every
$E(X)$
and (ii) for every
![]() $x\in X$
and its neighborhood U in X there is
$x\in X$
and its neighborhood U in X there is
![]() $f\in E(X)$
such that
$f\in E(X)$
such that
![]() $f(x)=1$
and
$f(x)=1$
and
![]() $f(X\backslash U)=0$
.
$f(X\backslash U)=0$
.
We are using the following facts from [Reference Gul’ko7].
-
(2.1) If X has a countable base and
 $\Phi \subset C(X)$
is a countable set, then there is a countable
$\Phi \subset C(X)$
is a countable set, then there is a countable
 $QS$
-algebra
$QS$
-algebra
 $E(X)\subset C(X)$
containing
$E(X)\subset C(X)$
containing
 $\Phi $
. Moreover, it follows from the proof of [Reference Gul’ko7, Proposition 1.2] that
$\Phi $
. Moreover, it follows from the proof of [Reference Gul’ko7, Proposition 1.2] that
 $E(X)\subset C^*(X)$
provided that
$E(X)\subset C^*(X)$
provided that
 $\Phi \subset C^*(X)$
.
$\Phi \subset C^*(X)$
. -
(2.2) If U is an open set in X,
 $x_1,x_2,\ldots ,x_k\in U$
and
$x_1,x_2,\ldots ,x_k\in U$
and
 $\lambda _1,\lambda _2,\ldots ,\lambda _k\in \mathbb Q$
, then there exists
$\lambda _1,\lambda _2,\ldots ,\lambda _k\in \mathbb Q$
, then there exists
 $f\in E(X)$
such that
$f\in E(X)$
such that
 $f(x_i)=\lambda _i$
for each i and
$f(x_i)=\lambda _i$
for each i and
 $f(X\backslash U)=0$
.
$f(X\backslash U)=0$
. -
(2.3) We consider the following condition for a
 $QS$
-algebra
$QS$
-algebra
 $E(X)$
on X: For every compact set
$E(X)$
on X: For every compact set
 $K\subset X$
and an open set W containing K there exists
$K\subset X$
and an open set W containing K there exists
 $f\in E(X)$
with
$f\in E(X)$
with
 $f|K=1$
,
$f|K=1$
,
 $f|(X\backslash W)=0$
and
$f|(X\backslash W)=0$
and
 $f(x)\in [0,1]$
for all
$f(x)\in [0,1]$
for all
 $x\in X$
. Note that if X has a countable base
$x\in X$
. Note that if X has a countable base
 $\mathcal B$
, then there is a countable
$\mathcal B$
, then there is a countable
 $QS$
-algebra
$QS$
-algebra
 $E(X)$
on X satisfying that condition. Indeed, we can assume that
$E(X)$
on X satisfying that condition. Indeed, we can assume that
 $\mathcal B$
is closed under finite unions and find
$\mathcal B$
is closed under finite unions and find
 $U,V\in \mathcal B$
such that
$U,V\in \mathcal B$
such that
 $K\subset V\subset \overline V\subset U\subset \overline U\subset W$
. Then, consider the set
$K\subset V\subset \overline V\subset U\subset \overline U\subset W$
. Then, consider the set
 $\Phi $
of all functions
$\Phi $
of all functions
 $f_{U,V}:X\to [0,1]$
, where
$f_{U,V}:X\to [0,1]$
, where
 $\overline V\subset U$
with
$\overline V\subset U$
with
 $U,V\in \mathcal B$
, such that
$U,V\in \mathcal B$
, such that
 $f_{V,U}|\overline V=1$
and
$f_{V,U}|\overline V=1$
and
 $f_{V,U}|(X\backslash U)=0$
. According to
$f_{V,U}|(X\backslash U)=0$
. According to
 $(2.1)$
,
$(2.1)$
,
 $\Phi $
can be extended to a countable
$\Phi $
can be extended to a countable
 $QS$
-algebra
$QS$
-algebra
 $E(X)$
on X.
$E(X)$
on X.
Everywhere below, we denote by
![]() $\overline {\mathbb R}$
the extended real line
$\overline {\mathbb R}$
the extended real line
![]() $[-\infty ,\infty ]$
.
$[-\infty ,\infty ]$
.
Proposition 2.1 Let
![]() $\overline X$
and
$\overline X$
and
![]() $\overline Y$
be metrizable compactifications of X and Y, and
$\overline Y$
be metrizable compactifications of X and Y, and
![]() ${H\subset \overline X}$
be a
${H\subset \overline X}$
be a
![]() $\sigma $
-compact space containing X. Suppose
$\sigma $
-compact space containing X. Suppose
![]() $E(H)$
is a
$E(H)$
is a
![]() $QS$
-algebra on H satisfying condition (2.3),
$QS$
-algebra on H satisfying condition (2.3),
![]() $E(X)=\{\overline f|X:\overline f\in E(H)\}$
and
$E(X)=\{\overline f|X:\overline f\in E(H)\}$
and
![]() $E(Y)\subset C(Y)$
is a family such that every
$E(Y)\subset C(Y)$
is a family such that every
![]() $g\in E(Y)$
is extendable to a map
$g\in E(Y)$
is extendable to a map
![]() $\overline g:\overline Y\to \overline {\mathbb R}$
and
$\overline g:\overline Y\to \overline {\mathbb R}$
and
![]() $E(\overline Y)=\{\overline g:g\in E(Y)\}$
contains a
$E(\overline Y)=\{\overline g:g\in E(Y)\}$
contains a
![]() $QS$
-algebra on
$QS$
-algebra on
![]() $\overline Y$
. Let also
$\overline Y$
. Let also
![]() $\varphi :E_p(X)\to E_p(Y)$
be a uniformly continuous surjection which is c-good for some
$\varphi :E_p(X)\to E_p(Y)$
be a uniformly continuous surjection which is c-good for some
![]() $c>0$
.
$c>0$
.
If all finite powers of H have a property
![]() $\mathcal P$
satisfying conditions (a)–(c), then there exists a
$\mathcal P$
satisfying conditions (a)–(c), then there exists a
![]() $\sigma $
-compact set
$\sigma $
-compact set
![]() $Y_\infty \subset \overline Y$
containing Y such that all finite powers of
$Y_\infty \subset \overline Y$
containing Y such that all finite powers of
![]() $Y_\infty $
have the same property
$Y_\infty $
have the same property
![]() $\mathcal P$
.
$\mathcal P$
.
Proof We fix a countable base
![]() $\mathcal B$
of H which is closed under finite unions, and denote by f the restriction
$\mathcal B$
of H which is closed under finite unions, and denote by f the restriction
![]() $\overline f|X$
of any
$\overline f|X$
of any
![]() $\overline f\in E(H)$
. For every
$\overline f\in E(H)$
. For every
![]() $y\in \overline Y$
, there is a map
$y\in \overline Y$
, there is a map
![]() $\alpha _y:E(H)\to \overline {\mathbb R}$
,
$\alpha _y:E(H)\to \overline {\mathbb R}$
,
![]() $\alpha _y(\overline f)=\overline {\varphi (f)}(y)$
. Since
$\alpha _y(\overline f)=\overline {\varphi (f)}(y)$
. Since
![]() $\varphi $
is uniformly continuous, so is the map
$\varphi $
is uniformly continuous, so is the map
![]() $\beta _y:E_p(X)\to \mathbb R$
,
$\beta _y:E_p(X)\to \mathbb R$
,
![]() $\beta _y(f)=\varphi (f)(y)$
. Let
$\beta _y(f)=\varphi (f)(y)$
. Let
![]() $H=\bigcup _kH_k$
be the union of an increasing sequence
$H=\bigcup _kH_k$
be the union of an increasing sequence
![]() $\{H_k\}$
of compact sets. Following Krupski [Reference Krupski12], for every
$\{H_k\}$
of compact sets. Following Krupski [Reference Krupski12], for every
![]() $y\in \overline Y$
and every
$y\in \overline Y$
and every
![]() $p,k\in \mathbb N$
, we define the families
$p,k\in \mathbb N$
, we define the families
and
where
Possibly, some or both of the values
![]() $\alpha _y(\overline f),\alpha _y(\overline g)$
from the definition of
$\alpha _y(\overline f),\alpha _y(\overline g)$
from the definition of
![]() $a(y,K)$
could be
$a(y,K)$
could be
![]() $\pm \infty $
. That’s why we use the following agreements:
$\pm \infty $
. That’s why we use the following agreements:
-
(2.4)
 $\infty +\infty =\infty , \infty -\infty =-\infty +\infty =0, -\infty -\infty =-\infty .$
$\infty +\infty =\infty , \infty -\infty =-\infty +\infty =0, -\infty -\infty =-\infty .$
Note that
![]() $a(y,\varnothing )=\infty $
since
$a(y,\varnothing )=\infty $
since
![]() $\varphi $
is surjective.
$\varphi $
is surjective.
Using that
![]() $E(X)$
and
$E(X)$
and
![]() $E(H)$
are
$E(H)$
are
![]() $QS$
-algebras on X and H, and following the arguments from Krupski’s paper [Reference Krupski12] (see also the proofs of [Reference Gul’ko7, Proposition 1.4] and [Reference Marciszewski and Pelant16, Proposition 3.1]), one can establish the following claims (for the sake of completeness, we provide the proofs).
$QS$
-algebras on X and H, and following the arguments from Krupski’s paper [Reference Krupski12] (see also the proofs of [Reference Gul’ko7, Proposition 1.4] and [Reference Marciszewski and Pelant16, Proposition 3.1]), one can establish the following claims (for the sake of completeness, we provide the proofs).
Claim 1 For every
![]() $y\in Y$
, there is
$y\in Y$
, there is
![]() $p,k\in \mathbb N$
such that
$p,k\in \mathbb N$
such that
![]() $\mathcal A_p^k(y)$
contains a finite nonempty subset of X.
$\mathcal A_p^k(y)$
contains a finite nonempty subset of X.
This claim follows from the proof of [Reference Krupski12, Proposition 2.1]. Indeed, since
![]() $\varphi $
is uniformly continuous there is
$\varphi $
is uniformly continuous there is
![]() $p\in \mathbb N$
and a finite set
$p\in \mathbb N$
and a finite set
![]() $K\subset X$
such that if
$K\subset X$
such that if
![]() $f,g\in E(X)$
and
$f,g\in E(X)$
and
![]() $|f(x)-g(x)|<1/p$
for every
$|f(x)-g(x)|<1/p$
for every
![]() $x\in K$
, then
$x\in K$
, then
![]() $|\alpha _y(\overline f)-\alpha _y(\overline g)|=|\varphi (f)(y)-\varphi (g)(y)|<1$
. Take arbitrary
$|\alpha _y(\overline f)-\alpha _y(\overline g)|=|\varphi (f)(y)-\varphi (g)(y)|<1$
. Take arbitrary
![]() $\overline f,\overline g\in E(H)$
with
$\overline f,\overline g\in E(H)$
with
![]() $|\overline f(x)-\overline g(x)|<1$
for every
$|\overline f(x)-\overline g(x)|<1$
for every
![]() $x\in K$
and consider the functions
$x\in K$
and consider the functions
![]() $\overline f_m=\overline f+ \frac {m}{p}(\overline g-\overline f)\in E(H)$
for each
$\overline f_m=\overline f+ \frac {m}{p}(\overline g-\overline f)\in E(H)$
for each
![]() $m=0,1,\ldots ,p$
. Obviously
$m=0,1,\ldots ,p$
. Obviously
![]() $|f_m(x)-f_{m+1}(x)|<1/p$
for all
$|f_m(x)-f_{m+1}(x)|<1/p$
for all
![]() $x\in K$
, so
$x\in K$
, so
![]() $|\alpha _y(\overline f_m)-\alpha _y(\overline f_{m+1})|<1$
. Consequently,
$|\alpha _y(\overline f_m)-\alpha _y(\overline f_{m+1})|<1$
. Consequently,
![]() $|\alpha _y(\overline f)-\alpha _y(\overline g)|\leq \sum _{m=0}^{p-1}|\alpha _y(\overline f_m)-\alpha _y(\overline f_{m+1})|<p$
. Because K is finite, there is
$|\alpha _y(\overline f)-\alpha _y(\overline g)|\leq \sum _{m=0}^{p-1}|\alpha _y(\overline f_m)-\alpha _y(\overline f_{m+1})|<p$
. Because K is finite, there is
![]() $k\in \mathbb N$
with
$k\in \mathbb N$
with
![]() $K\subset H_k$
. Hence,
$K\subset H_k$
. Hence,
![]() $K\in \mathcal A_p^k(y)$
.
$K\in \mathcal A_p^k(y)$
.
Consider the sets
![]() $Y_p^k=\{y\in \overline Y:\mathcal A_p^k(y)\neq \varnothing \}$
,
$Y_p^k=\{y\in \overline Y:\mathcal A_p^k(y)\neq \varnothing \}$
,
![]() $p,k\in \mathbb N$
.
$p,k\in \mathbb N$
.
Claim 2 Each
![]() $Y_p^k$
is a closed subset of
$Y_p^k$
is a closed subset of
![]() $\overline Y$
.
$\overline Y$
.
We use the proof of [Reference Krupski12, Lemma 2.2]. Suppose
![]() $y\not \in Y_p^k$
. Since
$y\not \in Y_p^k$
. Since
![]() $y\in Y_p^k$
iff
$y\in Y_p^k$
iff
![]() $H_k\in \mathcal A_p^k(y)$
,
$H_k\in \mathcal A_p^k(y)$
,
![]() $H_k\not \in \mathcal A_p^k(y)$
. So, there exist
$H_k\not \in \mathcal A_p^k(y)$
. So, there exist
![]() $\overline f,\overline g\in E(H)$
with
$\overline f,\overline g\in E(H)$
with
![]() $|\overline f(x)-\overline g(x)|<1$
for all
$|\overline f(x)-\overline g(x)|<1$
for all
![]() $x\in H_k$
and
$x\in H_k$
and
![]() $|\alpha _y(\overline f)-\alpha _y(\overline g)|>p$
. Then,
$|\alpha _y(\overline f)-\alpha _y(\overline g)|>p$
. Then,
![]() $V=\{z\in \overline Y: |\alpha _z(\overline f)-\alpha _z(\overline g)|>p\}$
is a neighborhood of y with
$V=\{z\in \overline Y: |\alpha _z(\overline f)-\alpha _z(\overline g)|>p\}$
is a neighborhood of y with
![]() $V\cap Y_p^k=\varnothing $
.
$V\cap Y_p^k=\varnothing $
.
Claim 3 Every set
![]() $Y_{p,q}^k=\{y\in Y_p^k: \exists K\in \mathcal A_p^k(y){~}\mbox {with}{~}|K|\leq q\}$
,
$Y_{p,q}^k=\{y\in Y_p^k: \exists K\in \mathcal A_p^k(y){~}\mbox {with}{~}|K|\leq q\}$
,
![]() $p,q,k\in \mathbb N$
, is closed in
$p,q,k\in \mathbb N$
, is closed in
![]() $Y_p^k$
.
$Y_p^k$
.
Following the proof of [Reference Krupski12, Lemma 2.3], we first show that the set
![]() $Z=\{(y,K)\in Y_p^k\times [H_k]^{\leq q}:K\in \mathcal A_p^k(y)\}$
is closed in
$Z=\{(y,K)\in Y_p^k\times [H_k]^{\leq q}:K\in \mathcal A_p^k(y)\}$
is closed in
![]() $Y_p^k\times [H_k]^{\leq q}$
, where
$Y_p^k\times [H_k]^{\leq q}$
, where
![]() $[H_k]^{\leq q}$
denotes the space of all subsets
$[H_k]^{\leq q}$
denotes the space of all subsets
![]() $K\subset H_k$
of cardinality
$K\subset H_k$
of cardinality
![]() $\leq q$
endowed with the Vietoris topology. Indeed, if
$\leq q$
endowed with the Vietoris topology. Indeed, if
![]() $(y,K)\in Y_p^k\times [H_k]^{\leq q}\backslash Z$
, then
$(y,K)\in Y_p^k\times [H_k]^{\leq q}\backslash Z$
, then
![]() $K\not \in \mathcal A_p^k(y)$
. Hence,
$K\not \in \mathcal A_p^k(y)$
. Hence,
![]() $a(y,K)>p$
and there are
$a(y,K)>p$
and there are
![]() $\overline f,\overline g\in E(H)$
such that
$\overline f,\overline g\in E(H)$
such that
![]() $|\overline f(x)-\overline g(x)|<1$
for all
$|\overline f(x)-\overline g(x)|<1$
for all
![]() $x\in K$
and
$x\in K$
and
![]() $|\alpha _y(\overline f)-\alpha _y(\overline g)|>p$
. Let
$|\alpha _y(\overline f)-\alpha _y(\overline g)|>p$
. Let
![]() $U=\{z\in Y_p^k: |\alpha _z(\overline f)-\alpha _z(\overline g)|>p\}$
and
$U=\{z\in Y_p^k: |\alpha _z(\overline f)-\alpha _z(\overline g)|>p\}$
and
![]() $V=\{x\in H_k:|\overline f(x)-\overline g(x)|<1\}$
. The set
$V=\{x\in H_k:|\overline f(x)-\overline g(x)|<1\}$
. The set
![]() $U\times <V>$
is a neighborhood of
$U\times <V>$
is a neighborhood of
![]() $(y,K)$
in
$(y,K)$
in
![]() $Y_p^k\times [H_k]^{\leq q}$
disjoint from Z (here
$Y_p^k\times [H_k]^{\leq q}$
disjoint from Z (here
![]() $<V>=\{F\in [H_k]^{\leq q}: F\subset V\}$
). Since
$<V>=\{F\in [H_k]^{\leq q}: F\subset V\}$
). Since
![]() $Y_p^k\times [H_k]^{\leq q}$
is compact and
$Y_p^k\times [H_k]^{\leq q}$
is compact and
![]() $Y_{p,q}^k$
is the image of Z under the projection
$Y_{p,q}^k$
is the image of Z under the projection
![]() $Y_p^k\times [H_k]^{\leq q}\to Y_p^k$
,
$Y_p^k\times [H_k]^{\leq q}\to Y_p^k$
,
![]() $Y_{p,q}^k$
is closed in
$Y_{p,q}^k$
is closed in
![]() $Y_p^k$
.
$Y_p^k$
.
For every k, let
![]() $Y_k=\bigcup _{p,q}Y_{p,q}^k$
. Obviously,
$Y_k=\bigcup _{p,q}Y_{p,q}^k$
. Obviously,
![]() $Y_k\subset \{y\in \overline Y:\mathcal A^k(y)\neq \varnothing \}$
. Since
$Y_k\subset \{y\in \overline Y:\mathcal A^k(y)\neq \varnothing \}$
. Since
![]() ${H_k\subset H_{k+1}}$
for all k, the sequence
${H_k\subset H_{k+1}}$
for all k, the sequence
![]() $\{Y_k\}$
is increasing. It may happen that
$\{Y_k\}$
is increasing. It may happen that
![]() $Y_k=\varnothing $
for some k, but Claim 1 implies that
$Y_k=\varnothing $
for some k, but Claim 1 implies that
![]() $Y\subset \bigcup _{k}Y_{k}$
.
$Y\subset \bigcup _{k}Y_{k}$
.
Claim 4 For every
![]() $y\in Y_k$
, the family
$y\in Y_k$
, the family
![]() $\mathcal A^k(y)$
is closed under finite intersections and
$\mathcal A^k(y)$
is closed under finite intersections and
![]() $a(y,K_1\cap K_2)\leq a(y,K_1)+a(y,K_2)$
for all
$a(y,K_1\cap K_2)\leq a(y,K_1)+a(y,K_2)$
for all
![]() $K_1,K_2\in \mathcal A^k(y)$
.
$K_1,K_2\in \mathcal A^k(y)$
.
We follow the proof of [Reference Krupski12, Lemma 2.5] to show that
![]() $K_1\cap K_2\in \mathcal A^k(y)$
for any
$K_1\cap K_2\in \mathcal A^k(y)$
for any
![]() $K_1,K_2\in \mathcal A^k(y)$
. Let
$K_1,K_2\in \mathcal A^k(y)$
. Let
![]() $\overline f,\overline g\in E(H)$
with
$\overline f,\overline g\in E(H)$
with
![]() $|\overline f(x)-\overline g(x)|<1$
for all
$|\overline f(x)-\overline g(x)|<1$
for all
![]() $x\in K_1\cap K_2$
and
$x\in K_1\cap K_2$
and
![]() $U=\{x\in H:|\overline f(x)-\overline g(x)|<1\}$
. Take an open set W in H containing
$U=\{x\in H:|\overline f(x)-\overline g(x)|<1\}$
. Take an open set W in H containing
![]() $K_1$
with
$K_1$
with
![]() $W\cap K_2\subset U$
and choose
$W\cap K_2\subset U$
and choose
![]() $\overline u\in E(H)$
such that
$\overline u\in E(H)$
such that
![]() $\overline u|K_1=1$
,
$\overline u|K_1=1$
,
![]() $\overline u|(H\backslash W)=0$
and
$\overline u|(H\backslash W)=0$
and
![]() $\overline u(x)\in [0,1]$
for all
$\overline u(x)\in [0,1]$
for all
![]() $x\in H$
(see condition (2.3)). Then,
$x\in H$
(see condition (2.3)). Then,
![]() $\overline h=\overline u\cdot (\overline f-\overline g)+\overline g\in E(H)$
,
$\overline h=\overline u\cdot (\overline f-\overline g)+\overline g\in E(H)$
,
![]() $\overline h|K_1=\overline f|K_1$
,
$\overline h|K_1=\overline f|K_1$
,
![]() $\overline h|(K_2\backslash W)=\overline g|(K_2\backslash W)$
, and
$\overline h|(K_2\backslash W)=\overline g|(K_2\backslash W)$
, and
![]() $|\overline h(x)-\overline g(x)|<1$
for
$|\overline h(x)-\overline g(x)|<1$
for
![]() $x\in K_2$
. Since
$x\in K_2$
. Since
![]() $K_1\in \mathcal A^k(y)$
and
$K_1\in \mathcal A^k(y)$
and
![]() $\overline h|K_1=\overline f|K_1$
, we have
$\overline h|K_1=\overline f|K_1$
, we have
![]() $|\alpha _y(\overline f)-\alpha _y(\overline h)|\leq a(y,K_1)<\infty $
. Similarly,
$|\alpha _y(\overline f)-\alpha _y(\overline h)|\leq a(y,K_1)<\infty $
. Similarly,
![]() $K_2\in \mathcal A^k(y)$
and
$K_2\in \mathcal A^k(y)$
and
![]() $|\overline h(x)-\overline g(x)|<1$
for
$|\overline h(x)-\overline g(x)|<1$
for
![]() $x\in K_2$
imply
$x\in K_2$
imply
![]() $|\alpha _y(\overline h)-\alpha _y(\overline g)|\leq a(y,K_2)<\infty $
. Therefore,
$|\alpha _y(\overline h)-\alpha _y(\overline g)|\leq a(y,K_2)<\infty $
. Therefore,
Note that the last inequality is true if some of
![]() $\alpha _y(\overline f), \alpha _y(\overline h), \alpha _y(\overline g)$
are
$\alpha _y(\overline f), \alpha _y(\overline h), \alpha _y(\overline g)$
are
![]() $\pm \infty $
. Indeed, if
$\pm \infty $
. Indeed, if
![]() $\alpha _y(\overline f)=\pm \infty $
, then
$\alpha _y(\overline f)=\pm \infty $
, then
![]() $|\alpha _y(\overline f)-\alpha _y(\overline h)|<\infty $
implies
$|\alpha _y(\overline f)-\alpha _y(\overline h)|<\infty $
implies
![]() $\alpha _y(\overline h)=\pm \infty $
. Consequently,
$\alpha _y(\overline h)=\pm \infty $
. Consequently,
![]() ${\alpha _y(\overline g)=\pm \infty} $
because
${\alpha _y(\overline g)=\pm \infty} $
because
![]() $|\alpha _y(\overline h)-\alpha _y(\overline g)|<\infty $
. Similarly, if
$|\alpha _y(\overline h)-\alpha _y(\overline g)|<\infty $
. Similarly, if
![]() $\alpha _y(\overline h)=\pm \infty $
or
$\alpha _y(\overline h)=\pm \infty $
or
![]() $\alpha _y(\overline g)=\pm \infty $
, then the other two are also
$\alpha _y(\overline g)=\pm \infty $
, then the other two are also
![]() $\pm \infty $
. Hence,
$\pm \infty $
. Hence,
![]() $a(y,K_1\cap K_2)\leq a(y,K_1)+a(y,K_2)$
, which means that
$a(y,K_1\cap K_2)\leq a(y,K_1)+a(y,K_2)$
, which means that
![]() $K_1\cap K_2\neq \varnothing $
(otherwise,
$K_1\cap K_2\neq \varnothing $
(otherwise,
![]() $a(y,K_1\cap K_2)=\infty $
) and
$a(y,K_1\cap K_2)=\infty $
) and
![]() $K_1\cap K_2\in \mathcal A^k(y)$
.
$K_1\cap K_2\in \mathcal A^k(y)$
.
Since each family
![]() $\mathcal A^k(y)$
,
$\mathcal A^k(y)$
,
![]() $y\in Y_k$
, consists of compact subsets of
$y\in Y_k$
, consists of compact subsets of
![]() $H_k$
,
$H_k$
,
![]() $K(y,k)=\bigcap \mathcal A^k(y)$
is nonempty and compact.
$K(y,k)=\bigcap \mathcal A^k(y)$
is nonempty and compact.
Claim 5 For every
![]() $y\in Y_{k}$
, the set
$y\in Y_{k}$
, the set
![]() $K(y,k)$
is a nonempty finite subset of
$K(y,k)$
is a nonempty finite subset of
![]() $H_k$
with
$H_k$
with
![]() $K(y,k)\in \mathcal A^k(y)$
. Moreover, if
$K(y,k)\in \mathcal A^k(y)$
. Moreover, if
![]() $y\in Y$
, then there exists k such that
$y\in Y$
, then there exists k such that
![]() $y\in Y_k$
and
$y\in Y_k$
and
![]() ${K(y,k)\subset X}$
.
${K(y,k)\subset X}$
.
Let
![]() $y\in Y_k$
. We already observed that
$y\in Y_k$
. We already observed that
![]() $K(y,k)$
is compact and nonempty. Since
$K(y,k)$
is compact and nonempty. Since
![]() $y\in Y_{p,q}^k$
for some
$y\in Y_{p,q}^k$
for some
![]() $p,q$
,
$p,q$
,
![]() $\mathcal A^k(y)$
contains finite sets. Hence,
$\mathcal A^k(y)$
contains finite sets. Hence,
![]() $K(y,k)$
is also finite and
$K(y,k)$
is also finite and
![]() $K(y,k)\in \mathcal A^k(y)$
because it is an intersection of finitely many elements of
$K(y,k)\in \mathcal A^k(y)$
because it is an intersection of finitely many elements of
![]() $\mathcal A^k(y)$
. If
$\mathcal A^k(y)$
. If
![]() $y\in Y$
, then by Claim 1, there is k such that
$y\in Y$
, then by Claim 1, there is k such that
![]() $\mathcal A^k(y)$
contains a finite subset of X. Since
$\mathcal A^k(y)$
contains a finite subset of X. Since
![]() $K(y,k)$
is the minimal element of
$K(y,k)$
is the minimal element of
![]() $\mathcal A^k(y)$
, it is also a subset of X.
$\mathcal A^k(y)$
, it is also a subset of X.
Following [Reference Gul’ko7], for every k, we define
![]() $M^k(p,1)=Y_{p,1}^k$
and
$M^k(p,1)=Y_{p,1}^k$
and
![]() $M^k(p,q)=Y_{p,q}^k\backslash Y_{2p,q-1}^k$
if
$M^k(p,q)=Y_{p,q}^k\backslash Y_{2p,q-1}^k$
if
![]() $q\geq 2$
.
$q\geq 2$
.
Claim 6
![]() $Y_k=\bigcup \{M^k(p,q):p,q=1,2,\ldots \}$
and for every
$Y_k=\bigcup \{M^k(p,q):p,q=1,2,\ldots \}$
and for every
![]() $y\in M^k(p,q)$
, there exists a unique set
$y\in M^k(p,q)$
, there exists a unique set
![]() $K_{kp}(y)\in \mathcal A^k(y)$
of cardinality q such that
$K_{kp}(y)\in \mathcal A^k(y)$
of cardinality q such that
![]() $a(y,K_{kp}(y))\leq p$
.
$a(y,K_{kp}(y))\leq p$
.
Since
![]() $M^k(p,q)\subset Y^k_{p,q}\subset Y_k$
,
$M^k(p,q)\subset Y^k_{p,q}\subset Y_k$
,
![]() $\bigcup \{M^k(p,q):p,q=1,2,\ldots \}\subset Y_k$
. If
$\bigcup \{M^k(p,q):p,q=1,2,\ldots \}\subset Y_k$
. If
![]() $y\in Y_k$
, then
$y\in Y_k$
, then
![]() $K(y,k)\in \mathcal A^k(y)$
is a finite subset of
$K(y,k)\in \mathcal A^k(y)$
is a finite subset of
![]() $H_k$
. Assume
$H_k$
. Assume
![]() $|K(y,k)|=q$
and
$|K(y,k)|=q$
and
![]() $a(y,K(y,k))\leq p$
for some
$a(y,K(y,k))\leq p$
for some
![]() $p,q$
. So,
$p,q$
. So,
![]() $y\in Y_{p,q}^k$
. Moreover,
$y\in Y_{p,q}^k$
. Moreover,
![]() $y\not \in Y_{2p,q-1}^k$
, otherwise, there would be
$y\not \in Y_{2p,q-1}^k$
, otherwise, there would be
![]() $K\in \mathcal A^k(y)$
with
$K\in \mathcal A^k(y)$
with
![]() $a(y,K)\leq 2p$
and
$a(y,K)\leq 2p$
and
![]() $|K|\leq q-1$
. The last inequality contradicts the minimality of
$|K|\leq q-1$
. The last inequality contradicts the minimality of
![]() $K(y,k)$
. Hence,
$K(y,k)$
. Hence,
![]() $y\in M^k(p,q)$
which shows that
$y\in M^k(p,q)$
which shows that
![]() $Y_k=\bigcup \{M^k(p,q):p,q=1,2,\ldots \}$
.
$Y_k=\bigcup \{M^k(p,q):p,q=1,2,\ldots \}$
.
Suppose
![]() $y\in M^k(p,q)$
. Then, there exists a set
$y\in M^k(p,q)$
. Then, there exists a set
![]() $K\in \mathcal A^k(y)$
with
$K\in \mathcal A^k(y)$
with
![]() $a(y,K)\leq p$
and
$a(y,K)\leq p$
and
![]() $|K|\leq q$
. Since,
$|K|\leq q$
. Since,
![]() $y\not \in Y_{2p,q-1}^k$
,
$y\not \in Y_{2p,q-1}^k$
,
![]() $|K|=q$
. If there exists another
$|K|=q$
. If there exists another
![]() $K'\in \mathcal A^k(y)$
with
$K'\in \mathcal A^k(y)$
with
![]() $a(y,K')\leq p$
and
$a(y,K')\leq p$
and
![]() $|K'|=q$
, then
$|K'|=q$
, then
![]() $K\cap K'\neq \varnothing $
,
$K\cap K'\neq \varnothing $
,
![]() $|K\cap K'|\leq q-1$
and, by Claim 4,
$|K\cap K'|\leq q-1$
and, by Claim 4,
![]() $a(y,K\cap K')\leq a(y,K)+ a(y,K')\leq 2p$
. This means that
$a(y,K\cap K')\leq a(y,K)+ a(y,K')\leq 2p$
. This means that
![]() $y\in Y_{2p,q-1}^k$
, a contradiction. Hence, there exists a unique
$y\in Y_{2p,q-1}^k$
, a contradiction. Hence, there exists a unique
![]() $K_{kp}(y)\in \mathcal A^k(y)$
such that
$K_{kp}(y)\in \mathcal A^k(y)$
such that
![]() $a(y,K_{kp}(y))\leq p$
and
$a(y,K_{kp}(y))\leq p$
and
![]() $|K_{kp}(y)|=q$
.
$|K_{kp}(y)|=q$
.
For every q, let
![]() $[H_k]^q$
denote the set of all q-points subsets of
$[H_k]^q$
denote the set of all q-points subsets of
![]() $H_k$
endowed with the Vietoris topology.
$H_k$
endowed with the Vietoris topology.
Claim 7 The map
![]() $\Phi _{kpq}:M^k(p,q)\to [H_k]^q$
,
$\Phi _{kpq}:M^k(p,q)\to [H_k]^q$
,
![]() $\Phi _{kpq}(y)=K_{kp}(y)$
, is continuous.
$\Phi _{kpq}(y)=K_{kp}(y)$
, is continuous.
Because
![]() $K_{kp}(y)\subset H_k$
consists of q points for all
$K_{kp}(y)\subset H_k$
consists of q points for all
![]() $y\in M^k(p,q)$
, it suffices to show that if
$y\in M^k(p,q)$
, it suffices to show that if
![]() $K_{kp}(y)\cap U\neq \varnothing $
for some open
$K_{kp}(y)\cap U\neq \varnothing $
for some open
![]() $U\subset H$
, then there is a neighborhood V of y in
$U\subset H$
, then there is a neighborhood V of y in
![]() $\overline Y$
with
$\overline Y$
with
![]() $K_{kp}(z)\cap U\neq \varnothing $
for all
$K_{kp}(z)\cap U\neq \varnothing $
for all
![]() $z\in V\cap M^k(p,q)$
. We can assume that
$z\in V\cap M^k(p,q)$
. We can assume that
![]() $K_{kp}(y)\cap U$
contains exactly one point
$K_{kp}(y)\cap U$
contains exactly one point
![]() $x_0$
.
$x_0$
.
Let
![]() $q\geq 2$
, so
$q\geq 2$
, so
![]() $K_{kp}(y)=\{x_0,x_1,\ldots ,x_{q-1}\}$
. Since
$K_{kp}(y)=\{x_0,x_1,\ldots ,x_{q-1}\}$
. Since
![]() $y\not \in Y_{2p,q-1}^k$
we have
$y\not \in Y_{2p,q-1}^k$
we have
![]() $a(y,K)>2p$
, where
$a(y,K)>2p$
, where
![]() $K=\{x_1,\ldots ,x_{q-1}\}$
. Hence, there are
$K=\{x_1,\ldots ,x_{q-1}\}$
. Hence, there are
![]() $\overline f, \overline g\in E(H)$
such that
$\overline f, \overline g\in E(H)$
such that
![]() $|\overline f(x)-\overline g(x)|<1$
for all
$|\overline f(x)-\overline g(x)|<1$
for all
![]() $x\in K$
and
$x\in K$
and
![]() $|\alpha _y(\overline f)-\alpha _y(\overline g)|>2p$
. The last inequality implies
$|\alpha _y(\overline f)-\alpha _y(\overline g)|>2p$
. The last inequality implies
![]() $\overline f(x_0)\neq \overline g(x_0)$
, otherwise,
$\overline f(x_0)\neq \overline g(x_0)$
, otherwise,
![]() $a(y,K_{kp}(y))$
would be greater than
$a(y,K_{kp}(y))$
would be greater than
![]() $2p$
(recall that
$2p$
(recall that
![]() $y\in M^k(p,q)$
implies
$y\in M^k(p,q)$
implies
![]() $a(y,K_{kp}(y))\leq p$
). So, at least one of the numbers
$a(y,K_{kp}(y))\leq p$
). So, at least one of the numbers
![]() $\overline f(x_0), \overline g(x_0)$
is not zero. Without loss of generality, we can assume that
$\overline f(x_0), \overline g(x_0)$
is not zero. Without loss of generality, we can assume that
![]() $\overline f(x_0)>0$
, and let r be a rational number with
$\overline f(x_0)>0$
, and let r be a rational number with
![]() $\frac {-1+\delta }{\overline f(x_0)}<r<\frac {1+\delta }{\overline f(x_0)}$
, where
$\frac {-1+\delta }{\overline f(x_0)}<r<\frac {1+\delta }{\overline f(x_0)}$
, where
![]() $\delta =\overline f(x_0)-\overline g(x_0)$
. Then,
$\delta =\overline f(x_0)-\overline g(x_0)$
. Then,
![]() $-1<(1-r)\overline f(x_0)-\overline g(x_0)<1$
, and choose
$-1<(1-r)\overline f(x_0)-\overline g(x_0)<1$
, and choose
![]() $\overline h_1\in E(H)$
such that
$\overline h_1\in E(H)$
such that
![]() $\overline h_1(x_0)=r$
and
$\overline h_1(x_0)=r$
and
![]() $\overline h_1(x)=0$
for all
$\overline h_1(x)=0$
for all
![]() $x\not \in U$
. Consider the function
$x\not \in U$
. Consider the function
![]() $\overline h=(1-\overline h_1)\overline f$
. Clearly,
$\overline h=(1-\overline h_1)\overline f$
. Clearly,
![]() $\overline h(x_0)=(1-r)\overline f(x_0)$
and
$\overline h(x_0)=(1-r)\overline f(x_0)$
and
![]() $\overline h(x)=\overline f(x)$
if
$\overline h(x)=\overline f(x)$
if
![]() $x\not \in U$
. Hence,
$x\not \in U$
. Hence,
![]() $\overline h\in E(H)$
and
$\overline h\in E(H)$
and
![]() $|\overline h(x)-\overline g(x)|<1$
for all
$|\overline h(x)-\overline g(x)|<1$
for all
![]() $x\in K_{kp}(y)$
. This implies
$x\in K_{kp}(y)$
. This implies
![]() $|\alpha _y(\overline h)-\alpha _y(\overline g)|\leq p$
. Then,
$|\alpha _y(\overline h)-\alpha _y(\overline g)|\leq p$
. Then,
Observe that it is not possible
![]() $\alpha _y(\overline f)=\alpha _y(\overline h)=\pm \infty $
because
$\alpha _y(\overline f)=\alpha _y(\overline h)=\pm \infty $
because
![]() $|\alpha _y(\overline h)-\alpha _y(\overline g)|\leq p$
would imply
$|\alpha _y(\overline h)-\alpha _y(\overline g)|\leq p$
would imply
![]() $\alpha _y(\overline g)=\pm \infty $
. Then,
$\alpha _y(\overline g)=\pm \infty $
. Then,
![]() $|\alpha _y(\overline f)-\alpha _y(\overline g)|=0$
, a contradiction.
$|\alpha _y(\overline f)-\alpha _y(\overline g)|=0$
, a contradiction.
The set
![]() $V=\{z\in \overline Y:|\alpha _z(\overline f)-\alpha _z(\overline h)|>p\}$
is a neighborhood of y. Since
$V=\{z\in \overline Y:|\alpha _z(\overline f)-\alpha _z(\overline h)|>p\}$
is a neighborhood of y. Since
![]() $\overline h(x)=\overline f(x)$
for all
$\overline h(x)=\overline f(x)$
for all
![]() $x\not \in U$
,
$x\not \in U$
,
![]() $K_{kp}(z)\cap U=\varnothing $
for some
$K_{kp}(z)\cap U=\varnothing $
for some
![]() $z\in V\cap M^k(p,q)$
would imply
$z\in V\cap M^k(p,q)$
would imply
![]() $|\alpha _z(\overline h)-\alpha _z(\overline f)|\leq p$
, a contradiction. Therefore,
$|\alpha _z(\overline h)-\alpha _z(\overline f)|\leq p$
, a contradiction. Therefore,
![]() $K_{kp}(z)\cap U\neq \varnothing $
for
$K_{kp}(z)\cap U\neq \varnothing $
for
![]() $z\in V\cap M^k(p,q)$
.
$z\in V\cap M^k(p,q)$
.
If
![]() $q=1$
, then
$q=1$
, then
![]() $K_{kp}(y)=\{x_0\}$
and
$K_{kp}(y)=\{x_0\}$
and
![]() $K(y,k)=K_{kp}(y)$
. So,
$K(y,k)=K_{kp}(y)$
. So,
![]() $H_k\backslash U\not \in \mathcal A^k(y)$
(otherwise,
$H_k\backslash U\not \in \mathcal A^k(y)$
(otherwise,
![]() $K(y,k)\subset H_k\backslash U$
). Hence, there exist
$K(y,k)\subset H_k\backslash U$
). Hence, there exist
![]() $\overline f,\overline g\in E(H)$
such that
$\overline f,\overline g\in E(H)$
such that
![]() $|\overline f(x)-\overline g(x)|<1$
for all
$|\overline f(x)-\overline g(x)|<1$
for all
![]() $x\in H_k\backslash U$
and
$x\in H_k\backslash U$
and
![]() $|\alpha _y(\overline f)-\alpha _y(\overline g)|>2p$
. Define
$|\alpha _y(\overline f)-\alpha _y(\overline g)|>2p$
. Define
![]() $\overline h\in E(H)$
as in the previous case and use the same arguments to complete the proof.
$\overline h\in E(H)$
as in the previous case and use the same arguments to complete the proof.
Since
![]() $Y_{p,q}^k$
are compact subsets of
$Y_{p,q}^k$
are compact subsets of
![]() $\overline Y$
, each
$\overline Y$
, each
![]() $M^k(p,q)$
is a countable union of compact subsets
$M^k(p,q)$
is a countable union of compact subsets
![]() $\{F_n^k(p,q):n=1,2,\ldots \}$
of
$\{F_n^k(p,q):n=1,2,\ldots \}$
of
![]() $\overline Y$
. So, by Claim 6,
$\overline Y$
. So, by Claim 6,
![]() $Y_k=\bigcup \{F_n^k(p,q):n,p,q=1,2,\ldots \}$
. According to Claim 7, all maps
$Y_k=\bigcup \{F_n^k(p,q):n,p,q=1,2,\ldots \}$
. According to Claim 7, all maps
![]() $\Phi _{kpq}^n=\Phi _{kpq}|F_n^k(p,q):F_n^k(p,q)\to [H_k]^q$
are continuous. Moreover, since
$\Phi _{kpq}^n=\Phi _{kpq}|F_n^k(p,q):F_n^k(p,q)\to [H_k]^q$
are continuous. Moreover, since
![]() $Y\subset \bigcup _kY_k$
,
$Y\subset \bigcup _kY_k$
,
![]() $Y\subset \bigcup \{F_n^k(p,q):n,p,q,k=1,2,\ldots \}$
.
$Y\subset \bigcup \{F_n^k(p,q):n,p,q,k=1,2,\ldots \}$
.
Claim 8 The fibers of
![]() $\Phi _{kpq}^n:F_n^k(p,q)\to [H_k]^q$
are finite.
$\Phi _{kpq}^n:F_n^k(p,q)\to [H_k]^q$
are finite.
We follow the arguments from the proof of [Reference Gorak, Krupski and Marciszewski6, Theorem 4.2]. Fix
![]() $z\in F_n^k(p,q)$
for some
$z\in F_n^k(p,q)$
for some
![]() $n,p,q, k$
and let
$n,p,q, k$
and let
![]() $A=\{y\in F_n^k(p,q):K_{kp}(y)=K_{kp}(z)\}$
. Since
$A=\{y\in F_n^k(p,q):K_{kp}(y)=K_{kp}(z)\}$
. Since
![]() $\Phi _{kpq}^n$
is a perfect map, A is compact. Suppose A is infinite, so it contains a convergent sequence
$\Phi _{kpq}^n$
is a perfect map, A is compact. Suppose A is infinite, so it contains a convergent sequence
![]() $S=\{y_m\}$
of distinct points. Because
$S=\{y_m\}$
of distinct points. Because
![]() $E(\overline Y)$
contains a
$E(\overline Y)$
contains a
![]() $QS$
-algebra
$QS$
-algebra
![]() $\Gamma $
on
$\Gamma $
on
![]() $\overline Y$
, for every
$\overline Y$
, for every
![]() $y_m$
there exist its neighborhood
$y_m$
there exist its neighborhood
![]() $U_m$
in
$U_m$
in
![]() $\overline Y$
and a function
$\overline Y$
and a function
![]() $\overline g_m\in \Gamma $
,
$\overline g_m\in \Gamma $
,
![]() $\overline g_m:\overline Y\to [0,2p]$
such that:
$\overline g_m:\overline Y\to [0,2p]$
such that:
![]() $U_m\cap S=\{y_m\}$
,
$U_m\cap S=\{y_m\}$
,
![]() $\overline g_m(y_m)=2p$
, and
$\overline g_m(y_m)=2p$
, and
![]() $\overline g_m(y)=0$
for all
$\overline g_m(y)=0$
for all
![]() $y\not \in U_m$
. Since
$y\not \in U_m$
. Since
![]() $\varphi $
is c-good, for each m, there is
$\varphi $
is c-good, for each m, there is
![]() $f_m\in E(X)$
with
$f_m\in E(X)$
with
![]() $\varphi (f_m)=\overline g_m|Y=g_m$
and
$\varphi (f_m)=\overline g_m|Y=g_m$
and
![]() $||f_m||\leq c||g_m||$
. So,
$||f_m||\leq c||g_m||$
. So,
![]() $||\overline f_m||\leq 2pc$
,
$||\overline f_m||\leq 2pc$
,
![]() $m=1,2,\ldots $
and the sequence
$m=1,2,\ldots $
and the sequence
![]() $\{\overline f_m\}$
is contained in the compact set
$\{\overline f_m\}$
is contained in the compact set
![]() $[-2pc,2pc]^{H}$
. Hence,
$[-2pc,2pc]^{H}$
. Hence,
![]() $\{\overline f_m\}$
has an accumulation point in
$\{\overline f_m\}$
has an accumulation point in
![]() $[-2pc,2pc]^{H}$
. This implies the existence of
$[-2pc,2pc]^{H}$
. This implies the existence of
![]() $i\neq j$
such that
$i\neq j$
such that
![]() $|\overline f_i(x)-\overline f_j(x)|<1$
for all
$|\overline f_i(x)-\overline f_j(x)|<1$
for all
![]() $x\in K_{kp}(z)$
. Consequently, since
$x\in K_{kp}(z)$
. Consequently, since
![]() $K_{kp}(y_j)=K_{kp}(z)$
,
$K_{kp}(y_j)=K_{kp}(z)$
,
![]() $|\alpha _{y_j}(\overline f_j)-\alpha _{y_j}(\overline f_i)|\leq p$
. On the other hand,
$|\alpha _{y_j}(\overline f_j)-\alpha _{y_j}(\overline f_i)|\leq p$
. On the other hand,
![]() $\alpha _{y_j}(\overline f_j)=\overline {\varphi (f_j)}(y_j)=\overline g_j(y_j)=2p$
and
$\alpha _{y_j}(\overline f_j)=\overline {\varphi (f_j)}(y_j)=\overline g_j(y_j)=2p$
and
![]() $\alpha _{y_j}(\overline f_i)=\overline {\varphi (f_i)}(y_j)=\overline g_i(y_j)=0$
, so
$\alpha _{y_j}(\overline f_i)=\overline {\varphi (f_i)}(y_j)=\overline g_i(y_j)=0$
, so
![]() $|\alpha _{y_j}(\overline f_j)-\alpha _{y_j}(\overline f_i)|=2p$
, a contradiction.
$|\alpha _{y_j}(\overline f_j)-\alpha _{y_j}(\overline f_i)|=2p$
, a contradiction.
Now, we can complete the proof of Proposition 2.1. Suppose H has a property
![]() $\mathcal P$
satisfying conditions (a)–(c). Then so does
$\mathcal P$
satisfying conditions (a)–(c). Then so does
![]() $H_k^q$
for each
$H_k^q$
for each
![]() $k,q$
because
$k,q$
because
![]() $H_k^q$
is closed in
$H_k^q$
is closed in
![]() $H^q$
. We claim that the space
$H^q$
. We claim that the space
![]() $[H_k]^q$
also has the property
$[H_k]^q$
also has the property
![]() $\mathcal P$
. Indeed, let
$\mathcal P$
. Indeed, let
![]() $\mathcal C$
be a countable base of
$\mathcal C$
be a countable base of
![]() $H_k$
. For every q-tuple
$H_k$
. For every q-tuple
![]() $(U_1,\ldots ,U_q)$
of elements of
$(U_1,\ldots ,U_q)$
of elements of
![]() $\mathcal C$
with pairwise disjoint closures, the closed set
$\mathcal C$
with pairwise disjoint closures, the closed set
is homeomorphic to the closed subset
![]() $\overline U_1\times \cdots \times \overline U_q$
of
$\overline U_1\times \cdots \times \overline U_q$
of
![]() $H_k^q$
. Hence,
$H_k^q$
. Hence,
![]() $W(U_1,\ldots ,U_q)\in \mathcal P$
. Clearly, the space
$W(U_1,\ldots ,U_q)\in \mathcal P$
. Clearly, the space
![]() $[H_k]^q$
can be covered by countably many sets of the form
$[H_k]^q$
can be covered by countably many sets of the form
![]() $W(U_1,\ldots , U_q)$
, therefore, it belongs to
$W(U_1,\ldots , U_q)$
, therefore, it belongs to
![]() $\mathcal P$
. Finally, since the maps
$\mathcal P$
. Finally, since the maps
![]() $\Phi _{kpq}^n:F_n^k(p,q)\to [H_k]^q$
are perfect and have finite fibers, each
$\Phi _{kpq}^n:F_n^k(p,q)\to [H_k]^q$
are perfect and have finite fibers, each
![]() $F_n^k(p,q)$
has the property
$F_n^k(p,q)$
has the property
![]() $\mathcal P$
. Therefore, by condition (b),
$\mathcal P$
. Therefore, by condition (b),
![]() $Y_\infty =\bigcup \{F_n^k(p,q):n,p,q,k=1,2,\ldots \}$
has the property
$Y_\infty =\bigcup \{F_n^k(p,q):n,p,q,k=1,2,\ldots \}$
has the property
![]() $\mathcal P$
.
$\mathcal P$
.
It remains to show that all powers of
![]() $Y_\infty $
also have the property
$Y_\infty $
also have the property
![]() $\mathcal P$
. Simplifying the notations, we observed that
$\mathcal P$
. Simplifying the notations, we observed that
![]() $Y_\infty =\bigcup _{m=1}^\infty F_m$
, where every
$Y_\infty =\bigcup _{m=1}^\infty F_m$
, where every
![]() $F_m$
is a compact set admitting a map
$F_m$
is a compact set admitting a map
![]() $\Phi _m$
with finite fibers onto a compact subset of
$\Phi _m$
with finite fibers onto a compact subset of
![]() $H^m$
. Then, for every k, we have
$H^m$
. Then, for every k, we have
Consequently,
![]() $\prod _{i=1}^k\Phi _{m_i}:\prod _{i=1}^kF_{m_i}\to H^{m_1+m_2+\cdots +m_k}$
is a map which fibers are products of k-many finite sets. Hence, the fibers of
$\prod _{i=1}^k\Phi _{m_i}:\prod _{i=1}^kF_{m_i}\to H^{m_1+m_2+\cdots +m_k}$
is a map which fibers are products of k-many finite sets. Hence, the fibers of
![]() $\prod _{i=1}^k\Phi _{m_i}$
are finite. Because
$\prod _{i=1}^k\Phi _{m_i}$
are finite. Because
![]() $H^{m_1+m_2+\cdots +m_k}\in \mathcal P$
, so is
$H^{m_1+m_2+\cdots +m_k}\in \mathcal P$
, so is
![]() $\prod _{i=1}^kF_{m_i}$
. Finally, by property
$\prod _{i=1}^kF_{m_i}$
. Finally, by property
![]() $(b)$
,
$(b)$
,
![]() $Y_\infty ^k\in \mathcal P$
.
$Y_\infty ^k\in \mathcal P$
.
All definitions below, except that one of
![]() $(m-C)$
-spaces, can be found in [Reference Engelking2]. A normal space X is called strongly countable-dimensional if X can be represented as a countable union of closed finite-dimensional subspaces. Recall that a normal space X is weakly infinite-dimensional if for every sequence
$(m-C)$
-spaces, can be found in [Reference Engelking2]. A normal space X is called strongly countable-dimensional if X can be represented as a countable union of closed finite-dimensional subspaces. Recall that a normal space X is weakly infinite-dimensional if for every sequence
![]() $\{(A_i,B_i)\}$
of pairs of disjoint closed subsets of X there exist closed sets
$\{(A_i,B_i)\}$
of pairs of disjoint closed subsets of X there exist closed sets
![]() $L_1,L_2,\ldots $
such that
$L_1,L_2,\ldots $
such that
![]() $L_i$
is a partition between
$L_i$
is a partition between
![]() $A_i$
and
$A_i$
and
![]() $B_i$
and
$B_i$
and
![]() $\bigcap _iL_i=\varnothing $
. A normal space X is a C-space if for every sequence
$\bigcap _iL_i=\varnothing $
. A normal space X is a C-space if for every sequence
![]() $\{\mathcal G_i\}$
of open covers of X there exists a sequence
$\{\mathcal G_i\}$
of open covers of X there exists a sequence
![]() $\{\mathcal H_i\}$
of families of pairwise disjoint open subsets of X such that for
$\{\mathcal H_i\}$
of families of pairwise disjoint open subsets of X such that for
![]() $i=1,2,\ldots $
each member of
$i=1,2,\ldots $
each member of
![]() $\mathcal H_i$
is contained in a member of
$\mathcal H_i$
is contained in a member of
![]() $\mathcal G_i$
and the union
$\mathcal G_i$
and the union
![]() $\bigcup _i\mathcal H_i$
is a cover of X. The
$\bigcup _i\mathcal H_i$
is a cover of X. The
![]() $(m-C)$
-spaces, where
$(m-C)$
-spaces, where
![]() $m\geq 2$
is a natural number, were introduced by Fedorchuk [Reference Fedorchuk4]: A normal space X is an
$m\geq 2$
is a natural number, were introduced by Fedorchuk [Reference Fedorchuk4]: A normal space X is an
![]() $(m-C)$
-space if for any sequence
$(m-C)$
-space if for any sequence
![]() $\{\mathcal G_i\}$
of open covers of X such that each
$\{\mathcal G_i\}$
of open covers of X such that each
![]() $\mathcal G_i$
consists of at most m elements, there is a sequence of disjoint open families
$\mathcal G_i$
consists of at most m elements, there is a sequence of disjoint open families
![]() $\{\mathcal H_i\}$
such that each
$\{\mathcal H_i\}$
such that each
![]() $\mathcal H_i$
refines
$\mathcal H_i$
refines
![]() $\mathcal G_i$
and
$\mathcal G_i$
and
![]() $\bigcup _i\mathcal H_i$
is a cover of X. The
$\bigcup _i\mathcal H_i$
is a cover of X. The
![]() $(2-C)$
-spaces are exactly the weakly infinite-dimensional spaces and for every m we have the inclusion
$(2-C)$
-spaces are exactly the weakly infinite-dimensional spaces and for every m we have the inclusion
![]() $(m+1)-C\subset m-C$
. Moreover, every C-space is
$(m+1)-C\subset m-C$
. Moreover, every C-space is
![]() $m-C$
for all m.
$m-C$
for all m.
It is well known that the class of metrizable strongly countable-dimensional spaces contains all finite-dimensional metrizable spaces and is contained in the class of metrizable C-spaces. The last inclusion follows from the following two facts: (i) every finite-dimensional paracompact space is a C-space [Reference Engelking2, Theorem 6.3.7] and (ii) every paracompact space which is a countable union of its closed C-spaces is also a C-space [Reference Gutev and Valov8, Theorem 4.1]. Moreover, every C-space is weakly infinite-dimensional [Reference Engelking2, Theorem 6.3.10].
In the class of
![]() $\sigma $
-compact metrizable spaces, the zero-dimensionality satisfies all conditions (a)–(c), see Theorems 1.5.16, 1.2.2, and 1.12.4 from [Reference Engelking2]. The strong countable-dimensionality also satisfies all these conditions, condition (c) follows easily from [Reference Engelking2, Theorem 1.12.4]. For C-space, this follows from mentioned above fact that a countable union of closed compact C-spaces is a C-space [Reference Gutev and Valov8, Theorem 4.1] and the following results of Hattori–Yamada [Reference Hattori and Yamada9]: the class of compact C-spaces is closed under finite products any perfect preimage of a C-space with C-space fibers is a C-space. Finally, if a
$\sigma $
-compact metrizable spaces, the zero-dimensionality satisfies all conditions (a)–(c), see Theorems 1.5.16, 1.2.2, and 1.12.4 from [Reference Engelking2]. The strong countable-dimensionality also satisfies all these conditions, condition (c) follows easily from [Reference Engelking2, Theorem 1.12.4]. For C-space, this follows from mentioned above fact that a countable union of closed compact C-spaces is a C-space [Reference Gutev and Valov8, Theorem 4.1] and the following results of Hattori–Yamada [Reference Hattori and Yamada9]: the class of compact C-spaces is closed under finite products any perfect preimage of a C-space with C-space fibers is a C-space. Finally, if a
![]() $\sigma $
-compact space X is weakly infinite-dimensional, then obviously every closed subset of X, as well as any countable union of closed subsets of X have the same property (see [Reference Engelking2, Theorem 6.1.6]). Condition (c) follows from the following result of Pol [Reference Pol19, Theorem 4.1]: If
$\sigma $
-compact space X is weakly infinite-dimensional, then obviously every closed subset of X, as well as any countable union of closed subsets of X have the same property (see [Reference Engelking2, Theorem 6.1.6]). Condition (c) follows from the following result of Pol [Reference Pol19, Theorem 4.1]: If
![]() $f:X\to Y$
is a continuous map between compact metrizable spaces such that Y is weakly infinite-dimensional and each fiber
$f:X\to Y$
is a continuous map between compact metrizable spaces such that Y is weakly infinite-dimensional and each fiber
![]() $f^{-1}(y)$
,
$f^{-1}(y)$
,
![]() $y\in Y$
, is at most countable, then X is weakly infinite-dimensional. The validity of conditions (a)–(c) for
$y\in Y$
, is at most countable, then X is weakly infinite-dimensional. The validity of conditions (a)–(c) for
![]() $(m-C)$
-spaces in the class of
$(m-C)$
-spaces in the class of
![]() $\sigma $
-compact metrizable spaces follows from the following results [Reference Fedorchuk4]: The
$\sigma $
-compact metrizable spaces follows from the following results [Reference Fedorchuk4]: The
![]() $(m-C)$
-space property is hereditary with respect to closed subsets, a countable union of closed
$(m-C)$
-space property is hereditary with respect to closed subsets, a countable union of closed
![]() $(m-C)$
-spaces is also
$(m-C)$
-spaces is also
![]() $m-C$
. Moreover, for
$m-C$
. Moreover, for
![]() $(m-C)$
-spaces, Krupski [Reference Krupski11, Lemma 4.5] established an analog of the cited above Pol’s result. Therefore, condition (c) holds for the property
$(m-C)$
-spaces, Krupski [Reference Krupski11, Lemma 4.5] established an analog of the cited above Pol’s result. Therefore, condition (c) holds for the property
![]() $m-C$
in the class of
$m-C$
in the class of
![]() $\sigma $
-compact metrizable spaces.
$\sigma $
-compact metrizable spaces.
3 Uniformly continuous surjections
In this section, we prove Theorems 1.1 and 1.3.
For every space X, let
![]() $\mathcal F_X$
be the class of all maps from X onto second countable spaces. For any two maps
$\mathcal F_X$
be the class of all maps from X onto second countable spaces. For any two maps
![]() $h_1,h_2\in \mathcal F_X$
, we write
$h_1,h_2\in \mathcal F_X$
, we write
![]() $h_1\succ h_2$
if there exists a continuous map
$h_1\succ h_2$
if there exists a continuous map
![]() $\theta :h_1(X)\to h_2(X)$
with
$\theta :h_1(X)\to h_2(X)$
with
![]() $h_2=\theta \circ h_1$
. If
$h_2=\theta \circ h_1$
. If
![]() $\Phi \subset C(X)$
, we denote by
$\Phi \subset C(X)$
, we denote by
![]() $\triangle \Phi $
the diagonal product of all
$\triangle \Phi $
the diagonal product of all
![]() $f\in \Phi $
. Clearly,
$f\in \Phi $
. Clearly,
![]() $(\triangle \Phi )(X)$
is a subspace of the product
$(\triangle \Phi )(X)$
is a subspace of the product
![]() $\prod \{\mathbb R_f:f\in \Phi \}$
, and let
$\prod \{\mathbb R_f:f\in \Phi \}$
, and let
![]() $\pi _f:(\triangle \Phi )(X)\to \mathbb R_f$
be the projection. Following [Reference Gul’ko7], we call a set
$\pi _f:(\triangle \Phi )(X)\to \mathbb R_f$
be the projection. Following [Reference Gul’ko7], we call a set
![]() $\Phi \subset C(X)$
admissible if the family
$\Phi \subset C(X)$
admissible if the family
![]() $\pi (\Phi )=\{\pi _f:f\in \Phi \}$
is a
$\pi (\Phi )=\{\pi _f:f\in \Phi \}$
is a
![]() $QS$
-algebra on
$QS$
-algebra on
![]() $(\triangle \Phi )(X)$
. We are using the following facts:
$(\triangle \Phi )(X)$
. We are using the following facts:
-
(3.1)
 $\dim X\leq n$
if and only if for every
$\dim X\leq n$
if and only if for every
 $h\in \mathcal F_X$
, there exists a
$h\in \mathcal F_X$
, there exists a
 $h_0\in \mathcal F_X$
such that
$h_0\in \mathcal F_X$
such that
 $\dim h_0(X)\leq n$
and
$\dim h_0(X)\leq n$
and
 $h_0\succ h$
[Reference Pestov18].
$h_0\succ h$
[Reference Pestov18]. -
(3.2) If
 $\dim X\leq n$
and
$\dim X\leq n$
and
 $\Phi \subset C(X)$
is countable, then there exists a countable set
$\Phi \subset C(X)$
is countable, then there exists a countable set
 ${\Theta \subset C(X)}$
containing
${\Theta \subset C(X)}$
containing
 $\Phi $
with
$\Phi $
with
 $\dim (\triangle \Theta )(X)\leq n$
. Moreover, it follows from the proof of [Reference Gul’ko7, Lemma 2.2] that we can choose
$\dim (\triangle \Theta )(X)\leq n$
. Moreover, it follows from the proof of [Reference Gul’ko7, Lemma 2.2] that we can choose
 $\Theta \subset C^*(X)$
provided that
$\Theta \subset C^*(X)$
provided that
 $\Phi \subset C^*(X)$
.
$\Phi \subset C^*(X)$
. -
(3.3) For every countable
 $\Phi '\subset C(X)$
, there is a countable admissible set
$\Phi '\subset C(X)$
, there is a countable admissible set
 $\Phi $
containing
$\Phi $
containing
 $\Phi '$
such that
$\Phi '$
such that
 $(\triangle \Phi )(X)$
is homeomorphic to
$(\triangle \Phi )(X)$
is homeomorphic to
 $(\triangle \Phi ')(X)$
. According to the proof of [Reference Gul’ko7, Lemma 2.4],
$(\triangle \Phi ')(X)$
. According to the proof of [Reference Gul’ko7, Lemma 2.4],
 $\Phi $
could be taken to be a subset of
$\Phi $
could be taken to be a subset of
 $C^*(X)$
if
$C^*(X)$
if
 $\Phi '\subset C^*(X)$
. Moreover, we can assume that
$\Phi '\subset C^*(X)$
. Moreover, we can assume that
 $\Phi '$
satisfies condition (2.3), so
$\Phi '$
satisfies condition (2.3), so
 $\pi (\Phi )$
also satisfies that condition.
$\pi (\Phi )$
also satisfies that condition. -
(3.4) If
 $\{\Psi _n\}$
is an increasing sequence of admissible subsets of
$\{\Psi _n\}$
is an increasing sequence of admissible subsets of
 $C(X)$
, then
$C(X)$
, then
 ${\Psi =\bigcup _n\Psi _n}$
is also admissible (see [Reference Gul’ko7, Lemma 2.5]).
${\Psi =\bigcup _n\Psi _n}$
is also admissible (see [Reference Gul’ko7, Lemma 2.5]).
We also need the following lemmas.
Lemma 3.1 Let X be a zero-dimensional separable metrizable space and
![]() $E(X)$
be a countable subfamily of
$E(X)$
be a countable subfamily of
![]() $C^*(X)$
. Then, there exists a metrizable zero-dimensional compactification
$C^*(X)$
. Then, there exists a metrizable zero-dimensional compactification
![]() $\overline X$
of X such that each
$\overline X$
of X such that each
![]() $f\in E(X)$
can be extended over
$f\in E(X)$
can be extended over
![]() $\overline X$
.
$\overline X$
.
Proof Let
![]() $X_0$
be a metrizable compactification of X and for every
$X_0$
be a metrizable compactification of X and for every
![]() $f\in E(X)$
denote by
$f\in E(X)$
denote by
![]() $Z_f$
the closure of
$Z_f$
the closure of
![]() $f(X)$
in
$f(X)$
in
![]() $\mathbb R$
. Consider the diagonal product h of the maps j and
$\mathbb R$
. Consider the diagonal product h of the maps j and
![]() $\triangle \{f:f\in E(X)\}$
, where
$\triangle \{f:f\in E(X)\}$
, where
![]() $j:X\hookrightarrow X_0$
is the embedding. Then, the closure
$j:X\hookrightarrow X_0$
is the embedding. Then, the closure
![]() $X_1$
of
$X_1$
of
![]() $h(X)$
in the product
$h(X)$
in the product
![]() $X_0\times \prod _{f\in E(X)}Z_f$
is a compactification of X such that every
$X_0\times \prod _{f\in E(X)}Z_f$
is a compactification of X such that every
![]() $f\in E(X)$
can be extended over
$f\in E(X)$
can be extended over
![]() $X_1$
. Let
$X_1$
. Let
![]() $\theta :\beta X\to X_1$
be the map witnessing that
$\theta :\beta X\to X_1$
be the map witnessing that
![]() $\beta X$
is a compactification of X larger than
$\beta X$
is a compactification of X larger than
![]() $X_1$
. Since
$X_1$
. Since
![]() $\dim \beta X=0$
, by the Mardešić factorization theorem [Reference Engelking2, Theorem 3.4.1] there is a metrizable compactum
$\dim \beta X=0$
, by the Mardešić factorization theorem [Reference Engelking2, Theorem 3.4.1] there is a metrizable compactum
![]() $\overline X$
and maps
$\overline X$
and maps
![]() $\nu :\beta X\to \overline X$
and
$\nu :\beta X\to \overline X$
and
![]() $\eta :\overline X\to X_1$
such that
$\eta :\overline X\to X_1$
such that
![]() $\dim \overline X=0$
and
$\dim \overline X=0$
and
![]() $\theta =\eta \circ \nu $
. Evidently,
$\theta =\eta \circ \nu $
. Evidently,
![]() $\nu |i(X)$
is a homeomorphism, where
$\nu |i(X)$
is a homeomorphism, where
![]() $i:X\hookrightarrow \beta X$
is the embedding, so
$i:X\hookrightarrow \beta X$
is the embedding, so
![]() $\overline X$
is a compactification of X. Because every
$\overline X$
is a compactification of X. Because every
![]() $f\in E(X)$
is extendable to a function
$f\in E(X)$
is extendable to a function
![]() $\overline f:X_1\to \mathbb R$
, the composition
$\overline f:X_1\to \mathbb R$
, the composition
![]() $\overline f\circ \eta $
is an extension of f over
$\overline f\circ \eta $
is an extension of f over
![]() $\overline X$
.
$\overline X$
.
Lemma 3.2 Let X be a separable metrizable space and
![]() $E(X)$
be a countable subfamily of
$E(X)$
be a countable subfamily of
![]() $C(X)$
. Then there exists a metrizable compactification
$C(X)$
. Then there exists a metrizable compactification
![]() $\overline X$
of X such that each
$\overline X$
of X such that each
![]() $f\in E(X)$
can be extended to a map
$f\in E(X)$
can be extended to a map
![]() $\overline f:\overline X\to \overline {\mathbb R}$
. Moreover, if
$\overline f:\overline X\to \overline {\mathbb R}$
. Moreover, if
![]() $\dim X=0$
, then we can assume that
$\dim X=0$
, then we can assume that
![]() $\dim \overline X=0$
.
$\dim \overline X=0$
.
Proof The proof is similar to the proof of Lemma 3.1. The only difference is that for every
![]() $f\in E(X)$
, we consider
$f\in E(X)$
, we consider
![]() $Z_f$
to be the closure of
$Z_f$
to be the closure of
![]() $f(X)$
in
$f(X)$
in
![]() $\overline {\mathbb R}$
.
$\overline {\mathbb R}$
.
Proof of Theorem 1.1
Let
![]() $T:D_p(X)\to D_p(Y)$
be a uniformly continuous c-good surjection. Everywhere below, for
$T:D_p(X)\to D_p(Y)$
be a uniformly continuous c-good surjection. Everywhere below, for
![]() $f\in C^*(X)$
, let
$f\in C^*(X)$
, let
![]() $\overline f\in C(\beta X)$
be its extension; similarly, if
$\overline f\in C(\beta X)$
be its extension; similarly, if
![]() $g\in C(Y)$
then
$g\in C(Y)$
then
![]() $\overline g\in C(\beta Y,\overline {\mathbb R})$
is the extension of g. According to
$\overline g\in C(\beta Y,\overline {\mathbb R})$
is the extension of g. According to
![]() $(3.1)$
, it suffices to prove that for every
$(3.1)$
, it suffices to prove that for every
![]() $h\in \mathcal F_{Y}$
, there is
$h\in \mathcal F_{Y}$
, there is
![]() $h_0\in \mathcal F_{Y}$
such that
$h_0\in \mathcal F_{Y}$
such that
![]() $\dim h_0(Y)=0$
and
$\dim h_0(Y)=0$
and
![]() ${h_0\succ h}$
. So, we fix
${h_0\succ h}$
. So, we fix
![]() $h\in \mathcal F_{Y}$
and let
$h\in \mathcal F_{Y}$
and let
![]() $\overline h:\beta Y\to \overline {h(Y)}$
be an extension of h, where
$\overline h:\beta Y\to \overline {h(Y)}$
be an extension of h, where
![]() $\overline {h(Y)}$
is a metrizable compactification of
$\overline {h(Y)}$
is a metrizable compactification of
![]() $h(Y)$
. We will construct by induction two sequences
$h(Y)$
. We will construct by induction two sequences
![]() $\{\Psi _n\}_{n\geq 1}\subset C(\beta X)$
and
$\{\Psi _n\}_{n\geq 1}\subset C(\beta X)$
and
![]() $\{\Phi _n\}_{n\geq 1}\subset C(\beta Y,\overline {\mathbb R})$
of countable sets, countable
$\{\Phi _n\}_{n\geq 1}\subset C(\beta Y,\overline {\mathbb R})$
of countable sets, countable
![]() $QS$
-algebras
$QS$
-algebras
![]() $\mathcal A_n$
on
$\mathcal A_n$
on
![]() $(\triangle \Psi _n)(\beta X)$
and countable
$(\triangle \Psi _n)(\beta X)$
and countable
![]() $QS$
-algebras
$QS$
-algebras
![]() $\Lambda _{n}$
on
$\Lambda _{n}$
on
![]() $Y_n'=(\triangle \Phi _n')(\beta Y)$
, where
$Y_n'=(\triangle \Phi _n')(\beta Y)$
, where
![]() $\Phi _n'=\{\overline {T(f)}:\overline f\in \Psi _n\}$
, satisfying the following conditions for every
$\Phi _n'=\{\overline {T(f)}:\overline f\in \Psi _n\}$
, satisfying the following conditions for every
![]() $n\geq 1$
:
$n\geq 1$
:
-
(3.5)
 $\Phi _1\subset C(\beta Y)$
is admissible and
$\Phi _1\subset C(\beta Y)$
is admissible and
 $\triangle \Phi _1\succ \overline h$
;
$\triangle \Phi _1\succ \overline h$
; -
(3.6)
 $\Phi _n\subset \Phi _{n+1}=\Phi _n'\cup \{\lambda \circ (\triangle \Phi _n'):\lambda \in \Lambda _{n}\}$
;
$\Phi _n\subset \Phi _{n+1}=\Phi _n'\cup \{\lambda \circ (\triangle \Phi _n'):\lambda \in \Lambda _{n}\}$
; -
(3.7) each
 $\Psi _n$
is admissible,
$\Psi _n$
is admissible,
 $\dim (\triangle \Psi _n)(\beta X)=0$
and
$\dim (\triangle \Psi _n)(\beta X)=0$
and
 $\Psi _n\subset \Psi _{n+1}$
;
$\Psi _n\subset \Psi _{n+1}$
; -
(3.8)
 $\mathcal A_n$
is a
$\mathcal A_n$
is a
 $QS$
-algebra on
$QS$
-algebra on
 $(\triangle \Psi _n)(\beta X)$
satisfying condition (2.3);
$(\triangle \Psi _n)(\beta X)$
satisfying condition (2.3); -
(3.9)
 $\Lambda _{n+1}$
contains
$\Lambda _{n+1}$
contains
 $\{\lambda \circ \delta _{n}:\lambda \in \Lambda _{n}\}$
, where
$\{\lambda \circ \delta _{n}:\lambda \in \Lambda _{n}\}$
, where
 $\delta _{n}:Y^{\prime }_{n+1}\to Y_{n}'$
is the surjective map generated by the inclusion
$\delta _{n}:Y^{\prime }_{n+1}\to Y_{n}'$
is the surjective map generated by the inclusion
 $\Phi _{n}'\subset \Phi _{n+1}'$
;
$\Phi _{n}'\subset \Phi _{n+1}'$
; -
(3.10) for every
 $\overline {g}\in \Phi _n\cap C(\beta Y),$
there is
$\overline {g}\in \Phi _n\cap C(\beta Y),$
there is
 $\overline f_g\in \Psi _{n}$
with
$\overline f_g\in \Psi _{n}$
with
 $||f_g||\leq c||g||$
and
$||f_g||\leq c||g||$
and
 $T(f_g)=g$
.
$T(f_g)=g$
.
Since
![]() $\overline h(\beta Y)$
is a separable metrizable space, by
$\overline h(\beta Y)$
is a separable metrizable space, by
![]() $(3.3)$
, there is a countable admissible set
$(3.3)$
, there is a countable admissible set
![]() $\Phi _1\subset C(\beta Y)$
with
$\Phi _1\subset C(\beta Y)$
with
![]() $\triangle \Phi _1\succ \overline h$
. Choose a countable set
$\triangle \Phi _1\succ \overline h$
. Choose a countable set
![]() $\Psi _1'\subset C(\beta X)$
such that for every
$\Psi _1'\subset C(\beta X)$
such that for every
![]() $\overline g\in \Phi _1$
, there is
$\overline g\in \Phi _1$
, there is
![]() $\overline f_g\in \Psi _1'$
with
$\overline f_g\in \Psi _1'$
with
![]() $||f_g||\leq c||g||$
and
$||f_g||\leq c||g||$
and
![]() $T(f_g)=g$
. Next, use
$T(f_g)=g$
. Next, use
![]() $(3.2)$
to find countable
$(3.2)$
to find countable
![]() $\Theta _1\subset C(\beta X)$
containing
$\Theta _1\subset C(\beta X)$
containing
![]() $\Psi _1'$
such that
$\Psi _1'$
such that
![]() $\dim (\triangle \Theta _1)(\beta X)=0$
. Finally, by
$\dim (\triangle \Theta _1)(\beta X)=0$
. Finally, by
![]() $(3.3)$
, we can extend
$(3.3)$
, we can extend
![]() $\Theta _1$
to a countable admissible set
$\Theta _1$
to a countable admissible set
![]() $\Psi _1\subset C(\beta X)$
such that
$\Psi _1\subset C(\beta X)$
such that
![]() $(\triangle \Psi _1)(\beta X)$
is homeomorphic to
$(\triangle \Psi _1)(\beta X)$
is homeomorphic to
![]() $(\triangle \Theta _1)(\beta X)$
and the
$(\triangle \Theta _1)(\beta X)$
and the
![]() $QS$
-algebra
$QS$
-algebra
![]() $\mathcal A_1=\pi (\Psi _1)$
on
$\mathcal A_1=\pi (\Psi _1)$
on
![]() $(\triangle \Psi _1)(\beta X)$
satisfies condition (2.3). Evidently,
$(\triangle \Psi _1)(\beta X)$
satisfies condition (2.3). Evidently,
![]() $\dim (\triangle \Psi _1)(\beta X)=0$
.
$\dim (\triangle \Psi _1)(\beta X)=0$
.
Suppose
![]() $\Phi _k$
and
$\Phi _k$
and
![]() $\Psi _k$
are already constructed for all
$\Psi _k$
are already constructed for all
![]() $k\leq n$
. Then,
$k\leq n$
. Then,
![]() $\Phi _{n}'=\{\overline {T(f)}:\overline f\in \Psi _n\}$
is a countable set in
$\Phi _{n}'=\{\overline {T(f)}:\overline f\in \Psi _n\}$
is a countable set in
![]() $C(\beta Y,\overline {\mathbb R})$
. Because
$C(\beta Y,\overline {\mathbb R})$
. Because
![]() $\Psi _{n-1}\subset \Psi _n$
,
$\Psi _{n-1}\subset \Psi _n$
,
![]() $\Phi _{n-1}'\subset \Phi _n'$
. So, there is a surjective map
$\Phi _{n-1}'\subset \Phi _n'$
. So, there is a surjective map
![]() $\delta _{n-1}: Y_n'\to \ Y_{n-1}'$
(see
$\delta _{n-1}: Y_n'\to \ Y_{n-1}'$
(see
![]() $(3.9))$
. Since
$(3.9))$
. Since
![]() $\triangle \Phi _n'\succ \triangle \Phi _{n-1}'$
, we have
$\triangle \Phi _n'\succ \triangle \Phi _{n-1}'$
, we have
![]() $\delta _{n-1}(y)=\triangle \Phi _{n-1}'((\triangle \Phi _n')^{-1}(y))$
for all
$\delta _{n-1}(y)=\triangle \Phi _{n-1}'((\triangle \Phi _n')^{-1}(y))$
for all
![]() $y\in Y_n'$
. Choose a countable
$y\in Y_n'$
. Choose a countable
![]() $QS$
-algebra
$QS$
-algebra
![]() $\Lambda _{n}$
on
$\Lambda _{n}$
on
![]() $Y_n'$
containing the family
$Y_n'$
containing the family
![]() $\{\lambda \circ \delta _{n-1}:\lambda \in \Lambda _{n-1}\}$
and let
$\{\lambda \circ \delta _{n-1}:\lambda \in \Lambda _{n-1}\}$
and let
![]() $\Phi _{n+1}=\Phi _n'\cup \{\lambda \circ (\triangle \Phi _n'):\lambda \in \Lambda _{n}\}$
. Next, take a countable set
$\Phi _{n+1}=\Phi _n'\cup \{\lambda \circ (\triangle \Phi _n'):\lambda \in \Lambda _{n}\}$
. Next, take a countable set
![]() $\Psi _{n+1}'\subset C(\beta X)$
containing
$\Psi _{n+1}'\subset C(\beta X)$
containing
![]() $\Psi _n$
such that for every
$\Psi _n$
such that for every
![]() $\overline {g}\in \Phi _{n+1}\cap C(\beta Y),$
there is
$\overline {g}\in \Phi _{n+1}\cap C(\beta Y),$
there is
![]() $\overline f_g\in \Psi _{n+1}'$
with
$\overline f_g\in \Psi _{n+1}'$
with
![]() $||f_g||\leq c||g||$
and
$||f_g||\leq c||g||$
and
![]() $T(f_g)=g$
. Then, by
$T(f_g)=g$
. Then, by
![]() $(3.2),$
there is countable
$(3.2),$
there is countable
![]() $\Theta _{n+1}\subset C(\beta X)$
containing
$\Theta _{n+1}\subset C(\beta X)$
containing
![]() $\Psi _{n+1}'$
with
$\Psi _{n+1}'$
with
![]() $\dim (\triangle \Theta _{n+1})(\beta X)=0$
. Finally, according to
$\dim (\triangle \Theta _{n+1})(\beta X)=0$
. Finally, according to
![]() $(3.3)$
, we extend
$(3.3)$
, we extend
![]() $\Theta _{n+1}$
to a countable admissible set
$\Theta _{n+1}$
to a countable admissible set
![]() $\Psi _{n+1}\subset C(\beta X)$
such that
$\Psi _{n+1}\subset C(\beta X)$
such that
![]() $(\triangle \Psi _{n+1})(\beta X)$
is homeomorphic to
$(\triangle \Psi _{n+1})(\beta X)$
is homeomorphic to
![]() $(\triangle \Theta _{n+1})(\beta X)$
and the
$(\triangle \Theta _{n+1})(\beta X)$
and the
![]() $QS$
-algebra
$QS$
-algebra
![]() $\mathcal A_{n+1}=\pi (\Psi _{n+1})$
on
$\mathcal A_{n+1}=\pi (\Psi _{n+1})$
on
![]() $(\triangle \Psi _{n+1})(\beta X)$
satisfies condition (2.3). This completes the induction.
$(\triangle \Psi _{n+1})(\beta X)$
satisfies condition (2.3). This completes the induction.
Let
![]() $\Psi =\bigcup _n\Psi _n$
,
$\Psi =\bigcup _n\Psi _n$
,
![]() $X_0=(\triangle \Psi )(X)$
,
$X_0=(\triangle \Psi )(X)$
,
![]() $\overline X_n=(\triangle \Psi _n)(\beta X),$
and
$\overline X_n=(\triangle \Psi _n)(\beta X),$
and
![]() $\overline X_0=(\triangle \Psi )(\beta X)$
. Similarly, let
$\overline X_0=(\triangle \Psi )(\beta X)$
. Similarly, let
![]() $\Phi =\bigcup _n\Phi _n$
,
$\Phi =\bigcup _n\Phi _n$
,
![]() $Y_0=h_0(Y),$
and
$Y_0=h_0(Y),$
and
![]() $\overline Y_0=(\triangle \Phi )(\beta Y)$
, where
$\overline Y_0=(\triangle \Phi )(\beta Y)$
, where
![]() $h_0=(\triangle \Phi )|Y$
. Both
$h_0=(\triangle \Phi )|Y$
. Both
![]() $\Psi $
and
$\Psi $
and
![]() $\Phi $
are countable and
$\Phi $
are countable and
![]() $\Psi $
is an admissible subset of
$\Psi $
is an admissible subset of
![]() $C(\beta X)$
(see
$C(\beta X)$
(see
![]() $(3.4))$
. Hence, the family
$(3.4))$
. Hence, the family
![]() $E(\overline X_0)=\{\pi _{\overline f}:\overline f\in \Psi \}$
is a countable
$E(\overline X_0)=\{\pi _{\overline f}:\overline f\in \Psi \}$
is a countable
![]() $QS$
-algebra on
$QS$
-algebra on
![]() $\overline X_0$
. Moreover, the family
$\overline X_0$
. Moreover, the family
![]() $E(Y_0)=\{\pi _{\overline g}|Y_0:\overline g\in \Phi \}$
is extendable over
$E(Y_0)=\{\pi _{\overline g}|Y_0:\overline g\in \Phi \}$
is extendable over
![]() $\overline Y_0$
. Since
$\overline Y_0$
. Since
![]() $\Psi _n\subset \Psi _{n+1}$
for every n, there are maps
$\Psi _n\subset \Psi _{n+1}$
for every n, there are maps
![]() $\theta _n^{n+1}:\overline X_{n+1}\to \overline X_n$
. Because
$\theta _n^{n+1}:\overline X_{n+1}\to \overline X_n$
. Because
![]() $\Psi =\bigcup _n\Psi _n$
, the space
$\Psi =\bigcup _n\Psi _n$
, the space
![]() $\overline X_0$
is the limit of the inverse sequence
$\overline X_0$
is the limit of the inverse sequence
![]() $S_X=\{\overline X_n,\theta _n^{n+1}\}$
with
$S_X=\{\overline X_n,\theta _n^{n+1}\}$
with
![]() $\dim \overline X_n=0$
for all n. Hence,
$\dim \overline X_n=0$
for all n. Hence,
![]() $\overline X_0$
is also zero-dimensional (see [Reference Engelking2, Theorem 3.4.11]. Observe also that
$\overline X_0$
is also zero-dimensional (see [Reference Engelking2, Theorem 3.4.11]. Observe also that
![]() $E(\overline X_0)=\bigcup _{n=1}^\infty \{h\circ \theta _n:h\in \mathcal A_n\}$
.
$E(\overline X_0)=\bigcup _{n=1}^\infty \{h\circ \theta _n:h\in \mathcal A_n\}$
.
Let us show that
![]() $E(\overline X_0)$
ia a
$E(\overline X_0)$
ia a
![]() $QS$
-algebra satisfying condition (2.3). Because
$QS$
-algebra satisfying condition (2.3). Because
![]() $E(\overline X_0)$
is the union of the increasing sequence of the families
$E(\overline X_0)$
is the union of the increasing sequence of the families
![]() $\{h\circ \theta _n:h\in \mathcal A_n\}$
and each
$\{h\circ \theta _n:h\in \mathcal A_n\}$
and each
![]() $\mathcal A_n$
is a
$\mathcal A_n$
is a
![]() $QS$
-algebra,
$QS$
-algebra,
![]() $E(\overline X_0)$
is closed under sums, multiplications, and multiplications by rational numbers. It remains to show that for every
$E(\overline X_0)$
is closed under sums, multiplications, and multiplications by rational numbers. It remains to show that for every
![]() $x\in \overline X_0$
and every its neighborhood
$x\in \overline X_0$
and every its neighborhood
![]() $U\subset \overline X_0$
, there is
$U\subset \overline X_0$
, there is
![]() $\overline f\in E(\overline X_0)$
such that
$\overline f\in E(\overline X_0)$
such that
![]() $\overline f(x)=1$
and
$\overline f(x)=1$
and
![]() $\overline f(\overline X_0\backslash U)=0$
. But that follows from the proof of the more general condition (2.3). To show that
$\overline f(\overline X_0\backslash U)=0$
. But that follows from the proof of the more general condition (2.3). To show that
![]() $E(\overline X_0)$
satisfies
$E(\overline X_0)$
satisfies
![]() $(2.3)$
, take a compact set
$(2.3)$
, take a compact set
![]() $K\subset \overline X_0$
and an open set
$K\subset \overline X_0$
and an open set
![]() $W\subset \overline X_0$
containing K. Because
$W\subset \overline X_0$
containing K. Because
![]() $\overline X_0$
is the limit of the inverse sequence
$\overline X_0$
is the limit of the inverse sequence
![]() $S_X=\{\overline X_n,\theta _n^{n+1}\}$
, there are n, a compact set
$S_X=\{\overline X_n,\theta _n^{n+1}\}$
, there are n, a compact set
![]() $K_n\subset \overline X_n$
and an open set
$K_n\subset \overline X_n$
and an open set
![]() $W_n\subset \overline X_n$
containing
$W_n\subset \overline X_n$
containing
![]() $K_n$
such that
$K_n$
such that
![]() $K\subset \theta _n^{-1}(K_n)\subset \theta _n^{-1}(W_n)\subset W$
, where
$K\subset \theta _n^{-1}(K_n)\subset \theta _n^{-1}(W_n)\subset W$
, where
![]() ${\theta _n:\overline X_0\to \overline X_n}$
denotes the n-th projection in
${\theta _n:\overline X_0\to \overline X_n}$
denotes the n-th projection in
![]() $S_X$
. Then, according to condition (3.8), there is
$S_X$
. Then, according to condition (3.8), there is
![]() $f_n\in \mathcal A_n$
with
$f_n\in \mathcal A_n$
with
![]() $f_n|K_n=1$
,
$f_n|K_n=1$
,
![]() $f_n|(\overline X_n\backslash W_n)=0$
and
$f_n|(\overline X_n\backslash W_n)=0$
and
![]() $f_n:\overline X_n\to [0,1]$
. Finally, observe that the function
$f_n:\overline X_n\to [0,1]$
. Finally, observe that the function
![]() $\overline f=f_n\circ \theta _n:\overline X_0\to [0,1]$
belongs to
$\overline f=f_n\circ \theta _n:\overline X_0\to [0,1]$
belongs to
![]() $E(\overline X_0)$
and
$E(\overline X_0)$
and
![]() $\overline f$
satisfies the conditions
$\overline f$
satisfies the conditions
![]() $\overline f|K=1$
and
$\overline f|K=1$
and
![]() $\overline f|(\overline X_0\backslash W)=0$
.
$\overline f|(\overline X_0\backslash W)=0$
.
It follows from the construction that
![]() $\Phi =\{\overline {T(f)}:\overline f\in \Psi \}$
and for every
$\Phi =\{\overline {T(f)}:\overline f\in \Psi \}$
and for every
![]() $\overline g\in \Phi \cap C(\beta Y),$
there is
$\overline g\in \Phi \cap C(\beta Y),$
there is
![]() $\overline f_g\in \Psi $
with
$\overline f_g\in \Psi $
with
![]() $T(f_g)=g$
and
$T(f_g)=g$
and
![]() $||f_g||\leq c||g||$
. Observe that for all
$||f_g||\leq c||g||$
. Observe that for all
![]() $\overline f\in \Psi $
and
$\overline f\in \Psi $
and
![]() $\overline g\in \Phi ,$
we have
$\overline g\in \Phi ,$
we have
![]() $f=\pi _{\overline f}\circ (\triangle \Psi )|X$
and
$f=\pi _{\overline f}\circ (\triangle \Psi )|X$
and
![]() $g=\pi _{\overline g}\circ (\triangle \Phi )|Y$
. Therefore, there is a surjective map
$g=\pi _{\overline g}\circ (\triangle \Phi )|Y$
. Therefore, there is a surjective map
![]() $\varphi :E_p(X_0)\to E_p(Y_0)$
defined by
$\varphi :E_p(X_0)\to E_p(Y_0)$
defined by
![]() $\varphi (\pi _f)=\pi _{T(f)}$
, where
$\varphi (\pi _f)=\pi _{T(f)}$
, where
![]() $\pi _f$
and
$\pi _f$
and
![]() $\pi _g$
denote, respectively, the functions
$\pi _g$
denote, respectively, the functions
![]() $\pi _{\overline f}|X_0$
and
$\pi _{\overline f}|X_0$
and
![]() $\pi _{\overline g}|Y_0$
. Moreover,
$\pi _{\overline g}|Y_0$
. Moreover,
![]() $||f||=||\pi _f||$
and
$||f||=||\pi _f||$
and
![]() ${||g||=||\pi _g||}$
for all
${||g||=||\pi _g||}$
for all
![]() $\overline f\in \Psi $
and
$\overline f\in \Psi $
and
![]() $\overline g\in \Phi \cap C(\beta Y)$
. This implies that
$\overline g\in \Phi \cap C(\beta Y)$
. This implies that
![]() $\varphi $
is a c-good surjection.
$\varphi $
is a c-good surjection.
Let’s show that
![]() $\varphi $
is uniformly continuous. Suppose
$\varphi $
is uniformly continuous. Suppose
is a neighborhood of the zero function in
![]() $E_p(Y_0)$
. Take points
$E_p(Y_0)$
. Take points
![]() $\overline y_i\in Y$
with
$\overline y_i\in Y$
with
![]() $h_0(\overline y_i)=y_i$
,
$h_0(\overline y_i)=y_i$
,
![]() $i=1,2,\ldots ,k$
, and let
$i=1,2,\ldots ,k$
, and let
![]() $\widetilde V=\{g\in D_p(Y):|g(\overline y_i)|<\varepsilon {~}\forall i\leq k\}$
. Since T is uniformly continuous, there is a neighborhood
$\widetilde V=\{g\in D_p(Y):|g(\overline y_i)|<\varepsilon {~}\forall i\leq k\}$
. Since T is uniformly continuous, there is a neighborhood
of the zero function in
![]() $D_p(X)$
such that
$D_p(X)$
such that
![]() $f-f'\in \widetilde U$
implies
$f-f'\in \widetilde U$
implies
![]() $T(f)-T(f')\in \widetilde V$
for all
$T(f)-T(f')\in \widetilde V$
for all
![]() $f,f'\in D_p(X)$
. Let
$f,f'\in D_p(X)$
. Let
![]() $x_j=(\triangle \Psi )(\overline x_j)$
and
$x_j=(\triangle \Psi )(\overline x_j)$
and
Obviously,
![]() $\pi _f-\pi _{f'}\in U$
implies
$\pi _f-\pi _{f'}\in U$
implies
![]() $f-f'\in \widetilde U$
. Hence,
$f-f'\in \widetilde U$
. Hence,
![]() $T(f)-T(f')\in \widetilde V$
, which yields
$T(f)-T(f')\in \widetilde V$
, which yields
![]() $\varphi (\pi _f)-\varphi (\pi _{f'})\in V$
.
$\varphi (\pi _f)-\varphi (\pi _{f'})\in V$
.
Finally, we can show that
![]() $E(\overline Y_0)$
contains a
$E(\overline Y_0)$
contains a
![]() $QS$
-algebra on
$QS$
-algebra on
![]() $\overline Y_0$
. Since
$\overline Y_0$
. Since
![]() $\Lambda _n\subset C(Y_n')$
is a
$\Lambda _n\subset C(Y_n')$
is a
![]() $QS$
-algebra on
$QS$
-algebra on
![]() $Y_n'$
, it separates the points and the closed sets in
$Y_n'$
, it separates the points and the closed sets in
![]() $Y_n'$
. So,
$Y_n'$
. So,
![]() $Y_n'$
is homeomorphic to
$Y_n'$
is homeomorphic to
![]() $(\triangle \Lambda _n)(Y_n')$
. This implies that
$(\triangle \Lambda _n)(Y_n')$
. This implies that
![]() $Y_{n+1}=(\triangle \Phi _{n+1})(\beta Y)$
is homeomorphic to
$Y_{n+1}=(\triangle \Phi _{n+1})(\beta Y)$
is homeomorphic to
![]() $Y_n'$
. Therefore,
$Y_n'$
. Therefore,
![]() $\Lambda _n$
can be considered as a
$\Lambda _n$
can be considered as a
![]() $QS$
-algebra on
$QS$
-algebra on
![]() $Y_{n+1}$
. On the other hand,
$Y_{n+1}$
. On the other hand,
![]() $\overline Y_0$
is the limit of the inverse sequence
$\overline Y_0$
is the limit of the inverse sequence
![]() $S_Y=\{Y_{n+1},\gamma _{n+1}^{n+2},n\geq 1\}$
, where
$S_Y=\{Y_{n+1},\gamma _{n+1}^{n+2},n\geq 1\}$
, where
![]() $\gamma _{n+1}^{n+2}:Y_{n+2}\to Y_{n+1}$
is the surjective map generated by the inclusion
$\gamma _{n+1}^{n+2}:Y_{n+2}\to Y_{n+1}$
is the surjective map generated by the inclusion
![]() $\Phi _{n+1}\subset \Phi _{n+2}$
. According to condition (3.9), we can also assume that
$\Phi _{n+1}\subset \Phi _{n+2}$
. According to condition (3.9), we can also assume that
![]() $\Lambda _{n+1}$
contains the family
$\Lambda _{n+1}$
contains the family
![]() $\{\lambda \circ \gamma _{n+1}^{n+2}:\lambda \in \Lambda _n\}$
. Denote by
$\{\lambda \circ \gamma _{n+1}^{n+2}:\lambda \in \Lambda _n\}$
. Denote by
![]() $\gamma _{n+1}:\overline Y_0\to Y_{n+1}$
the projections in
$\gamma _{n+1}:\overline Y_0\to Y_{n+1}$
the projections in
![]() $S_Y$
, and let
$S_Y$
, and let
![]() $\Gamma _n=\{\lambda \circ \gamma _{n+1}:\lambda \in \Lambda _n\}$
. Then,
$\Gamma _n=\{\lambda \circ \gamma _{n+1}:\lambda \in \Lambda _n\}$
. Then,
![]() $\{\Gamma _n\}_{n\geq 1}$
is an increasing sequence of countable families and
$\{\Gamma _n\}_{n\geq 1}$
is an increasing sequence of countable families and
![]() $\Gamma _n\subset E(\overline Y_0)=\{\pi _{\overline g}:\overline g\in \Phi \}$
for every n. We claim that
$\Gamma _n\subset E(\overline Y_0)=\{\pi _{\overline g}:\overline g\in \Phi \}$
for every n. We claim that
![]() $\Gamma =\bigcup _n\Gamma _n$
is a
$\Gamma =\bigcup _n\Gamma _n$
is a
![]() $QS$
-algebra on
$QS$
-algebra on
![]() $\overline Y_0$
. Indeed,
$\overline Y_0$
. Indeed,
![]() $\Gamma $
is closed under addition, multiplication, and multiplication by rational numbers. Because for every
$\Gamma $
is closed under addition, multiplication, and multiplication by rational numbers. Because for every
![]() $y\in \overline Y_0$
and its neighborhood
$y\in \overline Y_0$
and its neighborhood
![]() $V\subset \overline Y_0$
, there is n and an open set
$V\subset \overline Y_0$
, there is n and an open set
![]() $V_n\subset Y_{n+1}$
such that
$V_n\subset Y_{n+1}$
such that
![]() $y_n=\gamma _{n+1}(y)\in V_n$
and
$y_n=\gamma _{n+1}(y)\in V_n$
and
![]() $\gamma _{n+1}^{-1}(V_n)\subset V$
, there exists
$\gamma _{n+1}^{-1}(V_n)\subset V$
, there exists
![]() $\lambda \in \Lambda _n$
with
$\lambda \in \Lambda _n$
with
![]() $\lambda (y_n)=1$
and
$\lambda (y_n)=1$
and
![]() $\lambda (Y_{n+1}\backslash V_n)=0$
. Then,
$\lambda (Y_{n+1}\backslash V_n)=0$
. Then,
![]() $g=\lambda \circ \gamma _{n+1}\in \Gamma $
,
$g=\lambda \circ \gamma _{n+1}\in \Gamma $
,
![]() $g(y)=1,$
and
$g(y)=1,$
and
![]() $g(\overline Y_0\backslash V)=0$
.
$g(\overline Y_0\backslash V)=0$
.
To prove Theorem 1.1, we apply Proposition 2.1 with
![]() $H=\overline X_0$
to find a
$H=\overline X_0$
to find a
![]() $\sigma $
-compact set
$\sigma $
-compact set
![]() $Y_\infty \subset \overline Y_0$
containing
$Y_\infty \subset \overline Y_0$
containing
![]() $Y_0$
with
$Y_0$
with
![]() $\dim Y_\infty =0$
. Therefore, by [Reference Engelking2, Proposition 1.2.2],
$\dim Y_\infty =0$
. Therefore, by [Reference Engelking2, Proposition 1.2.2],
![]() $\dim Y_0=0$
.
$\dim Y_0=0$
.
Proposition 3.3 [Reference Leiderman13]
For every linear continuous surjective map
![]() $T:C_p^*(X)\to C_p^*(Y),$
there is
$T:C_p^*(X)\to C_p^*(Y),$
there is
![]() $c>0$
such that T is c-good.
$c>0$
such that T is c-good.
Proof By the Closed Graph Theorem, T considered as a map between the Banach spaces
![]() $C^*_u(X)$
and
$C^*_u(X)$
and
![]() $C^*_u(Y)$
, both equipped with the sup-norm, is continuous. Then, T induced a linear isomorphism
$C^*_u(Y)$
, both equipped with the sup-norm, is continuous. Then, T induced a linear isomorphism
![]() $T_0$
between
$T_0$
between
![]() $C^*_u(X)/K$
and
$C^*_u(X)/K$
and
![]() $C^*_u(Y)$
, where K is the kernel of T. So, for every
$C^*_u(Y)$
, where K is the kernel of T. So, for every
![]() $g\in C_u^*(Y),$
we have
$g\in C_u^*(Y),$
we have
![]() $||T_0^{-1}(g)||\leq ||T_0^{-1}||\cdot ||g||$
. Because
$||T_0^{-1}(g)||\leq ||T_0^{-1}||\cdot ||g||$
. Because
where
![]() $f\in C_u^*(X)$
with
$f\in C_u^*(X)$
with
![]() $T(f)=g$
, there exists
$T(f)=g$
, there exists
![]() $h_g\in K$
such that
$h_g\in K$
such that
![]() $||f-h_g||\leq 2||T_0^{-1}(g)||$
. Hence,
$||f-h_g||\leq 2||T_0^{-1}(g)||$
. Hence,
![]() $||f-h_g||\leq 2||T_0^{-1}||\cdot ||g||$
. Since
$||f-h_g||\leq 2||T_0^{-1}||\cdot ||g||$
. Since
![]() $T(f-h_g)=T(f)=g$
, we obtain that T is c-good with
$T(f-h_g)=T(f)=g$
, we obtain that T is c-good with
![]() $c=2||T_0^{-1}||$
.
$c=2||T_0^{-1}||$
.
Proof of Theorem 1.3
Following the proof of Theorem 1.1, we construct two sequences
![]() $\{\Psi _n\}_{n\geq 1}\subset C(\beta X)$
and
$\{\Psi _n\}_{n\geq 1}\subset C(\beta X)$
and
![]() $\{\Phi _n\}_{n\geq 1}\subset C(\beta Y,\overline {\mathbb R})$
of countable sets and countable
$\{\Phi _n\}_{n\geq 1}\subset C(\beta Y,\overline {\mathbb R})$
of countable sets and countable
![]() $QS$
-algebras
$QS$
-algebras
![]() $\mathcal A_n$
on
$\mathcal A_n$
on
![]() $\triangle \Psi _n(\beta X)$
and
$\triangle \Psi _n(\beta X)$
and
![]() $\Lambda _{n}$
on
$\Lambda _{n}$
on
![]() $Y_n'=(\triangle \Phi _n')(\beta Y)$
satisfying the conditions (3.5)–(3.10) except
$Y_n'=(\triangle \Phi _n')(\beta Y)$
satisfying the conditions (3.5)–(3.10) except
![]() $(3.7)$
. Because X and Y are separable metrizable spaces, we can choose countable sets
$(3.7)$
. Because X and Y are separable metrizable spaces, we can choose countable sets
![]() $\Psi _1$
and
$\Psi _1$
and
![]() $\Phi _1$
such that
$\Phi _1$
such that
![]() $(\triangle \Phi _1)|Y$
and
$(\triangle \Phi _1)|Y$
and
![]() $(\triangle \Psi _1)|X$
are homeomorphisms.
$(\triangle \Psi _1)|X$
are homeomorphisms.
Then, following the notations from the proof of Theorem 1.1, we have that
![]() $X_0$
and
$X_0$
and
![]() $Y_0$
are homeomorphic to X and Y, respectively. Moreover, there exists a uniformly continuous c-good surjection
$Y_0$
are homeomorphic to X and Y, respectively. Moreover, there exists a uniformly continuous c-good surjection
![]() $\varphi : E_p(X_0)\to E_p(Y_0)$
such that
$\varphi : E_p(X_0)\to E_p(Y_0)$
such that
![]() $E(\overline X_0)$
is a
$E(\overline X_0)$
is a
![]() $QS$
-algebra on
$QS$
-algebra on
![]() $\overline X_0$
satisfying condition (2.3),
$\overline X_0$
satisfying condition (2.3),
![]() $E(\overline Y_0)\subset C(\overline Y_0,\overline {\mathbb R})$
and
$E(\overline Y_0)\subset C(\overline Y_0,\overline {\mathbb R})$
and
![]() $E(\overline Y_0)$
contains a countable
$E(\overline Y_0)$
contains a countable
![]() $QS$
-algebra
$QS$
-algebra
![]() $\Gamma $
on
$\Gamma $
on
![]() $\overline Y_0$
. According to the proof of Proposition 2.1 with
$\overline Y_0$
. According to the proof of Proposition 2.1 with
![]() $H=X_0$
, there is a
$H=X_0$
, there is a
![]() $\sigma $
-compact set
$\sigma $
-compact set
![]() $Y_\infty \subset \overline Y_0$
containing
$Y_\infty \subset \overline Y_0$
containing
![]() $Y_0$
which a countable union of closed sets
$Y_0$
which a countable union of closed sets
![]() $F\subset Y_\infty $
such that F admits a map with finite fibers into a finite power of
$F\subset Y_\infty $
such that F admits a map with finite fibers into a finite power of
![]() $X_0$
. Let
$X_0$
. Let
![]() $Y_0=\bigcup _m Y_m$
with each
$Y_0=\bigcup _m Y_m$
with each
![]() $Y_m$
being compact. Then,
$Y_m$
being compact. Then,
![]() $Y_0$
can also be represented as a countable union of compact sets each admitting a map with finite powers into a finite power of
$Y_0$
can also be represented as a countable union of compact sets each admitting a map with finite powers into a finite power of
![]() $X_0$
. Now, we apply the following fact which was actually used in the proof of Proposition 2.1: Assume all powers of a
$X_0$
. Now, we apply the following fact which was actually used in the proof of Proposition 2.1: Assume all powers of a
![]() $\sigma $
-compact metrizable space P have a property
$\sigma $
-compact metrizable space P have a property
![]() $\mathcal P$
satisfying conditions (a)–(c). If a metrizable space Z is the union of countably many compact sets
$\mathcal P$
satisfying conditions (a)–(c). If a metrizable space Z is the union of countably many compact sets
![]() $Z_n$
such that each
$Z_n$
such that each
![]() $Z_n$
admits a map with finite fibers into a finite power
$Z_n$
admits a map with finite fibers into a finite power
![]() $P^{k_n}$
, then all finite powers of Z also have the property
$P^{k_n}$
, then all finite powers of Z also have the property
![]() $\mathcal P$
. Since all finite powers of
$\mathcal P$
. Since all finite powers of
![]() $X_0$
have the property
$X_0$
have the property
![]() $\mathcal P$
, where
$\mathcal P$
, where
![]() $\mathcal P$
is either weakly infinite-dimensionality or the
$\mathcal P$
is either weakly infinite-dimensionality or the
![]() $(m-C)$
-space property, by mentioned above fact, all finite powers of
$(m-C)$
-space property, by mentioned above fact, all finite powers of
![]() $Y_0$
are either weakly infinite-dimensional or have the
$Y_0$
are either weakly infinite-dimensional or have the
![]() $(m-C)$
-space property.
$(m-C)$
-space property.
4 Proof of Theorem 1.4
We consider topological properties
![]() $\mathcal P$
of separable metrizable spaces satisfying condition
$\mathcal P$
of separable metrizable spaces satisfying condition
![]() $(b)$
from the introduction section plus the following three:
$(b)$
from the introduction section plus the following three:
-
(a′) if
 $X\in \mathcal P$
, then
$X\in \mathcal P$
, then
 $F\in \mathcal P$
for every subset
$F\in \mathcal P$
for every subset
 $F\subset X$
;
$F\subset X$
; -
(c′) if
 $f:X\to Y$
is a perfect map between metrizable spaces with zero-dimensional fibers and
$f:X\to Y$
is a perfect map between metrizable spaces with zero-dimensional fibers and
 $Y\in \mathcal P$
, then
$Y\in \mathcal P$
, then
 $X\in \mathcal P$
;
$X\in \mathcal P$
; -
(d′)
 $\mathcal P$
is closed under finite products.
$\mathcal P$
is closed under finite products.
The zero-dimensionality, the countable-dimensionality, and the strong countable dimensionality satisfy these conditions (see [Reference Engelking2]).
If
![]() $E(X)\subset C(X)$
is a
$E(X)\subset C(X)$
is a
![]() $QS$
-algebra on X, then the family
$QS$
-algebra on X, then the family
![]() $LE(X)$
of all finite linear combinations
$LE(X)$
of all finite linear combinations
![]() $\sum _{i=1}^k\lambda _i\cdot f_i$
with
$\sum _{i=1}^k\lambda _i\cdot f_i$
with
![]() $f_i\in E(X)$
and
$f_i\in E(X)$
and
![]() $\lambda _i\in \mathbb R$
is called the linear hull of
$\lambda _i\in \mathbb R$
is called the linear hull of
![]() $E(X)$
.
$E(X)$
.
Proposition 4.1 Let X and Y be separable metrizable spaces and
![]() $E(X)\subset C(X)$
be a countable
$E(X)\subset C(X)$
be a countable
![]() $QS$
-algebra on X and
$QS$
-algebra on X and
![]() $E(Y)\subset C(Y)$
be a countable family. Suppose there are metrizable compactifications
$E(Y)\subset C(Y)$
be a countable family. Suppose there are metrizable compactifications
![]() $\overline X$
and
$\overline X$
and
![]() $\overline Y$
of X and Y and a countable base
$\overline Y$
of X and Y and a countable base
![]() $\mathcal B$
of
$\mathcal B$
of
![]() $\overline X$
such that:
$\overline X$
such that:
-
• every
 $f\in E(X)$
can be extended to a map
$f\in E(X)$
can be extended to a map
 $\overline f:\overline X\to \overline {\mathbb R}$
and for every finite open cover
$\overline f:\overline X\to \overline {\mathbb R}$
and for every finite open cover
 $\gamma =\{U_i:i=1,2,\ldots ,k\}$
of
$\gamma =\{U_i:i=1,2,\ldots ,k\}$
of
 $\overline X$
with elements from
$\overline X$
with elements from
 $\mathcal B,$
there exists a partition of unity
$\mathcal B,$
there exists a partition of unity
 $\{\overline f_i:i=1,2,\ldots ,k\}$
subordinated to
$\{\overline f_i:i=1,2,\ldots ,k\}$
subordinated to
 $\gamma $
with
$\gamma $
with
 $f_i\in E(X)$
;
$f_i\in E(X)$
; -
• every
 $g\in E(Y)$
can be extended to a map
$g\in E(Y)$
can be extended to a map
 $\overline g:\overline Y\to \overline {\mathbb R}$
and the set of all real-valued elements of
$\overline g:\overline Y\to \overline {\mathbb R}$
and the set of all real-valued elements of
 $E_p(\overline Y)=\{\overline g:g\in E(Y)\}$
is dense in
$E_p(\overline Y)=\{\overline g:g\in E(Y)\}$
is dense in
 $C_p(\overline Y)$
;
$C_p(\overline Y)$
; -
• for every compact set
 $K\subset \overline X$
and every open set
$K\subset \overline X$
and every open set
 $W\subset \overline X$
containing
$W\subset \overline X$
containing
 $K,$
there is
$K,$
there is
 ${f\in E(X)}$
such that
${f\in E(X)}$
such that
 $\overline f(K)=1$
,
$\overline f(K)=1$
,
 $\overline f(\overline X\backslash W)=0,$
and
$\overline f(\overline X\backslash W)=0,$
and
 $f(x)\in [0,1]$
for all
$f(x)\in [0,1]$
for all
 $x\in X$
.
$x\in X$
.
If
![]() $\overline X$
has a property
$\overline X$
has a property
![]() $\mathcal P$
satisfying conditions
$\mathcal P$
satisfying conditions
![]() $(a'),(b)$
,
$(a'),(b)$
,
![]() $(c'),$
and
$(c'),$
and
![]() $(d')$
, and
$(d')$
, and
![]() $\varphi : E_p(X)\to E_p(Y)$
is a linear continuous surjection such that
$\varphi : E_p(X)\to E_p(Y)$
is a linear continuous surjection such that
![]() $\varphi $
can be continuously extended over
$\varphi $
can be continuously extended over
![]() $LE_p(X)$
, then
$LE_p(X)$
, then
![]() $Y\in \mathcal P$
.
$Y\in \mathcal P$
.
Proof Let
![]() $E(\overline X)=\{\overline f:f\in E(X)\}$
. Every
$E(\overline X)=\{\overline f:f\in E(X)\}$
. Every
![]() $y\in \overline Y$
generates a map
$y\in \overline Y$
generates a map
![]() $l_y:E(\overline X)\to \overline {\mathbb R}$
,
$l_y:E(\overline X)\to \overline {\mathbb R}$
,
![]() $l_y(\overline f)=\overline {\varphi (f)}(y)$
. Assuming the equalities from
$l_y(\overline f)=\overline {\varphi (f)}(y)$
. Assuming the equalities from
![]() $(2.4)$
, for any
$(2.4)$
, for any
![]() $\overline f_1,\overline f_2\in E(\overline X)$
and
$\overline f_1,\overline f_2\in E(\overline X)$
and
![]() $x\in \overline X$
, we can write
$x\in \overline X$
, we can write
![]() $\overline f_1(x)+\overline f_2(x)$
but not always
$\overline f_1(x)+\overline f_2(x)$
but not always
![]() $\overline f_1+\overline f_2=\overline {f_1+f_2}$
. Also, if
$\overline f_1+\overline f_2=\overline {f_1+f_2}$
. Also, if
![]() $\overline f_1+\overline f_2\in E(\overline X)$
, it is possible that
$\overline f_1+\overline f_2\in E(\overline X)$
, it is possible that
![]() $l_y(\overline f_1+\overline f_2)\neq l_y(\overline f_1)+l_y(\overline f_2)$
. If
$l_y(\overline f_1+\overline f_2)\neq l_y(\overline f_1)+l_y(\overline f_2)$
. If
![]() $\lambda \in \mathbb R\backslash \{0\}$
and
$\lambda \in \mathbb R\backslash \{0\}$
and
![]() $\overline {\lambda \cdot f}\in E(\overline X)$
, then
$\overline {\lambda \cdot f}\in E(\overline X)$
, then
![]() $l_y(\overline {\lambda \cdot f})=\lambda \cdot l_y(\overline f)$
(here,
$l_y(\overline {\lambda \cdot f})=\lambda \cdot l_y(\overline f)$
(here,
![]() $\lambda \cdot (\pm \infty )=\pm \infty $
if
$\lambda \cdot (\pm \infty )=\pm \infty $
if
![]() $\lambda>0$
and
$\lambda>0$
and
![]() $\lambda \cdot (\pm \infty )=\mp \infty $
if
$\lambda \cdot (\pm \infty )=\mp \infty $
if
![]() $\lambda <0$
). In case
$\lambda <0$
). In case
![]() $\lambda =0$
, we have
$\lambda =0$
, we have
![]() $l_y(\overline {0\cdot f})=0$
. More general, if
$l_y(\overline {0\cdot f})=0$
. More general, if
![]() $\overline h\in C(\overline X)$
such that
$\overline h\in C(\overline X)$
such that
![]() $h\cdot f\in E(X)$
for some
$h\cdot f\in E(X)$
for some
![]() $f\in E(X)$
, then
$f\in E(X)$
, then
![]() $l_y(\overline {h\cdot f})$
is well defined.
$l_y(\overline {h\cdot f})$
is well defined.
The support of
![]() $l_y$
,
$l_y$
,
![]() $y\in \overline Y$
, is defined to be the set
$y\in \overline Y$
, is defined to be the set
![]() $supp(l_y)$
of all
$supp(l_y)$
of all
![]() $x\in \overline X$
satisfying the following condition [Reference Valov and Vuma22]: for every neighborhood
$x\in \overline X$
satisfying the following condition [Reference Valov and Vuma22]: for every neighborhood
![]() $U\subset \overline X$
of
$U\subset \overline X$
of
![]() $x,$
there is
$x,$
there is
![]() $f\in E(X)$
such that
$f\in E(X)$
such that
![]() $\overline f(\overline X\backslash U)=0$
and
$\overline f(\overline X\backslash U)=0$
and
![]() $l_y(\overline f)\neq 0$
. Obviously,
$l_y(\overline f)\neq 0$
. Obviously,
![]() $supp(l_y)$
is closed in
$supp(l_y)$
is closed in
![]() $\overline X$
.
$\overline X$
.
Claim 9
![]() $supp(l_y)$
is non-empty for all
$supp(l_y)$
is non-empty for all
![]() $y\in \overline Y$
.
$y\in \overline Y$
.
Indeed, because the set of real-valued functions from
![]() $E(\overline Y)$
is dense in
$E(\overline Y)$
is dense in
![]() $C_p(\overline Y)$
, for every
$C_p(\overline Y)$
, for every
![]() $y\in \overline Y,$
there is
$y\in \overline Y,$
there is
![]() $g\in E(\overline Y)$
with
$g\in E(\overline Y)$
with
![]() $g(y)\neq 0$
. Then, take
$g(y)\neq 0$
. Then, take
![]() $f_y\in E(X)$
such that
$f_y\in E(X)$
such that
![]() $\varphi (f_y)=g|Y$
, so
$\varphi (f_y)=g|Y$
, so
![]() $l_y(\overline f_y)=g(y)$
. If
$l_y(\overline f_y)=g(y)$
. If
![]() $supp(l_y)=\varnothing $
, every
$supp(l_y)=\varnothing $
, every
![]() $x\in \overline X$
has a neighborhood
$x\in \overline X$
has a neighborhood
![]() $V_x$
such that
$V_x$
such that
![]() $l_y(\overline f)=0$
for any
$l_y(\overline f)=0$
for any
![]() $f\in E(X)$
with
$f\in E(X)$
with
![]() $\overline f(\overline X\backslash V_x)=0$
. Passing to smaller neighborhoods, we can assume that
$\overline f(\overline X\backslash V_x)=0$
. Passing to smaller neighborhoods, we can assume that
![]() $V_x\in \mathcal B$
for all x. Hence, there is a finite open cover
$V_x\in \mathcal B$
for all x. Hence, there is a finite open cover
![]() $\gamma =\{V_{x_1},\ldots ,V_{x_k}\}$
of
$\gamma =\{V_{x_1},\ldots ,V_{x_k}\}$
of
![]() $\overline X$
and a partition of unity
$\overline X$
and a partition of unity
![]() $\mu =\{\overline h_1,\ldots ,\overline h_k\}\subset E(\overline X)$
subordinated to
$\mu =\{\overline h_1,\ldots ,\overline h_k\}\subset E(\overline X)$
subordinated to
![]() $\gamma $
. Then,
$\gamma $
. Then,
![]() $f_y\cdot h_i\in E(X)$
and
$f_y\cdot h_i\in E(X)$
and
![]() $\overline {f_y\cdot h_i}|(\overline X\backslash V_{x_i})=0,$
which implies
$\overline {f_y\cdot h_i}|(\overline X\backslash V_{x_i})=0,$
which implies
![]() $l_y(\overline {f_y\cdot h_i})=0$
for all i. Because
$l_y(\overline {f_y\cdot h_i})=0$
for all i. Because
![]() $\mu $
is a partition of unity,
$\mu $
is a partition of unity,
![]() $\overline f_y=\sum _{i=1}^k\overline {f_y\cdot h_i}$
. So,
$\overline f_y=\sum _{i=1}^k\overline {f_y\cdot h_i}$
. So,
![]() $l_y(\overline f_y)=\sum _{i=1}^kl_y(\overline {f_y\cdot h_i})=0$
, a contradiction.
$l_y(\overline f_y)=\sum _{i=1}^kl_y(\overline {f_y\cdot h_i})=0$
, a contradiction.
Claim 10 Let
![]() $U\subset \overline X$
be a neighborhood of
$U\subset \overline X$
be a neighborhood of
![]() $supp(l_y)$
and
$supp(l_y)$
and
![]() $f,g\in E(X)$
with
$f,g\in E(X)$
with
![]() $\overline f|U=\overline g|U$
. Then,
$\overline f|U=\overline g|U$
. Then,
![]() $l_y(\overline f)=l_y(\overline g)$
. In particular,
$l_y(\overline f)=l_y(\overline g)$
. In particular,
![]() $\overline f(U)=0$
implies
$\overline f(U)=0$
implies
![]() $l_y(\overline f)=0$
.
$l_y(\overline f)=0$
.
First, let
![]() $\overline f(U)=0$
for some
$\overline f(U)=0$
for some
![]() $\overline f\in E(\overline X)$
. We can assume that U is a finite union of open sets
$\overline f\in E(\overline X)$
. We can assume that U is a finite union of open sets
![]() $V_i$
from
$V_i$
from
![]() $\mathcal B$
,
$\mathcal B$
,
![]() $i=1,\ldots ,k$
. Every
$i=1,\ldots ,k$
. Every
![]() $x\in \overline X\backslash U$
has a neighborhood
$x\in \overline X\backslash U$
has a neighborhood
![]() $V_x$
such that
$V_x$
such that
![]() $l_y(\overline g)=0$
for any
$l_y(\overline g)=0$
for any
![]() $g\in E(X)$
with
$g\in E(X)$
with
![]() $\overline g(\overline X\backslash V_x)=0$
. As in the proof of Claim 9, we can assume that
$\overline g(\overline X\backslash V_x)=0$
. As in the proof of Claim 9, we can assume that
![]() $V_x\in \mathcal B$
, and choose another neighborhood
$V_x\in \mathcal B$
, and choose another neighborhood
![]() $U_x\in \mathcal B$
with
$U_x\in \mathcal B$
with
![]() $\overline U_x\subset V_x$
. Take a finite open cover
$\overline U_x\subset V_x$
. Take a finite open cover
![]() $\{U_{x_1},\ldots ,U_{x_m}\}$
of
$\{U_{x_1},\ldots ,U_{x_m}\}$
of
![]() $\overline X\backslash U$
. Then,
$\overline X\backslash U$
. Then,
![]() $\gamma =\{V_1,\ldots ,V_k,U_{x_1},\ldots ,U_{x_m}\}$
is an open cover of
$\gamma =\{V_1,\ldots ,V_k,U_{x_1},\ldots ,U_{x_m}\}$
is an open cover of
![]() $\overline X$
consisting of elements from
$\overline X$
consisting of elements from
![]() $\mathcal B$
. Hence, there exits a partition of unity
$\mathcal B$
. Hence, there exits a partition of unity
![]() $\{\overline h_1,\ldots ,\overline h_k,\overline \theta _1,\ldots ,\overline \theta _m\}\subset E(\overline X)$
subordinated to
$\{\overline h_1,\ldots ,\overline h_k,\overline \theta _1,\ldots ,\overline \theta _m\}\subset E(\overline X)$
subordinated to
![]() $\gamma $
. Then,
$\gamma $
. Then,
![]() $h_i\cdot f, \theta _j\cdot f\in E(X)$
for all
$h_i\cdot f, \theta _j\cdot f\in E(X)$
for all
![]() $i,j$
and
$i,j$
and
![]() $f=\sum _{i=1}^kh_i\cdot f+\sum _{j=1}^m\theta _j\cdot f$
. Take a sequence
$f=\sum _{i=1}^kh_i\cdot f+\sum _{j=1}^m\theta _j\cdot f$
. Take a sequence
![]() $\{y_n\}\subset Y$
with
$\{y_n\}\subset Y$
with
![]() $\lim _n y_n=y$
. So,
$\lim _n y_n=y$
. So,
![]() $\varphi (f)(y_n)=\sum _{i=1}^k\varphi (h_i\cdot f)(y_n)+\sum _{j=1}^m\varphi (\theta _j\cdot f)(y_n)$
. Observe that
$\varphi (f)(y_n)=\sum _{i=1}^k\varphi (h_i\cdot f)(y_n)+\sum _{j=1}^m\varphi (\theta _j\cdot f)(y_n)$
. Observe that
![]() $(h_i\cdot f)(x)=0$
for all
$(h_i\cdot f)(x)=0$
for all
![]() $x\in X$
, so
$x\in X$
, so
![]() $\varphi (h_i\cdot f)$
is the zero function on Y and
$\varphi (h_i\cdot f)$
is the zero function on Y and
![]() $\varphi (h_i\cdot f)(y_n)=0$
,
$\varphi (h_i\cdot f)(y_n)=0$
,
![]() $i=1,\ldots ,k$
. Hence,
$i=1,\ldots ,k$
. Hence,
![]() $\varphi (f)(y_n)=\sum _{j=1}^m\varphi (\theta _j\cdot f)(y_n)$
. On the other hand,
$\varphi (f)(y_n)=\sum _{j=1}^m\varphi (\theta _j\cdot f)(y_n)$
. On the other hand,
![]() $(\theta _j\cdot f)(x)=0$
for all
$(\theta _j\cdot f)(x)=0$
for all
![]() $x\in X\backslash U_{x_j}$
. So,
$x\in X\backslash U_{x_j}$
. So,
![]() $(\overline {\theta _j\cdot f})(x)=0$
for all
$(\overline {\theta _j\cdot f})(x)=0$
for all
![]() $x\in \overline X\backslash V_{x_j}$
because
$x\in \overline X\backslash V_{x_j}$
because
![]() $\overline X\backslash V_{x_j}\subset \overline {X\backslash U_{x_j}}$
. This implies that
$\overline X\backslash V_{x_j}\subset \overline {X\backslash U_{x_j}}$
. This implies that
![]() $l_y(\overline {\theta _j\cdot f})=0$
for all
$l_y(\overline {\theta _j\cdot f})=0$
for all
![]() $j=1,\ldots ,m$
. Since,
$j=1,\ldots ,m$
. Since,
![]() ${l_y(\overline {\theta _j\cdot f})=\lim _n\varphi (\theta _j\cdot f)(y_n)=0}$
, we have
${l_y(\overline {\theta _j\cdot f})=\lim _n\varphi (\theta _j\cdot f)(y_n)=0}$
, we have
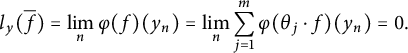 $$ \begin{align*}l_y(\overline f)=\lim_n\varphi(f)(y_n)=\lim_n\sum_{j=1}^m\varphi(\theta_j\cdot f)(y_n)=0.\end{align*} $$
$$ \begin{align*}l_y(\overline f)=\lim_n\varphi(f)(y_n)=\lim_n\sum_{j=1}^m\varphi(\theta_j\cdot f)(y_n)=0.\end{align*} $$
Suppose now that
![]() $\overline f|U=\overline g|U$
for some
$\overline f|U=\overline g|U$
for some
![]() $f,g\in E(X)$
. Then,
$f,g\in E(X)$
. Then,
![]() $f(x)-g(x)=0$
for all
$f(x)-g(x)=0$
for all
![]() $x\in U\cap X$
. Consequently,
$x\in U\cap X$
. Consequently,
![]() $(\overline {f-g})(x)=0$
for all
$(\overline {f-g})(x)=0$
for all
![]() $x\in U$
and, according to the previous paragraph,
$x\in U$
and, according to the previous paragraph,
![]() $l_y(\overline {f-g})=0$
. Hence, for every sequence
$l_y(\overline {f-g})=0$
. Hence, for every sequence
![]() $\{y_n\}\subset Y$
converging to
$\{y_n\}\subset Y$
converging to
![]() $y,$
we have
$y,$
we have
Claim 11 If
![]() $supp(l_{y_0})\cap U\neq \varnothing $
for some open
$supp(l_{y_0})\cap U\neq \varnothing $
for some open
![]() $U\subset \overline X$
and
$U\subset \overline X$
and
![]() $y_0\in \overline Y$
, then
$y_0\in \overline Y$
, then
![]() $y_0$
has a neighborhood
$y_0$
has a neighborhood
![]() $V\subset \overline Y$
such that
$V\subset \overline Y$
such that
![]() $supp(l_{y})\cap U\neq \varnothing $
for every
$supp(l_{y})\cap U\neq \varnothing $
for every
![]() $y\in V$
.
$y\in V$
.
Let
![]() $x_0\in supp(l_{y_0})\cap U$
and
$x_0\in supp(l_{y_0})\cap U$
and
![]() $\overline f\in E(\overline X)$
be such that
$\overline f\in E(\overline X)$
be such that
![]() $\overline f(\overline X\backslash W)=0$
and
$\overline f(\overline X\backslash W)=0$
and
![]() $l_{y_0}(\overline f)\neq 0$
, where W is a neighborhood of
$l_{y_0}(\overline f)\neq 0$
, where W is a neighborhood of
![]() $x_0$
with
$x_0$
with
![]() $\overline W\subset U$
. Assuming the claim is not true, we can find a sequence
$\overline W\subset U$
. Assuming the claim is not true, we can find a sequence
![]() $\{y_n\}\subset \overline Y$
converging to
$\{y_n\}\subset \overline Y$
converging to
![]() $y_0$
such that
$y_0$
such that
![]() $supp(l_{y_n})\cap U=\varnothing $
for every n. Since
$supp(l_{y_n})\cap U=\varnothing $
for every n. Since
![]() $\overline X\backslash \overline W$
is a neighborhood of each
$\overline X\backslash \overline W$
is a neighborhood of each
![]() $supp(l_{y_n})$
, by Claim 10,
$supp(l_{y_n})$
, by Claim 10,
![]() $l_{y_n}(\overline f)=0$
. Because
$l_{y_n}(\overline f)=0$
. Because
![]() $\lim _n l_{y_n}(\overline f)=l_{y_0}(\overline f)$
, we have
$\lim _n l_{y_n}(\overline f)=l_{y_0}(\overline f)$
, we have
![]() $l_{y_0}(\overline f)=0$
, a contradiction.
$l_{y_0}(\overline f)=0$
, a contradiction.
Following the notations from the proof of Proposition 2.1, for every
![]() $y\in \overline Y,$
we define
$y\in \overline Y,$
we define
Claim 12 If
![]() $y\in Y$
then
$y\in Y$
then
![]() $supp(l_{y})=\{x_1(y),x_2(y),\ldots ,x_q(y)\}$
is a finite non-empty subset of X. Moreover, there exist real numbers
$supp(l_{y})=\{x_1(y),x_2(y),\ldots ,x_q(y)\}$
is a finite non-empty subset of X. Moreover, there exist real numbers
![]() $\lambda _i(y)$
,
$\lambda _i(y)$
,
![]() $i=1,\ldots ,q$
, such that
$i=1,\ldots ,q$
, such that
![]() $\sum _{i=1}^q|\lambda _i(y)|=a(y)$
and
$\sum _{i=1}^q|\lambda _i(y)|=a(y)$
and
![]() $l_y(\overline f)=\sum _{i=1}^q\lambda _i(y)\overline f(x_i(y))$
for all
$l_y(\overline f)=\sum _{i=1}^q\lambda _i(y)\overline f(x_i(y))$
for all
![]() $\overline f\in E(\overline X)$
.
$\overline f\in E(\overline X)$
.
Let
![]() $\widetilde \varphi :LE_p(X)\to LE_p(Y)$
be the continuous extension of
$\widetilde \varphi :LE_p(X)\to LE_p(Y)$
be the continuous extension of
![]() $\varphi $
. Then, every
$\varphi $
. Then, every
![]() $l_y$
,
$l_y$
,
![]() $y\in Y$
, can be continuously extended to a linear functional
$y\in Y$
, can be continuously extended to a linear functional
![]() $\widetilde l_y:LE_p(X)\to \mathbb R$
,
$\widetilde l_y:LE_p(X)\to \mathbb R$
,
![]() $\widetilde l_y(\sum _{i=1}^k\lambda _i\cdot f_i)=\sum _{i=1}^k\lambda _i\cdot l_y(f_i)$
. Since
$\widetilde l_y(\sum _{i=1}^k\lambda _i\cdot f_i)=\sum _{i=1}^k\lambda _i\cdot l_y(f_i)$
. Since
![]() $\widetilde \varphi $
is uniformly continuous, according to the proof of Claim 1 from Proposition 2.1, for every
$\widetilde \varphi $
is uniformly continuous, according to the proof of Claim 1 from Proposition 2.1, for every
![]() $y\in Y,$
there exists a finite set
$y\in Y,$
there exists a finite set
![]() $K=\{x_1(y),x_2(y),\ldots ,x_q(y)\}\subset X$
such that
$K=\{x_1(y),x_2(y),\ldots ,x_q(y)\}\subset X$
such that
Because
![]() $\widetilde l_y$
is linear, we can show that
$\widetilde l_y$
is linear, we can show that
![]() $\widetilde l_y(g)=0$
for any
$\widetilde l_y(g)=0$
for any
![]() $g\in LE(X)$
with
$g\in LE(X)$
with
![]() $g(x_i(y))=0$
,
$g(x_i(y))=0$
,
![]() $i=1,\ldots ,q$
. Since
$i=1,\ldots ,q$
. Since
![]() $E(X)$
is a
$E(X)$
is a
![]() $QS$
-algebra, for every
$QS$
-algebra, for every
![]() $i,$
there is a function
$i,$
there is a function
![]() $g_i\in E(X)$
such that
$g_i\in E(X)$
such that
![]() $g_i(x_i(y))=1$
and
$g_i(x_i(y))=1$
and
![]() $g_i(x_j(y))=0$
with
$g_i(x_j(y))=0$
with
![]() $j\neq i$
. Now, for every
$j\neq i$
. Now, for every
![]() $f\in E(X),$
the function
$f\in E(X),$
the function
![]() $g=f-\sum _{i=1}^qg_i\cdot f(x_i(y))$
belongs to
$g=f-\sum _{i=1}^qg_i\cdot f(x_i(y))$
belongs to
![]() $LE(X)$
and
$LE(X)$
and
![]() $g(x_i(y))=0$
for all i. So,
$g(x_i(y))=0$
for all i. So,
![]() $\widetilde l_y(g)=0$
and
$\widetilde l_y(g)=0$
and
![]() $l_y(f)=\sum _{i=1}^q\lambda _i(y)f(x_i(y))$
, where
$l_y(f)=\sum _{i=1}^q\lambda _i(y)f(x_i(y))$
, where
![]() $\lambda _i(y)=l_y(g_i)$
. Because
$\lambda _i(y)=l_y(g_i)$
. Because
![]() $y\in Y$
, we can also write
$y\in Y$
, we can also write
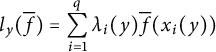 $$ \begin{align*}l_y(\overline f)=\sum_{i=1}^q\lambda_i(y)\overline f(x_i(y))\end{align*} $$
$$ \begin{align*}l_y(\overline f)=\sum_{i=1}^q\lambda_i(y)\overline f(x_i(y))\end{align*} $$
with
![]() $\lambda _i(y)=l_y(\overline g_i)$
. Note that each
$\lambda _i(y)=l_y(\overline g_i)$
. Note that each
![]() $\lambda _i(y)$
is a real number because
$\lambda _i(y)$
is a real number because
![]() $l_y(g_i)=\varphi (g_i)(y)$
. The last equality is valid for all
$l_y(g_i)=\varphi (g_i)(y)$
. The last equality is valid for all
![]() $\overline f\in E(\overline X)$
and shows that
$\overline f\in E(\overline X)$
and shows that
![]() $supp(l_y)=\{x_i(y):\lambda _i(y)\neq 0\}\subset K$
. Note that, by Claim 9,
$supp(l_y)=\{x_i(y):\lambda _i(y)\neq 0\}\subset K$
. Note that, by Claim 9,
![]() $supp(l_y)\neq \varnothing $
.
$supp(l_y)\neq \varnothing $
.
To complete the proof of Claim 12, assume that
![]() $supp(l_y)=K$
, and for every natural k take a function
$supp(l_y)=K$
, and for every natural k take a function
![]() $f_k\in E(X)$
with
$f_k\in E(X)$
with
![]() $f_k(x_i(y))=\varepsilon _i(1-1/k)$
, where
$f_k(x_i(y))=\varepsilon _i(1-1/k)$
, where
![]() $\varepsilon _i=1$
if
$\varepsilon _i=1$
if
![]() $\lambda _i(y)>0$
and
$\lambda _i(y)>0$
and
![]() $\varepsilon _i=-1$
if
$\varepsilon _i=-1$
if
![]() $\lambda _i(y)<0$
. Clearly,
$\lambda _i(y)<0$
. Clearly,
![]() $|f_k(x_i(y))|<1$
for all
$|f_k(x_i(y))|<1$
for all
![]() $i,k$
and
$i,k$
and
![]() $\lim _kl_y(\overline f_k)=\sum _{i=1}^q|\lambda _i(y)|$
. Hence,
$\lim _kl_y(\overline f_k)=\sum _{i=1}^q|\lambda _i(y)|$
. Hence,
![]() $\sum _{i=1}^q|\lambda _i(y)|\leq a(y)$
. The reverse inequality
$\sum _{i=1}^q|\lambda _i(y)|\leq a(y)$
. The reverse inequality
![]() $a(y)\leq \sum _{i=1}^q|\lambda _i(y)|$
follows from
$a(y)\leq \sum _{i=1}^q|\lambda _i(y)|$
follows from
![]() $l_y(\overline f)=\sum _{i=1}^q\lambda _i(y)\overline f(x_i(y))$
,
$l_y(\overline f)=\sum _{i=1}^q\lambda _i(y)\overline f(x_i(y))$
,
![]() $\overline f\in E(\overline X)$
.
$\overline f\in E(\overline X)$
.
For every
![]() $p,q\in \mathbb N,$
let
$p,q\in \mathbb N,$
let
![]() $Y_{p,q}=\{y\in \overline Y:|supp(l_y)|\leq q{~}\mbox {and}{~}a(y)\leq p\}$
.
$Y_{p,q}=\{y\in \overline Y:|supp(l_y)|\leq q{~}\mbox {and}{~}a(y)\leq p\}$
.
Claim 13 Every set
![]() $Y_{p,q}$
is closed in
$Y_{p,q}$
is closed in
![]() $\overline Y$
.
$\overline Y$
.
Let
![]() $\{y_n\}$
be a sequence in
$\{y_n\}$
be a sequence in
![]() $Y_{p,q}$
converging to
$Y_{p,q}$
converging to
![]() $y\in \overline Y$
. Suppose
$y\in \overline Y$
. Suppose
![]() $y\not \in Y_{p,q}$
. Then either
$y\not \in Y_{p,q}$
. Then either
![]() $supp(l_y)$
contains at least
$supp(l_y)$
contains at least
![]() $q+1$
points or
$q+1$
points or
![]() $a(y)>p$
. If
$a(y)>p$
. If
![]() $supp(l_y)$
contains at least
$supp(l_y)$
contains at least
![]() $q+1$
points
$q+1$
points
![]() $x_1,x_2,\ldots ,x_{q+1}$
, we choose disjoint neighborhoods
$x_1,x_2,\ldots ,x_{q+1}$
, we choose disjoint neighborhoods
![]() $O_i$
of
$O_i$
of
![]() $x_i$
,
$x_i$
,
![]() $i=1,\ldots ,q+1$
. By Claim 11, there is a neighborhood V of y such that
$i=1,\ldots ,q+1$
. By Claim 11, there is a neighborhood V of y such that
![]() $supp(l_z)\cap O_i\neq \varnothing $
for all i and
$supp(l_z)\cap O_i\neq \varnothing $
for all i and
![]() $z\in V$
. This implies that
$z\in V$
. This implies that
![]() $supp(l_{y_n})$
has at least
$supp(l_{y_n})$
has at least
![]() $q+1$
points for infinitely many n’s, a contradiction.
$q+1$
points for infinitely many n’s, a contradiction.
If
![]() $y\not \in Y_{p,q}$
and
$y\not \in Y_{p,q}$
and
![]() $a(y)>p$
, then there exists
$a(y)>p$
, then there exists
![]() $\overline f\in E(\overline X)$
such that
$\overline f\in E(\overline X)$
such that
![]() $|\overline f(x)|<1$
for all
$|\overline f(x)|<1$
for all
![]() $x\in supp(l_y)$
and
$x\in supp(l_y)$
and
![]() $|l_y(\overline f)|>p$
. Take a neighborhood U of
$|l_y(\overline f)|>p$
. Take a neighborhood U of
![]() $supp(l_y)$
with
$supp(l_y)$
with
![]() $U\subset \{x\in \overline X:|\overline f(x)|<1\}$
. Choose another neighborhood W of
$U\subset \{x\in \overline X:|\overline f(x)|<1\}$
. Choose another neighborhood W of
![]() $supp(l_y)$
with
$supp(l_y)$
with
![]() $\overline W\subset U$
. Next, there is
$\overline W\subset U$
. Next, there is
![]() $h\in E(X)$
such that
$h\in E(X)$
such that
![]() $\overline h(\overline W)=1$
,
$\overline h(\overline W)=1$
,
![]() $\overline h(\overline X\backslash U)=0,$
and
$\overline h(\overline X\backslash U)=0,$
and
![]() $h(x)\in [0,1]$
for all
$h(x)\in [0,1]$
for all
![]() $x\in X$
. Then,
$x\in X$
. Then,
![]() $\overline g=\overline {h\cdot f}\in E(\overline X)$
and
$\overline g=\overline {h\cdot f}\in E(\overline X)$
and
![]() $|\overline g(x)|<1$
for all
$|\overline g(x)|<1$
for all
![]() $x\in \overline X$
. Moreover,
$x\in \overline X$
. Moreover,
![]() $\overline g|W=\overline f|W$
. So, by Claim 10,
$\overline g|W=\overline f|W$
. So, by Claim 10,
![]() $|l_y(\overline g)|=|l_y(\overline f)|>p$
. Therefore,
$|l_y(\overline g)|=|l_y(\overline f)|>p$
. Therefore,
![]() $V=\{z\in \overline Y:|l_z(\overline g)|>p\}$
is a neighborhood of y in
$V=\{z\in \overline Y:|l_z(\overline g)|>p\}$
is a neighborhood of y in
![]() $\overline Y$
with
$\overline Y$
with
![]() $V\cap Y_{p,q}=\varnothing $
, a contradiction.
$V\cap Y_{p,q}=\varnothing $
, a contradiction.
According to Claim 12, for every
![]() $y\in Y,$
then there exist
$y\in Y,$
then there exist
![]() $p,q\in \mathbb N$
and real numbers
$p,q\in \mathbb N$
and real numbers
![]() $\lambda _i(y)$
such that for all
$\lambda _i(y)$
such that for all
![]() $\overline f\in E(\overline X),$
we have
$\overline f\in E(\overline X),$
we have
![]() $l_y(\overline f)=\sum _{i=1}^q\lambda _i(y)\overline f(x_i(y))$
with
$l_y(\overline f)=\sum _{i=1}^q\lambda _i(y)\overline f(x_i(y))$
with
![]() $a(y)=\sum _{i=1}^q|\lambda _i(y)|\leq p$
, where
$a(y)=\sum _{i=1}^q|\lambda _i(y)|\leq p$
, where
![]() $\{x_1(y),\ldots ,x_q(y)\}$
is the support
$\{x_1(y),\ldots ,x_q(y)\}$
is the support
![]() $supp(l_y)$
. Hence,
$supp(l_y)$
. Hence,
![]() $Y\subset \bigcup \{Y_{p,q}:p,q\in \mathbb N\}$
. For every
$Y\subset \bigcup \{Y_{p,q}:p,q\in \mathbb N\}$
. For every
![]() $p\geq 1$
and
$p\geq 1$
and
![]() $q\geq 2,$
we define
$q\geq 2,$
we define
Some of the sets
![]() $M(p,q)$
could be empty, but
$M(p,q)$
could be empty, but
![]() $Y\subset \bigcup \{M(p,q):p,q=1,2,\ldots \}$
. Indeed, by Claim 12, there exist
$Y\subset \bigcup \{M(p,q):p,q=1,2,\ldots \}$
. Indeed, by Claim 12, there exist
![]() $p,q$
with
$p,q$
with
![]() $|supp(l_y)|=q$
and
$|supp(l_y)|=q$
and
![]() $a(y)\leq p$
. Then,
$a(y)\leq p$
. Then,
![]() $y\in M(p,q)$
. Since each
$y\in M(p,q)$
. Since each
![]() $Y_{p,q}$
is closed,
$Y_{p,q}$
is closed,
![]() $M(p,q)=\bigcup _{n=1}^\infty F_n'(p,q)$
such that each
$M(p,q)=\bigcup _{n=1}^\infty F_n'(p,q)$
such that each
![]() $F_n'(p,q)$
is a compact subset of
$F_n'(p,q)$
is a compact subset of
![]() $\overline Y$
. We define
$\overline Y$
. We define
![]() $F_n(p,q)=\overline {Y\cap F_n'(p,q)}$
. Then,
$F_n(p,q)=\overline {Y\cap F_n'(p,q)}$
. Then,
![]() $Y\subset \bigcup \{F_n(p,q):n,p,q=1,2,\ldots \}$
. Obviously,
$Y\subset \bigcup \{F_n(p,q):n,p,q=1,2,\ldots \}$
. Obviously,
![]() $supp(l_y)$
consists of q different points for any
$supp(l_y)$
consists of q different points for any
![]() $y\in M(p,q)$
. So, we have a map
$y\in M(p,q)$
. So, we have a map
![]() $S_{p,q}:M(p,q)\to [\overline X]^q$
,
$S_{p,q}:M(p,q)\to [\overline X]^q$
,
![]() $S_{p,q}(y)=supp(l_y)$
. According to Claim 11,
$S_{p,q}(y)=supp(l_y)$
. According to Claim 11,
![]() $S_{p,q}$
is continuous when
$S_{p,q}$
is continuous when
![]() $[\overline X]^q$
is equipped with the Vietoris topology. For every
$[\overline X]^q$
is equipped with the Vietoris topology. For every
![]() $y\in M(p,q),$
let
$y\in M(p,q),$
let
![]() $S_{p,q}(y)=\{x_i(y)\}_{i=1}^q$
. Everywhere below, we consider the restriction
$S_{p,q}(y)=\{x_i(y)\}_{i=1}^q$
. Everywhere below, we consider the restriction
![]() $S_{p,q}|F_n(p,q)$
and for every
$S_{p,q}|F_n(p,q)$
and for every
![]() $z\in F_n(p,q)$
denote by
$z\in F_n(p,q)$
denote by
![]() $A(z)=\{y\in F_n(p,q):S_{p,q}(y)=S_{p,q}(z)\}$
the fiber
$A(z)=\{y\in F_n(p,q):S_{p,q}(y)=S_{p,q}(z)\}$
the fiber
![]() $S_{p,q}^{-1}(S_{p,q}(z))$
generated by z. Since
$S_{p,q}^{-1}(S_{p,q}(z))$
generated by z. Since
![]() $F_n(p,q)$
is compact and
$F_n(p,q)$
is compact and
![]() $S_{p,q}$
is continuous, each
$S_{p,q}$
is continuous, each
![]() $A(z)$
is a compact subset of
$A(z)$
is a compact subset of
![]() $F_n(p,q)$
.
$F_n(p,q)$
.
Claim 14 Let
![]() $z\in Y\cap F_n(p,q)$
. Then, for every
$z\in Y\cap F_n(p,q)$
. Then, for every
![]() $y\in A(z),$
there are real numbers
$y\in A(z),$
there are real numbers
![]() $\{\lambda _i(y)\}_{i=1}^{q}$
such that
$\{\lambda _i(y)\}_{i=1}^{q}$
such that
![]() $l_y(\overline f)=\sum _{i=1}^{q}\lambda _i(y)\overline f(x_i(z))$
, where
$l_y(\overline f)=\sum _{i=1}^{q}\lambda _i(y)\overline f(x_i(z))$
, where
![]() $S_{p,q}(z)=\{x_i(z)\}_{i=1}^{q}$
, and
$S_{p,q}(z)=\{x_i(z)\}_{i=1}^{q}$
, and
![]() $\sum _{i=1}^q|\lambda _i(y)|\leq p$
for all
$\sum _{i=1}^q|\lambda _i(y)|\leq p$
for all
![]() $\overline f\in E(\overline X)$
. Moreover, each
$\overline f\in E(\overline X)$
. Moreover, each
![]() $\lambda _i$
is a continuous real-valued function on
$\lambda _i$
is a continuous real-valued function on
![]() $A(z)$
.
$A(z)$
.
Choose neighborhoods
![]() $O_i$
of
$O_i$
of
![]() $x_i(z)$
in
$x_i(z)$
in
![]() $\overline X$
with disjoint closures and functions
$\overline X$
with disjoint closures and functions
![]() $\overline g_i\in E(\overline X)$
with
$\overline g_i\in E(\overline X)$
with
![]() $\overline g_i|O_i=1$
and
$\overline g_i|O_i=1$
and
![]() $\overline g_i|O_j=0$
if
$\overline g_i|O_j=0$
if
![]() $j\neq i$
(this can be done by choosing
$j\neq i$
(this can be done by choosing
![]() $g_i\in E(X)$
with
$g_i\in E(X)$
with
![]() $g_i(O_i\cap X)=1$
and
$g_i(O_i\cap X)=1$
and
![]() $g_i(O_j\cap X)=0$
when
$g_i(O_j\cap X)=0$
when
![]() $j\neq i$
). According to the proof of Claim 12, for every
$j\neq i$
). According to the proof of Claim 12, for every
![]() $y\in A(z)\cap Y$
and the real numbers
$y\in A(z)\cap Y$
and the real numbers
![]() $\lambda _i(y)=l_y(\overline g_i),$
we have
$\lambda _i(y)=l_y(\overline g_i),$
we have
![]() $l_y(\overline f)=\sum _{i=1}^{q}\lambda _i(y)\overline f(x_i(z))$
for all
$l_y(\overline f)=\sum _{i=1}^{q}\lambda _i(y)\overline f(x_i(z))$
for all
![]() $\overline f\in E(\overline X)$
. Let’s show this is true for all
$\overline f\in E(\overline X)$
. Let’s show this is true for all
![]() $y\in A(z)$
. So, fix
$y\in A(z)$
. So, fix
![]() $y\in A(z)\backslash Y$
and take a sequence
$y\in A(z)\backslash Y$
and take a sequence
![]() $\{y_m\}\subset Y\cap F_n(p,q)$
converging to y. Then, by Claim 12,
$\{y_m\}\subset Y\cap F_n(p,q)$
converging to y. Then, by Claim 12,
![]() $S_{p,q}(y_m)=\{x_i(y_m)\}_{i=1}^q\subset X$
and there are real numbers
$S_{p,q}(y_m)=\{x_i(y_m)\}_{i=1}^q\subset X$
and there are real numbers
![]() $\{\lambda _i(y_m)\}_{i=1}^q$
such that
$\{\lambda _i(y_m)\}_{i=1}^q$
such that
![]() $l_{y_m}(\overline f)=\sum _{i=1}^q\lambda _i(y_m)\overline f(x_i(y_m))$
for all
$l_{y_m}(\overline f)=\sum _{i=1}^q\lambda _i(y_m)\overline f(x_i(y_m))$
for all
![]() $\overline f\in E(\overline X)$
. On the other hand, since the map
$\overline f\in E(\overline X)$
. On the other hand, since the map
![]() $S_{p,q}$
is continuous, each sequence
$S_{p,q}$
is continuous, each sequence
![]() $\{x_i(y_m)\}_{m=1}^\infty $
converges to
$\{x_i(y_m)\}_{m=1}^\infty $
converges to
![]() $x_i(y)=x_i(z)$
,
$x_i(y)=x_i(z)$
,
![]() $i=1,\ldots ,q$
. So, we can assume that
$i=1,\ldots ,q$
. So, we can assume that
![]() $\{x_i(y_m)\}_{m=1}^\infty \subset O_i$
. Consequently,
$\{x_i(y_m)\}_{m=1}^\infty \subset O_i$
. Consequently,
![]() $l_{y_m}(\overline g_i)=\lambda _i(y_m)$
and
$l_{y_m}(\overline g_i)=\lambda _i(y_m)$
and
![]() $\lim _m\lambda _i(y_m)=l_y(\overline g_i)$
. Since
$\lim _m\lambda _i(y_m)=l_y(\overline g_i)$
. Since
![]() $\{y_m\}\subset Y\cap Y_{p,q}$
,
$\{y_m\}\subset Y\cap Y_{p,q}$
,
![]() $\sum _{i=1}^q|\lambda _i(y_m)|\leq p$
for each m (see Claim 12). Hence,
$\sum _{i=1}^q|\lambda _i(y_m)|\leq p$
for each m (see Claim 12). Hence,
![]() $\sum _{i=1}^q|l_y(\overline g_i)|\leq p$
. Denoting
$\sum _{i=1}^q|l_y(\overline g_i)|\leq p$
. Denoting
![]() $\lambda _i(y)=l_y(\overline g_i)$
, we obtain
$\lambda _i(y)=l_y(\overline g_i)$
, we obtain
![]() $\sum _{i=1}^q|\lambda _i(y)|\leq p$
. The last inequality means that all
$\sum _{i=1}^q|\lambda _i(y)|\leq p$
. The last inequality means that all
![]() $\lambda _i(y)$
are real numbers. Since
$\lambda _i(y)$
are real numbers. Since
![]() $\lim _m\overline f(x_i(y_m))=\overline f(x_i(y))$
for all
$\lim _m\overline f(x_i(y_m))=\overline f(x_i(y))$
for all
![]() $\overline f\in E(\overline X)$
and each
$\overline f\in E(\overline X)$
and each
![]() $\overline f(x_i(y))$
is a real number (recall that
$\overline f(x_i(y))$
is a real number (recall that
![]() $z\in Y$
, so by Claim 12,
$z\in Y$
, so by Claim 12,
![]() $x_i(z)=x_i(y)\in X$
), we have
$x_i(z)=x_i(y)\in X$
), we have
![]() $l_y(\overline f)=\lim l_{y_m}(\overline f)=\sum _{i=1}^q\lambda _i(y)\overline f(x_i(y))$
.
$l_y(\overline f)=\lim l_{y_m}(\overline f)=\sum _{i=1}^q\lambda _i(y)\overline f(x_i(y))$
.
Finally, the equality
![]() $\lambda _i(y)=\overline {\varphi (g_i)}(y)$
implies that
$\lambda _i(y)=\overline {\varphi (g_i)}(y)$
implies that
![]() $\lambda _i$
are continuous on
$\lambda _i$
are continuous on
![]() $A(z)$
.
$A(z)$
.
Claim 15 Let
![]() $A(z)=\{y\in F_n(p,q):S_{p,q}(y)=S_{p,q}(z)\}$
with
$A(z)=\{y\in F_n(p,q):S_{p,q}(y)=S_{p,q}(z)\}$
with
![]() $z\in Y\cap F_n(p,q)$
. Then, there is a linear continuous map
$z\in Y\cap F_n(p,q)$
. Then, there is a linear continuous map
![]() $\varphi _z:C_p(S_{p,q}(z))\to C_p(A(z))$
such that
$\varphi _z:C_p(S_{p,q}(z))\to C_p(A(z))$
such that
![]() $\varphi _z(C(S_{p,q}(z)))$
is dense in
$\varphi _z(C(S_{p,q}(z)))$
is dense in
![]() $C_p(A(z))$
.
$C_p(A(z))$
.
Following the previous notations, for every
![]() $h\in C(S_{p,q}(z))$
and
$h\in C(S_{p,q}(z))$
and
![]() $y\in A(z),$
we define
$y\in A(z),$
we define
![]() $\varphi _z(h)(y)=\sum _{i=1}^q\lambda _i(y)h(x_i(z))$
. Because
$\varphi _z(h)(y)=\sum _{i=1}^q\lambda _i(y)h(x_i(z))$
. Because
![]() $\lambda _i$
are continuous real-valued functions on
$\lambda _i$
are continuous real-valued functions on
![]() $A(z)$
, so is each
$A(z)$
, so is each
![]() $\varphi _z(h)$
. Continuity of
$\varphi _z(h)$
. Continuity of
![]() $\varphi _z$
with respect to the pointwise convergence topology is obvious. Let’s show that
$\varphi _z$
with respect to the pointwise convergence topology is obvious. Let’s show that
![]() $\varphi _z(C(S_{p,q}(z)))$
is dense in
$\varphi _z(C(S_{p,q}(z)))$
is dense in
![]() $C_p(A(z))$
. Indeed, take
$C_p(A(z))$
. Indeed, take
![]() $\theta \in C_p(A(z))$
and its neighborhood
$\theta \in C_p(A(z))$
and its neighborhood
![]() $V\subset C_p(A(z))$
. Then extend
$V\subset C_p(A(z))$
. Then extend
![]() $\theta $
to a function
$\theta $
to a function
![]() $\overline \theta \in C(\overline Y)$
. Because the set of real-valued elements of
$\overline \theta \in C(\overline Y)$
. Because the set of real-valued elements of
![]() $E_p(\overline Y)$
is dense in
$E_p(\overline Y)$
is dense in
![]() $C_p(\overline Y)$
, there is
$C_p(\overline Y)$
, there is
![]() $\overline g\in E_p(\overline Y)$
with
$\overline g\in E_p(\overline Y)$
with
![]() $\overline g|A(z)\in V$
, so
$\overline g|A(z)\in V$
, so
![]() $\overline g(y)\in \mathbb R$
for all
$\overline g(y)\in \mathbb R$
for all
![]() $y\in \overline Y$
. Next, choose
$y\in \overline Y$
. Next, choose
![]() $f\in E(X)$
such that
$f\in E(X)$
such that
![]() $\varphi (f)=g$
. Since
$\varphi (f)=g$
. Since
![]() $z\in Y$
, each
$z\in Y$
, each
![]() $x_i(z)\in X$
. So, all
$x_i(z)\in X$
. So, all
![]() $\overline f(x_i(z))$
are real numbers. Then,
$\overline f(x_i(z))$
are real numbers. Then,
![]() $h=\overline f|S_{p,q}(z)\in C(S_{p,q}(z))$
and, according to Claim 14, we have
$h=\overline f|S_{p,q}(z)\in C(S_{p,q}(z))$
and, according to Claim 14, we have
![]() $\varphi _z(h)=\overline g|A(z)$
.
$\varphi _z(h)=\overline g|A(z)$
.
Claim 16 The fibers
![]() $A(z)$
of the map
$A(z)$
of the map
![]() $S_{p,q}: F_n(p,q)\to [\overline X]^q$
are zero-dimensional for all
$S_{p,q}: F_n(p,q)\to [\overline X]^q$
are zero-dimensional for all
![]() $z\in Y\cap F_n(p,q)$
.
$z\in Y\cap F_n(p,q)$
.
Since
![]() $|S_{p,q}(z)|=q$
,
$|S_{p,q}(z)|=q$
,
![]() $C_p(S_{p,q}(z))$
is isomorphic to
$C_p(S_{p,q}(z))$
is isomorphic to
![]() $\mathbb R^q$
. Hence, Claim 15 together with basic facts from linear algebra imply that
$\mathbb R^q$
. Hence, Claim 15 together with basic facts from linear algebra imply that
![]() $|A(z)|\leq q$
, in particular,
$|A(z)|\leq q$
, in particular,
![]() $A(z)$
is zero-dimensional.
$A(z)$
is zero-dimensional.
Now, we can complete the proof of Proposition 4.1. As in the proof of Proposition 2.1, using that
![]() $\overline X^q\in \mathcal P$
, we can show that
$\overline X^q\in \mathcal P$
, we can show that
![]() $[\overline X]^q\in \mathcal P$
. Therefore, condition (c’) implies that each
$[\overline X]^q\in \mathcal P$
. Therefore, condition (c’) implies that each
![]() $F_n(p,q)$
has also the property
$F_n(p,q)$
has also the property
![]() $\mathcal P$
, and so does
$\mathcal P$
, and so does
![]() $Y_n(p,q)=F_n(p,q)\cap Y$
. Finally, since Y is the union of its closed subsets
$Y_n(p,q)=F_n(p,q)\cap Y$
. Finally, since Y is the union of its closed subsets
![]() $Y_n(p,q)$
, we conclude that
$Y_n(p,q)$
, we conclude that
![]() $Y\in \mathcal P$
.
$Y\in \mathcal P$
.
Lemma 4.2 For every countable set
![]() $\Phi '\subset C(\beta Y,\overline {\mathbb R})$
there is a countable set
$\Phi '\subset C(\beta Y,\overline {\mathbb R})$
there is a countable set
![]() $\Phi \subset C(\beta Y,\overline {\mathbb R})$
containing
$\Phi \subset C(\beta Y,\overline {\mathbb R})$
containing
![]() $\Phi '$
such that
$\Phi '$
such that
![]() $(\triangle \Phi )(\beta Y)$
is homeomorphic to
$(\triangle \Phi )(\beta Y)$
is homeomorphic to
![]() $(\triangle \Phi ')(\beta Y)$
and the set of real-valued elements of
$(\triangle \Phi ')(\beta Y)$
and the set of real-valued elements of
![]() $E_\Phi =\{\pi _{\overline g}:\overline g\in \Phi \}$
is dense in
$E_\Phi =\{\pi _{\overline g}:\overline g\in \Phi \}$
is dense in
![]() $C_p((\triangle \Phi )(\beta Y))$
.
$C_p((\triangle \Phi )(\beta Y))$
.
Proof Let
![]() $\phi '=\triangle \Phi '$
. Since
$\phi '=\triangle \Phi '$
. Since
![]() $\Phi '$
is countable,
$\Phi '$
is countable,
![]() $\phi '(\beta Y)$
is a metrizable compactum. Hence, by [Reference Gul’ko7, Proposition 1.2], there is a countable
$\phi '(\beta Y)$
is a metrizable compactum. Hence, by [Reference Gul’ko7, Proposition 1.2], there is a countable
![]() $QS$
-algebra
$QS$
-algebra
![]() $E\subset C(\phi '(\beta Y))$
. Let
$E\subset C(\phi '(\beta Y))$
. Let
![]() $\Phi =\Phi '\cup \{g\circ \phi ':g\in E\}$
. Since the functions of E separate the points and closed subsets of
$\Phi =\Phi '\cup \{g\circ \phi ':g\in E\}$
. Since the functions of E separate the points and closed subsets of
![]() $\phi '(\beta Y)$
,
$\phi '(\beta Y)$
,
![]() $(\triangle \Phi )(\beta Y)$
is homeomorphic to
$(\triangle \Phi )(\beta Y)$
is homeomorphic to
![]() $\phi '(\beta Y)$
. Since E is a
$\phi '(\beta Y)$
. Since E is a
![]() $QS$
-algebra on
$QS$
-algebra on
![]() $\phi '(\beta Y)$
, E is a dense subset of
$\phi '(\beta Y)$
, E is a dense subset of
![]() $C_p(\phi '(\beta Y))$
. Clearly, E is a subset of
$C_p(\phi '(\beta Y))$
. Clearly, E is a subset of
![]() $E_\Phi $
and consists of real-valued functions.
$E_\Phi $
and consists of real-valued functions.
Lemma 4.3 Let X be a zero-dimensional space and
![]() $\Psi '\subset C(X)$
be a countable set. Then, there is a countable admissible set
$\Psi '\subset C(X)$
be a countable set. Then, there is a countable admissible set
![]() $\Psi \subset C(X)$
containing
$\Psi \subset C(X)$
containing
![]() $\Psi '$
and a zero-dimensional metrizable compactification
$\Psi '$
and a zero-dimensional metrizable compactification
![]() $\overline X_\Psi $
of
$\overline X_\Psi $
of
![]() $X_\Psi =(\triangle \Psi )(X)$
having a countable base
$X_\Psi =(\triangle \Psi )(X)$
having a countable base
![]() $\mathcal B$
such that:
$\mathcal B$
such that:
-
•
 $\overline X_\Psi =(\triangle \overline \Psi )(\beta X)$
with
$\overline X_\Psi =(\triangle \overline \Psi )(\beta X)$
with
 $\overline \Psi =\{\overline f:f\in \Psi \}\subset C(\beta X,\overline {\mathbb R})$
;
$\overline \Psi =\{\overline f:f\in \Psi \}\subset C(\beta X,\overline {\mathbb R})$
; -
• each
 $\pi _f$
,
$\pi _f$
,
 $f\in \Psi $
, is extendable to a map
$f\in \Psi $
, is extendable to a map
 $\overline \pi _f:\overline X_\Psi \to \overline {\mathbb R}$
;
$\overline \pi _f:\overline X_\Psi \to \overline {\mathbb R}$
; -
•
 $E(X_\Psi )=\{\pi _f:f\in \Psi \}$
is a countable
$E(X_\Psi )=\{\pi _f:f\in \Psi \}$
is a countable
 $QS$
-algebra on
$QS$
-algebra on
 $X_\Psi $
and
$X_\Psi $
and
 $E(\overline X_\Psi )=\{\overline \pi _f:f\in \Psi \}$
contains a countable
$E(\overline X_\Psi )=\{\overline \pi _f:f\in \Psi \}$
contains a countable
 $QS$
-algebra on
$QS$
-algebra on
 $\overline X_\Psi $
satisfying condition (2.3);
$\overline X_\Psi $
satisfying condition (2.3); -
• for every finite open cover
 $\gamma $
of
$\gamma $
of
 $\overline X_\Psi $
with elements from
$\overline X_\Psi $
with elements from
 $\mathcal B,$
the family
$\mathcal B,$
the family
 $E(\overline X_\Psi )$
contains a partition of unity subordinated to
$E(\overline X_\Psi )$
contains a partition of unity subordinated to
 $\gamma $
.
$\gamma $
.
Proof We first choose a countable admissible set
![]() $\Psi _0\subset C(X)$
such that
$\Psi _0\subset C(X)$
such that
![]() $\dim (\triangle \Psi _0)(X)=0$
and
$\dim (\triangle \Psi _0)(X)=0$
and
![]() $\Psi '\subset \Psi _0$
(see (3.2) and (3.3)). Then, by Lemma 3.2, there is a metrizable compactification
$\Psi '\subset \Psi _0$
(see (3.2) and (3.3)). Then, by Lemma 3.2, there is a metrizable compactification
![]() $Z_0$
of
$Z_0$
of
![]() $X_0=(\triangle \Psi _0)(X)$
with
$X_0=(\triangle \Psi _0)(X)$
with
![]() $\dim Z_0=0$
such that each
$\dim Z_0=0$
such that each
![]() $\pi _f$
,
$\pi _f$
,
![]() $f\in \Psi _0$
, is extendable to a map
$f\in \Psi _0$
, is extendable to a map
![]() $\overline \pi _f:Z_0\to \overline {\mathbb R}$
. Choose a countable
$\overline \pi _f:Z_0\to \overline {\mathbb R}$
. Choose a countable
![]() $QS$
-algebra
$QS$
-algebra
![]() $C_0\subset C(Z_0)$
satisfying condition (2.3) (that can be done because
$C_0\subset C(Z_0)$
satisfying condition (2.3) (that can be done because
![]() $Z_0$
has a countable base, see the explanations in
$Z_0$
has a countable base, see the explanations in
![]() $(2.3)$
). Let
$(2.3)$
). Let
![]() $\mathcal B_0$
be a countable base for
$\mathcal B_0$
be a countable base for
![]() $Z_0$
and for every finite open cover
$Z_0$
and for every finite open cover
![]() $\gamma $
of
$\gamma $
of
![]() $Z_0$
consisting of open sets from
$Z_0$
consisting of open sets from
![]() $\mathcal B_0$
fix a partition of unity
$\mathcal B_0$
fix a partition of unity
![]() $\alpha _\gamma $
subordinated to
$\alpha _\gamma $
subordinated to
![]() $\gamma $
. Because the family
$\gamma $
. Because the family
![]() $\Omega _0$
of all finite open covers of
$\Omega _0$
of all finite open covers of
![]() $Z_0$
consisting of elements of
$Z_0$
consisting of elements of
![]() $\mathcal B_0$
is countable, so is the family
$\mathcal B_0$
is countable, so is the family
![]() $E(Z_0)=\{\overline f:f\in \Psi _0\}\cup \{\alpha _\gamma :\gamma \in \Omega _0\}\cup C_0$
. The set
$E(Z_0)=\{\overline f:f\in \Psi _0\}\cup \{\alpha _\gamma :\gamma \in \Omega _0\}\cup C_0$
. The set
![]() $E_0=\{h|X_0:h\in E(Z_0)\}$
may not be a
$E_0=\{h|X_0:h\in E(Z_0)\}$
may not be a
![]() $QS$
-algebra on
$QS$
-algebra on
![]() $X_0$
but, according to [Reference Gul’ko7, Proposition 1.2], there exists a countable
$X_0$
but, according to [Reference Gul’ko7, Proposition 1.2], there exists a countable
![]() $QS$
-algebra
$QS$
-algebra
![]() $\Theta _1$
on
$\Theta _1$
on
![]() $X_0$
containing
$X_0$
containing
![]() $E_0$
as a proper subset. For every
$E_0$
as a proper subset. For every
![]() $h\in \Theta _{1}$
, the function
$h\in \Theta _{1}$
, the function
![]() $h\circ (\triangle \Psi _0):X\to {\mathbb R}$
can be extended to a map
$h\circ (\triangle \Psi _0):X\to {\mathbb R}$
can be extended to a map
![]() $\widetilde h:\beta X\to \overline {\mathbb R}$
and let
$\widetilde h:\beta X\to \overline {\mathbb R}$
and let
![]() $P_h=\widetilde h(\beta X)$
. Because
$P_h=\widetilde h(\beta X)$
. Because
![]() $\{h|X_0:h\in C_0\}\subset \Theta _1$
and it separates the points and the closed sets of
$\{h|X_0:h\in C_0\}\subset \Theta _1$
and it separates the points and the closed sets of
![]() $X_0$
, by Lemma 3.2, there is a metrizable compactification
$X_0$
, by Lemma 3.2, there is a metrizable compactification
![]() $Z_1$
of
$Z_1$
of
![]() $X_0$
such that
$X_0$
such that
![]() $\dim Z_1=0$
, each
$\dim Z_1=0$
, each
![]() $h\in \Theta _1$
is extendable to a map
$h\in \Theta _1$
is extendable to a map
![]() $\overline h:Z_1\to \overline {\mathbb R}$
. The compactification
$\overline h:Z_1\to \overline {\mathbb R}$
. The compactification
![]() $Z_1$
is a closed subset of the product
$Z_1$
is a closed subset of the product
![]() $Z_0\times \prod _{h\in \Theta _1}P_h$
. Then, the projection
$Z_0\times \prod _{h\in \Theta _1}P_h$
. Then, the projection
![]() $Z_0\times \prod _{h\in \Theta _1}P_h\to Z_0$
provides a map
$Z_0\times \prod _{h\in \Theta _1}P_h\to Z_0$
provides a map
![]() $\theta ^1_0:Z_1\to Z_0$
such that
$\theta ^1_0:Z_1\to Z_0$
such that
![]() $\theta ^1_0\circ j_1=j_0$
with
$\theta ^1_0\circ j_1=j_0$
with
![]() $j_1:X_0\to Z_1$
and
$j_1:X_0\to Z_1$
and
![]() $j_0:X_0\to Z_0$
being the corresponding embeddings.
$j_0:X_0\to Z_0$
being the corresponding embeddings.
Next, fix a base
![]() $\mathcal B_1$
on
$\mathcal B_1$
on
![]() $Z_1$
containing all sets
$Z_1$
containing all sets
![]() $(\theta ^1_0)^{-1}(U)$
,
$(\theta ^1_0)^{-1}(U)$
,
![]() $U\in \mathcal B_0$
, which is closed under finite intersections, and consider the family
$U\in \mathcal B_0$
, which is closed under finite intersections, and consider the family
![]() $\Omega _1$
of all finite open covers of
$\Omega _1$
of all finite open covers of
![]() $Z_1$
consisting of sets from
$Z_1$
consisting of sets from
![]() $\mathcal B_1$
. For each
$\mathcal B_1$
. For each
![]() $\gamma \in \Omega _1$
fix a partition of unity
$\gamma \in \Omega _1$
fix a partition of unity
![]() $\alpha _\gamma $
subordinated to
$\alpha _\gamma $
subordinated to
![]() $\gamma $
and let
$\gamma $
and let
![]() $E(Z_1)=\{\overline h:h\in \Theta _1\}\cup \{\alpha _\gamma :\gamma \in \Omega _1\}\cup C_1$
and
$E(Z_1)=\{\overline h:h\in \Theta _1\}\cup \{\alpha _\gamma :\gamma \in \Omega _1\}\cup C_1$
and
![]() $E_1=\{f|X_0:f\in E(Z_1)\}$
, where
$E_1=\{f|X_0:f\in E(Z_1)\}$
, where
![]() $C_1\subset C(Z_1)$
is a countable
$C_1\subset C(Z_1)$
is a countable
![]() $QS$
-algebra of
$QS$
-algebra of
![]() $Z_1$
satisfying condition (2.3) such that
$Z_1$
satisfying condition (2.3) such that
![]() $\{h\circ \theta ^1_0:h\in C_0\}\subset C_1$
. We construct by induction an increasing sequence
$\{h\circ \theta ^1_0:h\in C_0\}\subset C_1$
. We construct by induction an increasing sequence
![]() $\{\Theta _n\}$
of countable
$\{\Theta _n\}$
of countable
![]() $QS$
-algebras on
$QS$
-algebras on
![]() $X_0$
, zero-dimensional metrizable compactifications
$X_0$
, zero-dimensional metrizable compactifications
![]() $Z_n$
of
$Z_n$
of
![]() $X_0$
with a countable base
$X_0$
with a countable base
![]() $\mathcal B_n$
, countable
$\mathcal B_n$
, countable
![]() $QS$
-algebras
$QS$
-algebras
![]() $C_n\subset C(Z_n)$
on
$C_n\subset C(Z_n)$
on
![]() $Z_n$
, countable families
$Z_n$
, countable families
![]() $E(Z_n)\subset C(Z_n,\overline {\mathbb R}),$
and surjective maps
$E(Z_n)\subset C(Z_n,\overline {\mathbb R}),$
and surjective maps
![]() $\theta ^{n+1}_n:Z_{n+1}\to Z_{n}$
such that:
$\theta ^{n+1}_n:Z_{n+1}\to Z_{n}$
such that:
-
(1)
 $\mathcal B_{n+1}$
contains all inverse images
$\mathcal B_{n+1}$
contains all inverse images
 $(\theta ^{n+1}_n)^{-1}(U)$
,
$(\theta ^{n+1}_n)^{-1}(U)$
,
 $U\in \mathcal B_{n}$
, and is closed under finite intersections;
$U\in \mathcal B_{n}$
, and is closed under finite intersections; -
(2)
 $C_{n+1}$
satisfies condition (2.3) and
$C_{n+1}$
satisfies condition (2.3) and
 $\{h\circ \theta ^{n+1}_n:h\in C_{n}\}\subset C_{n+1}$
;
$\{h\circ \theta ^{n+1}_n:h\in C_{n}\}\subset C_{n+1}$
; -
(3) every
 $Z_{n+1}$
is a zero-dimensional metrizable compactification of
$Z_{n+1}$
is a zero-dimensional metrizable compactification of
 $X_0$
such that every
$X_0$
such that every
 $h\in \Theta _{n+1}$
is extendable to a map
$h\in \Theta _{n+1}$
is extendable to a map
 $\overline h\in C(Z_{n+1},\overline {\mathbb R})$
;
$\overline h\in C(Z_{n+1},\overline {\mathbb R})$
; -
(4)
 $E(Z_{n+1})=\{\overline h:h\in \Theta _{n+1}\}\cup \{\alpha _\gamma :\gamma \in \Omega _{n+1}\}\cup C_{n+1}$
, where
$E(Z_{n+1})=\{\overline h:h\in \Theta _{n+1}\}\cup \{\alpha _\gamma :\gamma \in \Omega _{n+1}\}\cup C_{n+1}$
, where
 $\Omega _{n+1}$
is the family of all finite open covers
$\Omega _{n+1}$
is the family of all finite open covers
 $\gamma $
of
$\gamma $
of
 $Z_{n+1}$
with elements from
$Z_{n+1}$
with elements from
 $\mathcal B_{n+1}$
and
$\mathcal B_{n+1}$
and
 $\alpha _\gamma $
is a partition of unity subordinated to
$\alpha _\gamma $
is a partition of unity subordinated to
 $\gamma $
;
$\gamma $
; -
(5)
 $E_n=\{f|X_0:f\in E(Z_n)\}\subset \Theta _{n+1}$
.
$E_n=\{f|X_0:f\in E(Z_n)\}\subset \Theta _{n+1}$
.
If the construction is performed for all
![]() $k\leq n$
, let
$k\leq n$
, let
![]() $E_n=\{h|X_0:\overline h\in E(Z_n)\}$
and
$E_n=\{h|X_0:\overline h\in E(Z_n)\}$
and
![]() $\Theta _{n+1}$
be a countable
$\Theta _{n+1}$
be a countable
![]() $QS$
-algebra on
$QS$
-algebra on
![]() $X_0$
with
$X_0$
with
![]() $E_n\subset \Theta _{n+1}$
. For every
$E_n\subset \Theta _{n+1}$
. For every
![]() $h\in \Theta _{n+1}$
, the function
$h\in \Theta _{n+1}$
, the function
![]() $h\circ (\triangle \Psi _0):X\to {\mathbb R}$
can be extended to a map
$h\circ (\triangle \Psi _0):X\to {\mathbb R}$
can be extended to a map
![]() $\widetilde h:\beta X\to \overline {\mathbb R}$
and let
$\widetilde h:\beta X\to \overline {\mathbb R}$
and let
![]() $P_h=\widetilde h(\beta X)$
. By Lemma 3.2, there exists a metrizable compactification
$P_h=\widetilde h(\beta X)$
. By Lemma 3.2, there exists a metrizable compactification
![]() $Z_{n+1}$
of
$Z_{n+1}$
of
![]() $X_0$
such that
$X_0$
such that
![]() ${\dim Z_{n+1}=0}$
and each
${\dim Z_{n+1}=0}$
and each
![]() $h\in \Theta _{n+1}$
is extendable to a map
$h\in \Theta _{n+1}$
is extendable to a map
![]() $\overline h:Z_{n+1}\to \overline {\mathbb R}$
. The space
$\overline h:Z_{n+1}\to \overline {\mathbb R}$
. The space
![]() $Z_{n+1}$
is a closed subset of
$Z_{n+1}$
is a closed subset of
![]() $Z_n\times \prod _{h\in \Theta _{n+1}}P_h$
. So, the projection
$Z_n\times \prod _{h\in \Theta _{n+1}}P_h$
. So, the projection
![]() $Z_n\times \prod _{h\in \Theta _{n+1}}P_h\to Z_n$
determines a map
$Z_n\times \prod _{h\in \Theta _{n+1}}P_h\to Z_n$
determines a map
![]() $\theta ^{n+1}_n:Z_{n+1}\to Z_n$
such that
$\theta ^{n+1}_n:Z_{n+1}\to Z_n$
such that
![]() $\theta ^{n+1}_{n}\circ j_{n+1}=j_{n}$
, where
$\theta ^{n+1}_{n}\circ j_{n+1}=j_{n}$
, where
![]() $j_{n+1}:X_0\to Z_{n+1}$
and
$j_{n+1}:X_0\to Z_{n+1}$
and
![]() $j_{n}:X_0\to Z_{n}$
are the corresponding embeddings. Next, choose a base
$j_{n}:X_0\to Z_{n}$
are the corresponding embeddings. Next, choose a base
![]() $\mathcal B_{n+1}$
of
$\mathcal B_{n+1}$
of
![]() $Z_{n+1}$
, a countable
$Z_{n+1}$
, a countable
![]() $QS$
-algebra
$QS$
-algebra
![]() $C_{n+1}\subset C(Z_{n+1}),$
and a countable family
$C_{n+1}\subset C(Z_{n+1}),$
and a countable family
![]() $E(Z_{n+1})$
satisfying conditions (1)–(5).
$E(Z_{n+1})$
satisfying conditions (1)–(5).
Since
![]() $\{\Theta _n\}$
is an increasing sequence of
$\{\Theta _n\}$
is an increasing sequence of
![]() $QS$
-algebras on
$QS$
-algebras on
![]() $X_0$
,
$X_0$
,
![]() $\Theta =\bigcup _n\Theta _n$
is also a countable
$\Theta =\bigcup _n\Theta _n$
is also a countable
![]() $QS$
-algebra on
$QS$
-algebra on
![]() $X_0$
, and the limit space Z of the inverse sequence
$X_0$
, and the limit space Z of the inverse sequence
![]() ${S=\{Z_n,\theta ^n_{n-1}\}}$
is zero-dimensional. Because
${S=\{Z_n,\theta ^n_{n-1}\}}$
is zero-dimensional. Because
![]() $\theta ^{n+1}_{n}\circ j_{n+1}=j_{n}$
with
$\theta ^{n+1}_{n}\circ j_{n+1}=j_{n}$
with
![]() $j_{n+1}:X_0\to Z_{n+1}$
and
$j_{n+1}:X_0\to Z_{n+1}$
and
![]() $j_{n}:X_0\to Z_{n}$
being embeddings, there is an embedding
$j_{n}:X_0\to Z_{n}$
being embeddings, there is an embedding
![]() $j:X_0\to Z$
such that
$j:X_0\to Z$
such that
![]() $\theta _n\circ j=j_n$
, where
$\theta _n\circ j=j_n$
, where
![]() $\theta _n:Z\to Z_n$
is the projection in S. So, Z is a compactification of
$\theta _n:Z\to Z_n$
is the projection in S. So, Z is a compactification of
![]() $X_0$
and every
$X_0$
and every
![]() $h\in \Theta $
is extendable to a map
$h\in \Theta $
is extendable to a map
![]() $\overline {\overline h}:Z\to \overline {\mathbb R}$
. Indeed, if
$\overline {\overline h}:Z\to \overline {\mathbb R}$
. Indeed, if
![]() $h\in \Theta _n$
, then h can be extended to a map
$h\in \Theta _n$
, then h can be extended to a map
![]() $\overline h:Z_n\to \overline {\mathbb R}$
and
$\overline h:Z_n\to \overline {\mathbb R}$
and
![]() $\overline {\overline h}=\overline h\circ \theta _n$
is an extension of h over Z. Hence,
$\overline {\overline h}=\overline h\circ \theta _n$
is an extension of h over Z. Hence,
![]() $\Theta =\{g|Z:g\in E(Z)\}$
, where
$\Theta =\{g|Z:g\in E(Z)\}$
, where
![]() $E(Z)=\bigcup _n\{h\circ \theta _n:h\in E(Z_n)\}$
.
$E(Z)=\bigcup _n\{h\circ \theta _n:h\in E(Z_n)\}$
.
Denote
![]() $C_n'=\{h\circ \theta _n:h\in C_n\}$
,
$C_n'=\{h\circ \theta _n:h\in C_n\}$
,
![]() $n\geq 0$
. Because
$n\geq 0$
. Because
![]() $\{h\circ \theta ^n_{n-1}:h\in C_{n-1}\}\subset C_n$
, the sequence
$\{h\circ \theta ^n_{n-1}:h\in C_{n-1}\}\subset C_n$
, the sequence
![]() $\{C^{\prime }_n\}$
is increasing and
$\{C^{\prime }_n\}$
is increasing and
![]() $C=\bigcup _n C^{\prime }_n$
is closed under multiplications, additions, and additions by rational numbers. To show it a
$C=\bigcup _n C^{\prime }_n$
is closed under multiplications, additions, and additions by rational numbers. To show it a
![]() $QS$
-algebra on
$QS$
-algebra on
![]() $Z,$
we need to prove that for every point
$Z,$
we need to prove that for every point
![]() $z\in Z$
and its neighborhood
$z\in Z$
and its neighborhood
![]() $U\subset Z,$
there is
$U\subset Z,$
there is
![]() $h\in C$
such that
$h\in C$
such that
![]() $h(z)=1$
and
$h(z)=1$
and
![]() $h(Z\backslash U)=0$
. But that follows from condition (2.3), so let show that C satisfies condition (2.3). To this end, take a compact set
$h(Z\backslash U)=0$
. But that follows from condition (2.3), so let show that C satisfies condition (2.3). To this end, take a compact set
![]() $K\subset Z$
and an open set
$K\subset Z$
and an open set
![]() $W\subset Z$
containing K. Then, there exist n, a compact set
$W\subset Z$
containing K. Then, there exist n, a compact set
![]() $K_n\subset Z_n$
and open set
$K_n\subset Z_n$
and open set
![]() $W_n\subset Z_n$
containing
$W_n\subset Z_n$
containing
![]() $K_n$
such that
$K_n$
such that
![]() $K\subset \theta ^{-1}(K_n)\subset \theta ^{-1}(W_n)\subset W$
. Since
$K\subset \theta ^{-1}(K_n)\subset \theta ^{-1}(W_n)\subset W$
. Since
![]() $C_n$
satisfies condition (2.3), there is
$C_n$
satisfies condition (2.3), there is
![]() $h\in C_n$
with
$h\in C_n$
with
![]() $h|K_n=1$
,
$h|K_n=1$
,
![]() $h|(Z_n\backslash W_n)=0$
and
$h|(Z_n\backslash W_n)=0$
and
![]() $h(z)\in [0,1]$
for all
$h(z)\in [0,1]$
for all
![]() $z\in Z_n$
. Then,
$z\in Z_n$
. Then,
![]() $h'=\theta _n\circ h\in C$
,
$h'=\theta _n\circ h\in C$
,
![]() $h':Z\to [0,1]$
,
$h':Z\to [0,1]$
,
![]() $h'|K=1$
and
$h'|K=1$
and
![]() $h'|(X\backslash W)=0$
.
$h'|(X\backslash W)=0$
.
Recall that all finite intersections
![]() $U=\bigcap _{i=1}^k\theta _i^{-1}(U_i)$
with
$U=\bigcap _{i=1}^k\theta _i^{-1}(U_i)$
with
![]() $U_i\in \mathcal B_i$
form a base
$U_i\in \mathcal B_i$
form a base
![]() $\mathcal B$
for Z. Because of the choice of all
$\mathcal B$
for Z. Because of the choice of all
![]() $\mathcal B_i$
, see condition (1),
$\mathcal B_i$
, see condition (1),
![]() $\mathcal B$
consists of all sets of the form
$\mathcal B$
consists of all sets of the form
![]() ${U=\theta _n^{-1}(U_n)}$
with
${U=\theta _n^{-1}(U_n)}$
with
![]() $U_n\in \mathcal B_n$
,
$U_n\in \mathcal B_n$
,
![]() $n\in \mathbb N$
. Let’s show that for any finite open cover
$n\in \mathbb N$
. Let’s show that for any finite open cover
![]() $\gamma $
of Z consisting of sets from
$\gamma $
of Z consisting of sets from
![]() $\mathcal B$
, the set
$\mathcal B$
, the set
![]() $E(Z)$
contains a partition of unity subordinated to
$E(Z)$
contains a partition of unity subordinated to
![]() $\gamma $
. Indeed, for any such a cover
$\gamma $
. Indeed, for any such a cover
![]() $\gamma =\{U_1,\ldots ,U_k\},$
there is n and a cover
$\gamma =\{U_1,\ldots ,U_k\},$
there is n and a cover
![]() $\gamma _n=\{U_1^n,\ldots ,U_k^n\}\in \Omega _n$
such that
$\gamma _n=\{U_1^n,\ldots ,U_k^n\}\in \Omega _n$
such that
![]() $U_i=\theta _n^{-1}(U_i^n)$
. So, there is a partition of unity
$U_i=\theta _n^{-1}(U_i^n)$
. So, there is a partition of unity
![]() $\alpha _{\gamma _n}=\{h_i^n:i=1,\ldots ,k\}$
subordinated to
$\alpha _{\gamma _n}=\{h_i^n:i=1,\ldots ,k\}$
subordinated to
![]() $\gamma _n$
with
$\gamma _n$
with
![]() $\alpha _{\gamma _n}\subset E(Z_n)$
. Then,
$\alpha _{\gamma _n}\subset E(Z_n)$
. Then,
![]() $\{h^n_i\circ \theta _n:i=1,\ldots ,k\}$
is a partition of unity subordinated to
$\{h^n_i\circ \theta _n:i=1,\ldots ,k\}$
is a partition of unity subordinated to
![]() $\gamma $
and it is contained in
$\gamma $
and it is contained in
![]() $E(Z)$
. Finally, let
$E(Z)$
. Finally, let
![]() $\Psi =\{h\circ \triangle \Psi _0:h\in \Theta \}$
,
$\Psi =\{h\circ \triangle \Psi _0:h\in \Theta \}$
,
![]() $\overline \Psi =\{\overline f:f\in \Psi \}\subset C(\beta X,\overline {\mathbb R}),$
and
$\overline \Psi =\{\overline f:f\in \Psi \}\subset C(\beta X,\overline {\mathbb R}),$
and
![]() $\overline X_\Psi =(\triangle \overline \Psi )(\beta X)$
. Since C is a
$\overline X_\Psi =(\triangle \overline \Psi )(\beta X)$
. Since C is a
![]() $QS$
-algebra on Z, it separates the points and the closed sets in Z. Moreover,
$QS$
-algebra on Z, it separates the points and the closed sets in Z. Moreover,
![]() $C\subset E(Z)$
, which means that
$C\subset E(Z)$
, which means that
![]() $\overline X_\Psi $
is homeomorphic to Z.
$\overline X_\Psi $
is homeomorphic to Z.
Proof of Theorem 1.4
Let
![]() $T:C_p(X)\to C_p(Y)$
be a continuous linear surjection and
$T:C_p(X)\to C_p(Y)$
be a continuous linear surjection and
![]() $\dim X=0$
. To show that
$\dim X=0$
. To show that
![]() $\dim Y=0$
, it suffices to prove that for every
$\dim Y=0$
, it suffices to prove that for every
![]() $h\in \mathcal F_{Y}$
, there exists
$h\in \mathcal F_{Y}$
, there exists
![]() $h_0\in \mathcal F_{Y}$
with
$h_0\in \mathcal F_{Y}$
with
![]() $h_0\succ h$
and
$h_0\succ h$
and
![]() $\dim h_0(Y)=0$
. To this end, fix
$\dim h_0(Y)=0$
. To this end, fix
![]() $h\in \mathcal F_{Y}$
. Following the proof of Theorem 1.1 and using Lemmas 4.2 and 4.3, we are constructing two increasing sequences of countable sets
$h\in \mathcal F_{Y}$
. Following the proof of Theorem 1.1 and using Lemmas 4.2 and 4.3, we are constructing two increasing sequences of countable sets
![]() $\{\overline \Psi _n\}\subset C(\beta X,\overline {\mathbb R})$
,
$\{\overline \Psi _n\}\subset C(\beta X,\overline {\mathbb R})$
,
![]() $\{\overline \Phi _n\}\subset C(\beta Y,\overline {\mathbb R})$
, metrizable compactifications
$\{\overline \Phi _n\}\subset C(\beta Y,\overline {\mathbb R})$
, metrizable compactifications
![]() $\overline X_n=(\triangle \overline \Psi _n)(\beta X)$
and
$\overline X_n=(\triangle \overline \Psi _n)(\beta X)$
and
![]() $\overline Y_n=(\triangle \overline \Phi _n)(\beta Y)$
of the spaces
$\overline Y_n=(\triangle \overline \Phi _n)(\beta Y)$
of the spaces
![]() $X_n=(\triangle \Psi _n)(X)$
and
$X_n=(\triangle \Psi _n)(X)$
and
![]() $Y_n=(\triangle \Phi _n)(Y)$
, where
$Y_n=(\triangle \Phi _n)(Y)$
, where
![]() $\Psi _n=\overline \Psi _n|X$
and
$\Psi _n=\overline \Psi _n|X$
and
![]() $\Phi _n=\overline \Phi _n|Y$
, countable bases
$\Phi _n=\overline \Phi _n|Y$
, countable bases
![]() $\mathcal B_n'$
and
$\mathcal B_n'$
and
![]() $\mathcal B_n"$
for
$\mathcal B_n"$
for
![]() $\overline X_n$
and
$\overline X_n$
and
![]() $\overline Y_n$
and continuous surjections
$\overline Y_n$
and continuous surjections
![]() $\theta ^{n+1}_n:\overline X_{n+1}\to \overline X_n$
,
$\theta ^{n+1}_n:\overline X_{n+1}\to \overline X_n$
,
![]() $\delta ^{n+1}_n:\overline Y_{n+1}\to \overline Y_n$
satisfying the following conditions (everywhere below, if
$\delta ^{n+1}_n:\overline Y_{n+1}\to \overline Y_n$
satisfying the following conditions (everywhere below, if
![]() $f\in C(X)$
then
$f\in C(X)$
then
![]() $\overline f:\beta X\to \overline {\mathbb R}$
denotes its extension):
$\overline f:\beta X\to \overline {\mathbb R}$
denotes its extension):
-
(4.1)
 $\triangle \Phi _1\succ h$
,
$\triangle \Phi _1\succ h$
,
 $\Phi _n\subset \{T(f):f\in \Psi _{n}\}\subset \Phi _{n+1}$
and
$\Phi _n\subset \{T(f):f\in \Psi _{n}\}\subset \Phi _{n+1}$
and
 $\Psi _n\subset \Psi _{n+1}$
;
$\Psi _n\subset \Psi _{n+1}$
; -
(4.2) each
 $\pi _f$
,
$\pi _f$
,
 $f\in \Psi _n$
, is extendable to a map
$f\in \Psi _n$
, is extendable to a map
 $\overline \pi _f:\overline X_n\to \overline {\mathbb R}$
;
$\overline \pi _f:\overline X_n\to \overline {\mathbb R}$
; -
(4.3)
 $\Psi _n$
is admissible,
$\Psi _n$
is admissible,
 $\dim \overline X_n=0$
and
$\dim \overline X_n=0$
and
 $\mathcal B_n'$
satisfies condition (1) from Lemma 4.3;
$\mathcal B_n'$
satisfies condition (1) from Lemma 4.3; -
(4.4)
 $E(\overline X_n)=\{\overline \pi _f:f\in \Psi _n\}$
contains a countable
$E(\overline X_n)=\{\overline \pi _f:f\in \Psi _n\}$
contains a countable
 $QS$
-algebra
$QS$
-algebra
 $C_n\subset C(\overline X_n)$
on
$C_n\subset C(\overline X_n)$
on
 $\overline X_n$
such that
$\overline X_n$
such that
 $C_n$
satisfies condition (2) from the proof of Lemma 4.3;
$C_n$
satisfies condition (2) from the proof of Lemma 4.3; -
(4.5) for every finite open cover
 $\gamma $
of
$\gamma $
of
 $\overline X_n$
, consisting of sets from
$\overline X_n$
, consisting of sets from
 $\mathcal B_n'$
, there exists a partition of unity
$\mathcal B_n'$
, there exists a partition of unity
 $\alpha _\gamma $
subordinated to
$\alpha _\gamma $
subordinated to
 $\gamma $
with
$\gamma $
with
 $\alpha _\gamma \subset E(\overline X_n)$
;
$\alpha _\gamma \subset E(\overline X_n)$
; -
(4.6) every
 $\pi _g$
,
$\pi _g$
,
 $g\in \Phi _n$
, is extendable to a map
$g\in \Phi _n$
, is extendable to a map
 $\overline \pi _g:\overline Y_n\to \overline {\mathbb R}$
;
$\overline \pi _g:\overline Y_n\to \overline {\mathbb R}$
; -
(4.7)
 $\mathcal B_{n}"$
contains all inverse images
$\mathcal B_{n}"$
contains all inverse images
 $(\delta ^{n}_{n-1})^{-1}(U)$
,
$(\delta ^{n}_{n-1})^{-1}(U)$
,
 $U\in \mathcal B_{n-1}"$
, and is closed under finite intersections;
$U\in \mathcal B_{n-1}"$
, and is closed under finite intersections; -
(4.8) the set of real-valued functions from
 $E(\overline Y_n)=\{\overline \pi _g:g\in \Phi _n\}$
is dense in
$E(\overline Y_n)=\{\overline \pi _g:g\in \Phi _n\}$
is dense in
 $C_p(\overline Y_n)$
.
$C_p(\overline Y_n)$
.
Since
![]() $h(Y)$
is a separable metrizable space, there is a countable set
$h(Y)$
is a separable metrizable space, there is a countable set
![]() $\Phi _1'\subset C(Y)$
with
$\Phi _1'\subset C(Y)$
with
![]() ${h=\triangle \Phi _1'}$
. Let
${h=\triangle \Phi _1'}$
. Let
![]() $\overline {\Phi _1'}=\{\overline g:g\in \Phi ^{\prime }_1\}\subset C(\beta Y,\overline {\mathbb R})$
. By Lemma 4.2, there is a countable set
$\overline {\Phi _1'}=\{\overline g:g\in \Phi ^{\prime }_1\}\subset C(\beta Y,\overline {\mathbb R})$
. By Lemma 4.2, there is a countable set
![]() $\overline \Phi _1\subset C(\beta Y,\overline {\mathbb R})$
containing
$\overline \Phi _1\subset C(\beta Y,\overline {\mathbb R})$
containing
![]() $\overline {\Phi _1'}$
such that
$\overline {\Phi _1'}$
such that
![]() $(\triangle \overline \Phi _1)(\beta Y)$
is homeomorphic to
$(\triangle \overline \Phi _1)(\beta Y)$
is homeomorphic to
![]() $(\triangle \overline {\Phi _1'})(\beta Y)$
and
$(\triangle \overline {\Phi _1'})(\beta Y)$
and
![]() $\{\pi _{\overline g}:\overline g\in \overline \Phi _1\}$
contains a dense subset of
$\{\pi _{\overline g}:\overline g\in \overline \Phi _1\}$
contains a dense subset of
![]() $C_p(\overline Y_1)$
, where
$C_p(\overline Y_1)$
, where
![]() $\overline Y_1=(\triangle \overline \Phi _1)(\beta Y)$
. Let
$\overline Y_1=(\triangle \overline \Phi _1)(\beta Y)$
. Let
![]() $\Phi _1=\{g:\overline g\in \overline \Phi _1\}$
,
$\Phi _1=\{g:\overline g\in \overline \Phi _1\}$
,
![]() $Y_1=(\triangle \Phi _1)(Y),$
and
$Y_1=(\triangle \Phi _1)(Y),$
and
![]() $E(\overline Y_1)=\{\overline \pi _{g}:g\in \Phi _1\}$
. So,
$E(\overline Y_1)=\{\overline \pi _{g}:g\in \Phi _1\}$
. So,
![]() $\Phi _1$
satisfies conditions (4.6) and (4.7). Next, choose a countable set
$\Phi _1$
satisfies conditions (4.6) and (4.7). Next, choose a countable set
![]() $\Psi _1'\subset C(X)$
with
$\Psi _1'\subset C(X)$
with
![]() $T(\Psi _1')=\Phi _1$
and apply Lemma 4.3 to find a countable admissible set
$T(\Psi _1')=\Phi _1$
and apply Lemma 4.3 to find a countable admissible set
![]() $\Psi _1$
containing
$\Psi _1$
containing
![]() $\Psi _1'$
and a metrizable compactification
$\Psi _1'$
and a metrizable compactification
![]() $\overline X_1$
of
$\overline X_1$
of
![]() $X_1=\triangle \Psi _1(X)$
satisfying conditions (4.2)–(4.5).
$X_1=\triangle \Psi _1(X)$
satisfying conditions (4.2)–(4.5).
Suppose the construction is done for all
![]() $k\leq n$
. Let
$k\leq n$
. Let
![]() $\Phi _{n+1}'\subset C(Y)$
be a countable set containing
$\Phi _{n+1}'\subset C(Y)$
be a countable set containing
![]() $T(\Psi _n)$
and denote
$T(\Psi _n)$
and denote
![]() $\overline {\Phi '}_{n+1}=\{\overline g:g\in \Phi ^{\prime }_{n+1}\}\subset C(\beta Y,\overline {\mathbb R})$
. By Lemma 4.2, there is a countable set
$\overline {\Phi '}_{n+1}=\{\overline g:g\in \Phi ^{\prime }_{n+1}\}\subset C(\beta Y,\overline {\mathbb R})$
. By Lemma 4.2, there is a countable set
![]() $\overline \Phi _{n+1}\subset C(\beta Y,\overline {\mathbb R})$
containing
$\overline \Phi _{n+1}\subset C(\beta Y,\overline {\mathbb R})$
containing
![]() $\overline {\Phi '}_{n+1}$
such that
$\overline {\Phi '}_{n+1}$
such that
![]() $(\triangle \overline \Phi _{n+1})(\beta Y)$
is homeomorphic to
$(\triangle \overline \Phi _{n+1})(\beta Y)$
is homeomorphic to
![]() $(\triangle \overline {\Phi '}_{n+1})(\beta Y)$
and
$(\triangle \overline {\Phi '}_{n+1})(\beta Y)$
and
![]() $\{\pi _{\overline g}:\overline g\in \overline \Phi _{n+1}\}$
contains a dense subset of
$\{\pi _{\overline g}:\overline g\in \overline \Phi _{n+1}\}$
contains a dense subset of
![]() $C_p(\overline Y_{n+1})$
, where
$C_p(\overline Y_{n+1})$
, where
![]() $\overline Y_{n+1}=(\triangle \overline \Phi _{n+1})(\beta Y)$
. Let
$\overline Y_{n+1}=(\triangle \overline \Phi _{n+1})(\beta Y)$
. Let
![]() $\Phi _{n+1}=\{g:\overline g\in \overline \Phi _{n+1}\}$
and
$\Phi _{n+1}=\{g:\overline g\in \overline \Phi _{n+1}\}$
and
![]() $Y_{n+1}=(\triangle \Phi _{n+1})(Y)$
. Note that
$Y_{n+1}=(\triangle \Phi _{n+1})(Y)$
. Note that
![]() $\Phi _n\subset \Phi _{n+1}$
because
$\Phi _n\subset \Phi _{n+1}$
because
![]() $\Phi _n\subset T(\Psi _n)$
. Next, choose a countable set
$\Phi _n\subset T(\Psi _n)$
. Next, choose a countable set
![]() $\Psi _{n+1}'\subset C(X)$
with
$\Psi _{n+1}'\subset C(X)$
with
![]() $T(\Psi _{n+1}')=\Phi _{n+1}$
and apply Lemma 4.3 to find a countable admissible set
$T(\Psi _{n+1}')=\Phi _{n+1}$
and apply Lemma 4.3 to find a countable admissible set
![]() $\Psi _{n+1}$
containing
$\Psi _{n+1}$
containing
![]() $\Psi _{n+1}'\cup \Psi _n$
and a metrizable compactification
$\Psi _{n+1}'\cup \Psi _n$
and a metrizable compactification
![]() $\overline X_{n+1}$
of
$\overline X_{n+1}$
of
![]() $X_{n+1}=(\triangle \Psi _{n+1})(X)$
satisfying conditions (4.1)–(4.5). Because
$X_{n+1}=(\triangle \Psi _{n+1})(X)$
satisfying conditions (4.1)–(4.5). Because
![]() $\overline \Psi _n\subset \overline \Psi _{n+1}$
,
$\overline \Psi _n\subset \overline \Psi _{n+1}$
,
![]() $\triangle \overline \Psi _{n+1}\succ \triangle \overline \Psi _{n}$
. Hence, there exists a map
$\triangle \overline \Psi _{n+1}\succ \triangle \overline \Psi _{n}$
. Hence, there exists a map
![]() $\theta ^{n+1}_n:\overline X_{n+1}\to \overline X_n$
defined by
$\theta ^{n+1}_n:\overline X_{n+1}\to \overline X_n$
defined by
![]() $\theta ^{n+1}_n=\triangle \overline \Psi _{n}((\triangle \overline \Psi _{n+1})^{-1}(x))$
. This completes the induction.
$\theta ^{n+1}_n=\triangle \overline \Psi _{n}((\triangle \overline \Psi _{n+1})^{-1}(x))$
. This completes the induction.
As in the proof of Theorem 1.1, we denote
![]() $\overline X_0=(\triangle \overline \Psi )(\beta X)$
,
$\overline X_0=(\triangle \overline \Psi )(\beta X)$
,
![]() $\overline Y_0=(\triangle \overline \Phi )(\beta Y),$
and
$\overline Y_0=(\triangle \overline \Phi )(\beta Y),$
and
![]() $h_0=\triangle \Phi $
, where
$h_0=\triangle \Phi $
, where
![]() $\Psi =\bigcup _n\Psi _n$
and
$\Psi =\bigcup _n\Psi _n$
and
![]() $\Phi =\bigcup _n\Phi _n$
. Clearly,
$\Phi =\bigcup _n\Phi _n$
. Clearly,
![]() $\Phi =\{T(f): f\in \Psi \}$
. Since
$\Phi =\{T(f): f\in \Psi \}$
. Since
![]() $\overline X_0$
is the limit space of the inverse sequence
$\overline X_0$
is the limit space of the inverse sequence
![]() $S_X=\{\overline X_n,\theta ^{n+1}_n\}$
and
$S_X=\{\overline X_n,\theta ^{n+1}_n\}$
and
![]() $\dim \overline X_n=0$
for all n,
$\dim \overline X_n=0$
for all n,
![]() $\dim \overline X_0=0$
. Moreover,
$\dim \overline X_0=0$
. Moreover,
![]() $E(X_0)=\{\pi _f:f\in \Psi \}$
is a countable
$E(X_0)=\{\pi _f:f\in \Psi \}$
is a countable
![]() $QS$
-algebra on
$QS$
-algebra on
![]() $X_0$
such that every
$X_0$
such that every
![]() $\pi _f$
is extendable to a continuous map
$\pi _f$
is extendable to a continuous map
![]() $\overline \pi _f:\overline X_0\to \overline {\mathbb R}$
. Denote
$\overline \pi _f:\overline X_0\to \overline {\mathbb R}$
. Denote
![]() $E(\overline X_0)=\{\overline \pi _f:f\in \Psi \}$
. Let also
$E(\overline X_0)=\{\overline \pi _f:f\in \Psi \}$
. Let also
![]() $C=\bigcup _n\{h\circ \theta _n:h\in C_n\}\subset E(\overline X_0)$
. The same arguments as in the proof of Lemma 4.3 show that C is a
$C=\bigcup _n\{h\circ \theta _n:h\in C_n\}\subset E(\overline X_0)$
. The same arguments as in the proof of Lemma 4.3 show that C is a
![]() $QS$
-algebra on
$QS$
-algebra on
![]() $\overline X_0$
satisfying condition (2.3). Let
$\overline X_0$
satisfying condition (2.3). Let
![]() $\mathcal B'$
be the base of
$\mathcal B'$
be the base of
![]() $\overline X_0$
generated by the bases
$\overline X_0$
generated by the bases
![]() $\mathcal B_n'$
. The arguments from the proof of Lemma 4.3 also provide that for every finite open cover
$\mathcal B_n'$
. The arguments from the proof of Lemma 4.3 also provide that for every finite open cover
![]() $\gamma $
of
$\gamma $
of
![]() $\overline X_0$
, consisting of open sets from
$\overline X_0$
, consisting of open sets from
![]() $\mathcal B'$
there exists a partition of unity
$\mathcal B'$
there exists a partition of unity
![]() $\alpha _\gamma $
subordinated to
$\alpha _\gamma $
subordinated to
![]() $\gamma $
with
$\gamma $
with
![]() $\alpha _\gamma \subset E(\overline X_0)$
.
$\alpha _\gamma \subset E(\overline X_0)$
.
Because
![]() $\Phi _n\subset \Phi _{n+1}$
,
$\Phi _n\subset \Phi _{n+1}$
,
![]() $\overline \Phi _n\subset \overline \Phi _{n+1}$
. This implies
$\overline \Phi _n\subset \overline \Phi _{n+1}$
. This implies
![]() $\triangle \Phi _{n+1}\succ \triangle \Phi _{n}$
. So, for every
$\triangle \Phi _{n+1}\succ \triangle \Phi _{n}$
. So, for every
![]() $n,$
there is map
$n,$
there is map
![]() $\delta ^{n+1}_n:\overline Y_{n+1}\to \overline Y_n$
defined by
$\delta ^{n+1}_n:\overline Y_{n+1}\to \overline Y_n$
defined by
![]() $\delta ^{n+1}_n(y)=\triangle \Phi _{n}((\triangle \Phi _{n+1})^{-1}(y))$
. Then,
$\delta ^{n+1}_n(y)=\triangle \Phi _{n}((\triangle \Phi _{n+1})^{-1}(y))$
. Then,
![]() $\overline Y_0$
is the limit of the inverse sequence
$\overline Y_0$
is the limit of the inverse sequence
![]() $S_Y=\{\overline Y_n,\delta ^{n+1}_n\}$
. Let
$S_Y=\{\overline Y_n,\delta ^{n+1}_n\}$
. Let
![]() $E(Y_0)=\{\pi _g:g\in \Phi \}$
and
$E(Y_0)=\{\pi _g:g\in \Phi \}$
and
![]() $E(\overline Y_0)=\{\overline \pi _{g}:g\in \Phi \}$
. We claim that the set of real-valued elements of
$E(\overline Y_0)=\{\overline \pi _{g}:g\in \Phi \}$
. We claim that the set of real-valued elements of
![]() $E_p(\overline Y_0)$
is dense in
$E_p(\overline Y_0)$
is dense in
![]() $C_p(\overline Y_0)$
. Indeed, every projection
$C_p(\overline Y_0)$
. Indeed, every projection
![]() $\delta _n:\overline Y_0\to \overline Y_n$
induces a continuous map
$\delta _n:\overline Y_0\to \overline Y_n$
induces a continuous map
![]() $\delta _n^*:C_p(\overline Y_n)\to C_p(\overline Y_0)$
defined by
$\delta _n^*:C_p(\overline Y_n)\to C_p(\overline Y_0)$
defined by
![]() $\delta _n^*(h)=h\circ \delta _n$
. Because the set of real-valued functions from
$\delta _n^*(h)=h\circ \delta _n$
. Because the set of real-valued functions from
![]() $E(\overline Y_n)=\{\overline \pi _{g}:g\in \Phi _n\}$
is dense in
$E(\overline Y_n)=\{\overline \pi _{g}:g\in \Phi _n\}$
is dense in
![]() $C_p(\overline Y_n)$
and
$C_p(\overline Y_n)$
and
![]() $E_p(\overline Y_0)=\bigcup _n\delta _n^*(E(\overline Y_n))$
, it suffices to show that
$E_p(\overline Y_0)=\bigcup _n\delta _n^*(E(\overline Y_n))$
, it suffices to show that
![]() $\bigcup _n\delta _n^*(C_p(\overline Y_n))$
is dense in
$\bigcup _n\delta _n^*(C_p(\overline Y_n))$
is dense in
![]() $C_p(\overline Y_0)$
. To this end, let
$C_p(\overline Y_0)$
. To this end, let
![]() $O=\{f\in C_p(\overline Y_0):|f(\overline y_i)-f_0(\overline y_i)|<\varepsilon _i, i=1,\ldots ,k\}$
be a neighborhood of some
$O=\{f\in C_p(\overline Y_0):|f(\overline y_i)-f_0(\overline y_i)|<\varepsilon _i, i=1,\ldots ,k\}$
be a neighborhood of some
![]() $f_0\in C_p(\overline Y_0)$
, where all
$f_0\in C_p(\overline Y_0)$
, where all
![]() $\overline y_i$
are different points from
$\overline y_i$
are different points from
![]() $\overline Y_0$
. Since the base
$\overline Y_0$
. Since the base
![]() $\mathcal B"$
of
$\mathcal B"$
of
![]() $\overline Y_0$
consists of all sets of the form
$\overline Y_0$
consists of all sets of the form
![]() $\delta _n^{-1}(U_n)$
,
$\delta _n^{-1}(U_n)$
,
![]() $U_n\in \mathcal B_n"$
, there is n and different points
$U_n\in \mathcal B_n"$
, there is n and different points
![]() $y_i\in \overline Y_n$
such that
$y_i\in \overline Y_n$
such that
![]() $\delta _n(\overline y_i)=y_i$
and
$\delta _n(\overline y_i)=y_i$
and
![]() $\delta _n^{-1}(U_i)\subset f_0^{-1}(V_i)$
, where
$\delta _n^{-1}(U_i)\subset f_0^{-1}(V_i)$
, where
![]() $U_i\in \mathcal B_n"$
and
$U_i\in \mathcal B_n"$
and
![]() $V_i$
is the open interval
$V_i$
is the open interval
![]() $(f_0(\overline y_i)-\varepsilon _i,f_0(\overline y_i)+\varepsilon _i)$
. Then, the set
$(f_0(\overline y_i)-\varepsilon _i,f_0(\overline y_i)+\varepsilon _i)$
. Then, the set
![]() $W=\{h\in C_p(\overline Y_n):h(y_i)\in V_i, i=1,2,\ldots ,k\}$
is open in
$W=\{h\in C_p(\overline Y_n):h(y_i)\in V_i, i=1,2,\ldots ,k\}$
is open in
![]() $C_p(\overline Y_n)$
. So, it contains a function
$C_p(\overline Y_n)$
. So, it contains a function
![]() $h_0\in E(\overline Y_n)$
. Hence,
$h_0\in E(\overline Y_n)$
. Hence,
![]() $h_0\circ \delta _n$
is a function from
$h_0\circ \delta _n$
is a function from
![]() $\bigcup _n\delta _n^*(C_p(\overline Y_n))\cap O$
. So, the set of all real-valued functions from
$\bigcup _n\delta _n^*(C_p(\overline Y_n))\cap O$
. So, the set of all real-valued functions from
![]() $E(\overline Y_0)$
is dense in
$E(\overline Y_0)$
is dense in
![]() $C_p(\overline Y_0)$
.
$C_p(\overline Y_0)$
.
Because T is linear, so is the map
![]() $\varphi :E_p(X_0)\to E_p(Y_0)$
defined by
$\varphi :E_p(X_0)\to E_p(Y_0)$
defined by
![]() $\varphi (\pi _f)=\pi _{T(f)}$
. The arguments from the proof of Theorem 1.1 show that
$\varphi (\pi _f)=\pi _{T(f)}$
. The arguments from the proof of Theorem 1.1 show that
![]() $\varphi $
is continuous, but we are going to prove the more general fact that
$\varphi $
is continuous, but we are going to prove the more general fact that
![]() $\varphi $
has a continuous extension over the linear hull
$\varphi $
has a continuous extension over the linear hull
![]() $LE_p(X_0)$
. For every
$LE_p(X_0)$
. For every
![]() $f\in LE(X_0),$
let
$f\in LE(X_0),$
let
![]() $f^*=f\circ (\triangle \Psi )\in C(X)$
. Evidently, if
$f^*=f\circ (\triangle \Psi )\in C(X)$
. Evidently, if
![]() $f=\sum _{i=1}^k\lambda _i\cdot f_i\in LE(X_0)$
, then
$f=\sum _{i=1}^k\lambda _i\cdot f_i\in LE(X_0)$
, then
![]() $f^*=\sum _{i=1}^k\lambda _i\cdot f_i^*$
. So, we have another description of the map
$f^*=\sum _{i=1}^k\lambda _i\cdot f_i^*$
. So, we have another description of the map
![]() $\varphi $
:
$\varphi $
:
![]() $\varphi (f)=\pi _{T(f^*)}$
,
$\varphi (f)=\pi _{T(f^*)}$
,
![]() $f\in E(X_0)$
.
$f\in E(X_0)$
.
Claim 17 Let
![]() $f=\sum _{i=1}^k\lambda _i\cdot f_i\in LE(X_0)$
with
$f=\sum _{i=1}^k\lambda _i\cdot f_i\in LE(X_0)$
with
![]() $f_i\in E(X_0)$
for all i. If
$f_i\in E(X_0)$
for all i. If
![]() $y^*\in Y$
and
$y^*\in Y$
and
![]() $(\triangle \Phi )(y^*)=y$
, then
$(\triangle \Phi )(y^*)=y$
, then
![]() $T(f^*)(y^*)=\sum _{i=1}^k\lambda _i\cdot T(f_i^*)(y^*)=\sum _{i=1}^k\lambda _i\cdot \varphi (f_i)(y)$
.
$T(f^*)(y^*)=\sum _{i=1}^k\lambda _i\cdot T(f_i^*)(y^*)=\sum _{i=1}^k\lambda _i\cdot \varphi (f_i)(y)$
.
It suffices to show that
![]() $T(f^*)(y^*)=\varphi (f)(y)$
for all
$T(f^*)(y^*)=\varphi (f)(y)$
for all
![]() $f\in E(X_0)$
. And that is true because
$f\in E(X_0)$
. And that is true because
![]() $f^*\in \Psi $
, so
$f^*\in \Psi $
, so
![]() $T(f^*)\in \Phi $
and
$T(f^*)\in \Phi $
and
![]() $T(f^*)(y^*)=\varphi (f)(y)$
.
$T(f^*)(y^*)=\varphi (f)(y)$
.
We define
![]() $\widetilde \varphi :LE(X_0)\to LE(Y_0)$
by
$\widetilde \varphi :LE(X_0)\to LE(Y_0)$
by
![]() $\widetilde \varphi (\sum _{i=1}^k\lambda _i\cdot f_i)=\sum _{i=1}^k\lambda _i\cdot \varphi (f_i)$
, where
$\widetilde \varphi (\sum _{i=1}^k\lambda _i\cdot f_i)=\sum _{i=1}^k\lambda _i\cdot \varphi (f_i)$
, where
![]() $\lambda _i\in \mathbb R$
and
$\lambda _i\in \mathbb R$
and
![]() $f_i\in E(X_0)$
. The continuity of
$f_i\in E(X_0)$
. The continuity of
![]() $\widetilde \varphi $
with respect to the pointwise topology is equivalent of the continuity of all linear functionals
$\widetilde \varphi $
with respect to the pointwise topology is equivalent of the continuity of all linear functionals
![]() $\widetilde l_y:LE_p(X_0)\to \mathbb R$
defined by
$\widetilde l_y:LE_p(X_0)\to \mathbb R$
defined by
![]() $\widetilde l_y(f)=\widetilde \varphi (f)(y)$
,
$\widetilde l_y(f)=\widetilde \varphi (f)(y)$
,
![]() $y\in Y_0$
. So, fix
$y\in Y_0$
. So, fix
![]() $y_0\in Y_0$
and
$y_0\in Y_0$
and
![]() $f_0=\sum _{i=1}^k\lambda _i\cdot f_i\in LE(X_0)$
with
$f_0=\sum _{i=1}^k\lambda _i\cdot f_i\in LE(X_0)$
with
![]() $f_i\in E(X_0)$
such that
$f_i\in E(X_0)$
such that
![]() $\widetilde l_{y_0}(f_0)\in V$
for some open interval
$\widetilde l_{y_0}(f_0)\in V$
for some open interval
![]() $V\subset \mathbb R$
. Then,
$V\subset \mathbb R$
. Then,
![]() $f_0^*=\sum _{i=1}^k\lambda _i\cdot f_i^*$
and, by Claim 17, we have
$f_0^*=\sum _{i=1}^k\lambda _i\cdot f_i^*$
and, by Claim 17, we have
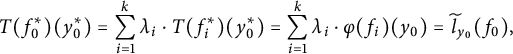 $$ \begin{align*}T(f_0^*)(y_0^*)=\sum_{i=1}^k\lambda_i\cdot T(f_i^*)(y_0^*)=\sum_{i=1}^k\lambda_i\cdot\varphi(f_i)(y_0)=\widetilde l_{y_0}(f_0),\end{align*} $$
$$ \begin{align*}T(f_0^*)(y_0^*)=\sum_{i=1}^k\lambda_i\cdot T(f_i^*)(y_0^*)=\sum_{i=1}^k\lambda_i\cdot\varphi(f_i)(y_0)=\widetilde l_{y_0}(f_0),\end{align*} $$
where
![]() $y_0^*\in Y$
with
$y_0^*\in Y$
with
![]() $(\triangle \Phi )(y_0^*)=y_0$
. Consequently, there is a neighborhood
$(\triangle \Phi )(y_0^*)=y_0$
. Consequently, there is a neighborhood
![]() $W^*=\{g\in C_p(X):|g(x_j^*)-f_0^*(x_j^*)|<\eta _j, j=1,2,\ldots ,m\}$
of
$W^*=\{g\in C_p(X):|g(x_j^*)-f_0^*(x_j^*)|<\eta _j, j=1,2,\ldots ,m\}$
of
![]() $f_0^*$
in
$f_0^*$
in
![]() $C_p(X)$
such that
$C_p(X)$
such that
![]() $T(g)(y_0^*)\in V$
for all
$T(g)(y_0^*)\in V$
for all
![]() $g\in W^*$
. Observe that
$g\in W^*$
. Observe that
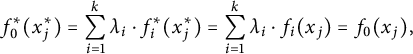 $$ \begin{align*}f_0^*(x_j^*)=\sum_{i=1}^k\lambda_i\cdot f_i^*(x_j^*)=\sum_{i=1}^k\lambda_i\cdot f_i(x_j)=f_0(x_j),\end{align*} $$
$$ \begin{align*}f_0^*(x_j^*)=\sum_{i=1}^k\lambda_i\cdot f_i^*(x_j^*)=\sum_{i=1}^k\lambda_i\cdot f_i(x_j)=f_0(x_j),\end{align*} $$
where
![]() $x_j=(\triangle \Psi )(x_j^*)$
. So,
$x_j=(\triangle \Psi )(x_j^*)$
. So,
![]() $W=\{f\in LE(X_0):|f(x_j)-f_0(x_j)|<\eta _j,j=1,2,\ldots ,m\}$
is a neighborhood of
$W=\{f\in LE(X_0):|f(x_j)-f_0(x_j)|<\eta _j,j=1,2,\ldots ,m\}$
is a neighborhood of
![]() $f_0$
in
$f_0$
in
![]() $LE_p(X_0)$
. If
$LE_p(X_0)$
. If
![]() $g\in W$
, then
$g\in W$
, then
![]() $g=\sum _{s=1}^m\lambda _s\cdot g_s$
for some
$g=\sum _{s=1}^m\lambda _s\cdot g_s$
for some
![]() ${g_s\in E(X_0)}$
. Hence,
${g_s\in E(X_0)}$
. Hence,
![]() $g^*=\sum _{s=1}^m\lambda _s\cdot g_s^*\in W^*$
, which means that
$g^*=\sum _{s=1}^m\lambda _s\cdot g_s^*\in W^*$
, which means that
![]() $T(g^*)(y_0^*)\in V$
. Finally, according to Claim 17,
$T(g^*)(y_0^*)\in V$
. Finally, according to Claim 17,
![]() $T(g^*)(y_0^*)=\sum _{s=1}^m\lambda _s\cdot \varphi (g_s)(y_0)=\widetilde l_{y_0}(g)\in V$
. Thus,
$T(g^*)(y_0^*)=\sum _{s=1}^m\lambda _s\cdot \varphi (g_s)(y_0)=\widetilde l_{y_0}(g)\in V$
. Thus,
![]() $\widetilde \varphi :LE_p(X_0)\to LE_p(Y_0)$
is continuous.
$\widetilde \varphi :LE_p(X_0)\to LE_p(Y_0)$
is continuous.
Therefore, the spaces
![]() $X_0$
,
$X_0$
,
![]() $\overline X_0$
,
$\overline X_0$
,
![]() $Y_0$
, and
$Y_0$
, and
![]() $\overline Y_0$
satisfy the assumptions of Proposition 4.1. So, we apply Proposition 4.1 with
$\overline Y_0$
satisfy the assumptions of Proposition 4.1. So, we apply Proposition 4.1 with
![]() $X=X_0$
and
$X=X_0$
and
![]() $Y=Y_0$
to conclude that
$Y=Y_0$
to conclude that
![]() $\dim Y_0=0$
. That completes the proof of Theorem 1.4.
$\dim Y_0=0$
. That completes the proof of Theorem 1.4.
Acknowledgements
The authors express their gratitude to referees for their many suggestions and improvements.