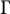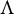1 Introduction
Let
$\Gamma $
and
$\Lambda $
be two countable discrete groups with free probability measure-preserving actions
$\Gamma {\, \curvearrowright \,} (X,\mu )$
and
$\Lambda {\, \curvearrowright \,}(Y,\nu )$
on standard probability measure spaces
$(X,\mu )$
and
$(Y,\nu )$
, respectively. An orbit equivalence (OE) for the actions is a measurable isomorphism
$\theta :X\to Y$
such that
$\theta (\Gamma x)=\Lambda \theta (x)$
for almost every
$x\in X$
. In this case, the two actions are called orbit equivalent. Two groups are said to be orbit equivalent if they admit orbit equivalent actions. Singer [Reference SingerSin55] showed that for two free probability measure-preserving actions
$\Gamma {\, \curvearrowright \,}(X,\mu )$
and
$\Lambda {\, \curvearrowright \,}(Y,\nu )$
, being orbit equivalent is equivalent to the existence of an isomorphism
$L^\infty (X)\rtimes \Gamma \cong L^\infty (Y)\rtimes \Lambda $
which preserves the Cartan subalgebras
$L^\infty (X)$
and
$L^\infty (Y)$
. OE theory saw some development in the 1980s (see [Reference Connes, Feldman and WeissCFW81, Reference Ornstein and WeissOW80, Reference ZimmerZim84]), and has been an area of active research over the last two decades (see [Reference FurmanFur11, Reference GaboriauGab10]). These advances in part have been stimulated by the success of the deformation/rigidity theory approach to the classification of
$\mathrm {II}_1$
factors developed by Popa and others (see [Reference IoanaIoa13, Reference PopaPop08, Reference VaesVae10]).
The study of OE can also be motivated from an entirely different point of view, being a measurable counterpart to quasi-isometry of groups. Gromov [Reference GromovGro93] introduced measure equivalence (ME) for countable discrete groups as a measurable analog of quasi-isometry and since then, this notion has proven to be an important tool in geometric group theory with connections to ergodic theory and operator algebras. Two infinite countable discrete groups
$\Gamma $
and
$\Lambda $
are measure equivalent if there is a standard infinite measure space
$(\Omega ,m)$
with commuting, measure-preserving actions
$\Gamma {\, \curvearrowright \,}(\Omega ,m)$
and
$\Lambda {\, \curvearrowright \,}(\Omega ,m)$
, so that both the actions admit finite-measure fundamental domains
$Y,X\in \Omega $
, that is,
$m(Y),m(X)<\infty $
and
$$ \begin{align*}\Omega=\bigsqcup_{\gamma\in\Gamma}\gamma Y=\bigsqcup_{\lambda\in\Lambda}\lambda X.\end{align*} $$
The space
$(\Omega ,m)$
is called an ME-coupling between
$\Gamma $
and
$\Lambda $
, and the index of such a coupling is
$$ \begin{align*}[\Gamma:\Lambda]_\Omega:=\frac{m(X)}{m(Y)}.\end{align*} $$
Notably, ME was used by Furman in [Reference FurmanFur99a, Reference FurmanFur99b] to prove strong rigidity results for lattices in higher rank simple Lie groups. ME relates back to OE because of the following fact, observed by Zimmer and Furman: for two discrete groups
$\Gamma $
and
$\Lambda $
, admitting free OE actions is equivalent to having an ME-coupling so that the fundamental domains coincide (see, for example, [Reference GaboriauGab05, P
${}_{\rm ME}$
5] and [Reference FurmanFur11, Theorem 2.5]).
If
$X \subset \Omega $
is a Borel fundamental domain for the action
$\Gamma {\, \curvearrowright \,}(\Omega ,m)$
, then on the level of function spaces, the characteristic function
$1_X$
gives a projection in
$L^\infty (\Omega , m)$
such that the collection
$\{ 1_{\gamma X} \}_{\gamma \in \Gamma }$
forms a partition of unity, i.e.,
$\sum _{\gamma \in \Gamma } 1_{\gamma X} = 1$
. This notion generalizes quite nicely to the non-commutative setting, and using this, Peterson, Ruth, and the first named author, in [Reference Ishan, Peterson and RuthIPR24], defined that a fundamental domain for an action on a von Neumann algebra
$\Gamma {\, \curvearrowright ^{\sigma } \,} \mathcal M$
is a projection
$p \in \mathcal M$
such that
$\sum _{\gamma \in \Gamma }\sigma _\gamma (p) = 1$
, where the convergence is in the strong operator topology. Using this perspective for a fundamental domain, they generalized the notion of ME by considering actions on non-commutative spaces.
Definition 1.1 [Reference Ishan, Peterson and RuthIPR24]
Two countable discrete groups
$\Gamma $
and
$\Lambda $
are von Neumann equivalent (vNE), written
$\Gamma \sim _{\mathrm {vNE}} \Lambda $
, if there exists a von Neumann algebra
$\mathcal M$
with a faithful normal semi-finite trace
$\mathrm {Tr}$
and commuting, trace-preserving actions of
$\Gamma $
and
$\Lambda $
on
$\mathcal M$
such that the
$\Gamma $
- and
$\Lambda $
-actions individually admit a finite-trace fundamental domain. The semi-finite von Neumann algebra
$\mathcal {M}$
is called a von Neumann coupling between
$\Gamma $
and
$\Lambda $
.
Like ME, vNE is stable under taking the direct product of groups. But neither ME nor vNE is stable under taking free products. For instance, since any two finite groups are ME (and hence vNE), and amenability is preserved under both ME and vNE, one gets that
$\mathbb Z/2\mathbb Z*\mathbb Z/2\mathbb Z$
(amenable) is neither ME nor vNE to
$\mathbb Z/3\mathbb Z*\mathbb Z/2\mathbb Z$
(non-amenable). However, as suggested in [Reference Monod and ShalomMS06, Remark 2.28], and proved in [Reference GaboriauGab05, P
ME
6], stability under taking free products hold if one requires the additional assumption that groups are ME with a common fundamental domain. In other words, OE is stable under taking free products. This raises a natural question: Is vNE, with common fundamental domain, stable under taking free products? We obtain an affirmative answer to this question and introduce the following definition.
Definition 1.2 Two countable discrete groups
$\Gamma $
and
$\Lambda $
are said to be von Neumann orbit equivalent (vNOE), denoted
$\Gamma \sim _{\mathrm {vNOE}}\Lambda $
, if there exists a von Neumann coupling between
$\Gamma $
and
$\Lambda $
with a common fundamental domain.
Theorem 1.3 If
$\Gamma _i,\Lambda _i, ~i=1,2$
are countable discrete groups such that
$\Gamma _i\sim _{\mathrm {vNOE}}\Lambda _i, ~i=1,2$
, then
$\Gamma _1*\Gamma _2\sim _{\mathrm {vNOE}}\Lambda _1*\Lambda _2$
.
Green [Reference GreenGre90], in her Ph.D. thesis, introduced graph products of groups, another important group-theoretical construction. If
$\mathcal {G}=(V,E)$
is a simple, non-oriented graph with vertex set V and edge set E, then the graph product of a family,
$\{\Gamma _v\}_{v\in V}$
, of groups indexed by V is obtained from the free product
$*_{v\in V}\Gamma _v$
by adding commutator relations determined by the edge set E. Depending on the graph, free products and direct products are special cases of the graph product construction. Adapting the ideas of [Reference GaboriauGab05], Horbez and Huang [Reference Horbez and HuangHH22, Proposition 4.2] proved the stability of OE under taking graph products over finite simple graphs (see also [Reference DemirDem22]). To further explore the study of graph products within the context of measured group theory, we would like to draw the reader’s attention to the article [Reference Escalier and HorbezEH24]. In the current article, we also prove the stability of vNOE under taking graph products.
Theorem 1.4 Let
$\mathcal {G}=(V,E)$
be a simple graph with at most countably infinite vertices. Let
$\Gamma $
and
$\Lambda $
be two graph products over
$\mathcal {G}$
, with countable vertex groups
$\{\Gamma _v\}_{v\in V}$
and
$\{\Lambda _v\}_{v\in V}$
, respectively. If
$\Gamma _v\sim _{\mathrm {vNOE}}\Lambda _v$
for every
$v\in V$
, then
$\Gamma \sim _{\mathrm {vNOE}}\Lambda $
.
In attempting to prove the above theorems, if one tries to adapt the techniques from one of [Reference GaboriauGab05, Reference Horbez and HuangHH22, Reference DemirDem22], an immediate problem is presented by the lack of “point perspective” in the theory of von Neumann (orbit) equivalence. The lack of any natural non-commutative analog of the notion of OE/ME cocycles, or that of measured equivalence relation, can be considered as a few problems presented by the lack of point perspective. This often leads one to consider genuinely new techniques and different alternatives (see, e.g., [Reference BattserenBat23a, Reference BattserenBat23b, Reference Ishan, Peterson and RuthIPR24, Reference IshanIsh24]). To overcome this obstruction, we introduce the notion of vNOE for tracial von Neumann algebras that is “compatible” with vNOE of groups (see Definition 1.5 and Theorem 3.11), and prove the analogs of Theorems 1.3 and 1.4 at the level of tracial von Neumann algebras.
The notion of von Neumann equivalence admits a generalization in the setting of finite von Neumann algebras [Reference Ishan, Peterson and RuthIPR24, Section 8], and relates to vNE for groups as follows:
$\Gamma \sim _{\mathrm {vNE}}\Lambda $
if and only if
$L\Gamma \sim _{\mathrm {vNE}}L\Lambda $
[Reference Ishan, Peterson and RuthIPR24, Theorem 1.5]. In parallel to this, one might attempt to define two tracial von Neumann algebras to be vNOE if they are vNE and admit a “common” fundamental domain, and identify a correct meaning of “common.” However, we take a slightly different approach, and motivated by the recently defined notion of ME of finite von Neumann algebras by Berendschot and Vaes in [Reference Berendschot and VaesBV25], we introduce the following definition.
Definition 1.5 Let
$(A,\tau _A)$
and
$(B,\tau _B)$
be tracial von Neumann algebras. We say that
$(A,\tau _A)$
and
$(B,\tau _B)$
are vNOE, denoted
$(A,\tau _A)\sim _{\mathrm {vNOE}}(B,\tau _B)$
, if there exists a tracial von Neumann algebra
$(Q,\tau _Q)$
, a Hilbert
$A\, \overline {\otimes }\, Q-B$
-bimodule
$\mathcal H$
, and a vector
$\xi \in \mathcal H$
such that:
-
(1)
$\langle (a\otimes x)\xi ,\xi \rangle =\tau _A(a)\tau _Q(x)$
, and
$\langle y\xi b,\xi \rangle =\tau _Q(y)\tau _B(b)$
for every
$a\in A, ~x,y\in Q,$
and
$b\in B$
. -
(2)
$\overline {\operatorname {Span}((A\, \overline {\otimes }\, Q)\xi )}=\mathcal H=\overline {\operatorname {Span}(Q\xi B)}$
.
We prove in Proposition 3.5 that vNOE is indeed an equivalence relation. We should remark that, in the above definition,
$\mathcal H$
can also be considered as an
$A-B\, \overline {\otimes }\, Q^{\mathrm {op}}$
-bimodule satisfying conditions analogous to the two mentioned in the definition. This essentially is the reason for the symmetry of vNOE, even though the definition seems asymmetric at first. To prove transitivity, inspired by [Reference Berendschot and VaesBV25, Lemma 5.11], we establish an equivalent characterization of vNOE in Theorem 3.1, and show in Theorem 3.11 that
$\Gamma \sim _{\mathrm {vNOE}}\Lambda $
if and only if
$L\Gamma \sim _{\mathrm {vNOE}}L\Lambda $
. Since
$L(\Gamma *\Lambda )\cong L\Gamma *L\Lambda $
, Theorem 1.3 follows from the following theorem, which we prove in Section 3. We should remark that the above definition, as stated, depends on the choice of the traces
$\tau _A$
and
$\tau _B$
. Outside of the case of finite factors, it is not immediately clear whether the above definition is independent of the choice of the traces for general finite von Neumann algebras.
Theorem 1.6 If
$(A_i,\tau _{A_i}), (B_i,\tau _{B_i}), ~i=1,2$
are tracial von Neumann algebras such that
$(A_i,\tau _{A_i})\sim _{\mathrm {vNOE}}(B_i,\tau _{B_i}),~ i=1,2$
, then,
$(A_1*A_2,\tau _{A_1}*\tau _{A_2})\sim _{\mathrm {vNOE}}(B_1*B_2,\tau _{B_1}*\tau _{B_2})$
.
Similar to free products, one also has that the group von Neumann algebra of a graph product of groups is isomorphic to the (von Neumann algebraic) graph product of the group von Neumann algebras, and hence Theorem 1.4 follows from the following theorem.
Theorem 1.7 Let
$\mathcal {G}=(V,E)$
be a simple graph with at most countably infinite vertices. Let
$(A,\tau _A)$
and
$(B,\tau _B)$
be two graph products over
$\mathcal {G}$
, with tracial vertex von Neumann algebras
$\{(A_v,\tau _{A_v})\}_{v\in V}$
and
$\{(B_v,\tau _{B_v})\}_{v\in V}$
, respectively. If
$(A_v,\tau _{A_v})\sim _{\mathrm {vNOE}}(B_v,\tau _{B_v})$
for every
$v\in V$
, then
$(A,\tau _A)\sim _{\mathrm {vNOE}}(B,\tau _B)$
.
Remark 1.8 Since graph product over a totally disconnected graph, i.e., a graph with no edges, gives free product, Theorem 1.6 follows from Theorem 1.7. In particular, Theorem 1.7 shows that Theorem 1.6 holds for free products of countably many tracial von Neumann algebras similar to the result obtained by Gaboriau in [Reference GaboriauGab05, P ME 6*]. Furthermore, Horbez and Huang [Reference Horbez and HuangHH22, Proposition 4.2] proved the stability of OE under taking graph products over finite simple graphs, but our result holds for an arbitrary, countably infinite graph product. We include a proof of Theorem 1.6 for two reasons. Firstly, the notation is a little less involved compared to the proof of Theorem 1.7. Secondly, for the convenience of a reader who might be interested in the result but is not familiar with graph products.
In Proposition 3.14, we show that vNOE tracial von Neumann algebras are vNE in the sense of [Reference Ishan, Peterson and RuthIPR24]. We should remark that vNE does not imply vNOE in general.
In the final section, we obtain a partial analog of Singer’s theorem [Reference SingerSin55] for OE in the setting of vNOE of groups. As noted in [Reference Ishan, Peterson and RuthIPR24, Example 5.2], if
$\Gamma $
and
$\Lambda $
are countable discrete groups with trace-preserving actions
$\Gamma {\, \curvearrowright \,} (A,\tau _A)$
and
$\Lambda {\, \curvearrowright \,}(B,\tau _B)$
on tracial von Neumann algebras
$(A,\tau _A)$
and
$(B,\tau _B)$
, respectively, and if
$\theta :B\rtimes \Lambda \to A\rtimes \Gamma $
is a trace-preserving isomorphism such that
$\theta (B)=A$
, then
$\Gamma \sim _{\mathrm {vNOE}}\Lambda $
. As a partial converse to this, we prove the following theorem.
Theorem 1.9 If
$\Gamma $
and
$\Lambda $
are countable discrete groups such that
$\Gamma \sim _{\mathrm {vNOE}}\Lambda $
, then there exist tracial von Neumann algebras
$(A,\tau _A),~ (B,\tau _B)$
, trace-preserving actions
$\Gamma {\, \curvearrowright \,} A,~\Lambda {\, \curvearrowright \,} B$
, and a trace-preserving isomorphism
$\theta :B\rtimes \Lambda \to A\rtimes \Gamma $
.
2 Preliminaries and notations
We set up the notations and collect some facts that will be needed in this article.
2.1 Tracial von Neumann algebras and the standard form
A tracial von Neumann algebra A is endowed with a trace, i.e., a faithful, normal, unital linear functional
$\tau :A\to \mathbb {C}$
such that
$\tau (xy)=\tau (yx)$
for all
$x,y\in A$
. The trace
$\tau $
induces an inner product on A given by
$\langle x,y\rangle =\tau (y^*x), x,y\in A$
, and we let
$L^2(A)$
denote the Hilbert space completion of A with respect to this inner product. When we view an element
$x\in A$
as a vector in
$L^2(A)$
, we denote it by
$\hat x$
. An element
$x\in A$
defines a bounded linear operator on
$L^2(A)$
given by
$L_x(\hat {y})=\widehat {xy}, y\in A$
, and thus we have a representation of A in
$\mathcal {B}(L^2(A))$
, called the standard representation. There is also a canonical anti-linear conjugation operator
$J:L^2(A)\to L^2(A)$
, defined by
$J(\hat x)=\widehat {x^*}, x\in A$
, and we have that
$A'=JAJ$
, where
$A'$
is the commutant of M inside
$\mathcal {B}(L^2(A))$
. By the tracial property of
$\tau $
, for
$x\in A$
, the operator
$R_x$
on
$L^2(A)$
defined by
$R_x(\hat {y})=\widehat {yx}, y\in A$
is bounded. If we let
$\rho (A)=\{R_x:x\in A\}\subset \mathcal {B}(L^2(A))$
, then
$\rho (A)=A'$
.
2.2 Free product and amalgamated free product
Let
$(A_1,\tau _1)$
and
$(A_2,\tau _2)$
be tracial von Neumann algebras. The free product of
$A_1$
and
$A_2$
is the unique, up to isomorphism, tracial von Neumann algebra
$(A,\tau )$
containing
$A_1$
and
$A_2$
, and is such that
$\tau \vert _{A_i}=\tau _i, i=1,2$
, A is generated by
$A_1\cup A_2$
, and
$A_1,A_2$
are free inside A, i.e.,
$\tau (a_1a_2\dots a_k)=0$
, whenever
$a_i\in A_{n_i}$
with
$n_i\neq n_{i+1}$
for all
$i\in \{1,\ldots , k-1\}$
,
$n_i\in \{1,2\}$
and
$\tau _{n_i}(a_i)=0$
for all
$1\leq i\leq k$
. We will say that an element
$a_1a_2\dots a_k$
of the algebraic free product
$A_1*_{\mathrm {alg}}A_2$
is an alternating centered word with respect to
$\tau $
if
$a_i\in A_{n_i}$
with
$n_i\neq n_{i+1}$
for all
$i\in \{1,\ldots , k-1\}$
,
$n_i\in \{1,2\}$
and
$\tau _{n_i}(a_i)=0$
for all
$1\leq i\leq k$
.
For
$i=1,2$
, let
$(A_i,\tau _i)$
be tracial von Neumann algebras,
$Q\subset A_i$
be a common von Neumann subalgebra, and
$E_i:A_i\to Q$
be faithful, normal conditional expectations. The amalgamated free product
$(A, E)=(A_1, E_1)*_Q(A_2,E_2)$
is a pair of a von Neumann algebra A generated by
$A_1$
and
$A_2$
and a faithful normal conditional expectation
$E:A\to Q$
such that
$A_1$
and
$A_2$
are freely independent with respect to E:
$E(a_1a_2\dots a_k)=0$
whenever
$a_{n_i}\in A_{n_i}$
with
$n_i\in \{1,2,\}, E_{n_i}(a_i)=0$
for all
$1\leq i\leq k$
, and
$n_i\neq n_{i+1}$
for all
$i\in \{1,\ldots ,k-1\}$
. An element
$a_1a_2\dots a_k\in A$
will be called an alternating centered word with respect to E if
$a_{n_i}\in A_{n_i}$
with
$n_i\in \{1,2\}, E_{n_i}(a_i)=0$
for all
$1\leq i\leq k$
, and
$n_i\neq n_{i+1}$
for all
$i\in \{1,\ldots ,k-1\}$
.
For the construction and further details on (amalgamated) free products, we refer the reader to [Reference PopaPop93, Reference UedaUed99, Reference Voiculescu, Dykema and NicaVDN92, Reference VoiculescuVoi85].
2.3 Graph product
Let
$\mathcal {G}=(V,E)$
be a simple graph with the vertex set V and the edge set
$E\subseteq V\times V\setminus \{(v,v) : v\in V\}$
. We assume that the graph
$\mathcal {G}$
is non-oriented, i.e.,
$(v,w)\in E$
if and only if
$(w,v)\in E$
. A word
$v_1v_2\dots v_n$
of vertices in V is called reduced if it satisfies the following property: if there exist
$k<l$
such that
$v_k=v_l$
, then there is some
$k<j<l$
such that
$(v_k,v_j)\notin E$
. Let
$\mathcal {G}=(V,E)$
be a simple graph,
$(A,\tau )$
be a tracial von Neumann algebra, and
$\{(A_v,\tau _v) : v\in V\}$
be a family of tracial von Neumann subalgebras of
$(A,\tau )$
such that
$\tau \vert _{A_v}=\tau _v$
for all
$v\in V$
. We say that the family
$\{(A_v,\tau _v) : v\in V\}$
is
$\mathcal {G}$
-independent if the following property holds: if
$v_1\dots v_n$
is a reduced word and
$a_1,\ldots , a_n\in A$
are such that
$a_i\in A_{v_i}$
and
$\tau (a_i)=0$
, then
$\tau (a_1\dots a_n)=0$
. On the other hand, given a simple graph
$\mathcal {G}=(V,E)$
and a family of tracial von Neumann algebras
$\{(A_v,\tau _v) : v\in V\}$
, there is a unique, up to isomorphism, tracial von Neumann algebra
$(A,\tau )$
, called the graph product over
$\mathcal {G}$
of the family
$\{(A_v,\tau _v) : v\in V\}$
, and trace-preserving inclusions
$\varphi _v: A_v\hookrightarrow A$
such that the family
$\{\varphi _v(A_v):v\in V\}$
is
$\mathcal {G}$
-independent and generates A as a von Neumann algebra (see [Reference MłotkowskiMło04, Reference Caspers and FimaCF17]). We denote the graph product
$(A,\tau )$
of the family
$\{(A_v,\tau _v) : v\in V\}$
by
$$ \begin{align*} (A,\tau)=\bigstar_{v\in V}(A_v,\tau_v). \end{align*} $$
Remark 2.1 If
$\mathcal {G}=(V,E)$
is a simple graph, and
$\{\Gamma _v : v\in V\}$
is a family of countable discrete groups, then
$L(\bigstar _{v\in V}\Gamma _v)=\bigstar _{v\in V}L\Gamma _v$
(see [Reference Caspers and FimaCF17, Remark 3.23]).
2.4 Modules over tracial von Neumann algebras
For details on the proofs of the facts collected in this section, we refer the reader to [Reference Anantharaman and PopaAP21, Chapter 8].
Definition 2.2 Given von Neumann algebras A and B,
-
(1) a left A-module is a pair
$(\mathcal H,\pi _A)$
, where
$\mathcal H$
is a Hilbert space and
$\pi _A:A\to \mathcal {B}(\mathcal H)$
is a normal unital
$*$
-homomorphism. -
(2) a right B-module is a pair
$(\mathcal H,\pi _B)$
, where
$\mathcal H$
is a Hilbert space and
$\pi _B:B\to \mathcal {B}(\mathcal H)$
is a normal unital
$*$
-anti-homomorphism, i.e.,
$\pi _B(xy)=\pi _B(y)\pi _B(x)$
for all
$x,y\in B$
. In other words,
$\mathcal H$
is a left
$B^{\mathrm {op}}$
-module, where
$B^{\mathrm {op}}$
is the opposite algebra. -
(3) an
$A-B$
-bimodule is a triple
$(\mathcal H,\pi _A,\pi _B)$
such that
$(\mathcal H,\pi _A)$
is a left A-module,
$(\mathcal H,\pi _B)$
is a right B-module, and the representations
$\pi _A$
and
$\pi _B$
commute. For
$\xi \in \mathcal H$
,
$x\in A$
, and
$y\in B$
, we will write
$x\xi y$
instead of
$\pi _A(x)\pi _B(y)\xi ~(=\pi _B(y)\pi _A(x)\xi ).$
Definition 2.3 Let
$(A,\tau _A), (B,\tau _B)$
be tracial von Neumann algebras and let
$\mathcal H$
be an
$A-B$
-bimodule. A vector
$\xi \in \mathcal H$
is called:
-
(1) tracial if
$\langle x\xi ,\xi \rangle =\tau _A(x)$
for every
$x\in A$
, and
$\langle \xi y,\xi \rangle =\tau _B(y)$
for every
$y\in B$
; -
(2) bi-tracial if
$\langle x\xi y,\xi \rangle =\tau _A(x)\tau _B(y)$
for all
$x\in A, y\in B$
; -
(3) cyclic if
$\overline {\mathrm {Span}\{x\xi y:x\in A, y\in B\}}=\mathcal H$
.
Let
$(Q,\tau _Q)$
be a tracial von Neumann algebra. Given two left Q-modules
$\mathcal H$
and
$\mathcal K$
, we denote by
$_Q\mathcal {B}(\mathcal H,\mathcal K)$
the space of left Q-linear bounded maps from
$\mathcal H$
into
$\mathcal K$
, that is,
$$ \begin{align*} _Q\mathcal{B}(\mathcal H,\mathcal K)=\{T\in\mathcal{B}(\mathcal H,\mathcal K): T(x\xi)=x(T\xi) \text{ for all } x\in Q, \xi\in \mathcal H\}. \end{align*} $$
We set
$_Q\mathcal {B}(\mathcal H)={_Q\mathcal {B}(\mathcal H,\mathcal H)}$
. It is straightforward to check that
$_Q\mathcal {B}(\mathcal H)=Q'\cap \mathcal {B}(\mathcal H)$
. Moreover,
$_Q\mathcal {B}(\mathcal H)$
is a semi-finite von Neumann algebra equipped with a specific semi-finite trace
$\mathrm {Tr}$
, depending on
$\tau _Q$
. Before stating the result that characterizes
$\mathrm {Tr}$
, observe that, given
$S,T\in {_Q\mathcal {B}(L^2Q,\mathcal H)}$
, we have
$TS^*\in {_Q\mathcal {B}(\mathcal H)}$
, and
$S^*T\in JQJ$
, where
$J:L^2Q\to L^2Q$
is the canonical conjugation operator. The following is a translation of [Reference Anantharaman and PopaAP21, Proposition 8.4.2] for left Q-modules.
Proposition 2.4 If
$\mathcal H$
is a left Q-module over a tracial von Neumann algebra
$(Q,\tau _Q)$
, then the commutant
$_Q\mathcal {B}(\mathcal H)=Q'\cap \mathcal {B}(\mathcal H)$
is a semi-finite von Neumann algebra equipped with a canonical faithful normal semi-finite trace
$\mathrm {Tr}$
characterized by the equation
$$ \begin{align*} \mathrm{Tr}(TT^*)=\tau_Q(JT^*TJ) \end{align*} $$
for every left Q-linear bounded operator
$T:L^2Q\to \mathcal H$
.
Remark 2.5 Suppose
$(Q,\tau _Q)$
is a tracial von Neumann algebra and
$\mathcal H$
is a left Q-module. If
$\xi \in \mathcal H$
is a tracial vector, then the orthogonal projection
$P:\mathcal H\to \overline {\operatorname {Span}(Q\xi )}$
lies in
$_Q\mathcal {B}(\mathcal H)$
. Moreover, since
$\xi $
is tracial, the operator
$U:L^2Q\to \overline {\operatorname {Span}(Q\xi )}$
given by
$U\hat {x}=x\xi , x\in Q$
is a unitary. Extending U to an isometry from
$L^2Q$
into
$\mathcal H$
in an obvious way and applying Proposition 2.4 to
$T=PU:L^2Q\to \mathcal H$
yields that
$\mathrm {Tr}(P)=\tau _Q(1)=1$
.
2.5 Actions on semi-finite von Neumann algebras
For a semi-finite von Neumann algebra
$\mathcal {M}$
with a faithful normal semi-finite trace
$\mathrm {Tr}$
, the set
$\mathfrak n_{\mathrm {Tr}} = \{ x \in \mathcal M \mid \mathrm {Tr}(x^*x) < \infty \}$
is an ideal. Left multiplication of
$\mathcal M$
on
$\mathfrak n_{\mathrm {Tr}}$
induces a normal faithful representation of
$\mathcal M$
in
$\mathcal B(L^2(\mathcal M, \mathrm {Tr}))$
, called the standard representation, where
$L^2(\mathcal {M},\mathrm {Tr})$
is the Hilbert space completion of
$\mathfrak n_{\mathrm {Tr}}$
under the inner product
$\langle a, b \rangle _2 = \mathrm {Tr}(b^* a)$
.
If
$\Gamma {\, \curvearrowright ^{\sigma } \,} \mathcal M$
is a trace-preserving action of a countable discrete group
$\Gamma $
on
$\mathcal {M}$
, then
$\Gamma $
preserves the
$\| \cdot \|_2$
-norm on
$\mathfrak n_{\mathrm {Tr}}$
. Therefore, restricted to
$\mathfrak n_{\mathrm {Tr}}$
, the action is isometric with respect to the
$\| \cdot \|_2$
-norm and hence gives a unitary representation
$\sigma ^0:\Gamma \to \mathcal U(L^2(\mathcal M, \mathrm {Tr}))$
, called the Koopman representation. Considering
$\mathcal M \subset \mathcal B(L^2(\mathcal M, \mathrm {Tr}))$
via the standard representation, we have that the action
$\sigma : \Gamma \to \mathrm {Aut}(\mathcal M, \mathrm { Tr})$
is unitarily implemented via the Koopman representation, i.e., for
$x \in \mathcal M$
and
$\gamma \in \Gamma ,$
we have
$\sigma _\gamma (x) = \sigma _\gamma ^0 x \sigma _{\gamma ^{-1}}^0$
(see [Reference HaagerupHaa75, Theorem 3.2]).
3 Von Neumann orbit equivalence
In this section, we define vNOE for tracial von Neumann algebras and for countable discrete groups. We shall see that groups are vNOE if and only if the corresponding group von Neumann algebras are, and we conclude this section with the proof that vNOE tracial von Neumann algebras are vNE in the sense of [Reference Ishan, Peterson and RuthIPR24].
3.1 Von Neumann orbit equivalence for tracial von Neumann algebras
Theorem 3.1 Let
$(A,\tau _A)\text { and } (B,\tau _B)$
be tracial von Neumann algebras. Then, the following are equivalent:
-
(1) There exists a tracial von Neumann algebra
$(Q,\tau _Q)$
and a pointed
$A\, \overline {\otimes }\, Q-B$
-bimodule
$(\mathcal H,\xi )$
such that
$\xi \in \mathcal H$
is a cyclic and (bi-)tracial vector for both
$A\, \overline {\otimes }\, Q$
-module structure, and
$Q-B$
-bimodule structure. That is, for all
$a\in A, b\in B$
, and
$x\in Q$
,-
(a)
$\langle (a\otimes x)\xi ,\xi \rangle =\tau _A(a)\tau _Q(x)$
, and
$\langle x\xi b, \xi \rangle =\tau _Q(x)\tau _B(b)$
; -
(b)
$\overline {\mathrm {Span}((A\, \overline {\otimes }\, Q)\xi )}=\mathcal H=\overline {\mathrm {Span}(Q\xi B)}$
.
-
-
(2) There exists a tracial von Neumann algebra
$(Q,\tau _Q)$
, and a normal
$*$
-homomorphism
$\phi :B\to A\, \overline {\otimes }\, Q$
such that:-
(a)
$\mathbb E_Q\circ \phi =\tau _B$
, where
$\mathbb E_Q:A\, \overline {\otimes }\, Q\to Q$
is the normal conditional expectation; -
(b)
$\overline {\mathrm {Span}\{x\phi (b):b\in B, x\in Q\}}^{\|\cdot \|_2}=L^2(A\, \overline {\otimes }\, Q)$
.
-
Proof Let
$(\mathcal H,Q,\xi )$
be a triple as in (1). We thus obtain a canonical unitary
$U\colon \mathcal H\to L^{2}(A\overline {\otimes }Q)$
such that
$U(y\xi )=\hat y$
for all
$y\in A\overline {\otimes }Q$
. Hence, we can define a right action of B on
$L^{2}(A\overline {\otimes }Q)$
by
$$\begin{align*}\eta\cdot b=U(U^{*}(\eta)b), \text{ for all } \eta\in L^{2}(A\overline{\otimes}Q), b\in B.\end{align*}$$
For
$b\in B$
, we let
$R_{b}\in \mathcal {B}(L^{2}(A\overline {\otimes }Q))$
be the operator corresponding to right multiplication by b. Since
$\mathcal H$
is an
$A\overline {\otimes }Q-B$
bimodule, and U is
$A\, \overline {\otimes }\, Q$
-linear, so, the right action of B commutes with the left action of
$A\overline {\otimes }Q$
on
$L^2(A\, \overline {\otimes }\, Q)$
, and hence
$R_b\in (A\, \overline {\otimes }\, Q)'\cap \mathcal {B}(L^2(A\, \overline {\otimes }\, Q))$
for every
$b\in B$
. Since the commutant of
$A\overline {\otimes }Q$
acting on
$L^{2}(A\overline {\otimes }Q)$
is
$\rho (A\overline {\otimes }Q)$
we define
$\phi \colon B\to A\overline {\otimes }Q$
as follows: for
$b\in B$
,
$\phi (b)$
is the unique element in
$A\, \overline {\otimes }\, Q$
such that
$R_{b}=\rho (\phi (b))$
. This is directly checked to be a normal
$*$
-homomorphism. Moreover, by definition of
$\phi $
, we have that
$\eta \cdot b=\eta \phi (b),$
for every
$\eta \in L^2(A\, \overline {\otimes }\, Q), b\in B$
. Since
$\xi $
is Q-B bi-tracial, we have for all
$b\in B,x\in Q$
that
$$\begin{align*}\tau_{Q}(x)\tau_{B}(b)=\langle x\xi b,\xi\rangle=\langle U^*(\hat x)b,U^*(\hat 1)\rangle=\langle \widehat{x\phi(b)},\hat 1\rangle=\tau(x\phi(b)),\end{align*}$$
where
$\tau $
denotes the trace on
$A\, \overline {\otimes }\, Q$
. Furthermore, since
$\tau _Q\circ \mathbb E_Q=\tau $
, we have
$$ \begin{align*} \tau_Q(\tau_B(b)x)=\tau(x\phi(b))=\tau_Q(\mathbb E_Q(x\phi(b)))=\tau_Q(x\mathbb E_Q(\phi(b))), \end{align*} $$
for all
$x\in Q, b\in B$
, whence it follows that
$\mathbb E_{Q}\circ \phi =\tau _{B}$
. Finally,
$$\begin{align*}\overline{\mathrm{Span}\{x\phi(b):x\in Q,b\in B\}}^{\|\cdot\|_{2}}=U(\overline{\mathrm{Span}\{x\xi b:x\in Q,b\in B\}})=U(\mathcal H)=L^{2}(A\overline{\otimes}Q).\end{align*}$$
Conversely, suppose condition (2) holds, and let
$\mathcal H=L^{2}(A\overline {\otimes }Q)$
, and
$\xi =\hat 1$
. Define a right action of B on
$\mathcal H$
by
$\eta \cdot b=\eta \phi (b)$
. Then, for
$x\in Q$
,
$b\in B,$
we have
$$\begin{align*}\overline{\mathrm{Span}\{x\xi\cdot b:x\in Q,b\in B\}}^{\|\cdot\|_{2}}=\overline{\mathrm{Span}\{x\phi(b):x\in Q,b\in B\}}^{\|\cdot\|_{2}}=L^{2}(A\overline{\otimes}Q),\end{align*}$$
and for
$x\in Q,b\in B,$
we have
$$\begin{align*}\langle x\xi\cdot b,\xi\rangle=\langle \widehat{x\phi(b)},\hat 1\rangle=\tau(x\phi(b))=\tau_Q(x\mathbb E_{Q}(\phi(b)))=\tau_Q(x)\tau_{B}(b).\end{align*}$$
Remark 3.2 Since the operation of taking adjoints is isometric on
$L^2(A\, \overline {\otimes }\, Q)$
, in condition (2) of Theorem 3.1, one might equivalently require that
$\overline {\operatorname {Span}\{\phi (b)x:b\in B,x\in Q\}}^{\|\cdot \|_{2}}=L^{2}(A\overline {\otimes }Q)$
.
Definition 3.3 Let
$(A,\tau _A)$
and
$(B,\tau _B)$
be tracial von Neumann algebras. We say that
$(A,\tau _A)$
is vNOE to
$(B,\tau _B)$
, denoted
$(A,\tau _A)\sim _{\mathrm {vNOE}}(B,\tau _B)$
, if either of the two equivalent conditions in Theorem 3.1 is satisfied. If
$(A,\tau _A)$
is vNOE to
$(B,\tau _B)$
, then the triple
$(\mathcal H,Q,\xi )$
or the pair
$(Q,\phi )$
of Theorem 3.1 will be called a vNOE-coupling between
$(A,\tau _A)$
and
$(B,\tau _B)$
.
Remark 3.4 As mentioned in the introduction, the above definition depends on the choice of the traces
$\tau _A$
and
$\tau _B$
. When in a situation where the traces are fixed, and there is no risk of confusion, we will often drop them, and simply say that A and B are vNOE and write
$A\sim _{\mathrm {vNOE}}B$
.
Proposition 3.5 vNOE is an equivalence relation.
Proof If
$(A,\tau _A)$
is a tracial von Neumann algebra, then taking
$Q=\mathbb C, \mathcal H=L^2(A)$
, and
$\xi =\hat 1\in L^2(A)$
in condition (1) of Theorem 3.1 shows that
$A\sim _{\mathrm {vNOE}}A$
. To see symmetry, let
$(A,\tau _A)$
and
$(B,\tau _B)$
be tracial von Neumann algebras satisfying condition (1) of Theorem 3.1, and let
$\mathcal H, (Q,\tau _Q), \text { and } \xi \in \mathcal H$
be as in the condition. Note that we can view
$\mathcal H$
as an
$A-B\, \overline {\otimes }\, Q^{\mathrm {op}}$
-bimodule. Consider the conjugate Hilbert space
$\overline {\mathcal H}$
, and the corresponding canonical
$B\, \overline {\otimes }\, Q^{\mathrm {op}}-A$
bimodule structure on
$\overline {\mathcal H}$
. Then, it is straightforward to check that the triple
$(\overline {\mathcal H},Q^{\mathrm {op}},\bar {\xi })$
satisfies (1) of Theorem 3.1 and thus,
$B\sim _{\mathrm {vNOE}}A$
. To show transitivity, we will use condition (2) of Theorem 3.1. To this end, let
$(A,\tau _A), (B,\tau _B)$
, and
$(C,\tau _C)$
be tracial von Neumann algebras. Let
$Q_1, Q_2$
, and
$\phi _1:B\to A\, \overline {\otimes }\, Q_1, \phi _2:C\to B\, \overline {\otimes }\, Q_2$
be as in (2) of Theorem 3.1. Let
$Q=Q_1\, \overline {\otimes }\, Q_2$
and let
$\phi :C\to A\, \overline {\otimes }\, Q$
be given by
$$ \begin{align*} \phi(c)=(\phi_1\otimes\mathrm{id}_{Q_2})(\phi_2(c)), ~~~ c\in C, \end{align*} $$
where
$\phi _1\otimes \mathrm {id}_{Q_2}:B\, \overline {\otimes }\, Q_2\to A\, \overline {\otimes }\, Q_1\, \overline {\otimes }\, Q_2$
is the natural extension of
$\phi _1:B\to A\, \overline {\otimes }\, Q_1$
. Let
$\mathbb E_{Q_1}:A\, \overline {\otimes }\, Q_1\to Q_1, \mathbb E_{Q_2}:B\, \overline {\otimes }\, Q_2\to Q_2, \text {and }\mathbb E_Q:A\, \overline {\otimes }\, Q_1\, \overline {\otimes }\, Q_2\to Q_1\, \overline {\otimes }\, Q_2$
be normal conditional expectations. Consider the map
$\mathbb E_{Q_1}\otimes \mathrm {id}_{Q_2}:A\, \overline {\otimes }\, Q_1\, \overline {\otimes }\, Q_2\to Q_1\, \overline {\otimes }\, Q_2$
. Note that
$\mathbb E_Q=\mathbb E_{Q_1}\otimes \mathrm {\operatorname {id}}_{Q_2}$
. Therefore,
$$ \begin{align*} \mathbb E_Q\circ\phi=(\mathbb E_{Q_1}\otimes \operatorname{id}_{Q_2})\circ ((\phi_1\otimes\mathrm{id}_{Q_2})\circ\phi_2)=\mathbb E_{Q_2}\circ \phi_2=\tau_C, \end{align*} $$
where the second to last equality follows from the fact that the following diagram, since
${\mathbb E}_{Q_1}\circ \phi _1=\tau _B$
, is commutative:
Now, consider
$V=\overline {\operatorname {Span}\{\phi (c)x : x\in Q, c\in C\}}^{\|\cdot \|_2},$
and note that V is invariant under multiplication on the right by elements of
$Q=Q_1\, \overline {\otimes }\, Q_2$
. In the light of Remark 3.2, it suffices to show that
$V=L^2(A\, \overline {\otimes }\, Q)$
, and for this, since V is invariant under right multiplication by Q, it suffices to show that
$A\otimes 1\otimes 1\subseteq V$
. Recall that
$$ \begin{align*}\overline{\operatorname{Span}\{\phi_2(c)x_2 : c\in C, x_2\in Q_2\}}^{\|\cdot\|_2}=L^2(B\, \overline{\otimes}\, Q_2)\supseteq B\, \overline{\otimes}\, Q_2.\end{align*} $$
Hence, we have
$$ \begin{align*}\overline{\operatorname{Span}\{(\phi_1\otimes\operatorname{id}_{Q_2})(\phi_2(c)(1\otimes x_2)) : c\in C, x_2\in Q_2\}}^{\|\cdot\|_2}\supseteq (\phi_1\otimes\operatorname{id}_{Q_2})(B\, \overline{\otimes}\, Q_2).\end{align*} $$
Moreover, since
$\phi _1$
is unital and
$\phi _1\otimes \operatorname {id}_{Q_2}$
is a homomorphism, we also have that
$$ \begin{align*}(\phi_1\otimes\operatorname{id}_{Q_2})(\phi_2(c)(1\otimes x_2))=(\phi_1\otimes\operatorname{id}_{Q_2})(\phi_2(c))(1\otimes x_2) \quad \text{ for all } c\in C, x_2\in Q_2. \end{align*} $$
Finally, since
$\overline {\operatorname {Span}\{\phi _1(b)x_1 : b\in B, x_1\in Q_1\}}^{\|\cdot \|_2}=L^2(A\, \overline {\otimes }\, Q_1)\supseteq A\, \overline {\otimes }\, Q_1$
, the following computation completes the proof:
$$ \begin{align*} V&\supseteq \overline{\operatorname{Span}\{(\phi_1\otimes\operatorname{id}_{Q_2})(\phi_2(c))(x_1\otimes x_2) : c\in C, x_1\in Q_1, x_2\in Q_2\}}^{\|\cdot\|_2}\\ &\supseteq \overline{\operatorname{Span}\{(\phi_1\otimes\operatorname{id}_{Q_2})((\phi_2(c)(1\otimes x_2))(x_1\otimes 1) : c\in C, x_1\in Q_1, x_2\in Q_2\}}^{\|\cdot\|_2}\\ &\supseteq \overline{\operatorname{Span}\{(\phi_1\otimes\operatorname{id}_{Q_2})(b\otimes 1)(x_1\otimes 1): b\in B, x_1\in Q_1\}}^{\|\cdot\|_2}\\ &\supseteq A\otimes 1\otimes 1.\\[-35pt] \end{align*} $$
Checking
$\overline {\operatorname {Span}\{\phi (b)x:b\in B,x\in Q\}}^{\|\cdot \|_2}=L^{2}(A\overline {\otimes }Q)$
might not be easy in general. However, the following lemma simplifies verifying it in certain examples.
Lemma 3.6 Let
$(A,\tau _{A}),(B,\tau _{B}),$
and
$(Q,\tau _{Q})$
be tracial von Neumman algebras. Let
$\phi \colon B\to A\overline {\otimes }Q$
be a
$*$
-homomorphism satisfying
${\mathbb E}_{Q}\circ \phi =\tau _{B}$
, where
$\mathbb E_Q:A\, \overline {\otimes }\, Q\to Q$
is the normal conditional expectation. Let
$V=\overline {\operatorname {Span}\{\phi (b)x:b\in B,x\in Q\}}^{\|\cdot \|_{2}}\subset L^{2}(A\overline {\otimes }Q)$
. Then,
$N=\{a\in A:a\otimes 1\in V\}$
is an SOT-closed subalgebra of A.
Proof The fact that N is SOT-closed follows from the fact that SOT-convergence in A implies
$\|\cdot \|_{2}$
-convergence. First note that V is invariant under left multiplication by elements of
$\phi (B)$
and right multiplication by elements of Q. We prove the following claim, whence the lemma follows immediately.
Claim For
$\eta \in V$
and
$a\in N,$
we have that
$\eta (a\otimes 1)\in V$
.
Proof of Claim
Given
$\eta \in V$
and
$a\in N$
, let
$\{x_{n}\}_{n\in \mathbb {N}}\subset \mathrm {Span}\{\phi (b)x:b\in B,x\in Q\}$
be such that
$\|x_{n}-\eta \|_{2}\to 0$
. Since
$a\otimes 1$
is bounded, it follows that
$$ \begin{align*}\|x_{n}(a\otimes 1)-\eta(a\otimes 1)\|_{2}\leq \|x_{n}-\eta\|_{2} \|a\|\to 0, \end{align*} $$
as
$n\to \infty $
. Since V is
$\|\cdot \|_{2}$
-closed, it suffices to show that
$x_{n}(a\otimes 1)\in V$
for all
$n\in \mathbb {N}$
. To this end, fix
$n\in \mathbb {N}$
, and write
$x_{n}=\sum _{j=1}^{k}\phi (b_{j})y_{j}$
with
$b_{j}\in B,y_{j}\in Q$
. Then,
$$\begin{align*}x_{n}(a\otimes 1)=\sum_{j=1}^{k}\phi(b_{j})y_{j}(a\otimes 1)=\sum_{j=1}^{k}\phi(b_{j})(a\otimes 1)y_{j},\end{align*}$$
where, in the last equality, we use that
$A \text { and } Q$
commute in
$A\overline {\otimes }Q$
. Since we already noted that V is invariant under left multiplication by
$\phi (B)$
and right multiplication by Q, and
$a\otimes 1\in V$
, it follows that
$x_{n}(a\otimes 1)\in V$
.
Remark 3.7 We do not know if N is a
$*$
-subalgebra.
Theorem 3.8 If
$(A_i,\tau _{A_i}), (B_i,\tau _{B_i}), ~i=1,2$
are tracial von Neumann algebras such that
$(A_i,\tau _{A_i})\sim _{\mathrm {vNOE}}(B_i,\tau _{B_i}),~ i=1,2$
, then,
$(A_1*A_2,\tau _{A_1}*\tau _{A_2})\sim _{\mathrm {vNOE}}(B_1*B_2,\tau _{B_1}*\tau _{B_2})$
.
Proof Since vNOE is an equivalence relation, it suffices to show that if
$A\sim _{\mathrm {vNOE}}B$
and if
$(C,\tau _C)$
is another tracial von Neumann algebra, then
$A*C\sim _{\mathrm {vNOE}}B*C$
. Let
$(Q,\tau _Q)$
be a tracial von Neumann algebra and
$\phi \colon B\to A\overline {\otimes }Q$
be a
$*$
-homomorphism as in condition (2) of Theorem 3.1. For tracial von Neumann algebra
$(C,\tau _{C})$
, we view
$(A*C)\overline {\otimes }Q$
as
$(A\overline {\otimes }Q)*_{Q}(C\overline {\otimes }Q)$
. Define
$\widetilde {\phi }_{0}\colon B*_{\text {alg}}C\to (A\overline {\otimes }Q)*_{Q}(C\overline {\otimes }Q)$
by declaring that
$\widetilde {\phi }_{0}(b)=\phi (b)*_{Q}1$
for
$b\in B$
and
$\widetilde {\phi }_{0}(c)=1*_Qc$
for
$c\in C$
. Let
${\mathbb E}_Q:(A*C)\, \overline {\otimes }\, Q\to Q$
be the normal conditional expectation. Note that
${\mathbb E}_{Q}\circ \phi =\tau _{B}$
and
${\mathbb E}_{Q}|_{C\, \overline {\otimes }\, Q}=\tau _{C}\otimes \operatorname {id}_Q$
. Therefore, if
$x\in B*_{\text {alg}}C$
is an alternating centered word with respect to
$\tau _{B*C}$
, then
$\widetilde {\phi }_{0}(x)$
is an alternating centered word with respect to
${\mathbb E}_{Q}$
. Hence,
${\mathbb E}_{Q}\circ \widetilde {\phi }_{0}=\tau _{B*C}$
. Since
${\mathbb E}_Q$
is trace-preserving, it follows that
$\widetilde {\phi }_{0}$
is trace-preserving, and thus extends to a unique trace-preserving
$*$
-homomorphism
$\widetilde {\phi }\colon B*C\to (A\overline {\otimes }Q)*_{Q}(C\overline {\otimes }Q)$
. Moreover, by continuity, we still have
${\mathbb E}_{Q}\circ \widetilde {\phi }=\tau _{B*C}$
. In light of Remark 3.2, it thus remains to check that
$\overline {\operatorname {Span}\{\widetilde {\phi }(x)y : x\in B*C, y\in Q\}}^{\|\cdot \|_2}=L^2((A*C)\, \overline {\otimes }\, Q)$
. To this end, set
$V=\overline {\operatorname {Span}\{\widetilde {\phi }(x)y:x\in B*C,y\in Q\}}^{\|\cdot \|_{2}}$
. Since V is invariant under right multiplication by Q, to show that
$V=L^{2}((A*C)\, \overline {\otimes }\, Q)$
, it suffices to show that
$ (A*C)\otimes 1\subseteq V$
. For this, by Lemma 3.6, it suffices to show that V contains
$A\otimes 1$
and
$C\otimes 1$
. That
$C\otimes 1\subseteq V$
follows from the fact that
$\widetilde {\phi }$
takes the copy of C in
$B*C$
to the copy of C in
$(A*C)\overline {\otimes }Q$
, and since
$\overline {\operatorname {Span}\{\phi (b)y:b\in B,y\in Q\}}^{\|\cdot \|_2}=L^{2}(A\overline {\otimes }Q)$
, we also have that
$A\otimes 1\subseteq V$
.
We conclude this section by proving Theorem 1.7, which we recall below.
Theorem 3.9 Let
$\mathcal {G}=(V,E)$
be a simple graph, with at most countably infinite vertices. Let
$(A,\tau _A)$
and
$(B,\tau _B)$
be two graph products over
$\mathcal {G}$
, with tracial vertex von Neumann algebras
$\{(A_v,\tau _{A_v})\}_{v\in V}$
and
$\{(B_v,\tau _{B_v})\}_{v\in V}$
, respectively. If
$(A_v,\tau _{A_v})\sim _{\mathrm {vNOE}}(B_v,\tau _{B_v})$
for every
$v\in V$
, then
$(A,\tau _A)\sim _{\mathrm {vNOE}}(B,\tau _B)$
.
Proof Let
$(Q_v,\phi _v)$
be a vNOE-coupling between
$(A_v,\tau _{A_v})$
and
$(B_v,\tau _{B_v})$
, where
$\phi _v:A_v\to B_v\, \overline {\otimes }\, Q_v$
is a normal unital
$*$
-homomorphism satisfying
$$ \begin{align*} {\mathbb E}_v\circ\phi_v=\tau_{A_v} \qquad \text{ and } \qquad \overline{\operatorname{Span}\{\phi_v(a)x: a\in A_v, x\in Q_v\}}^{\|\cdot\|_2}=L^2(B_v\, \overline{\otimes}\, Q_v), \end{align*} $$
here,
${\mathbb E}_v:B_v\, \overline {\otimes }\, Q_v\to Q_v$
is the normal conditional expectation. Define
$(Q,\tau _Q)$
to be the tensor product
$\, \overline {\otimes }\,_{v\in V}(Q_v,\tau _{Q_v})$
. We now define a
$*$
-homomorphism
$\phi :A\to B\, \overline {\otimes }\, Q$
and show that it has the desired properties. To this end, first note that if v and w are two distinct vertices connected by an edge, then
$B_v$
commutes with
$B_w$
and
$Q_v$
commutes with
$Q_w$
as
$v\neq w$
. Thus,
$\phi _v(A_v)$
and
$\phi _w(A_w)$
commute inside
$B\, \overline {\otimes }\, Q$
, and therefore, we can define
$\phi $
on the algebraic graph product (i.e., the universal unital
$*$
-algebra generated by the
$\{A_v\}_{v\in V}$
subject to the relation that
$A_v$
commutes with
$A_w$
whenever v and w are connected by an edge). In particular, note that
$\phi (a)=\phi _v(a)$
, whenever
$a\in A_v$
. Next, we show that
$\phi $
extends to a normal unital
$*$
-homomorphism on A and satisfies
${\mathbb E}_Q(\phi (a))=\tau _A(a)$
for all
$a\in A$
, where
${\mathbb E}_Q:B\, \overline {\otimes }\, Q\to Q$
is the normal conditional expectation. To see this, we note that for any reduced word
$v=v_1\dots v_n$
of vertices, and elements
$a_i\in A_{v_i}$
of trace zero,
$1\leq i\leq n$
, we have that
$$ \begin{align*} {\mathbb E}_Q(\phi_{v_1}(a_1)\dots\phi_{v_n}(a_n))=0. \end{align*} $$
Indeed, for every
$i\in \{1,\ldots ,n\}$
, we have
${\mathbb E}_{v_i}(\phi _{v_i}(a_i))=\tau _{A_{v_i}}(a_i)=0,$
so,
$\phi _{v_i}(a_i)$
can be approximated by linear combinations of elements of the form
$b_{v_i}\otimes q_{v_i}$
, where
$b_{v_i}\in B_{v_i}, q_{v_i}\in Q_{v_i}$
with
$\tau _{B_{v_i}}(b_{v_i})=0$
. Thus,
${\mathbb E}_Q(\phi _{v_1}(a_1)\dots \phi _{v_n}(a_n))=0$
and hence it follows that the map
$\phi $
, defined on the algebraic graph product, is trace-preserving. Therefore, by [Reference Caspers and FimaCF17, Proposition 3.22],
$\phi $
extends to a well-defined normal unital
$*$
-homomorphism on A. Furthermore, if either
$a=1$
or
$a\in A$
is any reduced operator (see [Reference Caspers and FimaCF17, Definition 3.10]), then we have seen that
${\mathbb E}_Q(\phi (a))=0=\tau _A(a)$
. Since the linear span of
$1$
and reduced operators is a dense
$*$
-subalgebra of A, we conclude that
${\mathbb E}_Q(\phi (a))=\tau _A(a)$
for all
$a\in A$
. Finally, to show that
$\overline {\operatorname {Span}\{\phi (a)x:a\in A, x\in Q\}}^{\|\cdot \|_2}=L^2(B\, \overline {\otimes }\, Q)$
, it suffices to show that
$$ \begin{align} \overline{\operatorname{Span}(\phi_{v_1}(A_{v_1})\dots\phi_n(A_{v_n})(1\otimes Q))}^{\|\cdot\|_2}=\overline{\operatorname{Span}(B_{v_1}\dots B_{v_n}(1\otimes Q))}^{\|\cdot\|_2}, \end{align} $$
for any reduced word
$v=v_1\dots v_n$
of vertices and for all n. We proceed by induction. It is straightforward to see that for any vertex v,
$\overline {\operatorname {Span}(\phi _v(A_v)(1\otimes Q))}^{\|\cdot \|_2}=L^2(B_v\, \overline {\otimes }\, Q)=\overline {\operatorname {Span}(B_v(1\otimes Q))}^{\|\cdot \|_2}$
. Suppose that (*) holds for any reduced word
$v_1\dots v_n$
of length n and let
$v_1\dots v_nv_{n+1}$
be any reduced word of length
$n+1$
. Then,
$$ \begin{align*} &\overline{\operatorname{Span}(\phi_{v_1}(A_{v_1})\dots\phi_{v_{n+1}}(A_{n+1})(1\otimes Q))}^{\|\cdot\|_2}\\&\quad=\overline{\operatorname{Span}(\phi_{v_1}(A_{v_1})B_{v_2}\dots B_{v_{n+1}}(1\otimes Q))}^{\|\cdot\|_2}\\ &\quad=\overline{\operatorname{Span}(\phi_{v_1}(A_{v_1})(1\otimes Q)(B_{v_2}\dots B_{v_{n+1}}\otimes 1))}^{\|\cdot\|_2}\\ &\quad=\overline{\operatorname{Span}(B_{v_1}(1\otimes Q)(B_{v_2}\dots B_{v_{n+1}}\otimes 1))}^{\|\cdot\|_2}\\ &\quad=\overline{\operatorname{Span}(B_{v_1}B_{v_2}\dots B_{v_{n+1}}(1\otimes Q))}^{\|\cdot\|_2}. \end{align*} $$
Thus,
$(A,\tau _A)\sim _{\mathrm {vNOE}}(B,\tau _B)$
.
3.2 Von Neumann orbit equivalence for groups
Let
$\Gamma {\, \curvearrowright \,}^\sigma \mathcal {M}$
be an action of a countable discrete group
$\Gamma $
on a von Neumann algebra
$\mathcal {M}$
. A fundamental domain for the action is a projection
$p\in \mathcal {M}$
such that the projections
$\{\sigma _\gamma (p)\}_{\gamma \in \Gamma }$
are pairwise orthogonal and
$\sum _{\gamma \in \Gamma }\sigma _\gamma (p)=1$
, where the sum converges in the strong operator topology. Two countable discrete groups
$\Gamma $
and
$\Lambda $
are said to be vNE, denoted
$\Gamma \sim _{\mathrm {vNE}}\Lambda $
, if there exists a semi-finite von Neumann algebra
$(\mathcal {M},\mathrm {Tr})$
with a faithful normal semi-finite trace
$\mathrm {Tr}$
, and commuting trace-preserving actions
$\Gamma {\, \curvearrowright \,}^\sigma \mathcal {M}$
and
$\Lambda {\, \curvearrowright \,}^\alpha \mathcal {M}$
such that each action admits a finite-trace fundamental domain. Such an
$\mathcal {M}$
is called a von Neumann coupling between
$\Gamma $
and
$\Lambda $
.
Definition 3.10 Two countable groups
$\Gamma $
and
$\Lambda $
are said to be vNOE, denoted
$\Gamma \sim _{\mathrm {vNOE}}\Lambda ,$
if there exists a von Neumann coupling between
$\Gamma $
and
$\Lambda $
with a common fundamental domain.
Theorem 3.11 For countable discrete groups
$\Gamma $
and
$\Lambda $
,
$\Gamma \sim _{\mathrm {vNOE}}\Lambda $
if and only if
$L\Gamma \sim _{\mathrm {vNOE}}L\Lambda $
.
Proof First, suppose that
$L\Gamma \sim _{\mathrm {vNOE}}L\Lambda $
, and let
$(\mathcal H,Q,\xi )$
be a triple as in condition (1) of Theorem 3.1. Set
$A=L\Gamma $
and
$B=L\Lambda $
, and consider
$\mathcal {M}=Q'\cap \mathcal {B}(\mathcal H)={_Q\mathcal {B}(\mathcal H)}$
. For
$\gamma \in \Gamma $
, let
$u_\gamma \in L\Gamma $
be the corresponding unitary and for
$T\in \mathcal {B}(\mathcal H)$
, define
$\sigma _\gamma (T)=u_\gamma T u_\gamma ^*$
. Since
$L\Gamma $
- and Q-actions on
$\mathcal H$
commute, it follows that
$\mathcal {M}$
is invariant under
$\sigma _\gamma $
for each
$\gamma \in \Gamma $
, and thus we have an action
$\Gamma {\, \curvearrowright \,}^\sigma \mathcal {M}$
. Similarly, since
$\mathcal H$
is a
$Q-B$
-bimodule, we have an action
$\Lambda {\, \curvearrowright \,}^\alpha \mathcal {M}$
given by
$\alpha _s(T)=v_s^*Tv_s, s\in \Lambda , T\in \mathcal {M}$
, where
$v_s\in L\Lambda $
is the unitary corresponding to
$s\in \Lambda $
. It is clear that the actions
$\Gamma {\, \curvearrowright \,}^\sigma \mathcal {M}$
and
$\Lambda {\, \curvearrowright \,}^\alpha \mathcal {M}$
commute. Let
$\mathrm {Tr}$
be the canonical trace on
$\mathcal {M}$
given by Proposition 2.4. Since
$L\Gamma $
- and Q-actions on
$\mathcal H$
commute, we have that for every
$\gamma \in \Gamma $
,
$u_\gamma $
is a Q-linear operator on
$\mathcal H$
and hence belongs to
$\mathcal {M}$
. Therefore, it now follows from the tracial property that
$\mathrm {Tr}(\sigma _\gamma (T))=\mathrm {Tr}(u_\gamma Tu_\gamma ^*)=\mathrm {Tr}(T)$
for all
$\gamma \in \Gamma , T\in \mathcal {M,}$
and hence
$\Gamma {\, \curvearrowright \,}^\sigma \mathcal {M}$
is trace-preserving. Similarly,
$\Lambda {\, \curvearrowright \,}^\alpha \mathcal {M}$
too is trace-preserving.
Let
$P\in \mathcal {B}(\mathcal H)$
be the orthogonal projection from
$\mathcal H$
onto
$\overline {\operatorname {Span}(Q\xi )}$
. It is straightforward to see that P is Q-linear and thus,
$P\in \mathcal {M}$
. Moreover, it follows from Remark 2.5 that
$\mathrm {Tr}(P)=1$
. Therefore, it only remains to show that P is a fundamental domain for both
$\Gamma $
- and
$\Lambda $
-actions. To see that P is a
$\Gamma $
-fundamental domain, we first note that, since
$\xi $
is tracial for the
$A\, \overline {\otimes }\, Q$
-module structure, we have, for
$a\in A, x\in Q$
, that
$$ \begin{align*} P((a\otimes x)\xi)=\tau_A(a)x\xi. \end{align*} $$
Furthermore, if
$a=\sum _{\gamma \in \Gamma }a_\gamma u_\gamma $
is the Fourier series expansion of
$a\in A$
, then we recall that
$\tau _A(a)=a_e$
, and thus
$P((a\otimes x)\xi )=a_e x\xi $
. Therefore,
$$ \begin{align*} \sigma_\gamma(P)((a\otimes x)\xi)&=u_\gamma Pu_\gamma^*((a\otimes x)\xi)\\ &=u_\gamma P\left(\left(\sum_{g\in\Gamma}a_gu_{\gamma^{-1}g}\otimes x\right)\xi\right)\\ &=a_\gamma(u_\gamma\otimes x)\xi. \end{align*} $$
If we let
$P_\gamma $
be the orthogonal projection from
$\mathcal H$
onto
$u_\gamma (\overline {\operatorname {Span}(Q\xi )})$
, then it follows from the above calculation that
$\sigma _\gamma (P)=P_\gamma $
, and it is straightforward to check that the projections
$\{P_\gamma \}_{\gamma \in \Gamma }$
are pairwise orthogonal. Moreover, since
$\mathcal H=\overline {\operatorname {Span}(A\, \overline {\otimes }\, Q)\xi }$
, we also get that
$\sum _{\gamma \in \Gamma }\sigma _\gamma (P)=1$
and hence P is a
$\Gamma $
-fundamental domain. Since we also have that
$\xi $
is bi-tracial for the
$Q-B$
-bimodule structure, we observe that, for
$b\in B, x\in Q$
,
$$ \begin{align*} P(x\xi b)=\tau_B(b)x\xi. \end{align*} $$
If
$b=\sum _{t\in \Lambda }b_tv_t$
is the Fourier series expansion of
$b\in B$
, then
$\tau _B(b)=b_e$
, and hence
$P(x\xi b)=b_ex\xi $
. For
$s\in \Lambda $
, let
$P_s$
be the orthogonal projection from
$\mathcal H$
onto
$(\overline {\operatorname {Span}(Q\xi )})v_s$
. Now, the following calculation shows that
$\alpha _s(P)=P_s$
, so,
$\{\alpha _s(P)\}_{s\in \Lambda }$
are pairwise orthogonal, and thus P is a
$\Lambda $
-fundamental domain since
$\mathcal H=\overline {\operatorname {Span}(Q\xi B)}$
.
$$ \begin{align*} \alpha_s(P)(x\xi b)&=v_s^*Pv_s\left(x\xi\sum_{t\in\Lambda}b_tv_t\right)\\ &=v_s^*(b_{s^{-1}}x\xi)\\ &=b_{s^{-1}}x\xi v_{s^{-1}}. \end{align*} $$
Conversely, suppose
$\Gamma \sim _{\mathrm {vNOE}}\Lambda $
, and let
$(\mathcal {M},\mathrm {Tr})$
be a von Neumann coupling between
$\Gamma $
and
$\Lambda $
with common fundamental domain
$p\in \mathcal {M}$
for both
$\Gamma {\, \curvearrowright \,}^\sigma \mathcal {M}$
and
$\Lambda {\, \curvearrowright \,}^\alpha \mathcal {M}$
. Let
$ A=L\Gamma , B=L\Lambda , \mathcal H=L^2(\mathcal {M},\mathrm {Tr})\, \overline {\otimes }\, \ell ^2(\Lambda ), Q=\mathcal {M}^{\Gamma }\rtimes \Lambda ,$
and
$\xi =p\otimes \delta _e$
. Let
$\tau $
be the trace on
$\mathcal {M}^\Gamma $
, which we recall is given by
$\tau (x)=\mathrm {Tr}(pxp)$
(see [Reference Ishan, Peterson and RuthIPR24, Proposition 4.2]). Consider the action of
$L\Gamma $
on
$\mathcal H$
given by
$$ \begin{align*}u_\gamma\eta=(\sigma_\gamma^0\otimes\operatorname{id})\eta, \qquad \gamma\in\Gamma,\eta\in\mathcal H,\end{align*} $$
where
$\sigma _\gamma ^0$
is the Koopman representation of
$\Gamma $
into
$\mathcal {U}(L^2(\mathcal {M},\mathrm {Tr}))$
. The action of
$\mathcal {M}^\Gamma $
on
$\mathcal H$
is given by
$$ \begin{align*}x\eta=(x\otimes\operatorname{id})\eta,\qquad x\in\mathcal{M}^\Gamma, \eta\in\mathcal H,\end{align*} $$
and
$\Lambda $
acts on
$\mathcal H$
on the left by
$$ \begin{align*}v_s\eta=(\alpha_s^0\otimes\lambda_\Lambda(s))\eta, \qquad s\in\Lambda,\eta\in\mathcal H,\end{align*} $$
where
$\lambda _\Lambda :\Lambda \to \mathcal {U}(\ell ^2\Lambda )$
is the left regular representation, and
$\alpha _s^0:\Lambda \to \mathcal {U}(L^2(\mathcal {M},\mathrm {Tr}))$
is the Koopman representation implementing the
$\Lambda $
-action. Since the
$\Gamma $
- and
$\Lambda $
-actions on
$\mathcal {M}$
commute, the actions defined above make
$\mathcal H$
into a left
$L\Gamma \, \overline {\otimes }\,(\mathcal {M}^\Gamma \rtimes \Lambda )$
-module. Furthermore, for
$g\in \Gamma , s\in \Lambda ,$
and
$x\in \mathcal {M}^\Gamma $
, we have
$$ \begin{align*} \langle (u_g\otimes xv_s)\xi, \xi\rangle&=\langle (u_g\otimes xv_s)(p\otimes \delta_e), p\otimes \delta_e\rangle\\ &=\langle \sigma_g(x\alpha_s(p))\otimes\delta_{s},p\otimes \delta_e\rangle\\ &=\delta_{s,e}\mathrm{Tr}(x\sigma_g(p)p)\\ &=\delta_{s,e}\delta_{g,e}\mathrm{Tr}(pxp)\\ &=\delta_{s,e}\delta_{g,e}\tau(x)\\ &=\tau_A(u_g)\tau_Q(xv_s). \end{align*} $$
Thus, it follows that
$\xi $
is tracial for the left
$L\Gamma \, \overline {\otimes }\,(\mathcal {M}^\Gamma \rtimes \Lambda )$
-module structure. For a fixed
$s\in \Lambda $
, we have
$$ \begin{align*} &\overline{\operatorname{Span}\{ (u_g\otimes xv_s)\xi :g\in\Gamma, x\in\mathcal{M}^\Gamma\}}\\&\quad=\overline{\operatorname{Span}\{ \sigma_g(x\alpha_s(p))\otimes\delta_{s}:g\in\Gamma, x\in\mathcal{M}^\Gamma\}}\\ &\quad=\overline{\operatorname{Span}\{ x\alpha_s(\sigma_g(p))\otimes \delta_s:g\in\Gamma, x\in\mathcal{M}^\Gamma\}}\\ &\quad=\overline{\operatorname{Span}\{ \alpha_s(\alpha_{s^{-1}}(x)\sigma_g(p))\otimes \delta_s:g\in\Gamma, x\in\mathcal{M}^\Gamma\}}\\ &\quad=\overline{\operatorname{Span}\{ \alpha_s(y\sigma_g(p))\otimes \delta_s: g\in\Gamma, y\in \mathcal{M}^\Gamma\}}\\ &\quad=(\alpha_s^0\otimes\lambda_\Lambda(s))(\overline{\operatorname{Span}\{y\sigma_g(p)\otimes\delta_e:g\in\Gamma,y\in\mathcal{M}^\Gamma\}})\\ &\quad=L^2(\mathcal{M},\mathrm{Tr})\, \overline{\otimes}\,\mathbb C\delta_s, \end{align*} $$
where the last equality follows from the fact that
$\overline {\operatorname {Span} \{x\sigma _g(p): g\in \Gamma , x \in \mathcal {M}^{\Gamma }\}}=L^2(\mathcal {M},\mathrm {Tr})$
[Reference Ishan, Peterson and RuthIPR24, Proposition 4.2]. Therefore, we have
$$ \begin{align*} \overline{\operatorname{Span}((A\, \overline{\otimes}\, Q)\xi)}&=\overline{\operatorname{Span}\{ (u_g\otimes xv_s)\xi :g\in\Gamma, x\in\mathcal{M}^\Gamma, s\in\Lambda\}}\\ &=\overline{\operatorname{Span}(L^2(\mathcal{M},\mathrm{Tr})\, \overline{\otimes}\,\mathbb C\delta_s:s\in\Lambda)}=\mathcal H. \end{align*} $$
Finally, the right action of
$L\Lambda $
on
$\mathcal H$
given by
$$ \begin{align*} \eta v_s=(\operatorname{id}\otimes\rho_\Lambda(s^{-1}))\eta,\qquad s\in\Lambda, \eta\in\mathcal H, \end{align*} $$
where
$\rho _\Lambda :\Lambda \to \mathcal {U}(\ell ^2\Lambda )$
is the right regular representation, makes
$\mathcal H$
into a
$Q-L\Lambda $
-bimodule. For
$x\in \mathcal {M}^\Gamma $
and
$s,t\in \Lambda $
, we have
$$ \begin{align*} \langle xv_s(p\otimes \delta_e)v_t,p\otimes\delta_e\rangle=\langle x\alpha_s(p)\otimes\delta_{st},p\otimes\delta_e\rangle=\delta_{s,e}\delta_{t,e}\mathrm{Tr}(pxp)=\tau_Q(xv_s)\tau_B(v_t), \end{align*} $$
and hence,
$\xi $
is a tracial vector for the
$Q-B$
-bimodule structure. We recall from the proof of [Reference Ishan, Peterson and RuthIPR24, Proposition 4.2], that, since p is
$\Lambda $
-fundamental domain, we have a direct sum decomposition
$L^2(\mathcal {M},\mathrm {Tr})=\sum _{s\in \Lambda }L^2(\mathcal {M},\mathrm {Tr})\alpha _s(p)$
. Thus, to show that
$\overline {\operatorname {Span}(Q\xi B)}=\mathcal H$
, it suffices to show that, for
$s\in \Lambda $
,
$\overline {\operatorname {Span}\{xv_s\xi v_t:x\in \mathcal {M}^\Gamma ,t\in \Lambda \}}=L^2(\mathcal {M},\mathrm {Tr})\alpha _s(p)\, \overline {\otimes }\,\ell ^2\Lambda $
. To this end, fix
$s\in \Lambda $
and note that
$$ \begin{align*} \overline{\operatorname{Span}\{xv_s(p\otimes\delta_e)v_t:x\in\mathcal{M}^\Gamma,t\in\Lambda\}}&=\overline{\operatorname{Span}\{\alpha_s(\alpha_{s^{-1}}(x)p)\otimes\delta_{st}: x\in\mathcal{M}^\Gamma,t\in\Lambda\}}\\ &=(\alpha_s^0\otimes\lambda_\Lambda(s))(\overline{\operatorname{Span}\{yp\otimes\delta_t:y\in\mathcal{M}^\Gamma,t\in\Lambda\}})\\ &=(\alpha_s^0\otimes\lambda_\Lambda(s))(L^2(\mathcal{M},\mathrm{Tr})p\, \overline{\otimes}\,\ell^2\Lambda)\\ &=L^2(\mathcal{M},\mathrm{Tr})\alpha_s(p)\, \overline{\otimes}\,\ell^2\Lambda. \end{align*} $$
3.3 Relationship to von Neumann equivalence
Definition 3.12 [Reference Ishan, Peterson and RuthIPR24]
Let A and B be tracial von Neumann algebras and let
$\mathcal {M}$
be a semi-finite von Neumann algebra such that
$A\subset \mathcal {M}$
and
$B^{\mathrm {op}}\subset \mathcal {M}$
.
-
(1) A fundamental domain for A inside of
$\mathcal M$
consists of a realization of the standard representation
$A \subset \mathcal B(L^2(A))$
as an intermediate von Neumann subalgebra
$A \subset \mathcal B(L^2(A)) \subset \mathcal M$
. The fundamental domain is finite if finite-rank projections in
$\mathcal B(L^2(A))$
are mapped to finite projections in
$\mathcal M$
. -
(2)
$\mathcal {M}$
is a von Neumann coupling between A and B if
$B^{\mathrm {op}} \subset A' \cap \mathcal M$
and each inclusion
$A \subset \mathcal M$
and
$B^{\mathrm {op}} \subset \mathcal M$
has a finite fundamental domain.
Definition 3.13 [Reference Ishan, Peterson and RuthIPR24]
Two tracial von Neumann algebras A and B are vNE, denoted
$A \sim _{\mathrm {vNE}} B$
, if there exists a von Neumann coupling between them.
Proposition 3.14 Let
$(A,\tau _A)$
and
$(B,\tau _B)$
be tracial von Neumann algebras. If
$A\sim _{\mathrm {vNOE}} B$
, then
$A\sim _{\mathrm {vNE}}B$
.
Proof Suppose
$(\mathcal H,Q,\xi )$
is a triple as in condition (1) of Theorem 3.1. As in the proof of (1) implies (2) in Theorem 3.1, let
$U:\mathcal H\to L^2(A\, \overline {\otimes }\, Q)$
be the unitary such that
$U(x\xi )=\hat x$
for all
$x\in A\, \overline {\otimes }\, Q$
, and let
$\phi :B\to A\, \overline {\otimes }\, Q$
be the
$*$
-homomorphism obtained therein. Let
$\mathcal {M}=Q'\cap \mathcal {B}(\mathcal H)=\mathcal {B}(L^2(A))\, \overline {\otimes }\, Q^{\mathrm {op}}$
. We will show that
$\mathcal {M}$
is a von Neumann coupling between A and B. It is clear that the inclusion
$A\subset \mathcal {M}$
has a finite fundamental domain. We recall that the argument used in defining
$\phi $
shows that we have an inclusion
$B^{\mathrm {op}}\subset \mathcal {M}$
and moreover, since the left A- and right B-actions on
$\mathcal H$
commute, we have that
$B^{\mathrm {op}}\subset A'\cap \mathcal {M}$
. Thus, it only remains to show that the inclusion
$B^{\mathrm {op}}\subset \mathcal {M}$
has a finite fundamental domain. To this end, note that we can also view
$\mathcal H$
as an
$A-B\, \overline {\otimes }\, Q^{\mathrm {op}}$
-bimodule, and
$\xi $
is tracial and cyclic for the right
$B\, \overline {\otimes }\, Q^{\mathrm {op}}$
-module structure. Thus, by the same construction as above, we get an inclusion
$B^{\mathrm {op}}\subset {Q^{\mathrm {op}}}'\cap \mathcal {B}(\mathcal H)=\mathcal {B}(L^2(B))\, \overline {\otimes }\, Q$
. Since
$\mathcal {M}=Q'\cap \mathcal {B}(\mathcal H)={Q^{\mathrm {op}}}'\cap \mathcal {B}(\mathcal H)$
, we get that the inclusion
$B^{\mathrm {op}}\subset \mathcal {M}$
admits a finite fundamental domain and hence
$A\sim _{\mathrm {vNE}}B$
.
4 Toward an analog of Singer’s theorem
The main goal of this section is to prove the following theorem.
Theorem 4.1 If
$\Gamma $
and
$\Lambda $
are countable discrete groups such that
$\Gamma \sim _{\mathrm {vNOE}}\Lambda $
, then there exist tracial von Neumann algebras
$(A,\tau _A), (B,\tau _B)$
, trace-preserving actions
$\Gamma {\, \curvearrowright \,} A, \Lambda {\, \curvearrowright \,} B$
, and a trace-preserving isomorphism
$\theta :B\rtimes \Lambda \to A\rtimes \Gamma $
.
Before proving the theorem, we first set up some notations and recall a few facts. Let
$\Gamma $
be a countable discrete group and
$(M,\tau )$
be a tracial von Neumann algebra. A 1-cocycle for a trace-preserving action
$\Gamma {\, \curvearrowright \,}^\alpha (M,\tau )$
is a map
$w:\Gamma \to \mathcal {U}(M)$
that satisfies the following cocycle identity:
$$ \begin{align*} w_s\alpha_s(w_t)=w_{st}, \quad s,t\in\Gamma. \end{align*} $$
If
$\Gamma {\, \curvearrowright \,}^\beta (M,\tau )$
is another trace-preserving action, then we say that
$\alpha $
and
$\beta $
are cocycle conjugate if there exists an automorphism
$\theta \in \operatorname {Aut}(M,\tau )$
and a 1-cocycle
$w:\Gamma \to \mathcal {U}(M)$
for
$\alpha $
such that
$$ \begin{align} \theta\circ\beta_s\circ\theta^{-1}=\operatorname{Ad}(w_s)\circ\alpha_s,\quad s\in\Gamma. \end{align} $$
We recall that if
$\Gamma {\, \curvearrowright \,}^\alpha (M,\tau )$
and
$\Gamma {\, \curvearrowright \,}^\beta (M,\tau )$
are cocycle conjugate, then
$M\rtimes _\alpha \Gamma \cong M\rtimes _\beta \Gamma $
. Indeed, let
$\theta \in \operatorname {Aut}(M,\tau )$
and
$w:\Gamma \to \mathcal {U}(M)$
be as in (4.1), and consider the map
$\Theta :M\rtimes _\alpha \Gamma \to M\rtimes _\beta \Gamma $
given by
$$ \begin{align*} \Theta(xu_s)=\operatorname{Ad}(w_s)(\theta(x))v_s, \quad x\in M, s\in\Gamma, \end{align*} $$
where, for
$s\in \Gamma $
,
$u_s,v_s$
represent the canonical group unitaries in
$M\rtimes _\alpha \Gamma ,M\rtimes _\beta \Gamma $
, respectively. It is then straightforward to verify that
$\Theta $
is an isomorphism.
Proof of Theorem 4.1
Let
$\Gamma {\, \curvearrowright \,}^\sigma \mathcal {M}$
and
$\Lambda {\, \curvearrowright \,}^\alpha \mathcal {M}$
be commuting, trace-preserving actions of countable discrete groups
$\Gamma $
and
$\Lambda $
on a semi-finite von Neumann algebra
$\mathcal {M}$
with a faithful normal semi-finite trace
$\mathrm {Tr}$
. Let
$p\in \mathcal {M}$
be a finite-trace projection which is a common fundamental domain for both
$\Gamma $
- and
$\Lambda $
-actions, that is,
$\{\sigma _\gamma (p)\}_{\gamma \in \Gamma }$
are mutually orthogonal and
$\sum _{\gamma \in \Gamma }\sigma _\gamma (p)=1$
(SOT), and similarly,
$\{\alpha _\lambda (p)\}_{\lambda \in \Lambda }$
are mutually orthogonal and
$\sum _{\lambda \in \Lambda }\alpha _\lambda (p)=1$
(SOT). From [Reference Ishan, Peterson and RuthIPR24, Proposition 4.2], there exists a unitary
$\mathcal F_p:\ell ^2\Gamma \, \overline {\otimes }\, L^2(\mathcal {M}^\Gamma ,\tau )\to L^2(\mathcal {M},\mathrm {Tr})$
such that
$$ \begin{align*} \mathcal F_p(\delta_\gamma\otimes x)=\sigma_{\gamma^{-1}}(p)x\qquad \text{for all } \gamma\in\Gamma, x\in\mathcal{M}^\Gamma, \end{align*} $$
where the trace
$\tau $
on
$\mathcal {M}^\Gamma $
is given by
$\tau (x)=\mathrm {Tr}(pxp),~x\in \mathcal {M}^\Gamma $
.Footnote
1
Furthermore, from [Reference Ishan, Peterson and RuthIPR24, Proposition 4.3], there is a trace-preserving isomorphism
$\Delta _p^\Gamma :\mathcal {M}\rtimes \Gamma \to \mathcal {B}(\ell ^2\Gamma )\, \overline {\otimes }\,\mathcal {M}^\Gamma $
such that for
$\gamma \in \Gamma $
and
$x\in \mathcal {M}$
,
$$ \begin{align*} \Delta_p^\Gamma(u_\gamma)=\rho_\gamma\otimes 1,\qquad \Delta_p^\Gamma(x)=\mathcal F_p^*x\mathcal F_p. \end{align*} $$
If we view
$\mathcal {B}(\ell ^2\Gamma )\, \overline {\otimes }\,\mathcal {M}^\Gamma $
as
$\mathcal {M}^\Gamma $
-valued
$\Gamma \times \Gamma $
matrices, then we have that for all
$x\in \mathcal {M}$
,
$\Delta _p^\Gamma (x)=[x_{s,t}]_{s,t}$
, where
$$ \begin{align*} x_{s,t}=\sum_{\gamma\in\Gamma}\sigma_\gamma(\sigma_{t^{-1}}(p)x\sigma_{s^{-1}}(p))\in\mathcal{M}^\Gamma.\\[-42pt] \end{align*} $$
Since the actions of
$\Gamma $
and
$\Lambda $
on
$\mathcal {M}$
commute, we get a well-defined action of
$\Lambda $
on
$\mathcal {M}\rtimes \Gamma $
, which we denote by
$\alpha \rtimes \operatorname {id}_\Gamma $
, and it is given by
$$ \begin{align*} (\alpha_\lambda\rtimes\operatorname{id}_\Gamma)(xu_\gamma)=\alpha_\lambda(x)u_\gamma, \quad\lambda\in\Lambda,\gamma\in\Gamma,x\in\mathcal{M}. \end{align*} $$
Further, let
$\operatorname {id}\otimes \alpha $
be the action of
$\Lambda $
on
$\mathcal {B}(\ell ^2\Gamma )\, \overline {\otimes }\,\mathcal {M}^\Gamma $
given by
$$ \begin{align*} (\operatorname{id}\otimes\alpha_\lambda)(T\otimes x)=T\otimes\alpha_\lambda(x), \quad \lambda\in\Lambda,T\in\mathcal{B}(\ell^2\Gamma), x\in\mathcal{M}^\Gamma. \end{align*} $$
Define an action
$\tilde {\alpha }$
of
$\Lambda $
on
$\mathcal {B}(\ell ^2\Gamma )\, \overline {\otimes }\,\mathcal {M}^\Gamma $
by
$$ \begin{align*} \tilde{\alpha}_\lambda=\Delta_p^\Gamma\circ(\alpha_\lambda\rtimes\operatorname{id}_\Gamma)\circ(\Delta_p^\Gamma)^{-1},~\lambda\in\Lambda. \end{align*} $$
By definition,
$\tilde {\alpha }$
is conjugate to
$\alpha \rtimes \operatorname {id}_\Gamma $
, and hence we get an isomorphism of the crossed products
$$ \begin{align*} \mathcal{M}\rtimes(\Gamma\times\Lambda)=(\mathcal{M}\rtimes\Gamma)\rtimes_{\alpha\rtimes\operatorname{id}_\Gamma}\Lambda\underset{\cong}{\overset{\Delta_p^\Gamma\rtimes\operatorname{id}_\Gamma}{\longrightarrow}}(\mathcal{B}(\ell^2\Gamma)\, \overline{\otimes}\,\mathcal{M}^\Gamma)\rtimes_{\tilde{\alpha}}\Lambda. \end{align*} $$
Now, we note that for any
$\lambda \in \Lambda $
,
$\alpha _{\lambda ^{-1}}(p)$
is again a
$\Gamma $
-fundamental domain and hence we can consider the map
$\Delta _{\alpha _{\lambda ^{-1}}(p)}^\Gamma :\mathcal {M}\rtimes \Gamma \to \mathcal {B}(\ell ^2)\otimes \mathcal {M}^\Gamma $
defined analogously to
$\Delta _p^\Gamma $
. For any
$x\in \mathcal {M}$
and
$s,t\in \Gamma $
, by a slight abuse of notation, let
$[\Delta _p^\Gamma (x)]_{s,t}$
be the
$(s,t)$
-entry in the matrix representation of
$\Delta _p^\Gamma (x)$
. Similarly, consider
$[\Delta _{\alpha _{\lambda ^{-1}}(p)}^\Gamma (x)]_{s,t}$
. We observe that
$$ \begin{align*} \alpha_\lambda([\Delta_{\alpha_{\lambda^{-1}}(p)}^\Gamma(x)]_{s,t})&=\alpha_\lambda\left(\sum_{\gamma\in\Gamma}\sigma_\gamma(\sigma_{t^{-1}}(\alpha_{\lambda^{-1}}(p))x\sigma_{s^{-1}}(\alpha_{\lambda^{-1}}(p)))\right)\\ &=\sum_{\gamma\in\Gamma}\sigma_\gamma(\sigma_{t^{-1}}(p)\alpha_\lambda(x)\sigma_{s^{-1}}(p))\\ &=[\Delta_p^\Gamma(\alpha_\lambda(x))]_{s,t}, \end{align*} $$
whence it follows that
$\Delta _p^\Gamma (\alpha _\lambda (x))=(\operatorname {id}\otimes \alpha _\lambda )(\Delta _{\alpha _{\lambda ^{-1}}(p)}^\Gamma (x))$
for all
$x\in \mathcal {M}$
and
$\lambda \in \Lambda $
. Therefore, for any
$x\in \mathcal {M}, \gamma \in \Gamma $
, and
$\lambda \in \Lambda $
, we have
$$ \begin{align*} (\Delta_p^\Gamma\circ(\alpha_\lambda\rtimes\operatorname{id}_\Gamma))(xu_\gamma)&=\Delta_p^\Gamma(\alpha_\lambda(x)u_\gamma)\\ &=\Delta_p^\Gamma(\alpha_\lambda(x))\Delta_p^\Gamma(u_\gamma)\\ &=(\operatorname{id}\otimes\alpha_\lambda)(\Delta_{\alpha_{\lambda^{-1}}(p)}^\Gamma(x))(\rho_\gamma\otimes 1)\\ &=(\operatorname{id}\otimes\alpha_\lambda)(\mathcal F_{\alpha_{\lambda^{-1}}(p)}^*\mathcal F_p\mathcal F_p^*x\mathcal F_p\mathcal F_p^*\mathcal F_{\alpha_{\lambda^{-1}}(p)})(\rho_\gamma\otimes 1)\\ &=(\operatorname{id}\otimes\alpha_\lambda)(v_\lambda\Delta_p^\Gamma(x)v_\lambda^*)(\rho_\gamma\otimes 1)\\ &=(\operatorname{id}\otimes\alpha_\lambda)(v_\lambda\Delta_p^\Gamma(xu_\gamma)v_\lambda^*), \end{align*} $$
where
$v_\lambda =\mathcal F^*_{\alpha _{\lambda ^{-1}}(p)}\mathcal F_p$
. The last equality follows from the fact that
$v_\lambda \in \mathcal {U}(L\Gamma \, \overline {\otimes }\,\mathcal {M}^\Gamma )$
(see [Reference Ishan, Peterson and RuthIPR24, Proposition 4.4]), and hence commutes with
$\rho _\gamma \otimes 1$
. Therefore, if we let
$w_\lambda =(\operatorname {id}\otimes \alpha _\lambda )(v_\lambda )\in \mathcal {U}(L\Gamma \, \overline {\otimes }\,\mathcal {M}^\Gamma )$
, then we have that
$$ \begin{align*} \tilde{\alpha}_\lambda=\Delta_p^\Gamma\circ(\alpha_\lambda\rtimes\operatorname{id}_\Gamma)\circ(\Delta_p^\Gamma)^{-1}=\operatorname{Ad}(w_\lambda)\circ(\operatorname{id}\otimes\alpha_\lambda). \end{align*} $$
Claim The map
$w:\Lambda \to \mathcal {U}(L\Gamma \, \overline {\otimes }\,\mathcal {M}^\Gamma )$
defined by
$w_\lambda =(\operatorname {id}\otimes \alpha _\lambda )(v_\lambda )$
is a 1-cocycle for
$\Lambda {\, \curvearrowright \,}^{\operatorname {id}\otimes \alpha }\mathcal {B}(\ell ^2\Gamma )\, \overline {\otimes }\,\mathcal {M}^\Gamma .$
Proof of Claim
First note that, for any
$y\in \mathfrak {n}_{\mathrm {Tr}}\subset \mathcal {M}$
, it is straightforward to verify that
$$ \begin{align*} \mathcal F_p^*(y)=\sum_{\gamma\in\Gamma}\delta_\gamma\otimes y_\gamma, \end{align*} $$
where
$$ \begin{align*} y_\gamma=\sum_{b\in\Gamma}\sigma_{b\gamma^{-1}}(p)\sigma_b(y). \end{align*} $$
Since
$\mathrm {Tr}(p)<\infty $
, so, for any
$a\in \Gamma $
and
$x\in \mathcal {M}^\Gamma $
, we have that
$\mathrm {Tr}(\sigma _{a^{-1}}(p)x)<\infty $
and hence
$\sigma _{a^{-1}}(p)x\in \mathfrak {n}_{\mathrm {Tr}}$
. Therefore, for any
$a\in \Gamma $
and
$x\in \mathcal {M}^\Gamma $
, we have
$$ \begin{align*} \mathcal F^*_{\alpha_{\lambda^{-1}}(p)}\mathcal F_p(\delta_a\otimes x)&=\mathcal F^*_{\alpha_{\lambda^{-1}}(p)}(\sigma_{a^{-1}}(p)x)\\ &=\sum_{\gamma\in\Gamma}\delta_\gamma\otimes\left(\sum_{b\in\Gamma}\sigma_{b\gamma^{-1}}(\alpha_{\lambda^{-1}}(p))\sigma_b(\sigma_{a^{-1}}(p)x)\right)\\ &=\sum_{\gamma\in\Gamma}\delta_\gamma\otimes\left(\sum_{b\in\Gamma}\sigma_{b\gamma^{-1}}(\alpha_{\lambda^{-1}}(p))\sigma_{ba^{-1}}(p)x\right). \end{align*} $$
Thus, as an
$\mathcal {M}^\Gamma $
-valued
$\Gamma \times \Gamma $
matrix, we can write
$v_\lambda =[[v_\lambda ]_{s,t}]_{s,t},$
where
$$ \begin{align*} [v_\lambda]_{s,t}=\sum_{\gamma\in\Gamma}\sigma_{\gamma s^{-1}}(\alpha_{\lambda^{-1}}(p))\sigma_{\gamma t^{-1}}(p), \end{align*} $$
and therefore,
$w_\lambda $
can be written as an
$\mathcal {M}^\Gamma $
-valued
$\Gamma \times \Gamma $
matrix
$w_\lambda =[[w_\lambda ]_{s,t}]_{s,t}$
, where
$$ \begin{align*} [w_\lambda]_{s,t}=\alpha_\lambda([v_\lambda]_{s,t})=\sum_{\gamma\in\Gamma}\sigma_{\gamma s^{-1}}(p)\sigma_{\gamma t^{-1}}(\alpha_\lambda(p)). \end{align*} $$
Finally, the following calculation verifies the cocycle identity for w. For
$\lambda _1,\lambda _2\in \Lambda $
, and
$s,t\in \Gamma $
, we have
$$ \begin{align*} &[w_{\lambda_1}(\operatorname{id}\otimes\alpha_{\lambda_1})(w_{\lambda_2})]_{s,t}\\ &\quad=\sum_{a\in\Gamma}[w_{\lambda_1}]_{s,a}[(\operatorname{id}\otimes\alpha_{\lambda_{1}})(w_{\lambda_2})]_{a,t}\\ &\quad=\sum_{a\in\Gamma}\left[\left(\sum_{\gamma\in\Gamma}\sigma_{\gamma s^{-1}}(p)\sigma_{\gamma a^{-1}}(\alpha_{\lambda_1}(p))\right)\left(\sum_{\gamma'\in\Gamma}\sigma_{\gamma' a^{-1}}(\alpha_{\lambda_{1}}(p))\sigma_{\gamma' t^{-1}}(\alpha_{\lambda_1\lambda_2}(p))\right)\right]\\&\quad=\sum_{a\in\Gamma}\sum_{\gamma\in\Gamma}\sigma_{\gamma s^{-1}}(p)\sigma_{\gamma a^{-1}}(\alpha_{\lambda_1}(p))\sigma_{\gamma t^{-1}}(\alpha_{\lambda_1\lambda_2}(p))\\ &\quad=\sum_{\gamma\in\Gamma}\sum_{a\in\Gamma}\sigma_{\gamma s^{-1}}(p)\sigma_{\gamma a^{-1}}(\alpha_{\lambda_1}(p))\sigma_{\gamma t^{-1}}(\alpha_{\lambda_1\lambda_2}(p))\\ &\quad=\sum_{\gamma\in\Gamma}\sigma_{\gamma s^{-1}}(p)\sigma_{\gamma t^{-1}}(\alpha_{\lambda_1\lambda_2}(p))\\ &\quad=[w_{\lambda_1\lambda_2}]_{s,t}. \\[-36pt]\end{align*} $$
It now follows from the above claim that the actions
$\tilde {\alpha }$
and
$\operatorname {id}\otimes \alpha $
of
$\Lambda $
on
$\mathcal {B}(\ell ^2\Gamma )\, \overline {\otimes }\,\mathcal {M}^\Gamma $
are cocycle conjugate, and hence we get the following isomorphisms of the crossed products:
$$ \begin{align*} (\mathcal{B}(\ell^2\Gamma)\, \overline{\otimes}\,\mathcal{M}^\Gamma)\rtimes_{\tilde{\alpha}}\Lambda\underset{\cong}{\overset{\Psi^\Gamma}{\longrightarrow}} (\mathcal{B}(\ell^2\Gamma)\, \overline{\otimes}\,\mathcal{M}^\Gamma)\rtimes_{\operatorname{id}\otimes\alpha}\Lambda \underset{\cong}{\overset{\Psi^\alpha}{\longrightarrow}} \mathcal{B}(\ell^2\Gamma)\, \overline{\otimes}\,(\mathcal{M}^\Gamma\rtimes_\alpha\Lambda), \end{align*} $$
where the isomorphism
$\Psi ^\alpha $
is the canonical isomorphism and satisfies
$$ \begin{align*} \Psi^\alpha((T\otimes x)u_\lambda)=T\otimes xu_\lambda, \qquad T\in\mathcal{B}(\ell^2\Gamma), x\in\mathcal{M}^\Gamma, \lambda\in\Lambda. \end{align*} $$
Similarly, starting with the isomorphism
$\Delta _p^\Lambda :\mathcal {M}\rtimes \Lambda \to \mathcal {B}(\ell ^2\Lambda )\, \overline {\otimes }\,\mathcal {M}^\Lambda $
, and performing the above analysis, yields the following isomorphisms of the crossed products:
$$ \begin{align*} \mathcal{M}\rtimes(\Gamma\times\Lambda)=(\mathcal{M}\rtimes\Lambda)\rtimes_{\sigma\rtimes\operatorname{id}_\Lambda}\Gamma\underset{\cong}{\overset{\Delta_p^\Lambda\rtimes\operatorname{id}_\Lambda}{\longrightarrow}}(\mathcal{B}(\ell^2\Lambda)\, \overline{\otimes}\,\mathcal{M}^\Lambda)\rtimes_{\tilde{\sigma}}\Gamma, \end{align*} $$
$$ \begin{align*} (\mathcal{B}(\ell^2\Lambda)\, \overline{\otimes}\,\mathcal{M}^\Lambda)\rtimes_{\tilde{\sigma}}\Gamma\underset{\cong}{\overset{\Psi^\Lambda}{\longrightarrow}} (\mathcal{B}(\ell^2\Lambda)\, \overline{\otimes}\,\mathcal{M}^\Lambda)\rtimes_{\operatorname{id}\otimes\sigma}\Gamma\underset{\cong}{\overset{\Psi^\sigma}{\longrightarrow}} \mathcal{B}(\ell^2\Lambda)\, \overline{\otimes}\,(\mathcal{M}^\Lambda\rtimes_{\sigma}\Gamma). \end{align*} $$
Thus, if
$\Phi :\mathcal {B}(\ell ^2\Gamma )\, \overline {\otimes }\,(\mathcal {M}^\Gamma \rtimes _\alpha \Lambda )\to \mathcal {B}(\ell ^2\Lambda )\, \overline {\otimes }\,(\mathcal {M}^\Lambda \rtimes _\sigma \Gamma )$
is given by
$$ \begin{align*} \Phi:=\Psi^\sigma\circ\Psi^\Lambda\circ\theta\circ(\Psi^\Gamma)^{-1}\circ(\Psi^\alpha)^{-1}, \end{align*} $$
where
$\theta :=\Delta _p^\Lambda \rtimes \operatorname {id}_\Lambda \circ (\Delta _p^\Gamma \rtimes \operatorname {id}_\Gamma )^{-1}$
, then
$\Phi $
is an isomorphism and moreover, the following diagram commutes:
Let
$\omega _{e_\Gamma ,e_\Gamma }\in \mathcal {B}(\ell ^2\Gamma )$
(resp.,
$\omega _{e_\Lambda ,e_\Lambda }\in \mathcal {B}(\ell ^2\Lambda )$
) denote the orthogonal projection onto
$\mathbb {C}\delta _{e_\Gamma }$
(resp.,
$\mathbb {C}\delta _{e_\Lambda }$
). We make the following observations:
-
•
$\Psi ^\alpha (\omega _{e_\Gamma ,e_\Gamma }\otimes 1)=\omega _{e_\Gamma ,e_\Gamma }\otimes 1$
and
$\Psi ^\sigma (\omega _{e_\Lambda ,e_\Lambda }\otimes 1)=\omega _{e_\Lambda ,e_\Lambda }\otimes 1$
. -
•
$\Psi ^\Gamma (x)=x$
for all
$x\in \mathcal {B}(\ell ^2\Gamma )\, \overline {\otimes }\,\mathcal {M}^\Gamma $
. This is true because of how
$\tilde {\alpha }$
and
$\operatorname {id}\otimes \alpha $
are cocycle conjugate. Similarly,
$\Psi ^\Lambda (y)=y$
for all
$y\in \mathcal {B}(\ell ^2\Lambda )\, \overline {\otimes }\,\mathcal {M}^\Lambda $
. -
•
$\Delta _p^\Gamma (p)=\omega _{e_\Gamma ,e_\Gamma }\otimes 1$
,
$\Delta _p^\Lambda (p)=\omega _{e_\Lambda ,e_\Lambda }\otimes 1$
,
$(\Delta _p^\Gamma \rtimes \operatorname {id}_\Gamma )(p)=\omega _{e_\Gamma ,e_\Gamma }\otimes 1$
, and
$(\Delta _p^\Lambda \rtimes \operatorname {id}_\Lambda )(p)=\omega _{e_\Lambda ,e_\Lambda }\otimes 1$
. These in particular imply that
$$ \begin{align*} \theta(\omega_{e_\Gamma,e_\Gamma}\otimes 1)=\Delta_p^\Lambda\rtimes\operatorname{id}_\Lambda((\Delta_p^\Gamma\rtimes\operatorname{id}_\Gamma)^{-1}(\omega_{e_\Gamma,e_\Gamma}\otimes 1))=\Delta_p^\Lambda\rtimes\operatorname{id}_{\Lambda}(p)=\omega_{e_\Lambda,e_\Lambda}\otimes 1. \end{align*} $$
From the observations above, we obtain that
$$ \begin{align*} \Phi(\omega_{e_\Gamma,e_\Gamma}\otimes 1)&=\Psi^\sigma(\Psi^\Lambda(\theta((\Psi^\Gamma)^{-1}((\Psi^\alpha)^{-1}(\omega_{e_\Gamma,e_\Gamma}\otimes 1)))))\\ &=\Psi^\sigma(\Psi^\Lambda(\theta(\omega_{e_\Gamma,e_\Gamma}\otimes 1)))\\ &=\Psi^\sigma(\Psi^\Lambda(\omega_{e_\Lambda,e_\Lambda}\otimes 1))\\ &=\omega_{e_\Lambda,e_\Lambda}\otimes 1. \end{align*} $$
Therefore, we have
$$ \begin{align*} \Phi(\mathcal{M}^{\Gamma}\rtimes_\alpha \Lambda)&=\Phi((\omega_{e_\Gamma,e_\Gamma}\otimes 1)(\mathcal{B}(\ell^2\Gamma)\, \overline{\otimes}\, (\mathcal{M}^{\Gamma}\rtimes_\alpha \Lambda))(\omega_{e_\Gamma,e_\Gamma}\otimes 1))\\ &=(\omega_{e_\Lambda,e_\Lambda}\otimes 1)(\mathcal{B}(\ell^2\Lambda)\, \overline{\otimes}\, (\mathcal{M}^{\Lambda}\rtimes_\sigma \Gamma))(\omega_{e_\Lambda,e_\Lambda}\otimes 1)\\ &=\mathcal{M}^{\Lambda}\rtimes_\sigma \Gamma. \end{align*} $$
$\blacksquare $
Acknowledgements
The authors would like to express deep gratitude to Ben Hayes for his valuable insights, continuous support, and constant encouragement throughout this project. This work has benefited profoundly from discussions with Ben Hayes on numerous occasions and from his encouraging them to look into [Reference Berendschot and VaesBV25]. The project began with the authors’ meeting at the “NCGOA Spring Institute 2023” held at Vanderbilt University, and the authors thank the organizers of the conference for the opportunity. Finally, the authors would like to thank the anonymous referee for helpful suggestions and pointing out an argument to them that helped in simplifying the proof of Theorem 1.7 and extending it to the case of an arbitrary countably infinite graph product.
Open access
